Masuri ale imprastierii sau variabilitatii - Biostatistica

Masuri ale imprastierii sau variabilitatii - Biostatistica

Masurile valorii centrale nu ne dau nici o indicatie privind imprastierea sau variabilitatea intr-un set de observatii.

Exemplu: Sa consideram ca avem doua comunitati A si B; media valorii luata in studiu in cele doua comunitati este aceeasi, insa distributiile valorilor (imprastierea acestora) este diferita (conform tabelului 8.5).

Tabelul 8.5: Locuitorii din doua comunitati A si B

Pentru a se putea caracteriza gradul de imprastiere ale valorilor unei serii de valori, se defineste o marime speciala, numita deviatie standard.

O alta masura utila de caracterizare a imprastierii este rangul, definit ca diferenta intre cea mai mica si cea mai mare valoare a seriei.

Varianta (dispersia) si deviatia standard:

Varianta este media patratelor deviatiilor (abaterilor) de la medie. Cand calculam varianta unei serii statistice, suma patratelor deviatiilor de la medie se imparte la (n - 1), deoarece aceasta da o mai buna estimare a variantei populatiei totale. Numitorul (n - 1) este numit numarul gradelor de libertate a variantei.

Formula de calcul a variantei pentru o serie de valori x₁ , x₂ , . , x_n va fi:

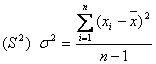
Exemplu: Valorile variatiei intr-un set de rezultate sunt prezentate in tabelul 8.6.

Tabelul 8.6: Varianta intr-un set de rezultate

Numarul de grade de libertate: 11-1=10.

Mediana: 52.

Modulul: 48.

Definitie:

Radacina patrata a variantei se numeste deviatie standard.

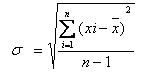
Eroarea standard (e.s.) este data de formula:

Pentru exemplul nostru (tabelul 8.6):