Teste statistice pentru analiza dispersiei si a mediei - Biostatistica

Teste statistice pentru analiza dispersiei si a mediei - Biostatistica

1. Compararea a doua dispersii

Notam raportul F_1,2 al dispersiilor s si s

Acest raport, in care se convine sa se puna la numarator dispersia cea mai mare, traduce divergenta intre doua dispersii si va fi folosit pentru a testa semnificatia.

Daca, intr-adevar, esantioanele sunt extrase din aceeasi populatie de origine, dispersiile s si s reprezinta o estimare a dispersiei S² a acestei populatii. Teoretic, ar trebui sa fie verificata relatia: s s si prin urmare F_1,2 = 1.

Uneori fluctuatiile fortuite nu sunt raspunzatoare de marirea raportului decat pana la o valoare limita, valoare pe care o putem calcula, si care variaza evident cu marimea esantionului. Atunci cand raportul F depaseste aceasta valoare limita, divergenta este prea importanta pentru a fi atribuita numai fluctuatiei de esantionaj pe care hazardul o poate determina in interiorul unei populatii unice. Aceasta ipoteza trebuie deci eliminata si divergenta trebuie considerata semnificativa.

Sndcor a stabilit tabelele raportului F care ne permit sa rezolvam problema din punct de vedere practic. Aceste tabele dau direct, pentru coeficientii de securitate obisnuiti, 95% si 99% si in functie de marimile esantioanelor n₁ si n₂ (mai precis, in functie de numarul gradelor de libertate g = n₁ - 1 si g = n₂ - 1 ale fiecarui esantion) valorile limita ale lui F sub care se poate considera ca dispersiile studiate difera semnificativ. Este suficient sa formam raportul celor doua dispersii, , si sa cercetam daca este superior valorii limita data de tabel.

Exemplu:

Dupa administrarea unui somnifer intr-un grup de 11 subiecti, se observa un timp mediu de somn de 10.6 h, cu o abatere standard de 2.3 h. La un alt grup de 13 subiecti, s-a observat o durata de somn de 8.1 h, cu o abatere de 1.9 h. Ne propunem sa studiem dispersia in aceste doua grupe.

Avem:

s s

n₁ = n₂ = 11

Formam raportul dispersiilor:

Raportandu-l la tabelele Sndcor, pentru g = n₁ - 1 = 10 si g = n₂ - 1 = 12, se gaseste valoarea limita pentru F, cu o probabilitate de 0.05 (adica 5 sanse din 100 de a fi depasita datorita fluctuatiilor fortuite), ca fiind F_0.05 = 2.76. Valoarea gasita pentru F, egala cu 1.46, este net inferioara. Nu exista deci diferenta semnificativa intre cele doua dispersii observate.

2. Analiza dispersiei

Analiza dispersiei isi propune sa studieze in ce masura diferentele observate intre valorile mediilor din fiecare grup traduc real o diferenta a actiunii intre diferitele clase testate, factor in functie de care se deosebesc diferitele grupuri, si nu sunt legate doar de fluctuatiile de esantionaj. Se pune problema compararii mediilor.

Fara indoiala, pentru a rezolva aceasta problema, ne propunem sa comparam mediile din aceste grupuri, doua cate doua. Dar exista un procedeu care ne permite sa testam omogenitatea multimii grupurilor studiate, adica de a face compararea simultana a acestor medii diferite si de a sti daca se poate sau nu sa le consideram ca apartinand unei aceleiasi populatii: este metoda numita "analiza dispersiilor", datorata statisticianului englez R. A. Fisher, si care are astazi o importanta deosebita, in particular pentru a exploata datele experimentale.

Principiul general al acestor probleme de comparare este testul "ipotezei nule", urmarind la toate esantioanele studiate apartinand aceleiaai populatii, in ce caz dispersia multimii este conditionata unic de fluctuatia de esantionaj.

Se vor analiza fluctuatiile individuale care se produc in interiorul unui grup, si intre doua grupuri.

A. Dispersia intra-grup

In interiorul fiecarui grup, fluctuatiile de esantionaj sunt reprezentate de abaterile (x - m) intre fiecare valoare individuala x si media m a grupului. Ramane sa consideram abaterile patratice (x - m)² (pentru care nu intervine semnul). Facand suma acestor abateri patratice pentru cele n valori individuale ale grupului, fie

se obtine un indice de fluctuatie care se produce in interiorul grupului.

Se face apoi suma acestor patrate pentru k grupe de esantion, obtinand un indice notat cu S₁², al dispersiei globale, introdus in multime pentru dispersia care exista in interiorul fiecarui grup.

Pentru a da acestei sume de patrate semnificatia generala a unei dispersii, trebuie sa o raportam la numarul de grade de libertate,

g = (n₁ - 1) + (n₂ - 1) + . + (n_k - 1)

= n₁ + n₂ + .+n_k - k

= N - k

Se obtine astfel dispersia numita "in grup", care se noteaza cu V_A si exprima dispersia introdusa in ansamblul de dispersii existente in interiorul fiecarui grup:

B. Dispersia inter-grupe

Daca se asimileaza toate valorile dintr-un grup la media m a grupului, se va anula efectul dispersiei in interiorul acestui grup, care va putea fi reprezentat prin media sa m.

In aceste conditii, abaterea fiecarei valori a grupului tratat in raport cu media generala a multimii esantionului studiat este (m - M), iar abaterea patratica este (m - M)².

Abaterea patratica globala a grupului, unificat pentru cele n valori, este S_q² = n (m - M)²

Facand suma abaterilor patratice ale celor k grupuri ale populatiei, se obtine un alt indice, notat cu S₂², si care reflecta dispersia introdusa in populatie de fiecare grup, considerat ca un tot:

Pentru a da acestei sume de patrate semnificatia generala a unei dispersii, trebuie sa o raportam la numarul de grade de libertate, g = k - 1.

Se obtine astfel dispersia inter-grup, notata cu V_B, care exprima dispersii ale grupului la grup:

C. Compararea dispersiilor

Dispersia intra-grup si cea inter-grup sunt doua elemente care conditioneaza fluctuatia multimii. Daca toate grupurile apartin unei aceleiasi populatii de origine, cele doua dispersii nu vor putea sa se abata una de la alta decat intr-o anumita masura, permisa de fluctuatia de esantionaj. De la aceasta limita, posibil de calculat, va fi normal sa consideram ca abaterea intre cele doua dispersii este prea importanta pentru a putea fi atribuita numai fluctuatiei fortuite.

Problema ramane de a testa divergenta intre doua dispersii, ceea ce se face prin studiul raportului dispersiilor de comparat. Se va forma raportul V_A/V_B (sau V_B/V_A, daca V_B>V_A) si se compara acest raport cu valorile date in tabelele Sndcor pentru pragul de semnificatie cu un coeficient de securitate de 95% (sau 99%). Daca acest raport este superior pragului de semnificatie, se respinge ipoteza populatiei unice si se admite ca diferentele constatate sunt semnificative.

Exemplu:

Se dozeaza corticoizii urinari la 40 subiecti de sex feminin, care au fost repartizati in functie de greutate in 4 grupe, comportand fiecare cate 10 subiecti:

I  : 50 59 kg;

II : 69 kg;

III : 79 kg;

IV : 89 kg.

Tabelul 8.8 da rezultatele obtinute (in mg/24 h).

Tabelul 8.8: Corticoizii urinari la 40 subiecti de sex feminin

Se cere sa determinam daca diferentele observate intre medii sunt semnificative si deci factorul "greutate" in functie de care s-au diferentiat aceste grupe are o influenta asupra marimii corticoizilor urinari.

Se pot compara mediile doua cate doua, aplicand Testul t (Student) pentru esantioane mici, dar acest procedeu este lung (trebuiesc facute 6 comparatii); in plus, se neglijeaza informatia continuta in ansamblul datelor, pentru ca nu intervin de fiecare data decat 10+10=20 dintre ele. Procedeul de analiza a dispersiei ne permite in schimb sa testam ipoteza unica intr-o singura operatie.

Calculam dispersia intra-grup, V_A :

Se calculeaza mai intai abaterea patratica in fiecare grup. Se gaseste:

Calculam dispersia inter-grup, V_B :

Mai intai calculam media generala, M:

Apoi determinam abaterile patratice din grup:

Se formeaza raportul dispersiilor (tinem cont ca V_B > V_A) :

Tabelele Sndcor arata pentru g g_B = k -1= 3 si g g_A = N - k = 40 - 4 =36, valoarea limita a lui F cu un prag de probabilitate de 0.05 ca fiind F_0.05 = 2.9, si cu un prag de probabilitate de 0.01 ca fiind F_0.01 = 4.6. Se observa ca valoarea calculata a lui F este net superioara lui F_0.05 si lui F_0.01.

O astfel de divergenta are deci mai putin de o sansa din 100 de a se produce ca urmare a fluctuatiilor fortuite intr-o populatie unica. Deci, ipoteza de mai sus trebuie inlaturata, si vom admite ca grupurile apartin unor populatii diferite; diferentele constatate sunt inalt semnificative, iar factorul greutate are o influenta reala asupra marimii corticoizilor urinari.

3. Compararea valorilor medii (testul t - Student)

Pentru a lamuri problema daca divergenta valorilor unui anumit parametru x este intamplatoare sau nu, se efectueaza doua serii de experimente si pentru fiecare serie de rezultate se calculeaza media aritmetica a parametrului, adica si . Problema care se pune este, deci, de a decide cand socotim ca diferenta intre aceste medii este suficient de mare pentru ca practic sa se poata afirma ca deosebirile constatate in calitatea parametrilor nu sunt intamplatoare.

Masuratorile se presupun independente si, cel putin in cadrul fiecarei serii, de egala precizie, iar functia de repartitie a erorilor de masurare se presupune a fi normala.

Presupunem ca s-au efectuat n₁ masurari independente de egala precizie intr-o prima serie de masurari si n₂ in cea de a doua serie de masurari (cu dispersiile s₁² si, respectiv, s₂²). Notam cu si mediile aritmetice ale rezultatelor din prima si din cea de a doua serie.

Pentru a raspunde la problema daca diferenta dintre aceste medii aritmetice este intamplatoare sau nu, vom calcula raportul:

Fixam un interval de incredere P si corespunzator determinam din tabelele pentru testul t, valoarea t = t(P

Exemplu:

Pentru P Þ t = 2.576

Daca valoarea absoluta a lui t calculat, t_calculat > t(P)_tabel, urmeaza ca diferenta mediilor aritmetice se poate considera ca nefiind intamplatoare. In caz contrar, nu avem motive sa consideram ca diferenta este semnificativa (adica ea poate fi considerata ca o abatere intamplatoare).

Exemplu:

Sa consideram doua serii, de cate 25 si 30 de masuratori.

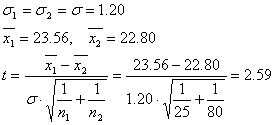
t(0.99)_tabel = 2.576, deci t(0.99)_tabel < t_calculat si rezulta cu o certitudine de 0.99 ca diferenta intre medii este semnificativa.

4. Compararea dispersiilor (testul Fisher)

Cand se efectueaza masurari in conditii diferite, apare problema compararii preciziei masurarilor. In particular apare problema compararii preciziei de masurare a diferitor aparate. Importanta acestei probleme este subliniata indeosebi de faptul ca intervalele de incredere ale abaterilor medii patratice se dovedesc a fi mari.

Presupunem ca in doua serii de masurari s-au obtinut dispersiile empirice ale datelor:

S₁² : pentru k₁ grade de liertate;

S₂² pentru k₂ grade de libertate.

(in general, primul coeficient se refera la dispersia empirica cu valoarea cea mai mare).

Se va calcula raportul:

Se alege un interval de siguranta P = 0.95 sau P = 0.99, si se determina valoarea critica F, corespunzatoare numerelor gradelor de libertate k₁ si k₂ . Valoarea calculata a lui F, F_calculat pentru seriile observate va fi comparata cu valorile extrase din tabel, corespunzatoare intervalelor de incredere alese, F(P)_tabel ; apar doua situatii posibile:

F_calculat  > F(P)_tabel Þ diferenta intre medii nu este aleatoare;

F_calculat < F(P)_tabel Þ diferenta intre medii este aleatoare, si nu are o semnificatie speciala.

5. Testul Z (pentru procente)

Testul furnizeaza o estimare numerica a probabilitatii ca diferenta observata sa survina sau nu datorita hazardului.

Se calculeaza urmatorul coeficient, Z, pentru compararea a doua procentaje P₁ si P₂, cu erorile standard SE₁, SE₂.

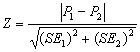
Daca Z ³ , atunci se poate afirma cu un prag de semnificatie de 5% ca cele doua procentaje difera nu datorita hazardului, ci datorita unei cauze care trebuie determinata.

Daca Z ³ , atunci se poate afirma cu un prag de semnificatie de 1 % ca cele doua procentaje difera nu datorita hazardului, ci datorita unei cauze care trebuie determinata.