Arbori - Arbori binari de cautare

I.1          Arbori

I.1.1         Prezentare generala

Arborii sunt, ca si listele, o colectie de natura dinamica, recursiva si neliniara de noduri. Ei sunt asemanatori cu cei din natura, cu deosebirea ca, in informatica, arborii se ramifica ("cresc") in jos (asemenea arborilor genealogici).

Modul de organizare a nodurilor unui arbore respecta urmatoarele proprietati:

un singur nod al arborelui nu are descendenti, el se numeste radacina arborelui;

toate nodurile formeaza sub-arbori disjuncti intre ei.

Astfel, dintr-un nod (denumit nod-tata) se pot forma, descendent, alte noduri, numite fiii nodului-tata in cauza. Fiii unui nod sunt frati. Numarul de fii ai unui tata defineste ordinului nodului tata. Nodurile de ordin 0, deci care nu au fii, se numesc noduri terminale sau frunze.

Spunem ca radacina arborelui se afla pe nivelul 0, fiii sai pe nivelul 1, , daca un nod are nivelul n atunci fiii sai se afla pe nivelul n+1.

Fig. I . Structura in forma de arbore.

I.1.2         Arbori binari

Un caz aparte de structura arborescenta il constituie arborii binari, in care fiecare nod are cel mult doi fii, denumiti fiul stang si fiul drept. Acestia formeaza, la randul lor, subarborele stang, respectiv drept. Daca un fiu al unui nod tata lipseste, el este considerat nul. Frunzele au amandoi fiii nuli. Daca un nod are amandoi fiii nenuli, cheile acestora se afla intr-o relatie de ordine dependenta de natura problemei.

Trebuie facuta observatia ca arborii binari sunt frecvent intalniti in practica si ca orice arbore (oarecare) poate fi transformat intr-un arbore binar.

Ca si in cazul listelor, un nod contine, pe langa informatia propriu-zisa, adresele celor doi fii.

Fig. I . Continutul nodurilor unui arbore binar

Declaratia unui nod intr-un arbore binar este (in C++):

struct TNod;

Operatiile fundamentale ce se definesc pe arborii binari sunt:

inserarea unui nod frunza;

accesul la un nod;

stergerea unui nod;

stergerea arborelui;

parcurgerea arborelui.

Trei modalitati de parcurgere prezinta interes:

parcurgerea in inordine (SRD)-se traverseaza mai intai subarborele stang, apoi este vizitata radacina (se prelucreaza informatia continuta in radacina) si, in cele din urma, se traverseaza subarborele drept;

Pentru ca arborii au, prin definitie, natura recursiva, este oportuna o implementare recursiva pentru parcurgere:

void ParcurgereSRD(TNod* rad)

In exemplul de mai sus, parcurgerea in inordine va genera iesirea: 3, 5, 7, 11, 13, 17, 19, 23.

parcurgerea in preordine (RSD) - se viziteaza radacina, se traverseaza subarborele stang, apoi cel drept;

void ParcurgereRSD(TNod* rad)

In exemplul de mai sus, parcurgerea in preordine va genera iesirea: 17, 5, 3, 11, 7, 13, 19, 23.

Parcurgerea in preordine a arborilor oarecare (nu neaparat binari) este asociata ordinii dinastice sau a ordinii succesiunii la tron. La moartea unui rege, tronul este mostenit de catre primul dintre fiii sai, daca acesta moare, atunci tronul revine descendentilor sai, in ordinea varstei si numai daca toti acestia mor, tronul revine, dupa aceeasi regula, celorlalti fii ai regelui din varful dinastiei. Este interesant de stiut faptul ca legile Angliei permit accesul la tron si al femeilor, insa in urma tuturor barbatilor.

parcurgerea in postordine (SDR) - se traverseaza subarborele stang, apoi cel drept si, in final, se viziteaza radacina.

void ParcurgereSDR(TNod* rad)

In exemplul de mai sus, parcurgerea in inordine va genera iesirea: 3, 7, 13, 11, 5, 23, 19, 17.

Stergerea arborelui necesita parcurgerea si stergerea fiecarui nod. Procedura accepta o implementare recursiva simpla si este asemanatoare, din motive lesne de inteles, cu parcurgerea in postordine (SDR):

void StergereArbore(TNod *rad)

Trebuie facuta observatia ca aceasta functie recursiva nu anuleaza pointerul catre radacina arborelui. Aceasta trebuie facuta explicit in functia apelanta.

Celelalte operatii intr-un arbore binar depind de relatia de ordine intre cheile fiilor unui nod. Vom exemplifica aceste operatii pentru arborele binar de cautare, intr-o alta sectiune.

I.1.3         Arborii (binari) de cautare

Arborii binari de cautare au particularitatea: cheia oricarui nod tata este mai mare decat oricare cheie din sub-arborele stang (daca exista) si mai mica decat oricare cheie a sub-arborelui drept (daca exista). In plus, arborii de cautare sunt utilizati atunci cand datele stocate au chei distincte.

Arborii de cautare au aplicatii in domenii foarte vaste. Un exemplu imediat ar fi crearea dictionarului unei limbi, in care fiecare cuvant reprezinta un nod in arbore. Verificarea corectitudinii unui cuvant se face prin cautarea sa in arbore. In functie de prefixul cuvantului se alege, la un moment dat, pe care sub-arbore (stang sau drept) se continua cautarea. In mod similar se poate crea un arbore cu cuvinte cheie (de exemplu taguri HTML), ce va fi ulterior utilizat pentru facilitati de editare de tip "auto-complete".

Se poate demonstra, prin inductie matematica, faptul ca este suficient sa consideram ca intr-un arbore de cautare cheia oricarui nod tata este mai mare decat cheia fiului stang si mai mica decat cea a fiului drept, acolo unde acestia exista.

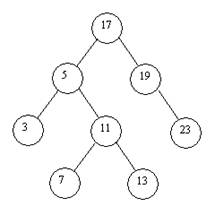
Fig. I . Arbore de cautare. Cheia oricarui nod-tata este mai mare decat toate cheile din subarborele stang si mai mica decat cele ale sub-arborelui drept.

Prin parcurgerea in inordine (SRD) a unui arbore de cautare se obtine colectia de date ordonata crescator dupa cheie.

In exemplul de mai sus, parcurgerea in inordine va genera sirul: 3, 5, 7, 11, 13, 17, 19, 23.

Adaugarea unei frunze intr-un arbore de cautare se face dupa urmatorul algoritm:

Pentru a vizualiza mai bine fenomenul, sa presupunem ca dorim sa construim un arbore de cautare pentru numere intregi. Consideram sirul: 17, 19, 5, 11, 7, 23, 3, 13. Iata mai jos, reprezentate grafic, etapele prin care se va construi arborele:

g. I . Construirea unui arbore de cautare prin adaugarea de noduri.

Accesul la un nod al arborelui de cheie data se face similar cu adaugarea. Tocmai rapiditatea cautarii, care are la baza tehnica Divide et Impera, prin injumatatirea la fiecare nivel a domeniului de cautare, a dat denumirea acestui tip de arbore.

I.1.4         Aplicatie

Sa se realizeze un arbore de cautare care ordoneaza crescator cuvintele dintr-un text si afiseaza frecventele lor de aparitie. Cuvintele sunt separate prin spatii sau prin semne de punctuatie. Aplicatia va trata caracterele in maniera case insensitive.