| CATEGORII DOCUMENTE |
Sistem automat. Structuri de sisteme automate
Sistemul automat este un caz particular de
sistem, la care relatia de cauzalitate u
![]()
Structura inchisa a unui sistem automat, la care comparatia intre marimi se face liniar (prin diferenta), este reprezentat in fig.1.4.
Sistemul S2, adica sistemul conducator (sau instalatia de automatizare), are in structura sa mai multe subsisteme (S21, S22, S23 si S24) care sa genereze marimea de executie m, in concordanta cu programul impus de marimea prescrisa q si marimea de iesire y.
Sistemul elementar S22 asigura comparatia valorilor marimii de intrare i, valori dorite pentru marimea de iesire y, cu valorile obtinute pentru aceasta.
Marimea є este abaterea sau eroarea dintre valorile dorite si valorile obtinute, pentru marimea y. Ea este obtinuta la iesirea sistemului S22, prin diferenta dintre marimea de referinta i si marimea de iesire y, si prelucrata de sistemul S23 care formeaza marimea de comanda u.
Adaptarea la proces a variabilei de comanda u se realizeaza prin intermediul sistemului de executie S24. Astfel, prin intermediul marimii de executie m, careia i se asociaza in general un flux energetic, se actioneaza asupra procesului condus S1.
Se observa ca reactia sistemului automat inchis este negativa. Aceasta asigura filtrarea perturbatiilor, cresterea preciziei, reducerea efectelor neliniaritatilor etc.
y q u p S m S S S S S i

Fig.1.4. Structura inchisa a unui sistem automat.
In caz general, schema bloc functionala a unui sistem automat inchis se reprezinta ca in fig.1.5.
p q i u m Ti S EE P EC RA EE Tr r

y
Fig.1.5. Schema bloc a unui sistem automat inchis.
Elementele sistemului automat inchis sunt urmatoarele:
Traductorul de intrareTi primeste marimea prescrisa q, ce reflecta valoarea dorita pentru marimea de iesire y,.si formeaza marimea de intrare i, iar traductorul de reactie Tr primeste marimea de iesire y si formeaza marimea de reactie r,
y p i u S EC RA F=EE+P+Tr
 Schema functionala a unui sistem
SA se simplifica si mai mult daca elementul de executie, traductorul
de iesire si procesul sunt grupate intr-un singur bloc, notat cu F
(vezi fig.1.6). Ansamblul rezultat in urma gruparii F=EE+P+Tr se
numeste parte fixata.
Schema functionala a unui sistem
SA se simplifica si mai mult daca elementul de executie, traductorul
de iesire si procesul sunt grupate intr-un singur bloc, notat cu F
(vezi fig.1.6). Ansamblul rezultat in urma gruparii F=EE+P+Tr se
numeste parte fixata.
Fig.1.6. Schema bloc simplificata a unui sistem automat inchis.
Structura evidentiaza faptul ca marimile masurate sunt transmise direct la intrarea sistemului de interpretare decizionala (EC+RA).
Sistemele automate inchise cu structurile prezentate mai sus sunt sisteme automate de reglare dupa eroare.
Cand o marime perturbatoare p importanta (cum este consumul, in cazul unor instalatii), ce actioneaza asupra procesului, este cunoscuta si usor masurabila se poate folosi un sistem automat de reglare combinata (vezi fig.1.7).
In cazul unui astfel de sistem, reglarea se face dupa eroare, cu compensarea marimii perturbatoare.
Pentru compensarea marimii perturbatoare p, partea fixata F s-a sectionat in doua parti:
F1, partea din F care nu este influentata de p, si
F2, partea din F care este influentata de p.
Marimea perturbatoare este masurata cu un traductor Tp, numit traductor de perturbatie, iar cu un regulator RP, numit regulator de perturbatie, se formeaza o marime up care insumata algebric cu marimea de comanda uε formeaza marimea de comanda u= uε - up, marime de intrare pentru sectiunea F1 a partii fixate.
Dupa F1, se obtine o marime care are doua componente: una datorata lui uε, care se transmite la iesirea sistemului, si una provenita de la up, care are rolul de a compensa marimea perturbatoare p.
y p i u EC RA F1 F2 RP Tp up u

Fig.1.7. Schema bloc simplificata a unui sistem automat de reglare combinata.
Ecuatia diferentiala
Pentru un element (sistem) liniar si continu monovariabil (ELCM
u y ELCM

Fig.2.1.
forma generala a ecuatiei diferentiale ce-i caracterizeaza functionarea este:
![]()
unde:
u(t), y(t) sunt variabilele de intrare si iesire;
ai(t), bj(t) sunt parametrii sistemului (coeficientii ecuatiei diferentiale).
In cazul unui element invariant, coeficientii ai si bj sunt constanti in raport cu timpul.
Pentru elementele des intalnite in practica, ecuatiile diferentiale ce caracterizeaza functionarea lor sunt:
Elementul proportional (sau tip P) este caracterizat de ecuatia:
![]()
sau
![]()
unde se scoate in evidenta factorul de amplificare (sau coeficientul de trasfer):
![]()
care este definit pentru regimul stationar.
Elementul integrator (sau tip I) este caracterizat de ecuatia:
![]()
sau
![]()
sau
![]()
unde T este constanta de timp (de integrare):
![]()
Elementul derivativ (sau tip D) este caracterizat de ecuatia:
![]()
sau
![]()
unde T este constanta de timp (de derivare):
![]()
Elementul de intarziere de ordinul I este caracterizat de ecuatia:
![]()
sau daca se scot in evidenta factor de transfer k si constanta de timp T:
![]()
unde:
![]()
![]()
Elementul de intarziere de ordinul II este caracterizat de ecuatia:
![]()
sau
![]()
sau
![]()
unde:
![]()

![]()


Pentru a
evidentia semnificatia fizica a parametrilor ζ si ωn consideram sistemul mecanic din fig.2.2,
unde, daca h este deplasarea masei in miscare M,
![]()
![]()
|
|
Pentru un sistem automat (fig 2.3) modelul matematic al structurii se obtine prin eliminarea variabilelor intermediare: ,u,m. Se obtine, astfel, o ecuatie diferentiala de forma:
![]()
unde ai si bj sunt determinati de parametrii procesului, regulatorului si elementului de executie:
h F M f k

Fig.2.2. Sistem mecanic.
Pentru proces modelul matematic liniarizat poate fi de tip element de intarziere de ordinul intai, doi sau mai mare. In caz general, acesta are forma:
![]()
y i u m S EE P EC RA EE r

Fig.2.3.
Pentru elementul de executie modelul matematic poate fi de tip: element proportional, element integrator sau element de intarziere de ordinul intai. In cazul elementelor integratoare, ecuatiile diferentiale pot fi de forma:
![]()
![]()
Pentru regulatoarele automate tipizate, ecuatiile de functionare sunt date in tabelul 2.1, unde kR, Ti, Td sunt parametrii de acordare ai regulatorului.
|
Regulator automat tipizat |
Tip |
Ecuatie de functionare |
|
Proportional |
P |
|
|
Proportional-integral |
PI |
|
|
Proportional-derivativ |
PD |
|
|
Proportional-integral-derivativ |
PID |
|
Tabelul 2.1. Ecuatii de functionare pentru regulatoarele automate tipizate.
Observatie: In regim stationar, intre valorile yst si ist ale marimilor de iesire si, respectiv, intrare se stabileste relatia:
![]()
adica
yst = ist.
Pentru calculul raspunsului sistemului, se rezolva ecuatia diferentiala determinand, pentru marimea de iesire, cele doua componente fortata si libera, notate cu yf si, respectiv, yl . In caz general, rezulta:
![]()
unde Ci sunt constante de integrare, ce se determina tinand cont de conditiile initiale, iar pi sunt radacinile ecuatiei caracteristice aferente sistemului.
Functia de transfer
Functia de transfer este un alt model matematic, de tipul intrare iesire, utilizat pentru caracterizarea functionarii sistemelor liniare si continue, obtinut cu ajutorul transformatei Laplace.
2.2.2.1. Definirea functiei de transfer
Consideram ca ecuatia diferentiala ce caracterizeaza functionarea unui element liniar si continuu monovariabil este:
![]()
Aplicand ecuatiei de mai sus transformata Laplace directa, cu conditii initiale nule, se obtine:
![]()
unde U(s)=L[u(t)] si Y(s)=L[y(t)] sunt transformatele Laplace directe ale marimilor de intrare si, respectiv, iesire.
Prin definitie functia de transfer este raportul dintre transformata laplace directa a marimii de intrare si transformata Laplace directa a marimii de iesire, cu conditii initiale nule:

2.2.2.2. Interpretarea functiei de transfer
Daca pentru un element liniar, se cunosc functia de transfer si marimea de intrare, se poate determina marimea de iesire. Astfel, din relatia (2.24), rezulta:
![]()
de unde, aplicand transformata Laplace inversa, se obtine:
y(t)=L-1[H(s)U(s)] (2.26)
2.2.2.3. Exemple de functii de transfer
Pentru elementul proportional, din ecuatia diferentiala (2.3), rezulta functia de transfer:
![]()
2. Pentru elementul integrator, din ecuatia diferentiala (2.7), rezulta functia de transfer:
![]()
3. Pentru elementul derivativ, din ecuatia diferentiala (2.10), rezulta functia de transfer:
![]()
Pentru elementul de intarziere de ordinul I, din ecuatia diferentiala (2.13), rezulta functia de transfer:
![]()
Pentru elementul de intarziere de ordinal II, din ecuatiile diferentiale (2.17) si (2.18), rezulta functia de transfer:
![]()
Pentru fiecare regulator automat (RA) tipizat, functia de transfer,
![]()
este data in tabelul 2.2.
|
Tip RA |
Ecuatie de functionare |
Functie de transfer |
|
P |
|
|
|
PI |
|
|
|
PD |
|
|
|
PID |
|
|
Tabelul 2.2`. Functiile de transfer ale regulatoarelor automate tipizate.
2.2.2.4. Algebra functiilor de transfer
Conexiunea serie
Consideram n elemente conectate in serie (fig.2.4).
H (s) Hn(s) H (s) x x xn y u

Fig.2.4. Conexiune serie.
Avem, succesiv:
|
Y(s) |
= Hn(s) Xn-1(s) = |
|
= Hn(s) Hn-1(s) Xn-2(s) = |
|
|
. |
|
|
= Hn(s) Hn-1(s) . H2(s) X1(s) = |
|
|
= Hn(s) Hn-1(s) . H2(s) H1(s) U(s) |
|
Rezulta:
![]()
In concluzie, pentru un ansamblu de elementele conectate in serie, functia de transfer echivalenta este egala cu produsul tuturor functiilor de transfer.
Conexiunea paralel
Consideram n elemente conectate in paralel (fig.2.5). Avam relatiile :
|
X1(s) |
= H1(s) U(s) |
|
X2(s) |
= H2(s) U(s) |
|
. |
|
|
Xn(s) |
= Hn(s) U(s) |
|
Y(s) |
= X1(s) + X2(s) +.+ Xn(s)= |
|
= H1(s) U(s) + H2(s) U(s) + + Hn(s) U(s) = |
|
|
= [H1(s) + H2(s) + + Hn(s) ] U(s) |
de unde rezulta:
![]()
H (s) x y u H (s) x Hn(s) xn

Fig.2.5. Conexiune paralel.
In concluzie, pentru un ansamblu de elementele conectate in paralel, functia de transfer echivalenta este egala cu suma tuturor functiilor de transfer.
2.2.2.4.3. Conexiunea cu reactie
Consideram o conexiune cu reactie (fig.2.6).
Hd(s) y i Hr(s) r

Fig.2.5. Conexiune cu reactie.
Avem:
|
Y(s) |
= Hd(s) ε(s) = |
|
= Hd(s) (I(s) - R(s)) = |
|
|
= Hd(s) (I(s) - Hr(s) Y(s)). |
|
|
Y(s) |
= Hd(s) I(s) - Hd(s) Hr(s) Y(s) |
Grupand in membrul stang termenii care il contin pe Y(s), se obtine:
|
Y(s) + Hd(s) Hr(s) Y(s) = Hd(s) I(s) |
|
Y(s) (1+ Hd(s) Hr(s)) = Hd(s) I(s) |
de unde rezulta:
![]()
Daca reactia este unitara (fig.2.6.), rezulta functia de transfer:
![]()
Hd(s) y i

Fig.2.6. Conexiune cu reactie unitara.
Echivalarea unui sistem cu reactie neunitara cu un sistem cu reactie unitara
Functia de transfer a sistemului cu reactie neunitara din fig. 2.5, adica:
![]()
se poate pune sub forma:
![]()
de unde rezulta schema echivalenta din fig. 2.6.
Hd(s) Hr(s) y i r

Fig.2.7.
Observatie: Cum orice sistem cu reactie neunitara se poate echivala cu un sistem cu reactie unitara, in capitolele urmatoare se va considera ca sistemele au reactia unitara.
2.2.4.5. Expresii ale functiei de transfer
Dupa calculul functiei de transfer, aceasta se obtine ca un raport de doua polinoame:
![]()
Daca pentru fiecare polinom, se scoate factor comun termenul liber, se obtine:
![]()
unde
![]()
Daca a0=0, la numitor se scoate factor comun termenul a1s, iar la numarator termenul liber b0. Se obtine:
![]()
unde
![]()
Daca a =a1=0, la numitor se scoate factor comun termenul a2s, iar la numarator termenul liber b0. Se obtine:
![]()
unde
![]()
In caz general, pentru H(s), se poate considera expresia:
![]()
unde α=1, 2, 3 si P(0)=Q(0)=1.
Daca se pun in evidenta radacinile polinoamelor P(s) si Q (s), se obtine:
![]()
unde: -z1, -z2,., -zm sunt zerourile lui H(s), iar -p1, -p2,., -pn, sunt polii lui H(s).
Daca se noteza:
![]()
![]()

Prezenta de zerouri sau poli complexi poate fi evidentiata in expresia:

2.4.1. Caracteristica amplitudine-faza
Deosebit de importanta pentru analiza sistemelor automate este caracteristica amplitudine-faza (sau locul geometric de transfer sau diagrama Nyquist).
Pentru a putea
studia comportarea sistemelor automate, respectiv a elementelor lor, in
domeniul frecventelor, este necesar sa se faca reprezentarea
grafica a lui
![]()
![]()
![]()
![]()
![]()
![]()
2.4.1.1. Etapele trasarii caracteristicii amplitudine-faza
Trasarea caracteristicii amplitudine faza se face urmand urmatoarele etape:
a) Se face
![]()
![]()
b) Pentru
![]()
![]()
|
|
0+ |
+ |
|
|
| |||
|
|
c) In planul H(j
![]()
![]()
![]()
punctele
![]()
![]()
eventualele puncte de intersectie cu axele planului H(j
![]()
sensul de parcurgere al caracteristicii cand
![]()
3.1.1. Principalele performante din cadrul raspunsului indical
3.1.1.1. Indici de calitate pentru variatia treapta a semnalului de intrare
Pentru un semnal treapta aplicat la intrare, raspunsul ideal este tot de forma unui semnal treapta, eventual de alta valoare. In realitate, raspunsul are o forma de variatie diferita de treapta, de obicei acesta este periodic amortizat. In fig.3.1, pentru un semnalul de intrare treapta unitara, i(t), este reprezentat semnalul de iesire periodic amortizat, y(t).
t i(t) y(t)

Fig.3.1.
Observatie:In cele ce urmeaza, se va considera ca sistemul este cu reactie unitara si fara traductor de intrare.
Pentru aprecierea regimului stationar, indicele de calitate utilizat este:
- eroarea stationara,
notata cu
![]()
![]()
Pentru aprecierea regimului tranzitoriu, indicii de calitate utilizati sunt:
- timpul de raspuns
(timpul de stabilire, durata regimului tranzitoriu), notat cu tt,este timpul dupa care
valoarea absoluta a diferentei dintre marimea de iesire, y(t),
si valoarea ei de regim stationar, yst, devine mai mica si se mentine sub o
anumita limita
![]()
![]()
unde
![]()
Pentru yst = 1, conditia devine:
![]()
rezulta, ca regimul
tranzitoriu se considera incheiat atunci cand marimea de iesire
intra in zona delimitata de doua drepte paralele cu axa
absciselor, duse prin punctele de ordonate
![]()
![]()
t y(t) yst tt

Fig.3.2.
- suprareglarea, notata cu
![]()
![]()
unde yM este valoarea maxima a marimii de iesire.
Daca yst =1, iar suprareglarea nu este exprimata in procente, rezulta (fig.3.3):
t y(t) Yst yM

![]()
Fig.3.3.
- gradul de amortizare, notat cu
![]()
![]()
Observatie La un sistem automat, este de dorit ca acesti indici de performanta sa fie cat mai mici.
3.1.1.2. Indici de calitate pentru variatia treapta a perturbatiei
In acest caz, performantele se definesc in mod asemanator cu deosebirea ca marimea de iesire nu pleaca din zero ci de la o anumita valoare stationara yst1, stabilindu-se in final la o valoare yst2 egala, sau diferita, cu yst1 (fig.3.4).
yst yst t y(t)

Fig.3.4.
Pentru regimul tranzitoriu, in
acest caz, este importanta valoarea abaterii maxime
![]()
Pentru regimul stationar este importanta caracteristica statica yst = f(p), unde p este marimea perturbatoare. In fig. 3.5, sunt reprezentate doua caracteristici statice, aproximate prin drepte. Variatia lui yst in functie de perturbatie se numeste statism si este dat de relatia:
![]()
astatice statice p yst

Fig.3.5.
Sistemele la
care
![]()
![]()
3.1.1.3. Indici de calitate globali (integrali)
In loc sa se foloseasca mai multi indici de performanta locali, se poate utiliza un indice integral (global). De exemplu, pentru caracterizarea erorii, se poate folosi indicele integral:
![]()
Valorile pentru acest indice sunt date de ariile hasurate din figurile 3.6.a, pentru un raspuns aperiodic, sau 3.6.b, pentru un raspuns periodic amortizat.
Daca, in cazul din fig.3.6.a, acest indice este eficient, in cazul din fig.3.6.b, indicele da erori grosolane, deoarece suma ariilor pozitive (de sub axa) si negative (de deasupra axei) poate avea o valoare mica, chiar si in cazul in care raspunsul se amortizeaza greu. Acest neajuns face ca, in cazul in care raspunsul este ca cel din fig.3.6.b, indicele de performanta I1 sa nu poata fi folosit.
t y(t) yst y(t) t y(t) yst y(t)

a) b)
Fig.3.6.
Cand raspunsul este periodic amortizat, se pot folosi indicii de performanta de forma:
![]()
sau
![]()
Deoarece eroarea are o influenta predominanta la valori mici ale timpului, se pot utiliza indici de performanta ponderati in timp, cum ar fi:
![]()
sau
![]()
In functionarea sistemelor automate, se doreste ca valorile indicilor integrali sa aiba valori cat mai mici.
3.2.2. Criterii de stabilitate
Criteriile de stabilitate pot fi algebrice sau frecventiale, cele mai utilizate dintre acestea fiind criteriul algebric Hurwitz si criteriul frecvential Nyquist.
3.2.2.1. Criteriul de stabilitate Hurwitz
Criteriul Hurwitz porneste de la ecuatia caracteristica aferenta ecuatiei diferentiale ce caracterizeaza functionarea sistemului a carui stabilitate dorim s-o studiem. Daca ecuatia caracteristica este:
![]()
conform criteriului Hurwitz, o conditie necesara, dar nu suficienta de stabilitate este ca toti coeficientii ecuatiei caracteristice sa fie strict pozitivi, adica:
![]()
![]()
Daca cel putin un coeficient al ecuatiei caracteristice este negativ sau nul, sistemul este instabil.
Cand
conditia (3.24) este indeplinita, se continua studiul
stabilitatii cu intocmirea determinantului principal al lui Hurwitz,
notat cu
![]()
Pe diagonala principala, se pun coeficientii ecuatiei caracteristice, in ordine descrescatoare a puterilor lui s, incepand cu coeficientul lui sn-1 si terminand cu termenul liber a0;
Pe coloane, plecind de la diagonala principala, sub aceasta se pun coeficientii ecuatiei caracteristice in ordine crescatoare a puterilor lui s, iar deasupra acesteia, se pun coeficientii ecuatiei caracteristice, in ordine descrescatoare a puterilor lui s. Atunci cand coeficientii se epuizeaza, coloanele se completeaza cu zerouri.
Conform acestor reguli, se obtine determinantul:

Dupa
intocmirea determinantului principal al lui Hurwitz, studiul
stabilitatii se continua cu calculul tuturor minorilor lui
![]()
![]()


Se observa ca:
![]()
Dupa calcului tuturor determinantilor, se pot trage concluzii cu privire la stabilitate. Astfel, conform criteriului Hurwitz, sistemul studiat este stabil, daca toti coeficientii ecuatiei caracteristice, determinantul principal al lui Hurwitz si toti minorii acestuia situati pe diagonala principala sunt strict pozitivi, adica:
![]()
![]()
![]()
![]()
![]()
Daca un determinant este nul, sistemul este la limita de stabilitate.
Observatie Criteriul Hurwitz ne spune daca un sistem este stabil sau nu, dar nu ne da indicatii cu privire la rezerva de stabilitate, El nu ne spune cat de aproape sau de departe este sistemul de limita de stabilitate.
3.2.2.2. Criteriul de stabilitate Nyquist
Criteriul lui Nyguist utilizeaza, pentru studiul stabilitatii sistemului inchis, caracteristica amplitudine-faza sau caracteristicile logaritmice ale sistemului deschis.
Observatie: Se va considera ca sistemul automat in circuit inchis are reactia principala directa, adica are reactie unitara. Daca reactia principala nu este unitara, se face echivalarea sistemului cu un sistem cu reactie unitara (vezi 2.2.2.4.3).
3.2.2.2.1. Criteriul Nyquist aplicat pe caracteristica amplitudine-faza
Pentru studiul stabilitatii sitemelor automate cu reactie unitara, pe caracteristica amplitudine-faza a sistemului deschis, se poate aplica criteriul Nyquist in forma simplificata.
Criteriul
Nyquist simplificat: Un sistem
liniar si continuu este stabil, in stare inchisa, daca,
la parcurgerea caracteristicii amplitudine-faza in sensul cresterii
lui
![]()
Cand caracteristica
amplitudine-faza trece prin punctul
critic, sistemul este la limita
de stabilitate, iar cand, la parcurgerea caracteristicii
amplitudine-faza in sensul cresterii lui
![]()
3.3.1.1. Calculul erorii
Eroarea este singura performanta care se poate calcula in caz general.
Pentru un sistem automat cu reactie unitara (fig. 2.6
![]()
rezulta ca

In caz general, pentru H(s), se poate considera expresia (vezi 2.2.4.5):
![]()
unde
![]()
Din relatiile (3.48) si (3.49), rezulta:

Pentru diverse semnale de intrare, se obtin urmatoarele valori ale erorii:
Daca i(t)=1 (treapta
unitara), adica I(s)=
![]()

Daca i(t)=t (rampa unitara), adica I(s)=
![]()
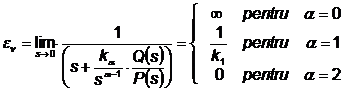
Daca i(t)=
![]()
![]()

Concluzie: Eroarea poate fi finita sau
infinita. Cand eroarea este finita, ea poate fi zero,
daca pe calea directa exista cel putin un element
integrator (adica
![]()
![]()
3.5. Corectia sistemelor automate liniare
Corectia, sau compensarea, urmareste imbunatatirea performantelor dinamice si statice ale unui sistem automat, atunci cand, experimental sau in urma analizei, rezulta ca aceste performante nu sunt satisfacatoare.
Corectia se poate realiza prin:
modificarea parametrilor sistemului (cel mai des se mudifica factorul de transfer al ramurii directe) sau
modificarea structurii (compensarea) sistemului prin introducerea unui element suplimentar de corectie (compensare).
Dupa efectuarea corectiei urmeaza in mod obligatoriu o etapa de analiza a sistemului corectat, etc.
La calcularea compensarii se dovedesc foarte utile metodele frecventiale.
Prin modificarea caracteristicilor de frecventa in domeniul pulsatiilor joase se modifica performantele regimul permanent, iar prin modificarea caracteristicilor de frecventa in domeniul pulsatiilor ridicate se modifica performantele regimului tranzitoriu.
Elementele de corectie se plaseaza cat mai aproape de inceputul legaturii directe deoarece, in acest caz, acestea sunt parcurse de semnale de mica putere si, ca atare, constructia lor este mai ieftina.
Elementele de corectie se pot plasa in serie, in paralel sau pe legaturi de reactie.
3.5.1. Metode de corectie a regimului tranzitoriu
In regim tranzitoriu, pot sa apara doua situatii:
Regim tranzitoriu prea lent, in care, din cauza unor amortizari excesive, raspunsul sistemului este aperiodic, cu durata de stabilire mare. In acest caz corectia se face prin cresterea factorului de transfer al legaturii directe (scade si eroarea stationara, daca aceasta este finita si diferita de zero).
Regim tranzitoriu slab amortizat cu oscilatii care se sting greu. In acest caz, corectia se realizeaza, mai dificil, prin micsorarea factorului de transfer (creste eroarea stationara) sau prin compensare. De obicei, se urmareste imbunatatirea gradului de stabilitate.
3.5.1.1. Corectarea regimului tranzitoriu prin micsorarea factorului de amplificare al sistemului deschis
Pentru exemplificare, consideram sistemul a carui stabilitate este studiata in cadrul paragrafelor 3.2.2.1.1 si 3.2.2.2.1.1. Functia de transfer de pe calea directa a sistemului era:
![]()
iar, pentru stabilitate, era necesara verificarea conditiei:
![]()
Evident, din relatia (3.101), rezulta ca micsorarea lui k conduce la imbunatatirea stabilitatii. Cum, prin micsorarea lui k, din H(s) se obtine Hc(s) (fig.3.14), caracteristica-amplitudine faza a sistemului deschis se modifica in totalitate. Aceasta inseamna ca micsorarea lui k modifica atat performantele regimului tranzitoriu, cat si performantele regimului permanent.
(-1,j0) Re H(j jIm H(j Hc(s) H(s)

Fig.3.14.
3.5.1.2. Comanda dupa derivata (corectie serie)
In acest caz, in varianta cea mai simpla, se introduce un element de corectie de tip PD, in serie cu elementele de pe calea directa.
Observatie Un element de tip D nu se poate introduce deoarece, in regim permanent, se intrerupe legatura directa.
De exemplu, daca sistemul necorectat (un caz ideal) are in circuit deschis functia de transfer:
![]()
rezulta:
![]()
si, cu criteriul Nyquist, rezulta imediat ca sistemul inchis este la limita de stabilitate, deoarece caracteristica amplitudine-faza se suprapune cu axa reala negativa, deci trece prin punctul critic.
In serie cu elementele de pe calea directa, se introduce un element de corectie de tip PD, cu functia de transfer:
![]()
In circuit deschis, pentru sistemul corectat, functia de transfer rezulta:
![]()
Cum, pentru sistemul inchis, functia de transfer este:
![]()
cu unul din criteriile de stabilitate rezulta imediat ca sistemul inchis este stabil
3.5.1.3. Imbunatatirea regimului tranzitoriu prin utilizarea unor reactii suplimentare
Utilizarea unor reactii rigide (de tip P) sau elastice (de tip D), pot determina imbunatatirea regimului tranzitoriu. Reactiile rigide pot cuprinde unul sau mai multe elemente de pe calea directa, iar reactiile elastice pot cuprinde toata calea directa (reactie dupa viteza).
3.5.1.3.1. Reactia rigida
Pentru exemplificare, consideram ca unui element de intarziere de ordinul I, situat pe calea directa, cu functia de transfer
![]()
i se aplica o reactie
negativa rigida (fig.3.15). Daca
![]()

Aceasta se poate pune sub forma:

unde
![]()
![]()
Se
constata ca elementul corectat este tot element de intarziere de
ordinul I, dar cu un factor de transfer mai mic si o
H1(s) y1 i1 Hc(s)

Fig.3.15.
Prin micsorarea factorului de transfer al elementului considerat, s-a micsorat si factorului de transfer al sistemului din care acesta face parte, deci sistemului i s-a marit rezerva de stabilitate, daca era stabil, sau a devenit stabil, daca era instabil (efect pozitiv).
Daca sistemul functioneaza cu eroare stationara, micsorarea factorului de transfer al sistemului conduce la cresterea erorii (efect negativ).
Prin micsorarea constantei de timp, elementul considerat a devenit mai rapid (efect pozitiv).
Se constata ca efectele sunt pozitive, in regim tranzitoriu, si negative, in regim permanent. Ideal ar fi ca reactia sa actioneze in regim tranzitoriu si sa nu actioneze in regim permanent. Acest lucru se poate realiza cu ajutorul reactiei elastice.
3.5.1.3.2. Reactia elastica
Reactia elastica actioneaza diferit in cele doua regimuri: tranzitoriu si permanent (stationar). Daca elementul de corectie este de tip D, se obtine o reactie elastica.
De
exemplu (fig.3.15), sa presupunem ca elementului cu functia de
transfer
![]()
![]()
![]()
rezulta:
![]()
Aplicand propritatile limitei, din relatiile (3.112) si (3.113), se obtine:

Din relatiile (3.113) si (3.114), rezulta ca
![]()
adica, in regim stationar (
![]()
3.5.2. Metode de corectie a regimului stationar
Calitatea regimului stationar se poate imbunatati prin:
cresterea factorului total de amplificare ceea ce, dupa cum s-a aratat in sectiunea 3.3.1.1, conduce la micsorarea erorilor in regim stationar;
cresterea
numarului de integrari pe calea directa (adica
![]()
calitatea elementelor componente, in special precizia traductoarelor, ceea ce conduce la micsorarea erorilor in regim stationar.
3.5.3. Conpensarea perturbatiilor
Consideram sistemul automat liniar din fig. 3.16. Asupra sistemului actioneaza o marime perturbatoare p. Pentru compensarea acestei marimi, a fost introdus blocul cu functia de transfer Hc(s).
y i + - u H (s) + + + - up u H (s) H (s) Hc(s) p

Fig. 3.16.
Avand in vedere structura sistemului, rezulta relatia:
Y(s) =H3(s) [ P(s) + H2(s) [ H1(s) [I(s) - Y(s)] - Hc(s) P(s) ] ] (3.115)
din care, dupa desfintarea parantezelor si regruparea termenilor, se obtine:
Y(s) [1+ H1(s) H2(s) H3(s)] = H1(s) H2(s) H3(s) I(s) - H3(s) [1 - H2(s) Hc(s)] P(s)
Rezulta:
![]()
Variatia marimii de iesire, determinata de marimea perturbatoare, este:
![]()
Evident,
pentru ca marimea perturbatoare sa nu influenteze mirimea de
iesire, este necesar ca
![]()
:
![]()
In practica, conditia (3.118) nu poate fi realizata decat in regim stationar, daca pentru factorul de transfer al elementului de compensare se alega valoarea
![]()
unde k2 este factorul de transfer al elementului cu functia de transfer H2(s)
Compensarea influenteaza calitatile dinamice si statice ale sistemului numai in raport cu perturbatia p. Ea ramane fara efect fata de celelalte perturbatii care actioneaza asupra sistemului.
Concluzie Cerintele care se impun pentru regimul tranzitoriu si pentru cel permanent sunt contradictorii. Realizarea unei corectii corespunzatoare trebuie sa asigure imbunatatirea simultana atat a regimului tranzitoriu cat si a regimului stationar.
Criteriul modulului, varianta Kessler, este un criteriu de acordare optima a regulatoarelor pentru procese rapide.
In cazul acestui criteriu, in functia de transfer a partii fixate, se pun in evidenta doua categorii de constante de timp:
constante de timp principale - notate cu Tk
, unde
![]()
constante de timp parazite - notate cu
![]()
![]()
Constantele de timp parazite sunt
considerate constantele cu valori foarte mici (sub o secunda), cea mai
mare
Daca in
![]()

unde
![]()
Deoarece
![]()
![]()
Notand:
![]()
se obtine:

Pornind de la satisfacerea intr-o masura cat mai buna a conditiilor criteriului modulului, in varianta Kessler, pentru a rezulta o acordare optima, se recomanda ca functia de transfer a regulatorului automat sa aiba expresia:

In acest caz, pentru calea directa, rezulta functia de transfer:
![]()
iar pentru sistemul inchis, se obtine functia de transfer:
![]()
adica un sistem cu doi poli.
Scotand in evidenta
pulsatia naturala
![]()
![]()

unde
![]()
![]()
Conform relatiilor (4.18) si (4.23), pentru suprareglaj si durata regimului tranzituri, se obtin valorile:
![]()

Rezulta ca sistemul rezultat are performante foarte bune pentru un semanal de intrare treapta si, in acelasi timp, o comportare buna in raport ce marimile perturbatoare.
Observatii:
1.
Daca functia de transfer a partii fixate contine o
singura
![]()
pentru regulatorul automat, se obtine functia de transfer:
![]()
adica un regulator de tip PI:

2. Daca functia de transfer a partii fixate contine doua constante de timp principale, adica:
![]()
pentru regulatorul automat, se obtine functia de transfer:
![]()
adica un regulator de tip PID:
![]()
3. Daca functia de transfer a partii fixate contine mai mult doua constante de timp principale, in urma acordarii cu criteriul modulului varianta Kessler nu se mai obtine un regulator tipizat.
Acest criteriu, elaborat tot de Kessler, este destinat acordarii optime a regulatoarelor pentru procese rapide in cazurile in care se impune o eroare stationara nula pentru intrare rampa.
Blocul de reglare este astfel proiectat incat, pentru sistemul deschis, rezulta functia de transfer:
![]()
Pentru intrare rampa, polul de
ordinul doi in origine conduce la
![]()
Dupa cum s-a aratat in cadrul sectiunii 4.2.1.1.1, in cazul utilizarii variantei Kessler a criteriului modulului, problema proiectarii sistemului poate fi rezolvata cu un regulator tipizat numai daca functia de transfer a partii fixate HF(s) contine cel mult doua constante de timp principale.
Atunci cand functia de transfer a partii fixate contine mai mult de doua constante de timp principale, problema acordarii poate fi rezolvata cu ajutorul regulatoarelor tipizate, daca se utilizeaza o schema de reglare in cascada (fig. 4.6).
u i + - RA y F F p F u + - RA

Fig. 4.6.
In
acest caz, partea fixata F este
impartita in mai multe parti intre care se transmit
anumite marimi intermediare. In fig. 4.6, F este impartita in F1 si F2,
iar
![]()
Impartirea partii fixate se face prin alegerea marimilor intermediare dupa criteriile:
Marimile intermediare sa fie usor masurabile prin mijloace tehnice simple (in schema au fost figurate reactii directe, in realitate, pe caile de reactie, sunt instalate traductoare).
Partile rezultate trebuie sa aiba functii de transfer cu cel mult doua constante de timp principale, pentru ca schema sa poata fi acordata cu regulatoare tipizate.
Prin
intermediul marimii intermediare
![]()
Schema, pe
langa faptul ca foloseste regulatoare tipizate, mai
prezinta avantajul ca raspunde mai repede in ceea ce priveste
anularea efectelor marimilor perturbatoare (durata regimului tranzitoriu a
scazut). Astfel, daca o marime perturbare p actioneaza asupra partii F1, marimea intermediara
![]()
In schemele de reglare in cascada acordarea optima se face incepand cu bucla cea mai interioara.
Presupunand
ca
![]()
![]()
Cum
![]()
![]()
Se obtine schema din fig. 4.7, in care bucla 2 a devenit bucla cea mai interioara.
u i + - RA y H (s) F p

Fig. 4.7.
Presupunand
ca
![]()
![]()
![]()
![]()
Se efectueaza acordarea regulatorul RA2 etc.
4.3. Metoda locului radacinilor
4.3.2. Reguli de trasare a locului radacinilor in cazul sistemelor cu reactie negativa unitara
Regula : Locul radacinilor cuprinde n ramuri distincte, n reprezentand gradul ecuatiei caracteristice aferente sistemului, deci numarul radacinilor acesteia.
Justificare: Cum ecuatia caracteristica (4.122) este de gradul n, aceasta are n radacini, deci locul radacinilor are n ramuri.
Regula : Locul radacinilor este simetric in raport cu axa reala.
Justificare: Cum ecuatia caracteristica are toti coeficientii reali, radacinile acesteia sunt pur reale sau coplex-conjugate, deci simetrice fata de axa reala. Rezulta ca si locul este simetric fata de axa reala.
Regula 3: Pentru k=0, ramurile locului radacinilor pornesc din polii sistemului in circuit deschis.
Justificare: Ecuatia (4.123), pentru k=0, devine:
![]()
Rezulta ca, pentru k=0, radacinile ecuatiei caracteristice sunt polii lui H(s).
Regula
4: Pentru
![]()
Justificare: Din ecuatia (4.123), prin impartire cu k, se obtine:
![]()
Rezulta ca, pentru
![]()
![]()
deci radacinile ecuatiei caracteristice se confunda cu zerourile lui H(s).
Regula 5: Pentru
![]()
![]()
![]()
Asimptotele se intersecteaza pe axa reala intr-un punct unic denumit "centru de greutate" al configuratiei zerourilor si polilor functiei de transfer H(s). Abscisa centrului de greutate se determina cu relatia:

Justificare: Din ecuatia (4.122), se obtine:
![]()
din care, dupa efectuarea impartirii, rezulta ecuatia
![]()
care are ca radacini cele n-m radacini, ale ecuatiei caracteristice, ce tind catre infinit.
Rezulta:

de unde se obtine:

Pentru ca cele n-m radacini tind la infinit, in ecuatia (4.133) se neglijeaza, in raport cu termenul ce-l contine pe sn-m, ceilalti termeni si se obtine:
![]()
sau
![]()
de unde rezulta cele n-m radacini care tind la infinit

unde
![]()
Din relatia (4.138), rezulta ca radacinile sunt situate pe un cerc a carui raza creste cu k. Razele pe care se deplaseaza radacinile ecuatiei caracteristice reprezinta directiile asimptotice care, evident, pornesc din centrul cercului si fac cu axa reala unghiurile.
![]()
Regula 6: Locul radacinilor contine toate portiunile axei reale care se afla la stanga unui numar impar de poli si zerouri.
Justificare: Consideram in planul s o repartitie pentru polii si zerourile lui H(s) ca in fig. 4.8. Fie punctul M(s) situat pe axa reala. Se observa ca:
pentru o pereche de poli (sau zerouri)
complecsi conjugati situati in dreapta punctului M, suma argumentelor fazorilor cu varful
in M este de 2p. De exemplu, pentru polii p2 si p3, suma argumentelor este:
![]()
pentru un pol (sau zerou) situat pe axa reala in dreapta punctului M argumentul este p ( de exemplu, pentru zeroul z1);
pentru un pol (sau zerou) situat pe axa reala in stanga punctului M argumentul este zero ( de exemplu, pentru polul p1).
M +j p z p p Planul
s
 SHAPE * MERGEFORMAT
SHAPE * MERGEFORMAT 
Fig. 4.8.
In relatia (4.126) argumentele fazorilor corespunzatori zerourilor intra cu semnul plus, iar argumentele fazorilor corespunzatori polilor intra cu semnul minus.
Oricum s-ar insuma algebric (cu
semnul plus sau minus)
un numar impar de valori p, se obtine un rezultat de forma (2l+1) p, unde l
![]()
Rezulta ca, daca punctul M este situat pe axa reala in stanga unui numar impar de poli si zerouri, el apartine locului pentru ca in acest caz conditia (4.126) este verificata.
Regula 7: Valoarea lui k, pentru care locul radacinilor intersecteaza axa imaginara a planului s, se determina din conditia:
![]()
unde
![]()
Justificare: Cand radacinile
ecuatiei caracteristice sunt situate pe axa imaginara, sistemul este
la limita de stabilitate, deci
![]()
Observatie: In
acest caz, radacinile pot fi determinate, daca in ecuatia
caracteristica se face
![]()
Regula 8: Daca o portiune a axei reale, cuprinsa intre doi poli adiacenti ai sistemului deschis, apartine locului radacinilor, atunci ea va contine un punct de ramificare, de indepartare de axa reala (fig. 4.9.a).
Justificare: Din cei doi poli adiacenti, p1 si p2, pornesc doua ramuri distincte ale locului. Acestea se intalnesc in punctul de ramificare, de abscisa sr, dupa care se departeaza de axa reala, dupa care, se desprind doua ramuri ce corespund a doua radacini complex-conjugate ale ecuatiei caracteristice.
p p +j sr +j z z sr k = 0 k = 0 k = ∞ k = ∞

a) b)
Fig. 4.9.
Regula 9: Daca o portiune a axei reale, cuprinsa intre doua zerouri adiacente ale sistemului deschis, apartine locului radacinilor, atunci ea va contine un punct de ramificare, de apropiere de axa reala (fig. 4.9.b).
Justificare: In cele doua zerouri adiacente, z1 si z2, sosesc pe axa reala, din punctul de ramificare sr, doua ramuri distincte ale locului. Acestea provin din doua radacini complex-conjugate care, in punctul de ramificare, au devenit egale.
Regula 10: Daca o portiune a axei reale, cuprinsa intre un pol si un zero, apartine locului radacinilor, atunci ea constituie o ramura distincta a locului.
Justificare: Pentru k variind de la zero la infinit, punctul curent al locului se depleaseaza de la polul p1 la zeroul z1 (fig. 4.10).
+j z p k = 0 k = ∞

Fig. 4.10.
Regula 11: Coordonatele punctelor de ramificare ale locului sunt date de radacinile ecuatiei:
![]()
unde zi, pi sunt zerourile, respectiv polii, lui H(s), sr reprezinta coordonatele punctelor de ramificare de pe axa reala, iar r este numarul punctelor de ramificare.
Justificare: Intr-un punct de ramificare, ecuatia caracteristica (4.121) are o radacina dubla. Rezulta:

Eliminand k intre relatiile (4.142) se obtine
![]()
![]()
![]()
si
![]()
rezulta:
![]()
Regula 12: In punctul
de ramificare, doua ramuri ale locului parasesc, sau ating,
normal (sub un unghi de
![]()
Regula Unghiul de plecare,
![]()
![]()
![]()
![]()

respectiv

unde
![]()
![]()
Justificare: Relatiile (4.146) si (4.147) rezulta din conditia argumentelor (4.126)
5. Sisteme automate liniare multivariabile
5.1. Procese tehnologice cu mai multe marimi de iesire si intrare
In practica, majoritatea proceselor tehnologice sunt caracterizate de mai multe marimi de intrare si iesire impunandu-se reglarea mai multor marimi de iesire.
Corespunzator numarului de marimi de iesire din proces supuse reglarii, se impune si utilizarea unui numar adecvat de elemente de executie si de traductoare
Ansamblul format din elementele de executie, procesul tehnologic si traductoarele de masurare constitue partea fixata a unui sistem automat multivariabil.
In fig. 5.1, este reprezentata partea fixata F a unui astfel de sistem, unde u1, u2,., uq reprezinta marimile de comanda ale sistemului, y1, y2,., yl reprezinta marimile de iesire ale sistemului, iar p1, p2,., pn sunt marimi perturbatoare. In caz general, l≠q.
Elemente de executie Traductoare Proces tehnologic y y yl u u uq p p F

Fig. 5.1.
y y yl u u uq p p
 In
cazul partii fixate F,
fiecare marime de intrare poate influenta toate marimile de
iesire, rezultand, in interiorul acesteia, canale de transfer ale
semnalelor, ca in fig. 5.2.
In
cazul partii fixate F,
fiecare marime de intrare poate influenta toate marimile de
iesire, rezultand, in interiorul acesteia, canale de transfer ale
semnalelor, ca in fig. 5.2.
Fig. 5.2.
Cum partea fixata F este liniara, pentru fiecare canal de transfer se poate defini o functie de transfer:
![]()
![]()
Partea fixata F fiind liniara, marimile de iesire se calculeaza functie de cu l linii si q coloane

Acest sistem poate fi exprimat sub forma matriceal-vectoriala astfel:

respectiv:
Y(s) = HF(s) U(s) (5.4)
unde:
HF(s) - matricea de transfer a partii fixate multivariabile, cu l linii si q coloane;
Y(s) - vectorul coloana al transformatelor
U(s) - vectorul coloana al transformatelor
5.2. Parte fixata cu doua marimi intrare si doua marimi de iesire
Se considera partea fixata a unui astfel de sistem cu doua marimi intrare si doua marimi de iesire, adica l=q=2.
In acest caz, sistemul (5.2) devine:

din care, pentru partea fixata, se poate intocmi schema bloc din fig. 5.3.
Matricea de transfer a partii fixate are urmatorul aspect:
H(s) =

HF HF HF HF + + + + u u y y F

Fig. 5.3.
Regulatoare automate cu mai multe marimi de intrare si iesire
Regulatoarele automate, utilizate in sistemele automate multivariabile, au rolul de a asigura atat performantele impuse, pentru fiecare canal de legatura directa intrare-iesire, cat si de a compensa efectul perturbatiilor si interactiunilor existente intre variabilele diferitelor canale intrare-iesire sau perturbare-iesire.
Necesitatea compensarii efectului interactiunilor dintre canale impune utilizarea unor regulatoare multivariabile. Utilizarea unor regulatoare monovariabile, destinate reglarii fiecarei marimi de iesire, reprezinta o solutie ce conduce la performante inferioare celor obtinute prin utilizarea unor regulatoare multivariabile.
Ingloband si elementele de comparatie in blocul regulatorului si presupunand ca reactiile principale sunt directe, se obtine schema bloc din fig. 5.4, unde F este blocul format din elementele de executie, traductoare si proces tehnologic, iar RA este blocul format de elementele de comparatie si regulatorul multivariabil.
y y yl u u uq p p i i iq - - RA F

Fig. 5.4.
S-a considerat ca F, blocul partii fixate, este supus si actiunii unor marimi perturbatoare p1, p2, , pn.
In cazul blocului RA, pentru diferitele canale de transmitere a semnalelor, se pot defini doua categorii de functii de transfer:
functii de transfer pentru canalele de la marimile de intrare i1, i2, , iq spre marimile de comanda u1, u2, , uq
![]()
functii de transfer pentru canalele de la marimile de iesire y1, y2, , yl, spre marimile de comanda u1, u2, , uq
![]()
Cu aceste functii de transfer, aplicand principiul suprapunerii efectelor, se obtin marimile de comanda:

sau sub forma matriceal-vectoriala.

respectiv:
U(s) = HRI (s) I(s) - HRE(s) Y(s) (5.11)
unde:
HRI (s) - matricea de transfer a regulatoarelor de intrare, cu q linii si q coloane;
HRE(s) - matricea de transfer a regulatoarelor de iesire, cu q linii si l coloane;
I(s) - vectorul coloana al transformatelor
Y(s) - vectorul coloana al transformatelor
U(s) - vectorul coloana al transformatelor
Matricea de transfer a unui sistem automat de reglare multivariabil
Conform relatiilor (5.4) si (5.11), structura unui sistem automat de reglare multivariabil are aspectul din fig. 5.5.
EC Y(s) U(s) I(s) HF(s) HRE(s) HRI(s) P(s)
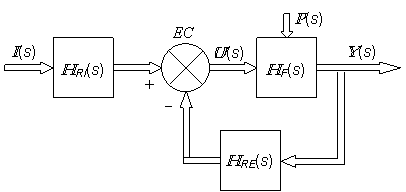
Fig. 5.5.
Din relatiile (5.4) si (5.11), rezulta succesiv relatiile matriceal-vectoriale:
Y(s) = HF(s) U(s) = HF(s) HRI (s) I(s) - HF(s) HRE(s) Y(s). (5.12)
Grupand in membrul stang termenii care contin vectorulY(s), se obtine relatia:
[ Il + HF(s) HRE(s) ] Y(s) = HF(s) HRI (s) I(s), (5.13)
unde Il este matricea unitate de ordinul l. Din relatia (5.13), rezulta vectorul:
Y(s) = [ Il + HF(s) HRE(s) ]-1 HF(s) HRI (s) I(s). (5.14)
Cum
Y(s) = H 0(s) I(s), (5.15)
rezulta matricea de transfer a sistemului automat de reglare multivariabil inchis:
H 0(s) = [ Il + HF(s) HRE(s) ]-1 HF(s) HRI (s). (5.16)
Elemente de sinteza a sistemelor automate de reglare multivariabile
5.5.1. Determinarea matricelor regulatoarelor
Scopul sintezei sistemelor multivariabile consta in obtinerea unei matrice dorite H 0(s), pentru o matrice HF(s) data.
Pentru aceasta, trebuiesc determinate matricile HRI (s) si HREI (s) rezolvand cele lq ecuatii rezultante din ecuatia matriceala (5.16).
Deoarece matricea HRI(s) are q2 elemente, iar matricea HRE(s) are lq elemente, rezulta ca determinarea matricelor HRI(s) si HRE(s) este echivalenta cu determinarea a q2+lq elemente.
Determinarea celor q2+lq elemente, prin rezolvarea sitemului de lq ecuatii rezultat din ecuatia matriceala (5.16), necesita introducerea de q2 conditii suplimentare.
Conditiile suplimentare se pot impune in trei moduri. Functie de modul de impunere a conditiilor suplimentare, rezulta variantele:
a) Daca l = q, adica daca numarul marimilor de intrare este egal cu numarul marimilor de iesire, se poate impune conditia:
HRI(s) = HRE(s) (5.17)
si pentru sistemul automat multivariabil se obtine structura din fig. 5.6.
EC Y(s) U(s) I(s) HF(s) HRI(s) P(s) E(s)

Fig. 5.6.
![]() In acest caz, relatia (5.16) devine:
In acest caz, relatia (5.16) devine:
H 0(s) = [ Iq + HF(s) HRI(s) ]-1 HF(s) HRI (s) (5.18)
Din relatia (5.18), se se obtin succesiv relatiile:
[ Iq+ HF(s) HRI(s) ] H 0(s) = HF(s) HRI (s), (5.19)
H 0(s) = HF(s) HRI (s) [ Iq - H 0(s) ], (5.20)
iar din relatia (5.20), rezulta matricele de transfer ale regulatoarelor:
HRE(s) = HRI (s) = [HF(s)]-1 H 0(s) [ Iq - H 0(s) ]-1. (5.21)
b) Daca l = q, se mai poate impune si conditia:
HRE(s)= Iq. (5.22)
In
acest caz, pentru sistemul automat multivariabil se obtine structura din
fig. 5.7, iar ![]()
H 0(s) = [ Iq + HF(s) ]-1 HF(s) HRI (s) (5.23)
de unde rezulta matricea de transfer a regulatoarelor de intrare:
HRI (s) = [HF(s)]-1[ Iq+ HF(s) ] H 0(s). (5.24)
EC Y(s) U(s) I(s) HF(s) HRI(s) P(s)
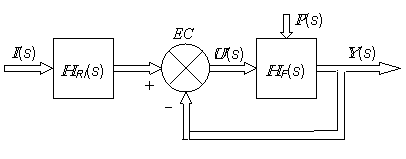
Fig. 5.7.
c) Daca l ≠ q, se poate impune conditia:
HRI(s)= Iq. (5.25)
si pentru sistemul automat multivariabil se obtine structura din fig. 5.8.
EC Y(s) U(s) I(s) HF(s) HRE(s) P(s)

Fig. 5.8.
In acest caz, ![]()
H 0(s) = [ Il + HF(s) HRE(s) ]-1 HF(s). (5.26)
de unde rezulta
[ Il + HF(s) HRE(s) ] H 0(s) = HF(s) (5.27)
sau
HF(s) HRE(s) H 0(s) = HF(s) - H 0(s). (5.28)
Pentru l ≠ q, relatia (5.28) conduce la un sistem cu lq ecuatii din care rezulta elementele matricei HRE(s).
Pentru cazul particular l = q, din relatia (5.28), se obtine:
HRE(s) = [H 0(s)]-1 - [HF(s)]-1. (5.29)
5.5.2. Sisteme automate multivariabile autonome
Cand l=q, un obiectiv important al proiectarii sistemelor automate multivariabile este acela de a realiza un sistem multivariabil autonom adica un sistem la care fiecare marime de intrare influenteaza valorile unei singure marimi de iesire, fara a avea vreo influenta asupra celorlalte marimi de iesire.
Printr-o asemenea proiectare, se asigura decuplarea canalelor fie in raport cu marimile de intrare, fie in raport cu marimile perturbatoare. De remarcat faptul ca nu se pote realiza decuplarea canalelor atat in raport cu marimile de intrare, cat si in raport cu marimile perturbatoare
In cazul unui sistemautomat multivariabil autonom decuplt in raport cu intrarile H 0(s) este o matrice diagonala de forma:
H 0(s)

Exprimand iesirile functie de intrari, se obtine

5.5.3. Exemplu de sinteza a unui sistem automat multivariabil autonom
Pentru un sistem automat multivariabil cu doua intrari si doua iesiri, adica l=q=2, partea fixata F are structura din fig.5.3. Se considera:
![]()
![]()
![]()
![]()
rezulta ca matricea partii fixate este:
HF(s)

Se doreste obtinerea unui sistem automat multivariabil autonom, adica pentru H 0(s) se impune o forma diagonala unde:
![]()
![]()
deci
H 0(s)

Proiectarea se realizeaza in conformitate cu varianta a), prezentata in cadrul paragrafului 5.4.1. Conform relatiei (5.21), rezulta:
HRI (s) = [HF(s)]-1 H 0(s) [ I2 - H 0(s) ]-1. (5.34)
Din relatia (5.32), rezulta determinantul matricei partii fixate
det [HF(s)]
![]()
transpusa
[HF(s)]T

adjuncta
[HF(s)]*

si inversa acesteia
[HF(s)]-1

Cum
I2 - H 0(s)

rezulta
[I2 - H 0(s)]-1

Inlocuind matricele (5.38) (5.33) si (5.40) in relatia (5.34), se obtine matricea:
HRI (s)

de unde rezulta ca blocul regulatoarelor este forma din patru regulatoare, de tip PI, cu functiile de transfer:
![]()
![]()
![]()
![]()
Tinand cont de structurile reprezentate in figurile 5.3 si 5.6, pentru sistemul automat multivariabil proiectat, se obtine schema bloc din fig. 5.9.
HF HF HF HF + + + + u u y y F HRI HRI HRI HRI + + + + RI + + i i EC

Fig. 5.9.
5.6. Controlabilitatea si observabilitatea sistemelor dinamice liniare multivariabile
5.6.1. Metoda variabilelor de stare aplicata sistemelor multivariabile
In cazul sistemelor multivariabile, metoda variabilelor de stare este foarte avantajoasa deoarece permite descrierea matematica a comportarii sistemelor prin intermediul relatiilor matriceal-vectoriale.
Considerand un sistem multivariabil cu q intrari si l iesiri, in urma alegerii variabilelor de stare, rezulta un sistem matriceal-vectorial de forma:
![]()
unde:
x(t) - vectorul de stare (dimensiune n);
u(t) - vectorul de intrare (dimensiune q);
y(t) - vectorul de iesire (dimensiune l);
A - matricea sistemului (dimensiune n x n);
B - matricea intrarii (dimensiune n x q);
C - matricea iesirii (dimensiune l x n);
D - matricea conexiunii directe (dimensiune l x q).
Sistemul (5.42) a fost rezolvat in cadrul paragrafului 3.4.1.2, unde s-au obtinut rezultatele:
![]()
![]()
unde
![]()
este matrice de tranzitie.
6. Sisteme automate neliniare
6.1. Generalitati
Un sistem este neliniar daca contine cel putin un element neliniar.
In realitate, elemente perfect liniare nu exista. Totusi unele elemente prezinta neliniaritati care pot fi neglijate. Este cazul neliniaritatilor neesentiale (liniarizabile), a caror influenta este nesemnificativa. In asemenea cazuri, elementele pot fi inlocuite prin modelele lor liniare.
Exista insa si cazuri in care neliniaritatile existente in cadrul unui element nu pot fi neglijate, deoarece acceptarea unui model liniar ar conduce la erori grosolane. Este cazul neliniaritatilor esentiale (neliniarizabile) si elementul trebuie considerat neliniar.
Sistemele automate neliniare pe langa elemente neliniare contin si elemente liniare. Schema bloc a unui sistem automat neliniar, ce contine un singur element liniar, este reprezentata in fig.6.1, unde cu EN s-a notat elementul neliniar, iar cu BL s-a notat blocul elementelor liniare.
BL EN u y i EC

Fig. 6.1.
Intr-un sistem neliniaritatile pot fi:
inerente - cand sunt determinate de caracteristicile reale ale elementelor sau
introduse intentionat - cand introducerea lor este voita, in scopul imbunatatirii performantelor sistemului.
Sistemelor neliniare nu li se pot aplica aceleasi metode de studiu, ca sistemelor liniare. Nu se mai poate aplica metoda suprapunerii efectelor, nu este permisa extrapolarea, nu este permisa descompunerea semnalelor. Semnalele trebuie interpretate global.
Comportarea unui sistem neliniar depinde in mod esential de conditiile initiale, de forma semnalului de intrare si de amplitudinea acestuia.
6.1. Principalele tipuri de neliniaritati intalnite in practica
In acest paragraf, pentru principalele tipuri de elemente neliniare intalnite in practica, se vor prezenta grafic si analitic caracteristicile acestora.
Daca se noteaza u marimea de intrare a unui element neliniar (EN) si cu y marimea de iesire a
acestuia, caracteristica elementului neliniar (liniarizata pe
portiuni) este data de dependenta:
![]()
Principalele tipuri de elemente neliniare intalnite in practica sunt urmatoarele:
a) EN cu caracteristica tip releu bipozitional (fig. 6.2)
u y -M M u y M -M a -a u y M -M a -a


Fig. 6.2.
b) EN cu caracteristica tip releu tripozitional (fig. 6.3)

Fig. 6.3.
c) EN cu saturatie (fig. 6.4)

Fig. 6.4.
u y a -a k=tg(α)
 d)
EN cu zona de insensibilitate
(fig. 6.5)
d)
EN cu zona de insensibilitate
(fig. 6.5)

Fig. 6.5.
e) EN cu zona de insensibilitate si saturatie (fig. 6.6)
k=tg(α) u y a b -b -a -M M


Fig. 6.6.
f) EN cu caracteristica tip releu bipozitional si histerezis (fig. 6.7)
u y M -M -a a


Fig. 6.7.
g) EN cu caracteristica tip releu tripozitional si histerezis (fig. 6.8)
u -M M -a a b -b y


Fig. 6.8.
h) EN cu saturatie si histerezis (fig. 6.9)
u y a b -b -a -M M k=tg(α)


Fig. 6.9.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2758
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved