TEHNICI DE IMPLEMENTARE A TIPULUI DE DATE ABSTRACT (TDA) GRAF

TEHNICI DE IMPLEMENTARE A TIPULUI

DE DATE ABSTRACT (TDA) GRAF

In vederea prelucrarii grafurilor, concepute ca si tipuri de date abstracte (TDA) cu ajutorul sistemelor de calcul, este necesara in primul rand stabilirea modului lor de reprezentare. Aceasta activitate consta de fapt in desemnarea unei structuri de date concrete care sa materializeze in situatia respectiva tipul de date abstract graf.

In continuare sunt prezentate mai multe posibilitati de implementare a unui TDA-graf, alegerea depinzand atat de natura grafului de implementat,cat si de natura operatiilor care se executa asupra lor.

2.1.Implementarea grafurilor prin matrice de adiacenta

Cel mai direct mod de reprezentare al unui tip de date abstract graf il constituie matricea de adiacenta (adjacency matrix). Considerand graful G=(N,A) si multimea nodurilor sale N=, atunci matricea de adiacenta este o matrice A[n][n] de elemente intregi, unde A[x][y] este TRUE (1) daca si numai daca exista un arc de la nodul x la nodul y.

Primul pas in reprezentarea unui graf prin matrice de adiacenta consta in stabilirea unei corespondente intre numele nodurilor si multimea indicilor.

Aceasta corespondenta poate fi realizata in mod implicit prin alegerea corespunzatoare a

tipului de baza al multimii N sau in mod explicit prin precizarea unei asocieri definita pe multimea nodurilor cu valori in multimea indicilor intregi. In cazul corespondentei implicite cel mai simplu mod de implementare consta in "a denumi" nodurile cu numere intregi care coincid cu indicii de acces in matricea de adiacenta. Numele nodurilor pot fi deasemenea litere consecutive ale alfabetului sau, in cazul limbajului C constante ale unui tip enumerare definit de utilizator, in ambele cazuri existand posibilitatea conversiei directe a tipurilor respective in tipul intreg prin functii specifice de limbaj.

In cel de-al doilea caz, pentru implementarea asocierii pot fi utilizate tehnici specifice simple cum ar fi cele bazate pe tablouri sau liste sau tehnici mai sofisticate bazate spre exemplu pe arbori binari sau pe metoda dispersiei.

Pentru o urmarire usoara a algoritmilor vom utiliza o metoda implicita conform careia nodurile vor avea numele format dintr-o singura litera. In figura urmatoare apare reprezentarea bazata pe matrice de adiacente a grafului din figura 1.7:

A B C D E F G H I J K L M

Figura 2.1 - Reprezentarea grafului din figura 1.7 prin matrice de adiacenta

Se observa faptul ca reprezentarea are un caracter simetric intrucat fiind vorba de un graf neorientat arcul care conecteaza nodul i cu nodul j este reprezentat prin doua valori in matrice:A[i][j], respectiv A[j][i].

In astfel de situatii, deoarece matricea de adiacenta este simetrica ea poate fi memorata pe jumatate, acest lucru aducand pe langa avantaje si dezavantaje. Astfel, pe de-o parte limbajul C nu este propice unei astfel de implementari, iar pe de alta parte algoritmii care prelucreaza astfel de matrici sunt oarecum mai complicati decat cei care prelucreaza matricile integrale.

In prelucrarea grafurilor se poate face presupunerea ca un nod este conectat cu el insusi, lucru care se reflecta in valoarea TRUE memorata in toate elementele situate pe diagonala principala a matricei de adiacenta.

In continuare vor fi prezentate doua moduri de implementare a unui TDA-graf cu ajutorul matricilor de adiacente:

Metoda I: Dupa cum s-a precizat, un graf este definit prin multimea nodurilor si prin multimea arcelor sale. In vederea prelucrarii, un astfel de graf trebuie furnizat drept data de intrare algoritmului care realizeaza aceasta activitate. In acest scop este necesar a se preciza modul in care se vor introduce in memoria sistemului de calcul elementele celor doua multimi. O posibilitate in acest caz o reprezinta citirea directa, ca data de intrare, a matricei de adiacente, metoda care nu convine in cazul matricilor rare. O alta posibilitate o reprezinta citirea intr-o prima etapa a numelor nodurilor in vederea crearii asocierii anterior amintite, iar apoi in etapa urmatoare, a citirii perechilor de nume de noduri care definesc arce in cadrul grafului. Pornind de la acestea se genereaza matricea de adiacente.

Metoda II: Acest caz prezinta o metoda mai elaborata de implementare a unui TDA graf, utilizand drept suport limbajul " C ". Reprezentarea presupune definirea tipurilor si structurilor de date urmatoare:

Graful din figura 2.2 poate fi reprezentat in acest caz prin urmatoarele elemente: Contor care precizeaza numarul de noduri, Noduri - tabloul care pastreaza nodurile propriu-zise si Arce - matricea de adiacente a grafului.

Figura 2.2 - Structura unui TDA graf

In anumite situatii, pentru simplificare, nodurile nu contin alte informatii in afara cheii, caz in care TipElement=TipCheie. Alteori nodurile nu contin nici un fel de informatii (nici macar cheia), situatie in care intereseaza numai nodurile in vederea conectarii lor in cadrul reprezentarii.

Informatia in tabloul Noduri poate fi ordonata sau neordonata. In primul caz localizarea unei chei se poate realiza prin cautarea liniara.

Insertia unui nod depinde de asemenea de organizarea datelor. Daca acestea sunt neordonate, se incrementeaza g.Contor si se memoreaza elementul e in g.Noduri[g.Contor-1].

Considerand ca nodul nou introdus este izolat, vom introduce in matricea de adiacente g.Arce, pe linia g.Contor-1 si pe coloana g.Contor-1 valoarea FALSE.

In figura urmatoare este descrisa inserarea elementului E in graful din figura 2.2.

Figura 2.3 - Structura unui TDA graf dupa insertia unui nod

In cele ce urmeaza, pentru o urmarire usoara a operatiilor ce se vor efectua asupra structurii, vom considera ca TipEl coincide cu TipCheie.

Se vor folosi urmatoarele tipuri de date si variabile:

Functia care realizeza inserarea unui nod izolat intr-un TDA graf este urmatoarea:

Daca in tabloul Noduri informatiile sunt ordonate, atunci in prealabil, trebuie determinat locul in care se va realiza insertia, iar dupa aceasta trebuie realizate mutari de elmente atat in tabloul g.Noduri cat si in matricea de adiacente.

Intr-o maniera similara, la suprimarea nodului cu indexul indiceNod trebuie efectuate miscari in tablourile g.Noduri si g.Arce si trebuie realizata incrementarea lui g.Contor. Figura 2.4 ilustreaza suprimarea nodului B din structura de graf din figura 2.2. In vederea suprimarii, indiceNod are valoarea 1, precizand nodul B, iar suprimarea propriu-zisa presupune stergerea nodului din g.Noduri si modificarea matricei de adiacente prin excluderea arcului (B,D). Deoarece tabloul g.Noduri este neordonat, stergerea lui B se poate realiza prin mutarea ultimului element al tabloului in locul sau. Pentru pastrarea corectitudinii reprezentarii este necesara stergerea arcelor conexe lui B din lista de adiacente. Pentru aceasta se copiaza linia si coloana corespunzatoare ultimului nod din matricea g.Arce peste linia si coloana nodului B care a fost suprimat. In final se incrementeaza variabila g.Contor.

Figura 2.4 - Structura unui TDA graf dupa suprimarea unui nod

Functia care implementeaza aceste activitati este urmatoarea:

Daca tabloul Noduri este sortat, atunci suprimarea presupune mutarea cu o pozitie a tuturor nodurilor care au indexul mai mare ca IndiceNod din tabloul Noduri, precum si a liniilor si coloanelor corespunzatoare lor din matricea de adiacente. Se decrementeaza apoi contorul g.Contor.

Suprimarea unui nod presupune implicit si suprimarea arcelor conexe lui. Exista posibilitatea de a sterge arce fara a modifica multimea nodurilor. In acest scop se utilizeaza functia SuprimArc(g, indiceArc)

Datorita simetriei reprezentarii, stergerea unui arc presupune doua modificari in matricea de adiacente.

In figura 2.5 este precizata suprimarea arcului (BD) din graful figura 2.2.

Figura 2.5 - Suprimarea unui arc dintr-o structura de graf

Functia care realizeaza inserarea unui arc intr-un TDA graf este urmatoarea:

In concluzie, in cazul II de reprezentare, crearea unei structuri pentru un TDA graf presupune doua etape:

1.-precizarea nodurilor grafului, implementata printr-o suita de apeluri ale functiei InserNod (cate un apel pentru fiecare nod al grafului);

2.-conectarea nodurilor grafului, implementata printr-o suita de apeluri ale functiei InserArc (cate un apel pentru fiecare arc al grafului).

Atunci cand multimea nodurilor este neordonata, pentru determinarea indicelui corespunzator unui nod precizat prin cheia sa - cheia, in multimea de adiacenta, se va utiliza functia CautaNod(g,cheia):

2.2.Implementarea grafurilor prin sturcturi de adiacente

O alta maniera de reprezentare a unui TDA graf o constituie structurile de adiacenta

( adjacency structures). In cadrul acestei reprezentari, fiecarui nod al grafului i se asociaza o lista de adiacente in care sunt inlantuite toate nodurile cu care acesta este conectat.

In continuare se prezinta doua metode pentru implementarea grafurilor cu ajutorul structurilor de adiacente.

Metoda I. Implementarea structurii de adiacente se bazeaza in acest caz pe liste simplu inlantuite. Listele sunt construite in maniera obisnuita, cu un nod fictiv z pe post de fanion,a carui inlantuire indica nodul insusi.

Inceputurile listelor de adiacente sunt pastrate intr-un tablou "Stradi" indexat prin intermediul nodurilor. Initial in acest tablou se introduc inlantuirile la nodurile fictive, urmand ca insertiile in liste sa fie "la inceputul listei". Adaugarea unui arc care conecteaza nodul x cu nodul y in cazul acestui mod de reprezentare presupune in cazul grafurilor neorientate insertia nodului x in lista de adiacente a lui y si insertia lui y in lista de adiacente a nodului x. Un exemplu de program care construieste o astfel de structura apare in secventa de mai jos:

Program StructuraDeAdiacente:

Se observa ca un arc oarecare (x,y) este evidentiat in doua locuri in cadrul structurii (atat in lista de adiacente a lui x, cat si in lista de adiacente a lui y ). Acest mod redundant de evidentiere isi dovedeste utilitatea in situatia in care se cere sa se determine intr-o maniera eficienta care sunt nodurile conectate de un anumit nod x.

Pentru acest mod de reprezentare conteaza ordinea in care sunt prezentate arcele (perechile de noduri) la intrare. Astfel, un acelasi graf poate fi reprezentat ca structura de adiacente in moduri diferite. Ordinea in care apar arcele in lista de adiacente afecteaza la randul ei ordinea in care arcele sunt prelucrate de catre algoritm. In functie de natura algoritmilor utilizati in prelucrare, aceasta ordine poate sa influenteze sau nu rezultatul prelucrarii.

Aceasta metoda necesita ca fiecare nod alocat sa contina un numar variabil de pointeri,depinzand de numarul de noduri cu care este adiacent.

In figura 2.6 apare reprezentarea grafica a structurii construite pornind de la graful din figura 1.7. Datele de intrare (arcele) au fost furnizate in urmatoarea ordine:

(A,G), (A,B), (A,C), (J,K), (H,J), (H,I), (E,D), (F,D), (L,M), (F,E), (A,F), (G,E).

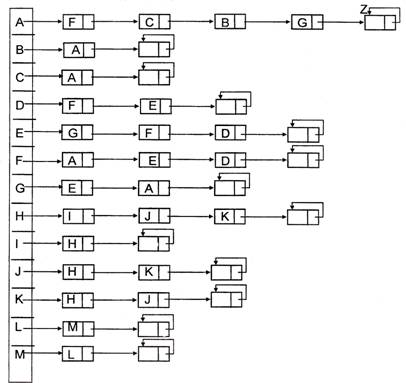
Figura 2.6 - Reprezentarea inlantuita(Metoda I)

Metoda II. O alta alternativa de implementare a structurilor de adiacente se bazeaza pe structuri multiinlantuite. Astfel, o structura de adiacente este de fapt o lista inlantuita a nodurilor grafului. Pentru fiecare nod al acestei liste se pastreaza o lista a arcelor, respectiv, o lista inlantuita a cheilor nodurilor adiacente. In consecinta, fiecare nod al listei nodurilor va contine doua inlantuiri, una indicand nodul urmator,cealalta, lista nodurilor adiacente.

In figura 2.7 apare reprezentarea schematica a unei structuri de adiacente:

Figura 2.7 - Reprezentarea schematica a unei structuri de adiacente

Secventa "C" care implementeaza structura multilista este urmatoarea:

Se face precizarea ca valorile aferente nodurilor sunt pastrate integral in lista de noduri. In lista de arce apar numai cheile. Desigur este posibil sa lipseasca campul "info" si deci TipElement=TipCheie.

In cadrul acestei structuri localizarea unui nod a carui cheie este cunoscuta se face utilizand tehnica cautarii liniare.

Insertia unui nod se va realiza simplu,la inceputul listei nodurilor.

Procedura InserArc(g,k1,k2) presupune insertia lui k1 in lista de adiacente a lui k2 si reciproc.Si in acest caz insertia se realizeza cel mai simplu la inceputul listei.

Suprimarea arcului precizat de indiceArc presupune extragerea a doua noduri din doua liste de adiacente diferite.Astfel,in figura 2.3, indiceArc contine doi pointeri v1 si v2, care indica doua noduri in lista de noduri.

In vederea suprimarii arcului care le conecteaza este necesar ca fiecare nod in parte sa fie suprimat din lista de adiacente a celuilalt. In cazul ilustrat, pentru a suprima arcul (A,C)=(C,A) se scoate A din lista lui C, respectiv C din lista lui A.

Procedura care realizeaza suprimarea arcului este urmatoarea:

Functia Cauta si procedura Suprima au fost realizate in termenii setului de operatori aplicabili obiectelor de tip lista.

Cauta(X,L) cauta nodul cu cheia X in lista de adiacente cu inceputul listei precizat de variabila pointer L si returneaza adresa nodului cu cheia X din aceasta lista.Daca X nu apare deloc returneaza pointerul nul:

Procedura Suprima(AX,LY) suprima nodul X de adresa AX, determinata prin procedura Cauta (prin cautarea nodului X in lista de adiacente a nodului Y), din lista de adiacente a nodului Y (cu inceputul marcat de variabila pointer LY).

Observatie: Apelul functiei se face din functia SuprimArc numai in cazul in care arcul exista.

Suprimarea unui nod dintr-o structura de tip graf presupune nu numai suprimarea propriu-zisa a nodului respectiv, ci si suprimarea tuturor arcelor incidente acestiu nod.