| CATEGORII DOCUMENTE |
O fibra optica este un ghid de unda dielectric cilindric realizat din materiale cu pierderi mici cum este sticla de siliciu SiO2. Fibra optica are un miez central (de raza a) in care se propaga lumina (Figura 1.1). Miezul este inconjurat de un strat cu indice de refracttie mai mic decat al miezului (de raza b). Intr-o astfel de fibra optica lumina poate fi ghidata cu pierderi foarte mici de doar 0, 16dB (≈ 3,6%).


Fig.1.1 Reprezentarea schematica a unei fibre optice
Daca diametrul miezului este mic atunci in fibra optica se poate propaga doar un singur mod (fibra se va numi fibra optica monomod). Pe masura ce diametrul fibrei se mareste se pot propaga din ce in ce mai multe moduri (fibra optica multimod).
Propagarea undelor in fibrele optice multimod presupune existenta unor diferente intre vitezele de grup ale diferitelor moduri. Acest lucru duce la largirea pulsurilor pe masura ce unda traverseaza fibra (efect numit dispersie modala) ceea ce limiteaza viteza de transmisie a comunicatiilor pe fibra optica.
 Dispersia modala poate fi redusa
prin utilizarea fibrelor optice cu gradient de indice de refractie astfel incat
are o valoare maxima in centrul miezului si este minim la margine
(Figura 1.2).
Dispersia modala poate fi redusa
prin utilizarea fibrelor optice cu gradient de indice de refractie astfel incat
are o valoare maxima in centrul miezului si este minim la margine
(Figura 1.2).
Fig. 1.2 (a) Fibra optica multimod cu salt de indice de refractie; (b) fibra optica monomod; (c) fibra optica cu gradient de indice de refractie
1.2 Fibre optice cu salt de indice de refractie
Astazi fibrele cu salt de indice de refractie se produc in geometrii standard pentru care raportul dintre diametrul miezului si a stratului exterior 2a/2b poate fi: 8/125, 50/125, 62.5/125, 85/125, 100/140 (valorile sunt trecute in mm). Indicii de refractie pentru miez n1 si pentru invelis n2 au valori apropiate astfel incat variatia relativa a acestor indici:
![]()
(1.1)
Fibrele optice cu salt de indice de refractie sunt realizate din sticla de siliciu SiO2
de puritate mare si variatia indicelui de refractie se realizeaza prin doparea sticlei cu Ti, Ge, boron cu diferite concentratii. Astfel: n1 = 1, 44 1, 46 functie de lungimea de unda folosita si Δ = 0, 001 0, 002.
Raze ghidate
Conditia de reflexie totala iın fibra optica θ > l = sin-1( n2/n1) pentru unghiuri de incidenta sau θ < θc < cos-1( n1/n2) pentru unghiurile complementare. Razele care se propaga intr-un plan meridional (plan care contine axa fibrei) raman incluse in acest plan fara schimbarea unghiului de incidenta (Figura 1.3) si cum n1 n2 rezulta ca θc are o valoare foarte mica incat toate razele ghidate de catre fibra in plan meridional sunt aproximativ paraxiale.


Fig. 1.3 Reflexia totala a
unei raze din planul meridional
O raza inclinata este identificata, poate fi descrisa prin planul de incidenta (paralel cu axa fibrei) care contine raza si unghiul pe care il face raza cu axa. Planul de incidenta intersecteaza marginile cilindrice dintre miez si invelis sub un unghi Φ cu normala la suprafata de marginire, la o distanta R fata de axa fibrei. Raza este identificata si de unghiul Φ cu axa fibrei. Cand Φ 0 (R ≠ 0) raza se numeste iınclinata spre deosebire de raza meridionala pentru care Φ=0 si R=0.
O raza inclinata se reflecta repetat in planele care fac unghiul Φ cu suprafata de separatie miez-iınvelis si urmeaza o traiectorie tip elice restransa intr-o patura cilindrica de raza interna R si externa a (Figura 1.4). Proiectia traiectoriei in planul (x - y) este un poligon regulat, nu neaparat iınchis. Se poate arata ca aceasta raza se reflecta total daca θ (unghiul format de raza cu axa z este mai mic decat θc)
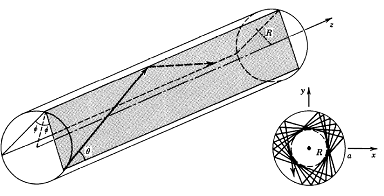
Fig. 1. 4 Propagarea unei raze inclinate intr-o fibra optica
Apertura numerica
O raza incidenta patrunde din aer intr-o fibra optica sub un unghi θa fata de normala la planul de incidenta. Se pune problema de a calcula cat de mare trebuie sa fie unghiul θa astfel incat raza refractata sa fie reflectata total in interiorul fibrei.
Conform legii Snell la suprafata aer-miez:

Am definit astfel apertura numerica a fibrei ca fiind sinusul unghiului de incidenta
maxim pe care il poate avea o raza cand patrunde din aer in miezul fibrei pentru ca mai apoi sa fie reflectata total (altfel spus, sa fie o raza ghidata de fibra). Atunci cand diferenta relativa a indicilor de refractie este mica se mai poate aproxima:
![]()
(1.2)
si unghiul θa se mai numeste si unghi de acceptare a fibrei (Figura 1.5)


Fig. 1.5. O unda este ghidata de catre fibra optica daca are un unghi de incidenta mai mic decat θa (unghiul de acceptare ce
determina in spatiu
un con de acceptare)
Apertura numerica descrie capacitatea fibrei de a ghida lumina. Trebuie mentionat si faptul ca razele de lumina refractate la capatul fibrei sunt cuprinse intr-un con cu deschiderea θa..
Undele ghidate
Undele ghidate sunt undele electromagnetice care satisfac conditiile de reflexie totala la interfata dintre miez si invelisul exterior al fibrei
Ca si in cazul modurilor de propagare intr-un ghid de unda dielectric rectangular si in cazul propagarii printr-o fibra optica atat intensitatea campului electric cat si intensitatea (sau inductia) campului magnetic satisfac ecuatia Helmholtz
![]()
unde cu U s-a notat unul din cei doi vectori ai campului electromagnetic si k0 =2πlλ0. Ecuatia este satisfacuta de caampul electromagnetic atat in miezul fibrei (unde n=n1 pentru r<a) cat si in invelis (in care n=n2 pentru r>a; se presupune ca raza iınvelisului b este suficient de mare). In coordonate cilindrice ecuatia Helmholtz se scrie:
![]()
(1.3)
cu U=U(r,Φ,z). Vom cauta solutiile ecuatiei de mai sus corespunzatoare undelor care se propaga pe directia z cu o valoare a constantei β. Din acest motiv solutia U o presupunem a fi de tip armonic pe directia z. Presupunem ca:
![]()
(1.4)
si introducand aceasta functie in ecuatia (1.3) rezulta:

(1.5)
Undele sunt ghidate atunci n2k0 < β <n1k0 si se definesc marimile:
 (1.6)
(1.6)
(1.7)
cu alte cuvinte, undele sunt ghidate de fibra atunci cand
![]()

si in invelisul miezului:

Ecuatiile (1.8) si (1.9) au ca solutii nebanale si marginite functii de tip Bessel:

unde Jl(x) sunt functiile Bessel de speta I de ordin l; Kl(x) sunt func'ii Bessel modificate de ordin l (functii Bessel de speta II).
Functia Jl(x) oscileaza ca un sin sau cos atenuat pentru x 1:
![]()
iar Kl(x) descreste exponential cu x pentru x 1:
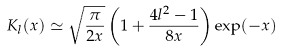

Fig. 1.6 Functiile Bessel pentru 2 moduri de propagare: (a) l=0 si (b) l=3
Cele doua
functii sunt reprezentate in Figura 1.6 Cei doi parametri kT
si γ determina profilul radial al caampului
electromagnetic. Astfel, o valoare mare pentru kT inseamna o variatie
periodica mai rapida a distributiei campului in miez, in timp ce
o valoare mare pentru determina
o scadere mai rapida a campului undei in invelis. Din definitiile
celor doi parametri (1.6) si (1.7) se observa ca suma patratelor
celor doi parametri este o
![]()
(1.13)
astfel incat atunci cand kT creste scade si campul va patrunde mai adanc in iınvelis, iar pentru kT > NA*k0 si < 0 si unda inceteaza sa se propage doar in limitele miezului (dispare reflexia totala).
Parametrul fibrei V
Se pot defini doi parametri X si Y adimensionali conform relatiilor:
X=kTa; Y= γa (1.14)
si intre cei doi parametri este valabila relatia:
X2+Y2=V2 ( .15)
 unde V=NA*k0a:
unde V=NA*k0a:
(1.16)
este un parametru important de care depinde numarul de moduri pentru fibra optica si constantele lor de propagare. Acest parametru se numeste parametrul fibrei sau, mai scurt, parametrul V. O unda electromagnetica este ghidata de catre fibra optica daca X<V.
Moduri de propagare
Modurile de propagare sunt determinate de constantele de propagare conform relatiei de dispersie (sau ecuatie caracteristica˘) β= β(a/λ0,n1,n2). Pentru determinarea modurilor de propagare se impun conditiile de continuitate pentru fiecare unda in punctele in care r=a (la interfata miez-invelis). Vor rezulta astfel constantele de propagare ce vor depinde si de ordinul l al functiilor Bessel: βlm. In acest fel modurile de propagare sunt sunt descrise de l si m: numere care vor descrie distributia radiala si azimutala (de exemplu, l=0 descrie propagarea undelor meridionale). In plus, fiecarei perechi de numere l,m va fi caracterizata si de 2 stari independente de polarizare pentru vectorii E si H.
Ecuatia caracteristica pentru o fibra cu ghidare slaba
Marea majoritate a fibrelor optice sunt fibre denumite cu ghidare slaba pentru care Δ 1 ceea ce determina ca doar razele paraxiale sa fie ghidate de catre aceste fibre. In acest caz componentele longitudinale pentru intensitatea campului electric si magnetic au valori mult mai mici decat componentele transversale si unda este practic de tip transversal electromagnetic TEM. Un mod de propagare liniar polarizat pe o directie in planul (x, y) se noteaza LPlm Daca se impune conditia ca functia de distributie radiala a campului electromagnetic u(r) sa fie continua si cu derivata continua in punctele r = a din (1.8) si (1.9) rezulta:

(1.17)
unde Jl' si Kl' sunt derivatele functiilor Bessel care satisfac identitatile:

de aici se poate deduce ecuatia caracteristica:

si cum X si Y sunt legate prin relatia X2+Y2=V2 fiind date valorile pentruV si l rezulta ca ecuatia caracteristica (1.18) este o ecuatie de o singur˘a variabila X.
Radacinile acestei ecuatii determina modurile de propagare. Se mai observa ca ecuatia de mai sus ramane neschimbata daca se schimba semnul pentru l deoarece J-l(x)= (-1)lJl(x) si K-l(x)= Kl(x). Ecuatia (1.18) are solutii care pot fi aflate grafic. Solutiile sunt reprezentate de intersectiile iıntre graficele celor doua functii (Figura 1.7). Se afla astfel solutii Xlm cu m = 1, 2, . . . , Ml si corespunzator se vor gasi valori pentru kTlm, γlm si constantele de propagare βlm corespunzaatoare.
 Fiecare mod are o distributie
radiala distincta. De exemplu: LP01(l =0, m =1) pentru V =
5 si LP34 34 (l =
3, m = 4) pentru V = 25 sunt moduri reprezentate in Figura
1.6.
Fiecare mod are o distributie
radiala distincta. De exemplu: LP01(l =0, m =1) pentru V =
5 si LP34 34 (l =
3, m = 4) pentru V = 25 sunt moduri reprezentate in Figura
1.6.
Figura 1.7 Solutia grafica a ecuatiei caracteristice
 Cum modurile (l,m) si (-l,m) sunt moduri care au aceeasi constanta de propagare
este interesant sa se analizeze distributia spatiala a
superpozitiei acestor unde: amplitudinea complexa a sumei este proportionala
cu ulm(r) cos(lΦ) exp(-jβlmz)
si intensitatea este proportionala cu
Cum modurile (l,m) si (-l,m) sunt moduri care au aceeasi constanta de propagare
este interesant sa se analizeze distributia spatiala a
superpozitiei acestor unde: amplitudinea complexa a sumei este proportionala
cu ulm(r) cos(lΦ) exp(-jβlmz)
si intensitatea este proportionala cu
![]()
Figura 1.8 Distributiile
radiale ale intensitatilor
pentru modurile: (a) LP01 si
(b) LP34
Taierea modurilor si numarul de moduri
Este evident din Figura 1.7 ca pe masura ce parametrul V creste va creste si numarul de moduri (date de intersectiile celor doua curbe) pentru ca in ecuatia caracteristica (1.18) membrul stang nu depinde de V, iar membrul drept se extinde spre dreapta cand V creste. Considerand semnele minus in ecuatia caracteristica (1.18) rezulta o intersectie a membrului stang din ecuatie cu axa X pentru Jl-1(x)= 0. Aceste radacini vor fi notate cu Xlm cu m = 1, 2, . . .. Numarul de moduri pentru acelasi l este egal cu numarul de radacini pentru functia Jl-1(x). Din acest motiv numarul de moduri Ml < V. Modul (l,m) este permis daca V=Xlm. Daca V descreste atunci modul (l,m-1) isi poate atinge punctul de
taiere s.a.m.d. Cea mai mica radacina pentru Jl-1(x). este X01 = 0 pentru l = 0 si urmatoarea valoare X11 = 2, 405 pentru l = 1. Atunci cand V < 2, 405 toate modurile cu exceptia modului fundamental LP01 sunt taiate (nu se pot propaga). Fibra optic va functiona doar ca un ghid monomod. O reprezentare a numarului de moduri Ml functie de V este de tip scara si creste cu o unitate atunci cand se ajunge la fiecare radacina Xlm a functiei Bessel Jl-1(x). (vezi tabelul 1.1
|
l/m | |||
Tabelul 1.1 Parametrii de taiere
Pentru modurile LPom si LP1m
Daca se numara toate modurile posibile M indiferent de valoarea l se obtine o variatie functie de parametrul V ca in Figura 1.9. In acest grafic este de tip scara cu salturi la fiecare radacina pentru Jl-1(x). La fiecare radacina se adauga cate doua moduri deoarece pentru fiecare l > 0 se gaseste si modul -l identic cu exceptia faptului ca se schimba semnul unghiului Φ (modul acesta corespunde razelor cu traiectorie elicoidala dar de sens opus). In plus, fiecarui mod i se asociaza cate 2 stari de polarizare.

|
Numar de moduri M |
Numarul de moduri (pentru fibre cu V mare
Pentru fibrele cu V mare, functia Jl1(x) are un numar mare de radacini in intervalul 0<X<V. Atunci cand X 1 functia Bessel poate fi aproximata de o functie sinusoidala si radacinile de taiere Xlm sunt aproximate de relatia:

(1.19)
Pentru o valoare l fixata
distanta dintre doua radacini consecutive este p astfel
incat numarul de radacini Ml satisface
relatia (l + 2Ml)π/2 = V de unde Ml ≈
V/π - l/2. Deci Ml descre;te liniar cu l (Figura 1.10)
incepand de la valoarea
V/π pentru l = 0 si terminand cu Ml =
0 caand l = lmax unde . l = lmax = 2 V/π. Numarul
total de moduri este:
![]()
 (
(
(1.20)
unde 4 este datorat starilor de polarizare si solutiilor simetrice.

Figura 1.10 Numarul de moduri intr-o fibra
cu V mare este aproximat de aria triunghiului determinat de legatura intre l, m si parametrul fibrei optice V.
Constantele de propagare fibre optice cu V mare
Constantele de propagare se determina din ecuatta
caracteristica (1.18) pentru fiecare solutie Xlm de
unde
![]()
Pentru V1, cea mai drastica aproximare pentru calculul constantelor de propagare presupune ca Xlm au valori egale cu valorile de taiere a modurilor xlm. Aceasta este echivalent cu a presupune ca ramurile din Figura 1.7 sunt aproximate de drepte verticale incat Xlm = xlm. Cum V1, numarul de radacini este mare si se pot folosi aproximatiile deduse pentru xlm si:
![]()
cum:
![]()
rezulta:
![]()
Deoarece Δ are o valoare mica se utilizeaza aproximarea (1 + δ)1/2 ≈ 1 + δ/2 pentru | δ| 1 se obtine relatia aproximativa pentru constantele de propagare:

Cum l+2m variaza intre 2 si ≈
2V/ =
![]()
![]()
Vitezele de grup (fibre cu V mare)
Pentru a determina viteza de grup vlm = dω/dβlm va exprima constantele de propagare βlm explicit functie de ω prin
substitutia n1k0 = ω/c1 si
![]()

Deoarece valorile minime si maxime pentru l+2m
sunt 2 si
![]()

Figura 1.11 (a) Constantele aproximative pnetru βlm la o fibra cu V mare functie de l, m
(b)
Fibre monomod
Asa cum am mai amintit, o fibra cu raza miezului a si apertura numerica NA functioneaza ca o fibra monomod in modul fundamental LP01 daca V =2π (a/λ )NA <2.405 Altfel spus, fibra este monomod daca are diametrul miezului mic si are o apertura numerica mica (cu n2 apropiat de n1). Modul fundamental are o distributie spatiala Gaussiana si este modul care confineaza cel mai mult puterea undei electromagnetice in miezul fibrei. Se pot enumera o serie de avantaje pentru fibrele monomod atunci cand sunt utilizate in comunicatii. Astfel, diferite moduri au viteze de grup diferite si determina aparitia unei intarzieri a semnalului incat pulsurile de lumina au o imprastiere in timp (se largesc). Pe de alta parte, in fibrele optice monomod aceasta imprastiere in timp este mult mai mica decat in cazul fibrelor modale. Un alt dezavantaj al fibrelor multimod consta in interferenta aleatorie a modurilor si se obtine un asa numit zgomot modal. Fenomenul este asemanator pierderii in claritate a semnalului radio datorita cailor multiple de transmisie (interferenta distructiva intre doi transmitatori). In fibra monomod unda se transmite pe o singura cale fara zgomot modal. Datorita marimilor mici si a aperturilor numerice mici fibrele optice monomod sunt excelente pentru integrarea cu tehnologia optoelectronica. Totusi, acelasi lucru face ca fibrele monomod sunt mai fragile mai ales la imbinarile cu partile electronice ale retelelor de comunicatii.
Schimbarea polarizarii in fibrele optice monomod
Intr-o fibra optica cu sectiune transversala
circulara, fiecare mod se poate propaga cu doua saari de
polarizare distincte cu aceeasi

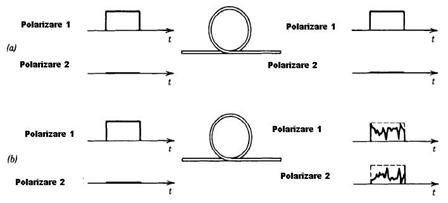
Figura 1.12
(a) Fibra ideala
(b) Cuplajul aleator intre polarizarile undelor
Daca ne intereseaza doar puterea totala transmisa prin fibra acest fenomen de schimbare aleatorie a polarizarii nu pune probleme datorita faptului ca este inregistrata doar puterea totala transmisa prin fibra.
In alte domenii de utilizare a fibrelor optice, de exemplu in comunicatiile optice coerente, dispozitive optice integrate, senzori optici bazati pe tehnici de interferometrie, trebuie mentinuta starea de polarizare a luminii si se va evita folosirea fibrelor optice cu sectiune circulara. In aceste cazuri se utilizeaza de obicei fibre cu sectiune transversala eliptica sau in care au fost induse anizotropii ai indicelui de refractie pentru eliminarea degenerarii starii de polarizare.
1.3 Fibre optice cu gradient de indice de refractie
Obtinerea fibrelor optice cu gradient de indice de refractie a permis reducerea imprastierii pulsului datorita faptului ca diferitelor moduri de propagare prin fibra multimod le corespund viteze de grup diferite. Miezul unei astfel de fibre optice are un indice de refractie care variaza radial fiind maxim in centrul fibrei si descreste pana la o valoare corespunzatoare indicelui de refractie al invelisului. Viteza de faza pentru propagarea undelor luminoase in acest caz este minima in centrul fibrei si creste gradual cu departarea de centru. Razele modului de propagare ce se apropie cel mai mult de axa fibrei se vor propaga pe drumul cel mai scurt cu viteza cea mai mica. Razele modului cel mai oblic se propaga pe distante mai lungi in marea majoritate a timpului intr-un mediu unde viteza de faza este mai mare. Ca o consecinta imediata diferentele intre timpii de propagare
si intre vitezele de grup pentru diferite moduri se reduc. Indicele de refractie al miezului fibrei optice n(r) are o valoare care depinde de pozitia radiala r iar indicele de refractie al invelisului este constant si egal cu n2 Valoarea maxima pentru n(r) este n(0) = n1 si pentru r = a rezulta n(a) = n2. (v. Figura 1.13)


Figura 1.13 Geometria si profilul indicelui de refractie pentru fibra optica cu gradient de indice de refractie
O functie care indeplineste conditiile de marginire de mai sus pentru profilul indicelui de refractie n(r) este functia putere de forma:
![]()
(1.26)
unde:
![]()
si p o marime numita gradul profilului indicelui de refractie ce defineste forma acestui profil. Astfel: pentru p = 1, n2(r) este o functie liniara de r; pentru p = 2 profilul este patratic etc. Daca p→ ∞ atunci n2(r) se apropie de functia treapta (v. Figura 1.14).


Figura 1.14 Profilul indicelui de refractie pentru o fibra optica pentru care n2(r) variaza ca o functie putere pentru diferite grade p.
Razele meridionale au traiectorii oscilatorii planare iar celelalte raze de lumina se propaga pe traiectorii elicoidale cu puncte de intoarcere ce determina doua suprafete cilindrice (v. Figura 1.15)


Figura 1.15 Raze ghidate in interiorul fibrei optice cu gradient de indice de refractie (a) raze meridionale;
(b) raze insurubate
Unde ghidate
Modurile fibrei cu gradient de indice de refractie pot fi determinate prin rezolvarea ecuatiei Helmholtz (1.3) cu n = n(r) astfel incat se obtin distributiile spatiale ale componentelor campului ce vor trebui sa satisfaca ecuatiile lui Maxwell cu conditiile de marginire in centrul fibrei si la interfata miez-invelis. Aceasta abordare este dificila, desi nu imposibila. Din acest motiv, se va utiliza o teorie aproximativa bazata pe reprezentarea distributiei de camp pentru o unda cuasiplana ce se propaga in miezul fibrei pe traiectoria unei raze optice ghidate. O unda cuasi-plana este o unda caracterizata la un moment dat si intr-un punct dat de aceeasi ecuatie ca si unda plana dar isi schimba directia de propagare si amplitudinea putin pe masura ce se propaga. Aceasta aproximatie ne permite sa utilizam notiuni de optica geometrica pentru determinarea constantelor de propagare pentru modurile ghidate iar metoda de calcul este denumita metoda WKB (Wentzel-Kramers-Brillouin) si se poate aplica doar fibrelor optice cu un numar mare de moduri (cu parametru V mare).
Unde cuasi plane
In modelul undelor cuasiplane se va considera solutia ecuatiei Helmholtz de tipul:
U(r) = a(r) exp [-jk0S(r)] (1.28)
 unde
a(r) si S(r) sunt functii reale de pozitie ce variaza
putin in comparatie cu lungimea de unda λ0 =
2π/k0. In
plus marimea S(r) satisface ecuatia eikonal in mod aproximativ:
unde
a(r) si S(r) sunt functii reale de pozitie ce variaza
putin in comparatie cu lungimea de unda λ0 =
2π/k0. In
plus marimea S(r) satisface ecuatia eikonal in mod aproximativ:
![]()
![]()
(1.29)
Frecventa spatiala locala a undei in directia radiala este data de derivata partiala a fazei k0S(r) in raport cu r:
kr = k0 ds/dr (1.30)
astfel incat (1.28) devine:
![]()
![]() si (1.29) permite calculul pentru
frecventa spatiala locala:
si (1.29) permite calculul pentru
frecventa spatiala locala:
(1.32)
Pentru a gasi semnificatia fizica a notiunii
de unda cuasiplana, in relatiile de mai sus vom defini: kф
= l/r incat exp(-jlф)
= exp(-j kфrф) si pentru kz = β gasim ca
![]()
 Figura 1.16 (a) Vectorul k=(kr,
kф, kz) in coordonate cilindrice
Figura 1.16 (a) Vectorul k=(kr,
kф, kz) in coordonate cilindrice
(b) unda cuasiplana
Pentru a
determina regiunea de propagare din miezul fibrei cu gradient de indice de
refractie trebuie impusa conditia ca frecventa spatiala
radiala kr sa aiba o valoare reala,
altfel spus:
![]()
![]()
![]()
. se reprezinta
![]()
. termenul l2/r2 este scazut rezultand curba cu linie intrerupta;
. valoarea lui
![]()
.
![]()
. se observa ca regiunea pentru care
![]()
![]()
(1.33)

Figura 1.17 Determinarea regiunii de propagare a undei cuasiplane in fibrele optice cu gradient de
indice de refractie.
In concluzie: unda cuasiplana care se propaga intr-o fibra optica cu gradient de indice de refractie se propaga intr-o regiune limitata in sectiune transversala de razele rl si Rl ca si in cazul razei elicoidale.
Rezultatele de mai sus pot fi generalizate si in cazul fibrelor cu salt de indice de refractie in care n(r) = n1 pentru r < a si n(r) = n2 pentru r > a. In acest caz o unda cuasiplana este ghidata in miez prin reflexia la interfata invelis-miez, r = a. Regiunea de confinare a razelor este rl < r < a (Figura 1.17b) unde:

(1.34)
In invelis
(r > a) si langa
centrul miezului (r < rl),
![]()
Modurile de propagare
Modurile de propagare ale fibrei cu gradient de indice de refractie sunt determinate
![]() prin
impunerea conditiei de reproducere a undei dupa un pas al elicei intre
rl, Rl si
retur. Lungimea traiectoriei pe directia azimutala corespunde unui unghi
la centru de 2π Lungimea radiala pentru o propagare pe elicea completa
trebuie sa corespunda unei variatii de faza multiplu de
2π:
prin
impunerea conditiei de reproducere a undei dupa un pas al elicei intre
rl, Rl si
retur. Lungimea traiectoriei pe directia azimutala corespunde unui unghi
la centru de 2π Lungimea radiala pentru o propagare pe elicea completa
trebuie sa corespunda unei variatii de faza multiplu de
2π:
(1.35)
Aceasta
conditie, analoaga conditiei de reproducere a undei pentru
ghidurile de unda plane corespunde unei ecuatii caracteristice din
care se pot calcula constantele de propagare βlm pentru
diferite moduri de propagare. In Figura 1.18 au fost marcate schematic valorile
pentru constantele de propagare si se observa ca pentru modul m
= 1

Figura 1.18 Constantele de propagare si regiunile de confinare a radiatiilor optice pentru diferite
moduri de propagare
Numarul maxim de moduri de propagare
Numarul total de moduri poate fi determinat prin
adunarea numarului de moduri Ml pentru l = 0, 1,
. . . , lmax. Notaam cu qβ numarul
de moduri cu o
![]()
(1.36)
unde rl si R sunt razele de confinare corespunzatoare
constantei de propagare β determinate din (1.33). In acest caz numarul
total de moduri avand
![]()
 unde
lmax(β) este valoarea maxim[ a lui l pentru care se obtine un mod marginit cu
constanta de propagare mai mare decat β, adica pentru care valoarea
maxima a functiei
unde
lmax(β) este valoarea maxim[ a lui l pentru care se obtine un mod marginit cu
constanta de propagare mai mare decat β, adica pentru care valoarea
maxima a functiei
![]()
(1.38)
Pentru fibrele cu un profil al indicelui de refractie de tip functie putere, inlocuim (1.26) iın (1.36) si rezultatul in (1.38) prin evaluarea integralei se obtine:

(1.39)
![]() in care:
in care:
(1.40)
Aici
![]()
![]()
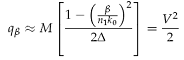
(1.41)
Constantele si vitezele de propagare
Constantele de propagare

(2.42)
Deoarece diferenta relativa a indicilor de refracie Δ are o valoare mica incat Δ 1 se poate folosi formula aproximativa pentru puterea unui binom (1 + δ)1/2 δ/2 si din formula (1.42) se obtine o formula aproximativa pentru calculul constantei de propagare:
![]()
(1.43)
Se observa ca βq scade de la o valoare de aproximativ n1k0
(pentru q = 1) pana la n2k0 (pentru q =
M) ca si in Figura 1.19. Pentru fibrele optice cu salt de indice de refractie
p → ∞
![]()
(1.44)


|
Constanta de propagare βq |
|
Constanta de propagare βq |
Figura 1.19 Dependenta constantelor de propagare βq de ordinul modului de propagare q = 1, 2, . . . ,M.
Vitezele de grup
![]() Pentru
a determina viteza de grup pentru un anumit mod de propagare
Pentru
a determina viteza de grup pentru un anumit mod de propagare
![]()
![]()
(1.45)
pentru fibra optica cu salt de indice de refractie p → ∞ si viteza de grup se poate calcula astfel:
![]()
cand viteza de grup variaza de la c1 pana la c1(1 - Δ), rezultat identic cu cel obtinut in relatia (1.25).
Profilul optim pentru indicele de refractie
Din relatia (1.45) se poate deduce ca
pentru p = 2 viteza de grup a radiatiilor ce se propaga prin
fibra optica este

si viteza de grup variaza de la c1 pana la c1(1 - /2) la q = M. In comparatie cu fibra optica cu salt de indice de refractie, pentru care viteza de grup variaza in intervalul c1 si c1(1 - ), fibra cu gradient de indice de refractie de profil parabolic are o variatie relativa a vitezei de grup proportionala cu Δ2/2 (Figura 1.20). In conditii ideale fibra optica cu gradient de indice de refractie reduce diferentele de viteze de grup cu un factor Δ /2 astfel incat dispersia modala fata de fibra cu salt de indice de refractie se micsoreaza simtitor.
|
Viteza de grup vq |
|
Viteza de grup vq |

 Figura 1. 20 Vitezele de grup pentru o fibra cu salt de indice de refractie
Figura 1. 20 Vitezele de grup pentru o fibra cu salt de indice de refractie
p → ∞ si pentru o fibra cu gradient optim de indice de refractie p = 2
Cum toata analiza de mai sus s-a facut pe baza unor aproximatii factorul Δ /2 nu este atins in practica. Mai mult, pentru p = 2 numarul de moduri M de propagare prin fibra cu gradient de indice de refractie este:
![]()
unde V = 2π(a/λ0)NA. Acest numar este egal doar cu o jumatate din numarul de moduri de propagare pentru o fibra cu salt de indice de refractie cu aceeasi parametr n1, n2 si a.
1.4 Atenuarea si dispersia
Atenuarea si dispersia sunt cele doua fenomene fizice care limiteaza performantele fibrelor optice si a canalelor de transmisie de date. Atenuarea limiteaza marimea puterii optice transmise iar dispersia limiteaza rata de transmisie a datelor deoarece determina imprastierea temporala a pulsurilor de date.
Coeficientul de atenuare
Unda luminoasa care se propaga prin fibra optica are o valoare a puterii ce scade exponential cu distanta de propagare datorita absorbtiei si a imprastierii. Coeficientul de atenuare a este de obicei definit in unitati dB/Km:
![]()
unde
![]()

(1.50)
cu α masurat in dB/km.

Figura 1.21 Relatia intre T si
coeficientul de transmisie α
masurat in dB
Daca coeficientul de atenuare α este exprimat in km-1 atunci:
![]()
ce exprima legea clasica a atenuarii. Pentru ca in comunicatiile prin fibra optica α se exprima in dB/Km raporul puterilor este definit de relatia (1.50).
Absorbtia
Coeficientul de absorbtie al sticlei de Si (SiO2) depinde puternic de lungimea de unda. Acest material are doua benzi de absorbtie puternica: in IR mijlociu datorita tranzitiilor de vibratie si in UV datorita tranzitiilor electronice si moleculare. Intre cele doua benzi de absorbtie se formeaza fereastra de transmisie ce ocupa regiunea corespunzatoare IR apropiat
Imprastierea
Imprastierea Rayleigh este un alt
efect intrinsec ce contribuie la atenuarea puterii luminoase transmise prin
fibra optica. Acest fenomen se datoreaza centrelor de imprastiere
din fibra formate prin variatia aleatoare a pozitiei unor atomi in
cristalul de oxid de siliciu. Amplitudinea campului imprastiat este
proportionala cu ω4 sau
![]()
![]()
Fereastra transparenta a sticlei de siliciu va fi marginita de imprastierea Rayleigh catre lungimile de unda scurte si de absorbtia IR la lungimi de unda mari.
.
Efecte extrinseci
Fata de efectele de limitare prezentate mai sus in fibrele optice folosite in comunicatii se mai manifesta si efecte extrinseci legate de absorbtia moleculelor de impuritati, in special de benzile de vibratie ale radicalului OH asociat cu vaporii de apa si cu impuritatile de ioni metalici. Progresele tehnologice in realizarea fibrelor optice de sticla au facut posibila eliminarea impuritatilor metalice dar impuritatile de OH sunt mai greu de eliminat. Lungimile de unda utilizate in mod curent pentru transmiterea informatiilor prin fibre optice sunt astfel selectate pentru a evita aceste benzi de absorbtie. Pierderile prin imprastierea luminii pot fi accentuate si de materialele dopante introduse pentru realizarea gradientului de indice de refractie, de exemplu.
Coeficientul de atenuare a radiatiei luminoase ghidate in fibrele de sticla depind absorbtia si imprastierea in miezul si invelisul fibrelor. Cum fiecare mod este caracterizat de diferite distante de penetrare in invelis astfel incat razele parcurg diferite distante efective rezulta ca si coeficientul de atenuare este diferit functie de modul de propagare. In general coeficientul de atenuare are o valoare mai mare pentru modurile de ordin mare. Fibrele monomod au coeficienti de atenuare mai mici decat fibrele multimod (v. Figura 1.22). Pierderile sunt introduse deasemenea de variatiile aleatorii in geometria fibrei si de anumite indoiri ale fibrei.


|
Atenuarea α (dB km |
Figura 1.22 Variatia coeficientului de atenuare a radiatiei optice in firele de siliciu multimod si
monomod.
|
Lungimea de unda λ0 (μm) |
Dispersia radiatiilor optice prin fibrele optice
Atunci cand un puls scurt de energie luminoasa se propaga printr-o fibra optica energia este "dispersata" in timp astfel incat pulsul se imprastie intr-un interval de timp mai amre. In cazul fibrelor optice dispersia este data de 4 fenomene distincte: dispersia modala; dispersia de material; dispersia de ghid de unda si dispersia neliniara.
Dispersia modala
Dispersia modala se manifesta in cazul fibrelor multimod ca efect al vitezelor de grup diferite pentru diferite moduri. Un puls de lumina ce intra la z = 0 intr-o fibra optica ce suporta M moduri de propagare se imprastie in M pulsuri luminoase ce se propaga intr-un timp τq = L/vq pe o lungime L de fibra cu viteza de grup a modului q, vq si q = 1, , M
Daca vmin si vmac sunt vitezele de grup minima si maxima atunci pulsul receptionat se impastie intr-un interval de timp L/vmin - L/vmax. Cum modurile de propagare nu sunt excitate in general in proportii egale, forma finala a pulsului are un profil neted (v. Figura 1.23). O estimare a largimii pulsului este data de abaterea patratica medie denumita in acest caz raspuns temporal al fibrei optice:
![]()
Intr-o fibra optica cu salt de indice de refractie si numar mare de moduri: vmin ≈ c1(1 - δ) si vmax = c1. Cum in acest caz se poate folosi aproximatia (1 - )-1 ≈ 1 + timpul de raspuns al fibrei este:
![]()
 adica
este o fractie Δ/2 din
timpul de propagare L/c1.
adica
este o fractie Δ/2 din
timpul de propagare L/c1.
Figura 1.23 Imprastierea pulsurilor de lumina datorita dispersiei modale prin fibra optica
Dispersia modala este mult mai mica in fibrele optice cu gradient de indice de refractie decat pentru fibrele optice cu salt de indice deoarece vitezele de grup au valori mult mai apropiate. Pentru o fibra optica care are un profil optim de indice de refractie si cu un numar mare de moduri de propagare: vmax = c1 si vmin = c1(1 - Δ2/2) incat timpul de raspuns va fi:
![]()
Se observa ca aceasta valoare pentru timpul de raspuns este mai mica decat (1.52) cu un factor Δ/2.
Dispersia de material
Materialele din care sunt confectionate fibrele
optice, de exemplu sticla, sunt materiale optic dispersive astfel incat un puls
luminos ce se propaga intr-un mediu dispersiv de indice de refractie n
va avea o viteza de grup v = c0/N cu
![]()

de unde raspunsul temporal al fibrei datorita dispersiei de material va fi:
στ = |Dλ| σλL (1.54)
![]() unde:
unde:
(1.55)
este coeficientul de dispersie al materialului. Acest tip de dispersie se numeste dispersie de material.
Dependenta coeficientului de dispersie de lungimea de unda Dλ pentru o sticla de siliciu este reprezentata in Figura 1.24. Se observa ca la lungimi de unda mai mici decat 1, 3μm coeficientul de dispersie are valori negative astfel incat pachetele de unda cu lungimi de unda mai mari se propaga mai repede decat cele cu lungimi de unda mai mici.

|
Coeficientul de dispersie Dλ (ps/km - nm) |

Figura 1.24 Coeficientul de dispersie al sticlei de siliciu functie de lungimea de unda.
|
Lungimea de unda λ0 (μm) |
Dispersia ghidului de unda
S-a constatat ca vitezele de grup pentru diferite moduri de propagare in fibrele optice depind de lungimea de unda chiar daca dispersia de material este neglijabila. Aceasta dependenta este cunoscuta ca dispersia ghidului de unda si se datoreaza dependentei distributiei de camp in fibra optica de raportul dintre raza miezului fibrei si lungimea de unda (a/λ0). Daca acest raport este modificat, prin schimbarea lungimii de unda λ0, se modifica raportul dintre puterile optice din miez si invelis ducand la modificarea vitezei de grup a modului respectiv de propagare. Dispersia ghidului de unda este mai accentuata in fibrele optice monomod, in care nu se manifesta dispersia modala si la lungimi de unda pentru care dispersia de material este mica.
In absenta dispersiei de material V este direct proportional cu ω astfel incat:

(1.56)
![]() Largirea
pulsului asociata cu largirea spectrala a sursei σλ
este data de timpul de propagare L/v prin fibra de lungime L:
Largirea
pulsului asociata cu largirea spectrala a sursei σλ
este data de timpul de propagare L/v prin fibra de lungime L:
unde:

(1.58)
este coeficientul de dispersie in ghidul de unda. Substituind (1.56) in (1.58) se obtine:

(1.59)
Dispersia de material combinata cu dispersia de ghid de unda (Dispersia cromatica)
Dispersia cromatica poate fi determinata prin includerea dependentei de lungimea de unda a indicilor de refractie n1 si n2 si de aici pentru NA atunci cand se determina dβ/dω din ecuatia caracteristica. Desi, in general, dispersia de ghid de unda este mai slaba decat dispersia de material aceasta duce la deplasarea lungimii de unda pentru care dispersia totala cromatica este minima. Cum dispersia cromatica limiteaza performantele fibrelor monomod, fibre mai avansate pot reduce acest efect utilizand miezuri cu gradient de indice de refractie selectate astfel incat lungimea de unda λ pentru care dispersia ghidului de unda compenseaza dispersia materialului. Fibre cu dispersie deplasaa au fost realizate cu succes prin utilizarea unui miez cu indice de refractie ce variaza in trepte avand o raza redusa ca in Figura 1.25. Aceasta tehnica poate fi utilizata pentru modificarea lungimii de unda pentru care dispersia cromatica nu se mai manifesta de la 1, 3μm pana la 1, 55μm unde fibra optica are atenuarea ce mai mica. Mai facem observatia ca si procesul de realizare a fibrelor optice cu gradient de indice de refractie introduce pierderi datorita substantelor dopante. Au fost realizate si alte profile de fibre optice cu gradient de indice de refractie pentru care dispersia cromatica este nula la 2 lungimi de unda si este redusa pentru o lungime de unda situata intre cele doua valori. Aceste fibre optice sunt numite fibre cu dispersie plaa si au fost realizate prin utilizarea a 4 straturi cu gradient de indice de refractie (v. Figura 1.25b).
|
Coeficientul de dispersie |



Figura 1.25 Profie de indici de refractie si dependenta de lungimea de unda a coeficientului de dispersie de material (linie plina) si a dispersiei de ghid de unda (linie intrerupta) pentru (a) fibre cu dispersie deplasata si (b) fibre cu dispersie plata.
Dispersia de material combinata cu dispersia modala
Efectul dispersiei de material asupra largirii
pulsului in fibrele multimod poate fi determinat prin rezolvarea ecuatiei
de dispersie pentru constantele de propagare βq si determinarea vitezelor de
grup a modurilor

![]()

(1.60)
 unde:
unde:
este indicele de de refracte de grup a materialului din care este realizat miezul fibrei. Cu aceasta aproximare expresia (1.45) ramane aceeasi numai ca indicele de refractie n1 este inlocuit cu indicele de refractie de grup N1. Pentru o fibra cu salt de indice de refractie (p → ∞) vitezele de grup a modurilor variaza de la c0/N1 pana la c0 (1 - Δ)/N1 astfel incat timpul de raspuns este:
![]()
Dispersia neliniara
Atunci cand intensitatea luminoasa a radiatiei ce se propaga prin fibra optica este foarte mare, indicele de refractie al miezului fibrei depinde de valoarea intensitatii datorita unor efecte optice neliniare. Acest efect produce asa-numita dispersie neliniara a fibrei optice. Componentele undei cu intensitate mai mare determina o deplasare de faza diferita fata de celelalte componente ale pulsului de lumina astfel incat frecventa de oscilatie este modificata. Acest lucru determina o alterare a pulsului care, in anumite conditii, poate compensa dispersia de material si pulsul se poate propaga fara modificarea formei (sub forma unei unde de tip soliton).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4243
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved