| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Statistická analýza dat - Indexní analýza
Indexy mohou být:
Indexy se skládají ze dvou složek:
p intenzita (úroveň znaku) např. Průměrný přírůstek,
q extenzita (počet) např. Počet dělníků, prasat atd.
Rozlišují se jednotlivá období za která se ukazatele sledují:
Indexy stejnorodých ukazatelů
Pomocí indexů se vyjadřují změny množstí q a změny přírůstků p a využívají se následující vzorce:
Změna množství
Jednoduchý index ![]()
Celkový index
![]()
Změna přírůstků
Jednoduchý index ![]()
![]()
Celková změna přírůstků IPS
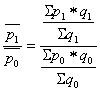
Odvozené indexy:
používají se když potřebujeme zjistit jak ovlivňují celkovou změnu přírůstku (apod) změny p či q.
Index stálého složení ISS
Zde se zjišťuje vliv změny p a q zůstává neměnné! Jelikož máme q0 a q1 tak můžeme napsat vzorec ve dvou formách a použijeme pro výpočet tu, která se nám víc hodí.
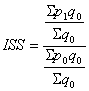
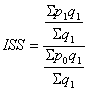
Index struktury IST
Zde se zjišťuje vliv změny množství q a p tedy zůstává neměnné! Také tady platí, že můžeme napsat vzorec pro oboje p.

Pozn. Z ISS a IST se dá zpětně vyjádřit vzorec pro průměr IPS. Veme se jeden ISS a jeden IST a vykrátí se qčka nebo pčka.
Příklady a jejich řešení
Jak postupovat, abychom nedělali chyby
základem je dobře si označit všechny proměnné, nemusíme mít jen p, q, ale také p*q, p/q a podobně
dobré je si do tabulky spočítat všechna čísla co budeme potřebovat a ta pak jen budeme dosazovat do jednotlivých vzorců, tím si ušetříme práci a také zabráníme tomu, abychom dělali více chyb (samozřejmě si musíme ty dílčí výsledky spočítat pečlivě, aby se nám pak případné chyby netáhly celým příkladem)
V ofiko materiálech je to př. č. 4
Ve třech podnicích zabývajících se výkrmem prasat v určité oblasti byla sledována
výše průměrného přírůstku v letech 2005 a 2006 :
|
Podnik |
Průměrný přírůstek na kus a den v kg |
Počet prasat ve výkrmu (ks) |
||
|
A | ||||
|
B | ||||
|
C | ||||
Určete :
a) jak se změnil celkový přírůstek v dané oblasti - IPS
b) jaký vliv na změnu celkového přírůstku měla změna počtu prasat v jednotlivých podnicích - IST
c) jaký vliv na změnu celkového přírůstku měla změna průměrného přírůstku v jednotlivých podnicích - ISS
d) jak se změnily počty prasat
e) jaká je změna průměrného přírůstku
ad A,
IPS. 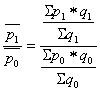 tedy
tedy  = 1,062
= 1,062
Přírůstek tedy změnil o 6%.
ad B,

Můžeme počítat podle obou vzorců s oběma p ale většinou se počítá s daty ze základního období, tedy s p0.
Výsledky:
IST s p0 = 1,003
IST s p1 = 1,004
Změna počtu prasat v jednotlivých podnicích by zapříčinila nárůst o 0,3%.
ad C,
Stejné jako B, akorát se mění p.
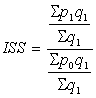 = 1,059
= 1,059  = 1,054
= 1,054
ad D,
změna počtu prasat. ![]() = 0,96
= 0,96
ad E,
změna
průměrného přírůstku … 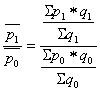 = 1,059
= 1,059
V ofiko materiálech je to př. č. 5
Na základě údajů o počtech pracovníků a mzdách ve třech dílnách v podniku v letech 2005 a 2006 vyjádřete, jaký vliv na změnu průměrné mzdy v podniku měla změna průměrných mezd v jednotlivých dílnách.
|
Dílna |
Počet pracovníků |
Měsíční objem vyplacených mezd |
Změna průměrné mzdy v roce 2006 oproti roku 2005 |
|
|
A | ||||
|
B | ||||
|
C | ||||
Zde musíme přemýšlet co nám jednotlivé údaje představují:
počet pracovníků q0 a q1
měsíční mzda p0 q0
změna mzdy ![]()
tato data známe, takže si pomocí nich vyjádříme ISS
![]()
![]()
V ofiko materiálech je to př. č. 3
Máme údaje o počtu pracovníků a vyrobené produkci ve dvou měsících v podniku, který má 3 provozovny :
|
Provozovna |
Počet pracovníků |
Celková produkce – počet vyrobených kusů (tis. ks) |
||
|
říjen |
prosinec |
říjen |
Prosinec |
|
|
A | ||||
|
B | ||||
|
C | ||||
Určete:
a) jak se změnila celková produktivita práce v podniku - IPS
b) jak byla změna celkové produktivity práce ovlivněna změnou počtu pracovníků v jednotlivých provozovnách - IST
c) jak byla změna celkové produktivity práce ovlivněna změnou produktivity práce v jednotlivých provozovnách - ISS
Zde celková produkce odpovídá … p*q (počet * produktivita)
… dál jsme si k tomu nic neříkali… takže by to asi mělo bejt jasný … já nevím, protože jsem to nepočítala
Pro procvičení př.6
V ofiko materiálech je to př. č. 2
|
Rok | ||||
|
Stav v předchozím roce = 1 |
Tady jsou 2 možnosti jak to počítat…
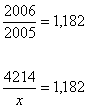 a tak se
postupně dopočítáme až k roku 2002
a tak se
postupně dopočítáme až k roku 2002
|
i=0 | ||||
|
|
|
|
|
Pak pomocí převedení řetězových indexů na bazické dostaneme výpočtový tvar….
![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]() … vykrátí se to
… vykrátí se to
![]()
Pozn. Pokud chci převést bazické indexy na řetězové tak se to nedělá přes součin ale přes podíl.
Indexy nestejnorodých ukazatelů
Nejdou shrnout přímo a proto se ohodnocují cenou
Cena … c
Množství … q
!!!Zde nelze
![]() nemůžu
sečíst litry s kilogramama atd.
nemůžu
sečíst litry s kilogramama atd.
![]() mělo by smysl jen kdybychom to brali jako vydání
peněz, ale tam by muselo být c*q
mělo by smysl jen kdybychom to brali jako vydání
peněz, ale tam by muselo být c*q
Hodnotový index
![]()
Indexy pro zjištění vlivu změny ceny
Passcheho
i. ![]()
Laspirisův
i. ![]()
Loweho
i. 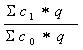
Fischerův
i. ![]() L..Laspir., PPassche
L..Laspir., PPassche
Indexy fyzického objemu IFO
Passcheho
i. ![]()
Laspirisův
i. ![]()
Loweho
i. 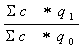
Fischerův
i. ![]() L..Laspir.,
PPassche
L..Laspir.,
PPassche
Příklady a jejich řešení
V ofiko materiálech je to př. č. 14
O vývoji cen a tržbách za tři mražené výrobky v prodejním stánku máme za první dvě čtvrtletí roku 2007 následující údaje:
|
Výrobek |
Hmotnost balení |
Ceny (Kč) |
Tržby (Kč) |
||
|
1. čtvrtletí |
2. čtvrtletí |
1. čtvrtletí |
2. čtvrtletí |
||
|
Zmrzlina borůvková |
250 gr | ||||
|
Zmrzlina jogurtová |
350 gr | ||||
|
Zmrzlina vanilková |
125 gr |
6 | |||
Vyjádřete :
a) změnu celkových tržeb,
b) jaký vliv na změnu celkových tržeb měla změna cen jednotlivých výrobků,
c) jaký vliv na změnu celkových tržeb měla změna prodaného množství jedotlivých výrobků,
d) jak se změnilo prodané množství jednotlivých výrobků,
e) pomocí Bortkiewiczova rozkladu vysvětlete příčinu rozdílu mezi Laspeyresovým a Paascheho cenovým indexem. - domácí úkol
Uděláme si tabulku:
… vypočteme si všechno co budeme potřebovat pro jednotlivé výpočty
|
c0 |
c1 |
c0 * q0 |
c1 * q1 |
q0 |
q1 |
ad A,
![]() = 1,09
= 1,09
ad B,
cenový index můžeme vypočítat jakým chcem vzorcem, my jsme počítali všema kromě Loweho
P = 1,03
L = 1,245
F = 1,132
ad C,
IFO
P = 0,875
L = 1,058
F = 0,952
ad D,
A Zmrzlina
borůvková… ![]() =
= ![]()
B Zmrzlina jogurtová … = 2,06
C Zmrzlina vanilková … = 0,42
K nárůstu prodaného množství došlo u B.
ad E,
Máme si udělat doma, návo by měl být na commonu a možná i výsledek. Prý to vypadá složitě, ale je to jednoduchý J já dodávám “jen aby” J
V ofiko materiálech je to př. č. 15
Na základě údajů o tržbách a změnách prodaného množství vyjádřete, jak se na změně celkových tržeb podílela změna cen jednotlivých výrobků.
|
Výrobek |
Tržby v roce 2006 (Kč) |
Změna prodaného množství v roce 2006 oproti roku 2005 |
|
A |
156200 | |
|
B |
1863500 | |
|
C |
9500 |
Zas si uděláme tabulku:
|
c1 * q1 |
q1 q0 |
c1 * q0 |
|
Suma 1830264 |
Máme zadaný nějaký indexy a kouknem se, jakej vzoreček by se nám nejlíp hodil, na kterej máme nejvíc proměnnejch vyšel z toho Passcheho
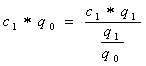 IFO P
=
IFO P
=![]() = 1,108
= 1,108
Došlo ke změně tržeb o 10,8%.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1673
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved