| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
|
T |
ento článek obsahuje jednoduchý popis a vysvětlení Einsteinovy speciální teorie relativity a její možné aplikování na FTL cestování (cestování rychleji než světlo). Předpokládá se, že čtenář nejprve pochopí základní rysy speciální teorie relativity tak, jak jsou zde popsány, především tedy s tzv. časoprostorovými diagramy. Tento článek by měl také ukázat, že FTL cestování je teoreticky možné bez porušení obou teorií relativity i jiných fyzikálních zákonů. V závěru článku budou všechny teorie přeneseny na teorie vznesené ve Star Treku.
Teorie relativity a FTL cestování
Obsah :
1. Představení speciální teorie relativity------------------------------------------- 2
1.1. Důvody existence teorie---------------------------------------------------------- 2
1.2. Dilatace času a kontrakce délek-------------------------------------------- 3
1.3. Konstanta c (gama) - Lorentzův koeficient------------------------------- 5
1.4. Energie a hybnost------------------------------------------------------------------- 5
1.5. Experimentální potvrzení teorie---------------------------------------------- 6
2. Časoprostorové diagramy------------------------------------------------------------------ 6
2.1. Co to jsou časoprostorové diagramy--------------------------------------- 6
2.2. Základní informace o TSD-------------------------------------------------------- 7
2.3. TSD pro jednoho nehybného pozorovatele-------------------------------- 7
2.4. Pohybující se pozorovatel------------------------------------------------------- 8
2.5. Záměna pojmů „v pohybu“ a „v klidu“---------------------------------------- 10
2.6. „Budoucnost“, „přítomnost“ a světelný kužel-------------------------- 10
3. Uvedení do diskuze o FTL cestování-------------------------------------------------- 12
3.1. Několik poznámek o významu FTL cestování---------------------------- 12
4. První problém : bariéra rychlosti světla-------------------------------------- 12
4.1. Efekty při přibližování se rychlosti světla------------------------------ 12
5. Druhý problém : FTL, příčinnost a neřešitelné paradoxy----------- 13
5.1. Co je myšleno příčinností a neřešitelným paradoxem--------------- 13
5.2. Jak může FTL cestování zahrnovat porušení příčinnosti----------- 14
5.3. Jak lze vytvořit neřešitelný paradox------------------------------------- 15
6. FTL koncepty a ohledem na výše uvedené problémy--------------------- 15
6.1. Tachyony (bez speciálních provizí)------------------------------------------ 16
6.2. Používání zvláštních polí, zvláštního prostoru apod. (bez speciálních provizí)------------------------------------------------------------------------------------------------- 17
6.3. „Ohýbání“ prostoru---------------------------------------------------------------- 17
6.4. Časoprostorové manipulace-------------------------------------------------- 17
6.5. Speciální provize------------------------------------------------------------------- 17
6.5.1. Paralelní vesmíry------------------------------------------------------------------------------------ 18
6.5.2. Důsledková ochrana-------------------------------------------------------------------------------- 18
6.5.3. Vytváření omezených zón časoprostoru-------------------------------------------------------- 18
6.5.4. Speciální vztažná soustava pro účely FTL cestování---------------------------------------- 20
7. Aplikování všeho výše na FTL cestování ve Star Treku---------------- 21
7.1. Která provize se nejlépe hodí k vysvětlení Hyperprostorového (Warp) cestování------------------------------------------------------------------------------------------------- 21
7.2. Hyperprostor jako speciální vztažná soustava----------------------- 22
7.3. Shrnutí hyperprostrorového cestování---------------------------------- 22
7.4. Poznámky k jiným druhům FTL cestování a cestování v čase ve Star Treku 22
8. Na závěr…----------------------------------------------------------------------------------------------- 23
9. Literatura--------------------------------------------------------------------------------------------- 23
Základní účel tohoto představení bude přiblížit teorii především těm, kteří se s ní předtím podrobně nezabývali nebo se s ní setkávají poprvé. Také může sloužit jako jakýsi souhrn pro ty, kterým je již známa. Nebudeme postupovat běžnou cestou výkladu teorie, která je založená na „sledování“ jejího vytváření, ale začneme před-Einsteinovými vizemi relativity. To nám pomůže bez složité matematiky dokázat, že je Einsteinův pohled správný. To dále povede k diskuzi nad důsledky, jaké by bylo možno pozorovat, a nakonec uvedu některé známé experimentální důkazy teorie.
Nápad relativnosti přišel na svět již v Newtonových časech, ale nepodařilo se ho dokončit. Umožňovala vysvětlit, jak vypadá pozorovaní jednoho pozorovatele, který se pohybuje vzhledem k druhému pozorovateli. Tomu se říká přechod z jedné vztažné soustavy k druhé. Tato transformace nebyla před Einsteinem chápána správně, ale přesto platila u nízkých (pozemských) relativistických rychlostí.
Než budeme pokračovat, rád bych se pozastavil u významu spojení „vyskytnout se ve vztažné soustavě“. Vztažná soustava znamená něco jako úhel pohledu jednotlivého pozorovatele. Nicméně, toto vysvětlení by mohlo některé nováčky, kteří se s ní dosud nesetkali, uvést v omyl. Proto uvedu názornější popis. Pokud hovoříme o tom, že se něco stane v některé vztažné soustavě, netvrdíme, že to pozorovatel v této soustavě opravdu uvidí. To proto, že pozorovatel (například) může vidět událost teď, ale pokud se ve skutečnosti odehrála na deset světelných let vzdálené hvězdě v pozorovatelově vztažné soustavě, musí říci, že se odehrála v jeho soustavě před deseti lety. Uvádím to proto, že nováčci se často domnívají, že se jedná jen o vedlejší efekty (podobně jako např. dilatace času - viz dále) způsobené tím, že světlo pocházející z události může dorazit k jednomu pozorovateli dříve než k druhému. Tímto tedy dodávám : pokud budeme hovořit o výskytu události ve vztažné soustavě, vždy máme na mysli dobu skutečného výskytu události v soustavě po odpočítání všech zpoždění světelných signálů.
Podobně, pokud řeknu, že události A a B se odehrály simultánně v některé vztažné soustavě, nemyslím též, že je pozorovatel v této soustavě uvidí stát se zároveň, ale že se ve skutečnosti zároveň odehrály. Například : dvě exploze se odehrají opravdu simultánně, ale jedna na Měsíci a druhá u Slunce, potom uvidíme první tu, která se vyskytla na Měsíci (protože je to blíž). Musíme tedy vzít v úvahu dobu, po jakou k nám světlo informaci o události dopravuje. Posléze tedy vyvodíme, že obě exploze se odehrály opravdu současně v naší vztažné soustavě. Je si tedy důležité zapamatovat, že takto uvažujeme o tom, kdy a kde se události odehrávají v různých vztažných soustavách.
Nyní si uvedeme příklad Newtonského náhledu na přechod z jedné soustavy do druhé. Představte si dva pozorovatele, např. mne a vás. Řekněme, že já jsem ve vlaku jedoucím rychlostí 30 km/h. Hodím míček ve směru jízdy vlaku tak, že vzhledem ke mě se pohybuje rychlostí 10 km/h (hodím ho tedy touto rychlostí). Na vlaku si představte nakreslený svislý barevný pruh. Pokud míček držím (ještě jsem ho nehodil), pohybuje se stejnou rychlostí jako já a celý vlak. Když ho hodím, uvidíte, že se míček přibližuje oné svislé čáře. Podle vás se tedy míček pohybuje rychleji než já (a vlak). Rychlost míčku vzhledem k vám je součet jeho rychlosti vzhledem ke mě a má rychlost (rychlost vlaku) vzhledem k vám. V našem vzorci představuje proměnná v rychlost míčku vzhledem k vám.
![]()
Takto vznikl první postup převodu rychlosti z jedné vztažné soustavy do druhé. Snaží se popsat relativní vztahy mezi pozorováním jednoho pozorovatele vzhledem k pozorováním druhého. Je to tedy základní koncept teorie relativity, je ovšem velmi neúplný.
Teď přichází čas na představení důležitého postulátu, který vede ke konceptům relativity. Cituji z Serwayovy fyzikální knihy : „ zákony fyziky jsou stejné ve všech inerciálních vztažných soustavách“ (inerciální vztažnou soustavou se v zásadě myslí ta, která se pohybuje rovnoměrně a přímočaře). Tento postulát znamená, že pokud se dva pozorovatelé pohybují různou, ale konstantní rychlostí, a jeden z nich pozoruje fyzikální zákony na jisté události, potom druhý z nich musí také souhlasit, že ony fyzikální zákony platí a pracují stejně.
Jako příklad použijeme hybnost (kterou stručně vysvětlím dále). Řekněme, že dva míče se přímo proti sobě přibližují. Střetnou se a každý odletí v obráceném směru. Tento příklad říká, že pokud sečteme celkovou hybnost obou míčů (která se u malých rychlostí rovná násobku hmotnosti a rychlosti míče) před srážkou a obou míčů po ní, obě hodnoty budou stejné. Dejme tomu, že se onen experiment odehrává v jedoucím vlaku a jeden míč se pohybuje ve směru a druhý v protisměru jízdy vlaku. Vnitřní pozorovatel by řekl, že začáteční i koncová rychlost míčů je identická, zatímco pozorovatel vně vlaku by řekl, že se mírně liší. Nicméně, oba pozorovatelé se musí shodnout, že celková hybnost byla zachována (součet byl konstantní). Jeden z nich by řekl, že celková hybnost zůstala zachována, protože (A) hybnost před a po kolizi byly stejné, zatímco druhý, protože (B) hybnost před a po byly odlišné. Neschodnou se tedy na konkrétních sčítancích, ale na tom, že jejich součet byl stejný a zákon tedy platí. Tento postulát lze uplatnit na jakýkoliv fyzikální zákon. Pokud ne (fyzikální zákony by se lišily v různých vztažných soustavách), potom bychom mohli změnit zákony fyziky pouze cestováním do konkrétní soustavy.
Velmi zajímavých výsledků dosáhneme, pokud tento postulát uplatníme na zákony elektrodynamiky. Pokud uvážíme, že tyto zákony musí být stejné v každé inerciální vztažné soustavě, potom musí také rychlost elektromagnetických vln (jako např. světlo) být stejná pro všechny inerciální pozorovatele. Toto konstatování není zase tak zarážející, má ale „omračující“ následky. V našem příkladu (kdy jsem já házel z vlaku míč a vy jste stál mimo vlak) nahradíme míček světelným svazkem. Pokud se vlak pohybuje polovinou rychlosti světla (c/2) a světelný paprsek přesně rychlostí světla vzhledem ke mě, nepředpokládal byste, že světelný svazek se bude vzhledem k vám pohybovat 1,5 násobkem rychlosti světla ? Podle výše uvedeného postulátu se tak ale nestane a všechny způsoby vysvětlit tuto neshodu pomocí Newtonovy fyziky ztroskotají. Všichni pozorovatelé se shodnou, že rychlost jakéhokoliv světelného svazku je přesně c, bez ohledu na vztažnou soustavu. Přestože tedy zjistím rychlost svazku, který jsem vyslal z vlaku, tj. c vzhledem ke mě a vy mě uvidíte cestovat kolem vás polovinou rychlosti světla, musíte také přiznat, že rychlost svazku je c i vzhledem k vám.
V této kapitole popíšu způsob, jak může dilatace času pomoci vysvětlit zvláštnosti, které vyplývají z výše uvedeného postulátu. Opět budeme uvažovat případ, kdy já jsem ve vlaku a vy mimo něj, ale vlak se tentokrát bude pohybovat rychlostí 0,6c vzhledem k vám. Já (ve vlaku) vyzářím světelný impuls přímo nahoru (kolmě k podlaze vlaku), na stropě se impuls odrazí opačným směrem (pomocí zrcadla rovnoběžného s podlahou) a opět u podlahy ho nějakým senzorem zachytím. Z vašeho pohledu mimo vlak ale impuls neopíše dvakrát úsečku, ale jeho trajektorie bude vypadat jako obrácené „V“, což způsobí pohyb vlaku. Tuto situaci, viděnou z vaší vztažné soustavy, vidíte na diagramu 1.1
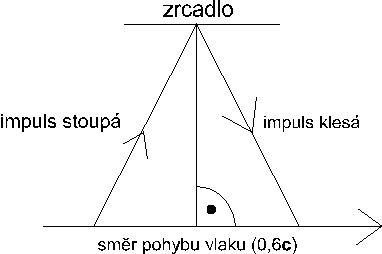
Obrázek 1-1
Řekněme, že cesta impulsu vzhůru bude trvat 10 sekund z vašeho pohledu. Vzdálenost, jakou vlak ujede za tuto dobu je dána součinem tohoto času a jeho rychlosti :
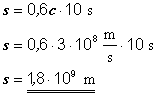
Vzdálenost, kterou světlo urazí od podlahy ke stropu je dána opět součinem rychlosti (která musí být i vzhledem k vám c, jak bylo uvedeno výše) a času (opět 10 sekund).
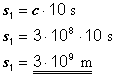
Protože levá strana našeho obráceného „V“ je pravoúhlý trojúhelník, ve kterém známe délku přepony (cesta světelného impulsu) a jednu odvěsnu (dráha, kterou vlak ujel), můžeme vypočítat výšku vlaku pro náš experiment pomocí Pythagorovy věty (h znamená výška vlaku) :
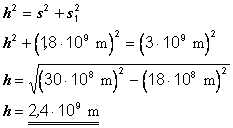
(Bude to skutečně vysoký vlak, když uvážíme, že světlu trvá 10 sekund, než dorazí od podlahy ke stropu, ale je to jen myšlený experiment). Nyní se zaměříme na mou vztažnou soustavu ve vlaku. Světlo opět bude mít rychlost c a výška vlaku se nemění, protože relativita nemá vliv na délky kolmé ke směru pohybu. Proto můžeme vypočítat, jak dlouho bude světlu trvat, než dorazí ke stropu v mé vztažné soustavě. To je dáno podílem vzdálenosti (výšky vlaku) a rychlosti (c) :
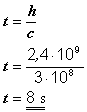
a tady to máme ! Pro vás celá událost trvá 10 sekund, zatímco podle mého pozorování pouze 8 sekund. Jak vidíte, pro vás je vzdálenost, kterou světlo uletělo, delší než je výška vlaku (viz diagram 1.1). Takže jediný způsob, jak já (ve vlaku) mohu říci, že světlo uletělo výšku vlaku, zatímco vy říkáte, že stejný světelný impuls uletěl delší vzdálenost, je, že buď (1) máme do činění s různými rychlostmi světla nebo (2) různou představou o trvání letu světla, protože jsme v jiných vztažných soustavách. V Newtonových dobách by si mysleli, že prvně uvedené je pravdivé. Na světlo by se pohlíželo stejně jako např. na míč a pozorovatelé v různých soustavách by jen viděli různé relativní rychlosti světla (viz náš první vlakový příklad). Nicméně, pomocí principů Einsteinovy relativity víme, že rychlost světla je narozdíl od jiných rychlostí nezávislá na vztažné soustavě. Pravdivé je tedy druhé vysvětlení a z vašeho pohledu jdou mé hodinky (v rychle se pohybujícím vlaku) pomaleji než vaše.
Jak jsem poznamenal v poslední části minulé kapitoly, kontrakce délek je další důsledek relativity. Představme si opět náš vlakový příklad. Tentokráte budeme držet oba horizontálně metr dlouhou tyč (tyč bude tedy orientována ve směru jízdy vlaku). Pro venkovního pozorovatele (vás) bude tyč cestovatele (má) kratší než jeden metr. Někteří sice mohou odvodit spojitost s dilatací času, ale nebudeme za příčinu tohoto efektu považovat čas.
Důležité upozornění ! Někdo by si také mohl myslet něco ve smyslu „pokud se pohybujete, zpomaluje se pro vás čas“. Ovšem otázka, pro koho se skutečně zpomaluje čas (pro mě nebo pro vás) nemá jednoznačnou odpověď ! Je nutné si uvědomit, že všechny rychlosti jsou relativní, tedy že neexistuje absolutní pohyb nebo klid. Nelze tedy říci, že to je vlak, který se absolutně pohybuje a vy jste v absolutním klidu. Určitě jste někdy zažili, že sedíte ve stojícím autě a náhle máte pocit, že couváte. Brzy si však uvědomíte, že to vlastně je auto ve vedlejším pruhu, které se „ve skutečnosti“ pohybuje dopředu. Ovšem jediným důkazem, proč je tomu skutečně tak, je to, že vidíte své okolí „v klidu“ a že se jedná o ono druhé auto, které se vzhledem k tomuto okolí pohybuje. Dokud byste se tedy nepodíval na okolní krajinu, neměl byste jedinou možnost zjistit, kdo se „ve skutečnosti“ pohybuje. Pokud by se podobná událost odehrávala ve vesmíru, kde by nebyl žádný referenční bod, o kterém víte, že se nepohybuje, nebyl byste vůbec schopen zjistit, která z vesmírných lodí (vaše nebo míjející) se opravdu pohybuje. Dokud je tedy vztažná soustava v klidu nebo v rovnoměrném přímočarém pohybu (jedná se tedy inerciální soustavu), neexistuje na tuto otázku žádná absolutní odpověď. Druhá loď se pohybuje vzhledem k vám a vy vzhledem k ní. Všechny pohyby jsou relativní a všechny inerciální vztažné soustavy jsou si rovnocenné.
Co to pro nás znamená v našem vlakovém příkladu ? Ve skutečnosti si já mohu myslet, že jsem v klidu a vy mě míjíte rychlostí 0,6c. Protože tedy mohu uplatnit koncepty relativity stejně dobře jako vy (to je základní postulát teorie relativity - všechny fyzikální zákony jsou totožné pro všechny inerciální pozorovatele) a z mého pohledu jste to vy, kdo je v pohybu, mohu si myslet, že váš čas se zpomaluje a vaše metrová tyč se zkracuje.
Opět tedy neexistuje absolutní odpověď na to, kde dochází k dilataci času a kontrakci délek. Jediná logická odpověď je, vždy se odkázat na vztažnou soustavu, o které uvažujeme. V mé soustavě váš čas plyne pomaleji než můj, ale ve vaší soustavě můj čas plyne pomaleji než váš. To vede k takzvanému paradoxu dvojčat (který se dá lapidárně přirovnat k tomu, že si každý myslí,. že hodinky druhého jdou pomaleji než jeho vlastní). Pochopení těchto paradoxů je klíčem k pochopení všech základních konceptů teorie relativity.
Čím více se přibližujeme k rychlosti světla, tím pomaleji ubíhá náš čas a zkracují se předměty ve směru pohybu ve vztažné soustavě pozorovatele. Faktor dilatace času a kontrakce délek je c (gama) a nazývá se Lorentzův koeficient.
c pro objekt pohybující se rychlostí v vzhledem k vaší vztažné soustavě je definována jako :

Pro náš vlak (který se ve vztažné soustavě pohybuje rychlostí v = 0,6c) činí c 1,25. Délky budou zkráceny a čas zpomalen (viděno očima venkovního pozorovatele - vás) o faktor 1/c = 0,8. To je přesně tolik, kolik jsme vypočítali při našem pokusu se světelným impulsem, který letěl od podlahy ke stropu 10 sekund podle vás (viděno mimo vlak) a 8 sekund podle mě (ve vlaku). c je skutečně velmi důležitou proměnnou při práci s teorií relativity, včetně efektů speciální teorie relativity, především počty s energií a hybnosti.
Dalším důsledkem relativity je spojitost mezi hmotností, energií a hybností. Připomínám, že rychlost nám odpovídá na otázku, jak daleko a jak dlouho se pohybujeme. Samozřejmě, pokud relativita mění způsob, jak pozorovatelé vnímají délky a čas relativně k jiným, mohlo by připadat, že veškeré Newtonovské koncepty týkající se pohybu musí být přepracovány. Například, díky relativitě nelze jednoduše sčítat rychlosti při změně vztažné soustavy jako v našem příkladu s míčem. Je ovšem třeba připomenout, že u malých (pozemských) rychlostech jsou tyto chyby zanedbatelné.
Dále, hybnost (která je v Newtonovské mechanice definován jako součin hmotnosti a rychlosti) není zachována v různých vztažných soustavách při jejich interakci. Tento vztah je definován vzorcem :
![]()
Kde c je proměnná definovaná výše.
Po dalším uvažování hybnosti a energie viděno z dvou vztažných soustav zjistíme, že následující rovnice musí platit pro celkovou energii nevázané částice :
![]()
kde E je energie, m hmotnost a p relativní hybnost definována výše.
Po dalších ekvivalentních úpravách dostaneme jiný výraz pro definici celkové energie :
![]()
Zde je třeba opět připomenout, že pokud je objekt v klidu (c = 1), vyjde nám všeobecně známý vzorec
![]()
který říká, že hmota samotná „obsahuje“ energii.
Nyní je třeba upřesnit, že hmotnost ve vzorcích a rovnicích výše má speciální definici, kterou nyní probereme. Když se cestovatel přibližuje rychlosti světla vzhledem k (nepohybujícímu se) pozorovateli, pozorovateli se zdá, že „hmotnost“ cestovatele roste. (Jako „hmotnost“ máme na mysli často buď (1) kolik síly potřebujeme k jistému zrychlení nebo (2) jaký gravitační tlak ucítíte v Newtonské gravitaci - tedy tíhu). Nicméně, ve všech výše uvedených případech měříme hmotnost v nehybné soustavě tohoto objektu. Tato hmotnost je vždy stejná. Často se „viditelná hmotnost“ viděná vzdálenému pozorovateli (nazývám ji „pozorovaná hmotnost“ - mp) definována jako mc. Protože jsme výše definovali energii jako
![]()
můžeme též zapsat celkovou energii jako :
![]()
Tato pozorovaná hmotnost dosahuje nekonečna, když se objekt přibližuje rychlosti světla vzhledem k pozorovateli (protože c se také přibližuje k nekonečnu).
Dále je třeba připomenout případ, kdy klidová hmotnost objektu je nulová (jako např. u fotonu). Ze vzorce pro energii lze odvodit, že pokud m = 0, potom je nulová i energie částice. Nicméně, tato částice je schopna jako málokterá pohybovat se rychlostí světla. Vzorec pro výpočet energie má tedy dvě části : c je nekonečno a m je nula. Není tedy nemožné, že při této rychlosti se nějaká energie může vyskytnout. Toto tvrzení je ještě podtrženo vzorcem
![]()
kde po vykrácení (m = 0) nám zbyde
![]()
Protože foton má hybnost (může např. „udeřit“ do částic a změnit jejich pohyb), která je definována jeho vlnovou délkou, lze říci, že energie podle pc může být i pokud částice nemá žádnou klidovou hmotnost.
Tyto obdivuhodné důsledky relativity mají experimentální potvrzení. Jeden z jich je známý příklad s částicemi zvanými mezony, které jsou obsaženy v kosmickém záření ze Slunce v horních vrstvách atmosféry. V nehybné vztažné soustavě existují mezony jen asi 2,2×10-6 sekund. Přestože mezony dovedou dosáhnout rychlosti světla, mohou stále uletět za dobu své existence jen asi 660 metrů. Díky tomu by pochopitelně nemohly dosáhnout pozemské atmosféry. Bylo ovšem pozorováno, že jejich velké množství Zemi dosáhne. Z našeho pohledu se čas ve vztažné soustavě jednoho mezonu zpomaluje, protože se vzhledem k nám pohybuje velmi rychle. Takže oněch 2,2×10-6 sekund se zpomalí a mezony mají dostatek času dorazit k Zemi.
Jsme ovšem schopni celou záležitost vysvětlit i z mezonovy vztažné soustavy. Z pohledu této částice trvá její existence jen 2,2×10-6 sekund, nicméně se z tohoto pohledu také zdá, že se Země velmi rychle přibližuje a vzdálenost od Slunce k pozemské atmosféře se zkrátí. Z pohledu mezonu sice žije jen velmi krátkou dobu, ale stačí mu uletět jen velmi krátkou vzdálenost. Toto dokazuje další zajímavý bod relativity - fyzikální zákony musí dát pro všechny pozorovatele stejný výsledek (tj. mezon dorazí do pozemské atmosféry), jejich vysvětlení se však může lišit od jedné vztažné soustavy k druhé.
Ve všech výše uvedených odstavcích jsme vlastně stále hovořili jen o dilataci času a kontrakci délek. Teorie relativity je však pro lepší pochopení doplněna teoriemi a postupy, které popíši v dalších odstavcích.
V této části si povíme něco o konstrukcích takzvaných časoprostorových diagramů. Po krátkém vysvětlení jejich účelu vysvětlím, jak je ve skutečnosti správně chápat. Stejným způsobem se potom pokusíme sestavit diagram pro pozorovatele vzhledem k jiné vztažné soustavě. Takovýto diagram nám ukáže vztažnou soustavu druhého pozorovatele vzhledem k prvnímu a naopak. Nakonec porovnáme význam výrazů minulost a budoucnost pro různé pozorovatele a shrneme je do pojmu světelný kužel.
V minulé části jsme hovořili o hlavních důsledcích Speciální teorie relativity a nyní se zaměříme na to, jak relativita zasahuje do transformace prostoru a času. Jedním z důsledků je např. to, že dva různí pozorovatelé mohou mít různé časoprostorové souřadné soustavy. Souřadnice lze převést z jedné soustavy souřadné do jiné pomocí Lorentzovy transformace. Tyto transformace lze pochopit díky časoprostorovým diagramům bez složitých matematických vzorců
Na časoprostorovém diagramu (dále jen TSD) lze najednou zobrazit různé události odehrávající se na různých místech a v různých časech. Každá událost je zaznačena jako bod v souřadné soustavě TSD. Díky relativitě budou mít ve skutečnosti různí pozorovatelé pro tytéž události různé souřadnice. Na TSD lze vyobrazit tyto různé souřadné soustavy na jednom diagramu, což nám pomůže lépe pochopit jejich souvislost. Pro jednoduchost se v našich TSD omezíme na dvourozměrný časoprostor (jeden rozměr prostoru a druhý rozměr čas).
V našich diagramech budeme pro jednoduchost užívat jen jeden rozměr prostoru a to na ose x. TSD se tedy skládají z jedné osy označující prostor a druhé (k první kolmé) označující čas (značené t). Obě osy se protnou v jednom bodě, který je definován jako x = 0; t = 0. Na diagramu 2-1 je nakreslen takový prázdný TSD.

Diagram 2-1

Diagram 2-2
Dále je třeba definovat jednotky, které budou určovat polohu a čas na diagramu. Nejvhodnější jednotkou pro čas je asi sekunda. To znamená, že pokud se posuneme vzhůru po ose t o jednu jednotku, znamená to totéž jako čekat jednu sekundu. Pro polohu (prostor) definujme jednotku světelnou sekundu (vzdálenost, kterou uletí světlo ve vakuu za sekundu). Pokud se tedy posuneme o jednu jednotku doprava na ose x, budeme se na svou bývalou pozici dívat ze vzdálenosti jedné světelné sekundy.
Pro představu nakreslíme do diagramu 2-2 světelný paprsek pohybující se ve vakuu. Paprsek vyjde z počátku soustavy souřadné a bude vyslán doprava. Protože světelný paprsek uletí za jednu sekundu vzdálenost jedné světelně sekundy, hodnoty souřadnic x a t se budou u polopřímky, která tento paprsek naznačuje, shodovat. Tato polopřímka bude tedy svírat s oběma osami úhel 45°.
V tomto bodě se přesně rozhodneme, jak budou zaznamenány dané události pro jednotlivého pozorovatele. Nejprve je třeba připomenout, že každý TSD je speciálně „navržen“ pro jednoho pozorovatele. Na diagramu 2-1 je tento pozorovatel ten (nazývejme ho pozorovatel O), kterému přísluší navzájem kolmé osy na diagramu zaznačené. Jiná vztažná soustava (která není představována těmito osami) může být zaznačena na tomže diagramu. Nicméně, protože jsme za souřadný systém vybrali dvě kolmé osy, je přirozené si myslet, že tento TSD byl nakreslen vzhledem k pozorovateli O. Lze tedy říci, že v tomto TSD je pozorovatel O „v klidu“.
Pokud je pozorovatel O nejprve v počátku, potom jednu sekundu později je stále na souřadnici x = 0 (protože se nepohybuje), o dvě sekundy také, atd. To v zásadě znamená, že všechny přímky rovnoběžné s časovou osou představují stálou pozici.
Dále je třeba určit způsob, jak zakreslit přímky s konstantním časem. Nejprve musíme najít bod na diagramu, který představuje událost, která se stala ve stejném čase jako počátek (t = 0). Použijeme stejný způsob, jako poprvé Einstein. Na ose t najdeme událost, která se stala před t = 0, jako např. v čase t = -3. V tomto čase vyšleme paprsek světla v kladném směru (doprava). Pokud se paprsek odrazí od vzdáleného zrcadla v čase t = 0 a poletí zpět k ose t, potom k nám dorazí v t = 3 sekundy. Z toho usoudíme, že se světlo odrazilo v čase t = 0, simultánně s počátkem.
Abychom toto zakreslili na diagram, zavedeme si dva body (např. A a B), které ukazují na t = -3, respektive t = 3 (viz diagram 2-3). Potom zaznačíme paprsek opouštějící bod A v kladném směru a paprsek, který přichází do bodu B v záporném směru. Průsečík těchto polopřímek označme C. Tento bod znamená událost simultánní s počátkem. Přímka procházející počátkem a C (a všechny přímky s ní rovnoběžné) je tedy přímkou konstantního času. Všechny události, které leží na téže přímce v této vztažné soustavě se odehrály současně. Na diagramu 2-4 vidíme několik navzájem rovnoběžných přímek jak pro prostor, tak pro čas.
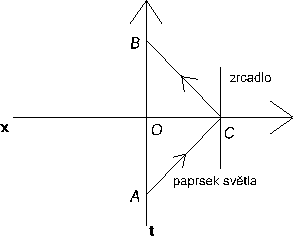
Diagram 2-3
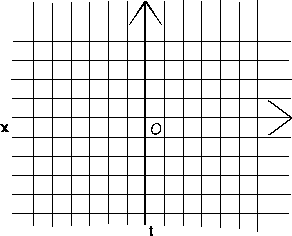
Diagram 2-4
Náš TSD také funguje, pokud na něj potřebujeme zakreslit pozorovatele, který se vzhledem k nehybnému O pohybuje. Nyní ale potřebujeme nakreslit TSD pro tohoto pohybujícího se pozorovatele. Trajektorie dvou pohybujících se pozorovatelů jsou nakresleny na diagramech 2-5 a 2-6. Podotýkám, že budeme většinou hovořit o pozorovateli, který míjí pozorovatele O v počátku (x = 0, t = 0). Počátek bude tedy představovat událost „pohybující se pozorovatel a pozorovatel O (který je v klidu) se míjejí“.
Cestovatel na diagramu 2-5 se pohybuje pomaleji než ten na diagramu 2-6, což poznáme podle úhlu sklonu trajektorie a osy t (přímá úměrnost) nebo osy x (nepřímá úměrnost).

Diagram 2-5

Diagram 2-6
Co tato polopřímka vlastně znamená ? Připomeňme, že ukazuje pozici našeho pozorovatele v různém čase. Představme si ale jiného pozorovatele, který sedí těsně vedle cestovatele (v podstatě na téže polopřímce), potom z jeho pohledu se cestovatel nepohnul. Polopřímka tedy ukazuje konstantní pozici pro pohybujícího se pozorovatele, nic se na jí vzhledem k němu nepohybuje. To znamená, že polopřímka představuje pro pohybujícího se pozorovatele totéž co osa t pro O a stává se tak pro něj novou osou t (označíme ji t´). Všechny přímky rovnoběžné s touto osou budou také představovat konstantní pozici pro pohybujícího se pozorovatele.
Stejně jako jsme to udělali pro pozorovatele O, vytvoříme osu konstantního času pro pozorovatele v pohybu. Pro zjištění osy použijeme stejnou metodu jako předtím. Pohybující se pozorovatel vyšle světelný paprsek v čase t´ = -T a ten se odrazí od zrcadla tak, že se vrátí k pozorovateli v čase t´= T. Protože světlo se pohybuje stejně rychle ve všech směrech pro všechny pozorovatele, pozorovatel musí konstatovat, že paprsku trvala cesta k zrcadlu a zpět stejnou dobu v jeho vztažné soustavě. Protože v jeho soustavě vyslal světlo v t´ = -T a vrátilo se v t´= T, potom se od zrcadla odrazilo simultánně z počátkem soustavy souřadné, tedy t´= t = 0 ve vztažné soustavě pohybujícího se pozorovatele.
Zde se naskýtá vhodný čas pro připomínku. Co by se stalo, kdybychom nevyslali světelný paprsek, ale míč s rychlostí 0,5c, který by se odrazil od stěny a vrátil se stejnou rychlostí. Pokud bychom chtěli takto najít přímku konstantního času pro pohybujícího se pozorovatele, míč by musel cestovat rychlostí 0,5c oběma směry ve vztažné soustavě pohybujícího se pozorovatele. Protože jsme ještě nedefinovali souřadný systém pro pohybujícího se pozorovatele, nevěděli bychom, jak by míč, který se pohybuje rychlostí 0,5c, vypadal na diagramu vzhledem k pozorovateli. Nicméně, základní postulát Teorie relativity říká, že rychlost světla se nemůže měnit od jednoho pozorovatele k jinému, proto světelný paprsek, který se pohybuje rychlostí c vzhledem k pohybujícímu se pozorovateli, se také pohybuje toutéž rychlostí vzhledem k O. Přímka se sklonem 45° k ose t nebo x představuje vždy paprsek světla, pohybující se rychlostí c pro všechny pozorovatele ve všech vztažných soustavách.
Na diagramu 2-7 je zaznačena událost A´ na ose t´, která se stane jistý čas před t´ = 0, a událost B´, která se stane totéž množství času, ale po t´ = 0. Jako předtím, je zde lomená čára, jedna část vyslaná z A´ doprava a druhá se vrací doleva do bodu B´. Na zlomu lomených čar (průsečíku polopřímek) je bod C´, který zaznačuje událost odrazu světla od zrcadla. Události C´ a O se odehrají simultánně ve vztažné soustavě pohybujícího se pozorovatele. Připomínám, že pro pozorovatele O je událost C´ nad jeho přímkou simultánosti (osa x). Pohybující se pozorovatel O´ tedy usoudí, že událost C´ se odehrála, když se oba pozorovatelé minuli v počátku s.s., zatímco pozorovatel O řekne, že událost C´ se odehrála po tom, co se oba pozorovatelé minuli. Probereme toto pojetí minulosti a budoucnosti dále v kapitole 2.6. Na diagramu 2-8 je zaznačena přímka probíhající body O a C´, která představuje pro pohybujícího se pozorovatele totéž, co osa x pro pozorovatele O. Je tedy označena x´.
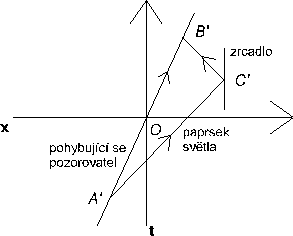
Diagram 2-7

Diagram 2-8
Z geometrického znázornění prostorové osy lze odvodit všeobecné pravidlo na hledání x-ové osy pro pohybujícího se pozorovatele. Nejprve si připomeneme, že osa t´ je přímkou, která představuje pozici pohybujícího se pozorovatele na TSD. Čím rychleji se pozorovatel O´ pohybuje vzhledem k O, tím je větší úhel mezi osou t a t´. Osa t´ je tedy zrotovaná osa t o jistý úhel po nebo proti směru hodinových ručiček (podle toho, zda se pozorovatel pohybuje doprava nebo doleva). Osa x´ je potom přímka rotovaná o stejný úhel od osy x, ale v opačném smyslu (360-a).
Jak si již jistě sami odvodíte, osa x´ je přímka konstantního času pro O´, stejnětak jako každá jiná rovnoběžná přímka. Tyto přímky s přímkami konstantní pozice vytvoří mříž a novou soustavu souřadnic pro pozorovatele O´. Takováto mříž je znázorněna na diagramu 2-9. Pokud si vybereme na tomto TSD jeden bod, oba pozorovatelé se neshodnou, kdy a kde se daná událost odehrála (protože je zaznamenána ve dvou souřadných systémech).
Diagram 2-9
Na závěr kapitoly bych připomněl, že oba s.s. vypadají tak jak vypadají, jen díky tomu, že rychlost světla je absolutně konstantní.
Pro plné porozumění časoprostorových diagramů musíme do nich dále zavést postulát o inerciálních vztažných soustavách, tedy o tom, že všechny vztažné soustavy, které se pohybují rovnoměrně a přímočaře, jsou si rovnocenné, a o tom, že veškerý pohyb je relativní. Původně jsme předpokládali, že O je pozorovatel v klidu, jen proto, protože byl tak definován. Definice pozorovatele O´ říkala, že se pohybuje vzhledem k O.
Nicméně, naprosto jednoduše lze také definovat pozorovatele O´ stacionárním a pozorovatele O, který se od něj vzdaluje doleva. Potom budeme moci označit x´ a t´ horizontální a vertikální osu, zatímco zrotované osy se stanou x a t. Takovýto TSD je na diagramu 2-10. Po jeho zhlédnutí zjistíte, že se opravdu jedná jen o diagram 2-8, který byl rotován tak dlouho, dokud původně zrotované osy x´a t´ se stanou horizontální a vertikální.

Diagram 2-10
Pro to, abychom se mohli dále zabývat FTL cestováním, musíme si vysvětlit význam slov „budoucnost“ a „minulost“ na časoprostorových diagramech. Tyto významy sice mají teoreticky stejný význam jako v běžném životě, mění se ovšem velmi rezolutně od jednoho pozorovatele k druhému. Nejprve musím opět připomenout, že nelze naprosto úplně srovnávat s.s. různých pozorovatelů, což je zapříčiněno tím, že neumíme porovnat jednotky délky a času ve vztažné soustavě pozorovatele O s délkami a časem, které stejné jednotky představují pro pozorovatele O´. Tímto problémem se zabývá podrobně Obecná teorie relativity. Nicméně, můžeme stále porovnávat význam výrazů minulost a budoucnost.
Vraťme se opět k diagramu 2-8. Jak jste si možná již všimli, je na něm kromě pozorovatelů O a O´ ještě hvězdička, která zaznačuje jistou událost. Jak už bylo řečeno, všechny události na ose x se udály ve stejný okamžik jako počátek (tj. událost, kdy se oba pozorovatelé míjejí). Protože námi vyznačená událost je pod touto osou, pozorovatel O se domnívá, že se udála před tím, než se pozorovatelé minuli. Také pro pozorovatele O´ znamená osa x´ události, které se staly simultánně s událostí míjejí se. Protože se zaznačená událost nachází nad osou x´, pozorovatel O´ se domnívá, že se událost odehraje až poté, co se mine s O. Závěrem lze říci, že kde a kdy se události odehrávají vzhledem k jiným závisí na konkrétní vztažné soustavě. TSD potom neukazují, kde a kdy byla událost viděna nebo zaznamenána, ale kdy a kde se opravdu odehrála. Jak je ovšem možné, že jedna událost může být minulostí jednoho pozorovatele a zároveň budoucností druhého ? Pro vysvětlení, proč se taková situace vlastně sama nepopírá, se podíváme na další známou konstrukci TSD.
Na diagramu 2-11 jsou nakresleny dva světelné paprsky, jeden cestující směrem x (doprava) a druhý směrem -x (doleva). Někde v negativním čase byly paprsky namířeny na x = 0 (do počátku). Tohoto bodu v prostoru dosáhnou v čase t = 0 a zkříží se. Se vzrůstajícím časem se opět vzdalují od x = 0. Tato konstrukce je známa jako světelný kužel.

Diagram 2-11
Světelný kužel dělí TSD na dvě hlavní části : na plochu uvnitř kuželu a na plochu vně. (Pro úplnost připomínám, že kužel, který je na diagramu 2-11 a o kterém hovoříme, se nazývá „světelný kužel se středem v počátku s.s.“). Pozorovatel v počátku, např. nám známý O, přijímá nebo vysílá signál v čase t = 0. Pokud tento signál sám vyšle, potom událost příjmu signálu někým jiným bude nad osou x, tedy v budoucnosti pro O. Pokud tento signál přijme, potom událost vyslání signálu bude v jeho minulosti, tedy pod osou x. Protože je nemožné, aby kdokoliv se pohyboval rychleji než světlo, potom jediné události, které bude moci pozorovatel O (v čase t = 0) zaznamenat, budou ležet uvnitř světelného kuželu (a pochopitelně pod osou x). Podobně, veškeré události, které může pozorovatel O ovlivnit do budoucna, opět leží uvnitř kuželu.
Nejpodstatnější věcí ve vztahu ke světelném kuželu je to, že jeho pozice je stejná pro všechny pozorovatele (protože rychlost světla je stejná pro všechny pozorovatele). Jako příklad si vezmeme „šikmý“ souřadný systém pohybujícího se pozorovatele O´ a naznačíme na něm výše uvedený světelný kužel. Pokud se posuneme jednu jednotku „dolů“ po ose x´ (posuneme se o vzdálenost jedné světelné sekundy) a „nahoru“ po ose t´ (uběhne jedna sekunda), potom bod, na kterém se nacházíme, bude ležet někde uvnitř světelného kuželu. Kužel bude na našich TSD vypadat vždy stejně.
Tento fakt má velkou důležitost. Představte si různé pozorovatele, kteří se všichni navzájem míjejí v jistém bodě času a prostoru. Většinou se navzájem neshodnou, kdy a kde se různé události odehrávaly a budou odehrávat. Nicméně, pokud vytvoříme světelný kužel se středem v bodě, kde se míjejí, všichni se shodnou na tom, které události jsou uvnitř a které vně kuželu. Bez ohledu na souřadné soustavy všech pozorovatelů platí pravidlo : (1) jediné události, které může kdokoliv z těchto pozorovatelů ovlivnit leží v horní polovině světelného kuželu; (2) jediné události, o kterých se kterýkoliv z pozorovatelů může dozvědět, leží v dolní polovině světelného kuželu.
Tyto znalosti nyní uplatníme pro pozorovatele a události na diagramu 2-8. Jak vidíte, událost označená hvězdičkou leží vně světelného kuželu. Díky tomu, přestože pro pozorovatele O se událost stala v minulosti vzhledem k toku času (t = 0), o této události se v tomto okamžiku nemůže dozvědět. Podobně, ačkoliv vůči pozorovateli O´ se událost teprve stane (v budoucnosti), nemůže a nebude moci ji nijak ovlivnit. V podstatě, bez ohledu na to kdy, kde, jak atd. se událost odehrála, ani jeden z pozorovatelů ji v době míjení se ani nezaregistruje, ani ji nijak neovlivní. Dopracováváme se k závěru naší otázky, proč to, že dva pozorovatelé, kteří se míjejí, mají různou představu o jisté události (pro jednoho je v jeho minulosti a pro druhého v budoucnosti), nevyvolá neřešitelný paradox : kdykoliv se jeví, že jeden pozorovatel při míjení druhého má jistou událost ve své minulosti a druhý tutéž událost ve své budoucnosti, potom tato událost se vždy nachází vně světelného kuželu se středem v bodě míjení a nemůže dojít k neřešitelnému paradoxu.
Ale neobsahuje tento relativistický obrázek vesmíru stále jakousi dvojznačnost konceptu minulosti a budoucnosti ? Filozoficky snad, ale fyzikálně ne. Jediná dvojznačnost, o které se lze dovědět, je ta, když se díváme na celý časoprostorový diagram najednou. Pokud byste byl jeden z pozorovatelů, který vidí prostor a čas „reálně“, a jiný pozorovatel by vás míjel, veškerý obraz časoprostru by byl obsažen pouze v dolní polovině světelného kuželu. Pokud jistý čas počkáte, může se vám povést shromáždit všechny informace ze všech událostí, které se odehrávaly v době, kdy jste míjel jiného pozorovatele. Z této informace můžete sestavit celý TSD a potom narazíte na jistou dvojznačnost. Ovšem v době, kdy se vám to povede, nebude tato dvojznačnost, o kterou se nám jedná, již dávno existovat. Jinak řečeno, tato dvojznačnost nemůže ve skutečnosti nikdy hrát roli v jisté fyzikální situaci.
Tato třetí kapitola naplňuje celý záměr tohoto článku a to spojení teorie relativity s (hypotetickými) teoriemi cestování rychleji než světlo (tzv. FTL - Faster Then Light - cestování). Nejprve probereme hlavní problémy, které z FTL plynou, jejich aplikování na různých FTL konceptech a nakonec aplikování toho všeho na FTL cestování, které se vyskytuje ve Star Treku (tedy Warp).
Než začneme probírat význam FTL, rád bych připomněl, že téměř veškerý časoprostor, ve kterém chceme cestovat, je nádherně „plochý“. Pro ty, co nestudovali Obecnou teorii relativity, to znamená, že na definici prostoru stačí pouze Speciální teorie relativity a není třeba se uchylovat k definicím v Obecné teorii (které začínají platit, pokud je přítomno gravitační pole). Zdroje gravitace jsou relativně řídce rozmístěné a vzdálené od sebe, a i pokud kolem nějakého běžného zdroje cestujete, zásadně nenaruší naši plochou časoprostorovou aproximaci. Je ovšem třeba připomenout, že některé koncepty FTL jsou přímo založené na neplochém modelu časoprostoru; nicméně, téměř u všech lze tento neplochý prostor aproximovat do prostoru plochého.
Pro všechny účely můžeme FTL cestování definovat jednotně : představte si pozorovatele, který cestuje z bodu A do bodu B. Ve stejné době, kdy pozorovatel opouští bod A, z tohoto bodu je vyslán světelný paprsek směrem k bodu B. Toto světlo cestuje v plochém časoprostoru bez jakýchkoliv vlivů, které by světlo způsobilo na cestujícího pozorovatele nebo obráceně. Pokud pozorovatel dorazí do bodu B tak, že zahlédne přílet paprsku do tohoto bodu, může říci, že „cestoval rychleji než světlo“. V této definici nezáleží na tom, kde se pozorovatel nachází během cesty, stejnětak, pokud se k pohonu lodi pozorovatele použije nějakého zkreslení časoprostru a loď sama se rychleji než c nepohybuje, pozorovatel stále cestuje rychleji než světlo, které se pohybuje v plochém, FTL pohonem nijak nezkresleném, časoprostoru. Tento cestovatel tedy také odpovídá základní definici FTL cestování.
V paměti na tuto základní definici se dále zaměříme na problémy, které s sebou FTL cestování přináší.
V této části se budeme věnovat prvnímu problému (a v některých FTL konceptech také jedinému), kterému se musí věnovat všichni ti, kteří se FTL cestováním věnují. Jak si vzpomínáte na kapitolu 1, rychlost světla je gigantická a prakticky nedosažitelná, natož překročitelná. Různé koncepty FTL řeší tento problém různě, ale nyní se jim budeme zabývat obecně.
Na začátek si představte dva pozorovatele, A a B. Nechť je A zde na Zemi a je v klidu. B bude vzhledem k A zrychlovat a směřovat k nějaké vzdálené hvězdě. Pokud rychlost B bude 80% rychlosti světla vzhledem k A, potom konstanta c bude pro něj 1,666… = 1/0,6. Z pohledu pozorovatele A se tedy čas pro B zpomaluje a jeho délka ve směru pohybu se zkracuje o faktor 0,6. Pokud by B cestoval rychlostí 0,9c, tento faktor by byl 0,436 a při 0,99c by byl přibližně 0,14. Čím se rychlost více blíží rychlosti světla, tento faktor se stále zmenšuje k nule a čas pro B se stává nekonečně pomalý a A uvidí jeho délku ve směru pohybu stávat se nekonečně malou.
Navíc, pokud je rychlost B 0,8c vzhledem k A, potom se pozorovateli A bude zdát, že energie pozorovatele B se zvětšuje o násobek konstanty c, vzhledem k jeho energii v klidu (viz vzorec v kapitole 1) :
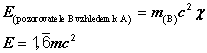
Pro rychlosti 0,9c a 0,99c je tento faktor c přibližně 2,3; respektive 7,1. Při přibližování se rychlosti světla se bude pozorovateli A zdát energie B stávat nekonečně velká.
Z pohledu A nebude schopen pozorovatel B dosáhnout rychlosti světla bez toho, aby zastavil běh svého času, „srazil“ se v nic ve směru pohybu a nabyl nekonečné energie.
Nyní se na celou záležitost podíváme z pohledu B, takže budeme předpokládat, že se nachází v klidu. Budeme dále předpokládat, že Slunce, ostatní planety a blízké hvězdy se vzhledem k Zemi relativně nepohybují - všechno toto bude tedy ve stejné vztažné soustavě. Jak víme, B míjí Zemi a směřuje k nějaké blízké hvězdě. Z jeho pohledu ovšem Země, Slunce, planety, hvězdy atd. se sami pohybují vysokou relativistickou rychlostí vzhledem k němu opačným směrem. Takže pro něj se zdá, že se čas na Zemi zpomaluje, energie všech objektů se zvyšuje a jejich vzájemná vzdálenost ve směru pohybu se zmenšuje, stejně jako jejich délka.
Nyní si uvědomme vzdálenost Země a hvězdy, ke které B směřuje. Z pohledu pozorovatele B se tato vzdálenost stává nekonečně malá a může se k ní tedy dostat v prakticky nulovém čase. (Toto vysvětluje to, proč se pozorovateli A zdá, že se čas pro B zastavuje, když jeho rychlost je téměř c. B neshledává na svém běhu času nic zvláštního, ale vzdálenost v jeho vztažné soustavě, kterou musí urazit, je velmi malá.) Pokud (v soustavě pozorovatele B) se vzdálenost zkracuje na nulu a jeho rychlost vzhledem k A se přibližuje rychlosti světla, je tedy schopen se tam dostat okamžitě, protože z pohledu B je rychlost c nejvyšší dosažitelná rychlost.
Ze všech pohledů se tedy zdá, že rychlosti světla nelze dosáhnout, natož překročit. Toto se nazývá „bariéra rychlosti světla“, ale ve většině konceptů FTL je na tento problém myšleno (jak uvidíme dále). Nicméně, řešení dalšího problému není již tak jednoduché a navíc, tento problém není u velké části laické znám.
V této kapitole rozebereme problém související s FTL cestováním, o kterém se ne vždy uvažuje. Tento problém vyvolává neschopnost zabránit příčinnosti v různých vztažných soustavách. Přestože toto samotné nezabraňuje existenci FTL cestování, za jistých podmínek to může způsobit vznik neřešitelných paradoxů, které by činili FTL cestování logicky si odporující. Začnu tedy probírat význam příčinnosti a problémů neřešitelných paradoxů. Ukáži také, jak jakýkoliv typ FTL cestování může porušit princip příčinnosti. A konečně ukáži, jak takový princip FTL, který nemá tzv. speciální provize, může způsobit vznik neřešitelného paradoxu.
Princip příčinnosti lze definovat velmi jednoduše. Podle příčinnosti, pokud existuje nějaký efekt, který byl důsledkem nějakého procesu, potom tento proces musí předcházet tomuto efektu. Pokud se tedy pro nějakého pozorovatele v nějaké vztažné soustavě efekt odehraje dříve než jeho příčina, potom je příčinnost pro tohoto pozorovatele porušena. Vzpomalte na výklad v první části kapitoly 1, kde bylo vysvětleno, jak se události odehrávají ve vztažné soustavě. Bylo zde uvedeno, že pokud hovoříme o pořadí událostí nebo příčin v nějaké soustavě, máme vždy na mysli jejich skutečné pořadí a ne pořadí, v jakém byly viděny. To lze dokumentovat na tom, že nelze nejprve uvidět světelný obraz efektu a poté teprve světelný obraz příčiny. To lze jen v případě, že je efekt mnohem blíže než příčina. Poté ale mohu vzít v potaz dobu, kterou světlo potřebovalo na překonání dané vzdálenosti a mohu opět určit přesné a skutečné pořadí všech událostí a zjistit tak, jestli se zde opravdu nachází jakési porušení příčinnosti nebo ne (pochopitelně, že vždy dojdu k záporné odpovědi). Za skutečné porušení příčinnosti budeme tedy dále považovat pouze skutečný proces, nikoliv jen jakýsi „trik“ způsobený konečnou rychlostí světla.
Mnozí se také mohou domnívat, že ani existence porušení příčinnosti sama neporušuje logiku. Tato myšlenka se zdá správná (protože to, že efekt následuje příčinu, je jen zažitý model chování, který je nám „vtloukán horem dolem“ od doby jednobuněčných živočichů až po teď, protože na Zemi toto pravidlo pochopitelně nic neporušuje), protože nevytváří samo si odporující situace. Neřešitelný paradox je ovšem samo si odporující situace, tedy situace, která si sama logicky zabraňuje ve své existenci. Pokud tedy někdo připustí, že určitý souhrn okolností může vyvolat neřešitelný paradox, potom tyto okolnosti musí byl logicky neuskutečnitelné.
Pro podrobnější vysvětlení se budu odvolávat na diagram 2-8 v kapitole 2 tohoto článku, který ukazuje dva míjící se pozorovatele. Tento diagram je zde okopírován a označen 5-1 :
Diagram 5-1
Počátek s.s. označuje bod, kde v prostoru a v čase jsou oba pozorovatelé těsně vedle sebe (matematicky řečeno jsou teď jeden pozorovatel). Osy x´ a t´ označují vztažnou soustavu pozorovatele O´ a osy x a t vztažnou soustavu pozorovatele O. Systém O bude v klidu a pozorovatel O´ bude pozorovatele O míjet relativistickou rychlostí. Jak vidíte na dvou různých soustavách souřadnic, oba pozorovatelé měří svůj čas a prostor jinak. Nyní se opět zaměříme na událost označenou hvězdičkou. Pomineme osy x a t a zaměříme se jen na systém O´. V tomto systému je tato událost nad osou x´. Pokud by se pozorovatel O´ mohl podívat doleva nebo doprava a vidět celou svou prostorovou osu zároveň, musel by na vyskytnutí se události * chvíli čekat. Při zaměření se na systém O zjistíme, že tato událost je pod osou x a pozorovatel O ji již zaznamenal před tím, než se minul s druhým pozorovatelem.
V normálním případě toto nečiní žádný problém, protože si přes diagram můžeme nakreslit světelný kužel (viz kapitola 2.6) se středem v počátku s.s. Událost * se ocitne vně kuželu a dokud nějaký signál z této události nemůže letět rychleji než světlo, bude pro oba pozorovatele nemožné o události v tomto časovém bodě vědět nebo ji nějak ovlivnit. Přestože je tedy v minulosti jednoho pozorovatele, nemůže o ní vědět a přestože je v budoucnosti druhého pozorovatele, nemůže ji ovlivnit. Toto je způsob, jak se relativita sama chrání proti porušení příčinnosti.
Jaký by mělo vliv FTL cestování na tento diagram ? Při míjení se se událost * ve vztažné soustavě pozorovatele O´ ještě nestala. Mohl by ale z počátku vyslat dostatečně rychlý FTL signál, který by ovlivnil událost *. Nicméně, ve vztažné soustavě O se událost * již odehrála před tím, než se oba pozorovatelé minuli. To znamená, že v soustavě O by událost „O´ vyslal signál, který ovlivnil událost *“ následovala událost, kterou ovlivnila, tedy *. Pro pozorovatele O tedy efekt předchází příčinu. Proto FTL signál, který cestuje v soustavě O´ poruší princip příčinnosti v soustavě O. Podobně, protože * se již odehrála v soustavě O, když se pozorovatelé minuli, potom v jeho soustavě FTL signál mohl být vyslán z * a říci mu o existenci události * v době, kdy se pozorovatelé minuli. Nicméně, pro O´ by událost „pozorovatel O se dozvěděl o události * v době, kdy jsme se míjeli“ předcházela samotné události *. Proto FTL signál ve vztažné soustavě O poruší princip příčinnosti v soustavě O´.
Zkráceně, pro každý FTL signál vyslaný v jisté vztažné soustavě lze najít jinou vztažnou soustavu, ve které tento signál vlastně cestoval zpět v čase, čímž pochopitelně vyvolal porušení principu příčinnosti.
Připomínám, že ve výkladu výše jsem nikde neuvedl, jak signál překoná vzdálenost mezi počátkem s.s. a *, ani jsem netrval na tom, že signál se nacházel v „našem“ vesmíru (viz naše definice FTL cestování). Jediné dvě podmínky byly : (1) vyslání a přijímání signálu probíhalo v „našem“ vesmíru a (2) časoprostor mezi počátkem a * byl plochý (tedy, lze ho úplně popsat časoprostorovými diagramy speciální teorie relativity). Jak jsem již uvedl, některé již existující FTL koncepty mohou porušovat druhou podmínku, ale o tom až později. Jak také uvidíme, porušení příčinnosti je důsledkem všech FTL konceptů, ale nejedná se o samo si odporující situaci.
Kromě logicky řešitelného porušení příčinnosti může FTL cestování vyvolat tzv. neřešitelný paradox (tj. situaci, která si sama zabraňuje ve vlastní existenci).
Použijeme opět podobného příkladu, jaký je zaznačen na diagramu 5-1. Místo toho, aby pozorovatel O´ vysílal v době, kdy se míjí s druhým pozorovatelem, FTL signál, který nějak pozmění událost *, řekněme, že vystřelí kulku, která opět letí rychlostí větší než c. Tato kulka může zabít někoho několik světelných let vzdáleného jen v několika hodinách (například) ve vztažné soustavě O´. Řekněme tedy, že pozorovatel vyšle tuto kulku těsně po tom, co se minul s O. Smrt oběti může být potom zaznačena jako událost *. Pro pozorovatele O je oběť v době, kdy se míjí s O´ už mrtvá (událost * se pro něj již stala). Proto jiný pozorovatel, který se v soustavě O nepohybuje a stál vedle oběti, když byla zastřelena, může vyslat FTL signál ihned po smrti oběti a ten může O odchytit ještě před tím, než se mine s O´. Pozorovatel O se tak dozví, že O´ vystřelí na oběť poté, co se minou.
Pro zdůraznění toho, na co chci poukázat, řekněme, že onen signál, který dorazil k O od svědka bude fotografie nebo dokonce videozáznam těla oběti. Tudíž má O důkaz o smrti oběti před tím, než O´ vystřelil kulku (jasné porušení příčinnosti). Nicméně, teď se O může rozhodnout, že zabrání pozorovateli O´, aby kulku vystřelil. Pokud není ale kulka vystřelena a oběť nikdy nezahyne, potom proč (a vůbec jak) mohl být vyslán video-signál s dokumentací mrtvého těla oběti. A navíc, O má onen videozáznam!
Na závěr lze říci, že je to smrt oběti, která způsobí to, že O zabrání smrti oběti. A to je jednoznačně logicky nevysvětlitelná a samo si odporující situace. Pokud v FTL mechanizmech nejsou vytvořeny jakési speciální provize (viz dále), FTL cestování nezpůsobí jen sice matoucí, ale řešitelné porušení příčinnosti, ale také neřešitelné paradoxy.
V tomto bodě bych dále uvedl přesný seznam událostí, které se musí odehrát v našem „příkladu s FTL kulkou“, aby vznikl neřešitelný paradox. To nám pomůže v další diskuzi o FTL cestování.
Seznam událostí s komentáři
1. Těsně poté, co se O a O´ míjejí (tak, jak jsou zakresleni na diagramu 5-1), O´ použije nějakou metodu na vyslání FTL kulky ve své vztažné soustavě. Událost „O a O´ se míjejí“ bude označována „míjení se“.
2. Kulka zastřelí oběť, jejíž smrt je na diagramu 5-1 zaznačena jako událost * . Tato událost se stane po míjení se ve vztažné soustavě O´, ale před touže událostí ve vztažné soustavě O.
3. Třetí pozorovatel, který viděl zastřelení oběti a je tudíž svědek, je vzhledem k O v klidu (jeho vztažná soustava se shoduje s O), takže událost míjení se se odehraje po tom, co byla oběť zastřelena. Tímto se třetí pozorovatel stává svědkem efektu, jehož příčina se odehraje v budoucnosti - má informaci o budoucí události ve své vztažné soustavě.
4. Třetí pozorovatel vysílá informaci o budoucnosti k pozorovateli O pomocí FTL signálu a v jeho vztažné soustavě může pozorovatel O dostat tuto informaci před událostí míjení se (a tedy před tím, než byla FTL kulka vystřelena).
5. O přijme informaci a dozví se o smrti oběti před tím, než byla kulka vystřelena. Ví tedy i o tom, že kulka bude vystřelena v jeho vlastní budoucnosti.
6. O použije tuto informaci, aby zabránil O´ ve vystřelení kulky, čímž vytvoří neřešitelný paradox.
Je důležité připomenout, že největší zádrhel tohoto paradoxu nepochází ze samotného používání FTL, ale ze vztahu mezi dvěma naprosto běžnými vztažnými soustavami dvou různých pozorovatelů, kteří sami nikdy necestovali rychleji než světlo.
Poté, co jsme probrali dva hlavní problémy spojené s FTL cestováním, je naši úkolem podívat se na různé FTL koncepty a jejich postoj k těmto problémům.
V této části se budeme zabývat názory na překonání těchto problémů. Mnoho z vás už jistě slyšelo o různých nápadech na překonání problému bariéry rychlosti světla. Například, můžeme cestovat v nějakém jiném, paralelním „prostoru“, kde bychom nebyli obtěžování tímto problémem. Nicméně, tyto vize již zcela neřeší další dva hlavní problémy, ba naopak. Ve skutečnosti, už na překonání druhého problému budeme potřebovat ony speciální provize (které by byly jaksi „zhůry dány“).
Naše diskuze bude mít tedy následující formát : nejprve představím některé koncepty dovolující FTL cestování. Ukážeme si, jak každý z nich překonává bariéru rychlosti světla, a vysvětlím, jak (bez speciálních provizí) žádný z nich nemůže překonat druhý problém - vytváření neřešitelných paradoxů. Nakonec představím některé speciální provize (sahající za pojetí FTL konceptů) a způsob, jak je spojit s některými z FTL konceptů, aby byl i druhý problém vyřešen.
Tachyony jsou hypotetické/teoretické elementární částice (na úrovni např. elektronu), které se dovedou pohybovat rychleji než světlo. Jejich koncept se pokouší řešit problém potřeby nekonečné energie na to, aby částice dosáhla rychlosti světla. Toho bylo dosaženo již zvláštními charakteristikami částice.
Nejprve si vzpomeňme, že můžeme zapsat energii a moment částice o hmotnosti m rovností :
![]()
kde E je energie, p je hybnost, c rychlost světla, v rychlost částice a c je definována vzorcem :

Odtud můžeme napsat (pc)/E = v/c, což je větší než 1 pokud v je větší než c. Pro FTL částici lze tedy zapsat :
![]()
Protože ovšem můžeme vyjádřit druhou mocninu energie i takto :
![]()
zjistíme, že jediný způsob, jak učinit, aby platilo E2 < p2c2, je to, aby druhá mocnina hmotnosti byla negativní (protože poté se výraz m2c4 odčítá od výrazu p2c2). Hmotnost by potom byla druhá odmocnina z negativního čísla, čímž by nám vyšlo komplexní, imaginární číslo. Hmotnost tachyonu je tedy imaginární. Dále, z rovnice pro c zjistíme, že je také imaginární, pokud je v větší než c. To znamená, že z rovnice E = mc2c vyplývá, že energie by bylo reálné, záporné číslo (protože násobíme dvě imaginární čísla - m a c). Totéž by platilo pro hybnost.
Poslední zajímavou vlastností tachyonů, o které se zmíním, je to, že pokud chceme zvýšit jejich rychlost (tedy zvyšovat druhou mocninu hybnosti), musíme zvýšit druhou mocninu jeho energie. To lze jen tam, že již negativní energie se stane ještě více negativní. Tedy, když tachyon ztrácí energii, zrychluje se. Jediný důsledek je ten, že pokud nabitý tachyon existuje, vydával by tzv. Cherenkovovo záření. To by mu ale ubíralo energii a zrychlovalo - neustále by vydával více a více energie, čímž by se více a více zrychloval a tak neustále dokola. Neutrální tachyony (bez náboje) by to ovšem nedělaly.
V každém případě můžeme uvažovat o tom, že tachyony existují a vždy se pohybují rychleji než světlo. Nikdy nemusí překročit bariéru rychlostí světla a nikdy tudíž nemají nekonečně energie (ovšem jejich energie je negativní). Stále ovšem neřeší druhý problém - pokud by je bylo možno použít k FTL komunikaci, mohly by způsobit neřešitelné paradoxy stejně, jako naše kulka v příkladu.
Pro zodpovězení otázky využití tachyonů v FTL komunikaci nám nezbývá, než na výše uvedené rovnice uplatnit kvantovou mechaniku. Tím dojdeme k závěru, že buď (1) nelze tachyony lokalizovat, nebo (2) samotný efekt tachyonů se nemůže pohybovat rychleji než světlo. V obou případech je nelze použít k vytvoření FTL signálu.
Třetí možnost spočívá v tom, že tachyony mohou existovat, i když pomocí nich nemůžeme vyslat FTL signál. Spočívá to v tom, že nelze rozlišit, kdy tachyony vysíláme a kdy přijímáme. Na diagramu 5-1 to lze vysvětlit takto : ve vztažné soustavě O lze tachyony vyslat „z“ * „do“ počátku. Nicméně, dokud nemůžete rozlišit přijímač a vysílač, potom to může pozorovatel O´ interpretovat tak, že lze tachyony vyslat „z“ počátku „do“ *. Nikomu z nich se potom nebude zdát, že se tachyony vrací v čase. Protože neexistuje způsob, jak vyslat zprávu (a tudíž nelze určit, odkud byly tachyony vyslány), nelze toto nazývat FTL komunikace.
Přesto mohou tachyony existovat, ač je nemůžeme nijak využít, bez toho, aby způsobovaly nějaké problémy. Proto lze o tachyonech říci pravdivě jedno z následujících :
1. Tachyony neexistují,
2. Tachyony existují, ale nelze je použít pro vyslání FTL signálu, nebo
3. Tachyony existují a lze je použít k vysílání FTL signálů, ale nějaká speciální provize zabraní tomu, aby tak vznikaly neřešitelné paradoxy.
Další postupy, hojně používané jako FTL metody hlavně v science fiction. Dají se shrnout v podstatě do toho, že např. loď může použít speciální pole nebo cestovat v jiném prostoru nebo se přemisťovat po osách, které již nejsou definovány čtyřrozměrným časoprostorem - vždy tedy tak, aby ji nelimitovaly zákony „našeho“ vesmíru.
Jak můžeme hned vidět, tento koncept sám osobě řeší problém bariéry rychlosti světla, která se nepřekoná, ale obejde. Nicméně, s neřešitelnými paradoxy si stále nedovede dobře poradit.
Protože FTL cestovatel nebo signál, který cestuje pomocí tohoto konceptu, sice opustí království naší fyziky, ale vztahy mezi dvěma nebo více pozorovateli (jako byli např. naši O a O´), kteří zůstanou v království naší fyziky, se nezmění, argumenty pro vytváření neřešitelných paradoxů nepřestanou platit (pokud nebudou platit nějaké speciální provize). Jak jsme si již řekli, tyto argumenty jsou založeny na vztazích mezi právě těmi pozorovateli, kteří samotní necestují rychleji než světlo (a tudíž nikdy neopustí království naší fyziky).
Jak vidíme, dokud se nevytvoří nějaké speciální provize, tyto metody mohou vytvářet neřešitelné paradoxy.
Další koncept známý mezi fanoušky sci-fi je založený na tom, že by bylo možno přiblížit dva (popř. více) bodů prostoru tak, ze by se vzdálenost mezi nimi dala překonat rychleji, aniž bychom se vlastně pohybovali rychleji než světlo. Tento postup ovšem stále odpovídá definici FTL cestování z kapitoly 3.
Nejznámější je přirovnání k listu plochého papíru. Řekněme, že se chcete dostat z bodu A na povrchu papíru do bodu B opět někde na stejném povrchu papíru (omezíme se tedy na trojrozměrný časoprostor). Abyste tak učinili, budete prostě papír ohýbat, skládat, kroutit atd. až dostanete oba body si co nejblíže k sobě. Teď už stačí jen málo času a energie na překonání této vzdálenosti malou relativistickou rychlostí.
Tento problém je postaven stejně jako předchozí v kapitole 6.2 - řeší problém bariéry rychlosti světla, vytváření neřešitelných paradoxů neřeší.
Poslední koncept, na který se zaměříme před tím, než přikročíme ke speciálním provizím, lze souhrnně nazvat časoprostorové manipulace. Nápad spočívá v tom, že pozměníme vztah mezi časem a prostorem v jisté oblasti tak, že limitace rychlostí světla přestane platit. To se většinou omezuje na království Obecné teorie relativity.
Existují dva různé druhy časoprostorových manipulací. První lze nazvat „místní“, protože se jedná o ovlivnění časoprostoru kolem vaší lodi (nebo toho, v čem se pohybujete). Příklad tohoto druhu FTL cestování lze nalézt ve spisech profesora Miguela Alcubierreho z Waleské Univerzity (který nedávno opět rozvířil klidné vody fyziků - tento spis si lze přečíst přes World Wide Web na URL adrese https://www.astro.cf.ac.uk/groups/relativity/papers/abstracts/miguel94a.html). Alcubierre popisuje postup, při kterém se použije „exotické hmoty“ (hmota s zvláštními vlastnostmi, která může, ale také nemusí existovat) na změnu časoprostoru v okolí lodi podle pravidel Obecné teorie relativity. Tento změněný časoprostor nejen že se chová tak, že čas ubíhá na lodi stále tak, jako by byla „v klidu“ (ve své původní vztažné soustavě), ale „pohání“ loď libovolně vysokou rychlostí vzhledem ke své vztažné soustavě před aktivováním tohoto FTL pohonu.
Druhý typ tohoto konceptu je „nelokální“ a ovlivňuje časoprostor minimálně startovní a cílovou pozici (a pravděpodobně všechny body mezi). Základním příkladem tohoto je červí díra. Mnozí lidé si ovšem myslí, že červí díra je jen výmysl autorů science fiction, A.C.Clarka nebo Star Treku - ne, červí díra je další koncept Obecné teorie relativity. Opět je použita „exotická hmota“, ale časoprostor je ovlivněn tak, že dva jeho body jsou spojeny. Můžete vletět do jednoho otvoru červí díry a opustit ji druhým, velmi vzdáleným otvorem, což odpovídá naší definici FTL cestování.
Pokud usuzujete správně, oba koncepty (pokud neobsahují speciální provize), řeší jen první problém (bariéra rychlosti světla), neřešitelné paradoxy se ovšem stále mohou objevit.
Zkráceně lze říci, že ani jeden z výše popsaných FTL konceptů neřeší problém neřešitelných paradoxů. Nicméně, všude bylo připomínáno, že i tento druhý problém by se dal vyřešit za použití speciálních provizí. Definicí takových provizí se nyní budeme zabývat. Speciální provize není nic, co již bylo zmíněno (používání různých polí, hmot, „kroucení“ vesmíru atd.), ale předpokládá se, že je to vlastnost samotného vesmíru zabránit vytváření neřešitelných paradoxů. Pokud by totiž někde nějaký takový paradox vznikl, určitě by se nejednalo jen o jakousi lokální záležitost, ale pokud by byl vesmír jakýsi počítač, pak by se určitě „zaselk“.
Existují čtyři typy provizí, ale než je probereme podrobně, podíváme se na základní myšlenku všech. Pokud si vzpomenete na příklad s FTL kulkou, skládal se ze série událostí, které se všechny podílely na vzniku paradoxu. Speciální provize musí nutně zaručit, že alespoň jedna z těchto událostí se nestane (a pokud možno to nebude FTL cestování), čímž se zabrání vytvoření paradoxu. U první a druhé provize se nebudou na FTL cestování klást podmínky a jakékoliv události (i ty, které s FTL cestováním nesouvisí) mohou být „zakázány“. Další dvě kladou omezení FTL cestování tak, aby nezpůsobovalo vznik paradoxů.
V této první provizi se nebude jednat anitak o zabránění nějaké události, ale o její „přesunutí“ z nebo do jiného (paralelního) vesmíru nebo reality. Například řekněme, že pozorovatel O právě získal informaci o smrti oběti v události * a čeká, aby mohl zabránit O´ ve vystřelení FTL kulky. Nicméně, předtím, než to může provést je přenesen do paralelního vesmíru, kde může O´ zabránit ve vystřelení kulky. Neřešitelný paradox je tak vyřešen, protože informace o mrtvé oběti z * nepochází z téhož vesmíru, kde on (O) zastavil O´. Místo toho si tuto informaci přinesl z velmi podobného paralelního vesmíru, kde je oběť mrtvá, zatímco zde ne.
Podobný proces lze provést s jakoukoliv ze všech šesti událostí. Dokud lze jednu z těchto událostí přenést z nebo do paralelního vesmíru, nehrozí nikdy vznik paradoxu (a abychom teorii dokončili, pro každé nebezpečí vzniku neřešitelného paradoxu vznikne nový paralelní vesmír). Je nutno také připomenout, že tato provize může ochránit všechny koncepty FTL cestování, o kterých jsme hovořili.
Druhou provizi lze nazvat „důsledková ochrana“, protože se může jednat o jakýsi vnitřní mechanizmus vesmíru, který učiní to, že alespoň jedna událost z našeho seznamu se prostě nestane.
Příklad takového mechanizmu můžeme najít za pomocí kvantové mechaniky. (Teorie Stephena Hawkinga nazývaná „chronologická protekce dohadu“ je založena na tom, že tam venku je jakási jury, která neustále rozhoduje o lineárním toku času.) Ve kvantové mechanice nepřemýšlíme o tom, zda se v jisté době do budoucna jistá událost stane nebo ne, na základě toho, co víme v přítomnosti. Místo toho zvažujeme pravděpodobnost události (nebo řetězce událostí). Jedna forma důsledkové ochrany může být taková, že samotná kvantová mechanika zabraňuje vzniku neřešitelných paradoxů a to tím, že pravděpodobnost souhry všech událostí v našem příkladu je prakticky nulová.
Kvantová mechanika by mohla zasáhnout např. tak, že pozorovatel O´ nebude schopen vyslat FTL kulku, třeba protože se mu pokazí zbraň, čímž paradox nevznikne. Pokud se O´ podaří vystřelit kulku, pravděpodobně mine. Nejpravděpodobnější je ovšem to, že vše proběhne stejně, ale pozorovatel O nebude schopen zabránit ve vyslání kulky. V každém případě kvantová mechanika zabezpečí, že se jedna z událostí nemusí neuskutečnit, protože pravděpodobnost uskutečnění všech je prakticky nulová.
Tato provize potřebuje existenci nějakého mechanizmu ve vesmíru a stejně jako předchozí na ni lze aplikovat všechny koncepty FTL cestování.
Tato provize se podobá předchozí, je ale trochu pozměněná a její mechanizmus se speciálně týká FTL cestování tak, že zabrání některé FTL cestě nebo vysílání zpráv tak, aby nedošlo k neřešitelnému paradoxu. V našem příkladu jsme měli dvě FTL cesty (FTL kulka a FTL zpráva). Pro ilustraci si probereme obě možnosti. V první z nich je povoleno O´ pozorovateli vyslat FTL kulku a zabít oběť, ale svědkovi se nepodaří poslat FTL zprávu pozorovateli O. V druhé verzi se těsně před událostí * rozhodne svědek zaslat O nějakou FTL zprávu a to do té doby, než by kukla zabila oběť (vysílač se nemůže pokazit jen tak sám od sebe - provize nesmějí porušovat fyzikální zákony). Proto se nesmí povolit, aby byla FTL kulka zabila oběť.
Takže jak vlastně ony provize v obou případech pracují ? Pokud je třeba zabránit všem paradoxům jen tak, že „zakazujeme“ jednotlivé FTL lety, musí se použit jistý algoritmus. Musíme probrat obě situace podrobně za pomoci TSD.

Diagram 6-1
V tomto diagramu vidíme událost, kdy je FTL kulka vyslána z události míjení se (z počátku) a je „přijata“ obětí v události *. Na diagramu jsou nově také části světelného kužele (čárkované čáry). Jeden je horní polovina světelného kužele se středem v události * a druhý je dolní polovina světelného kužele se středem v počátku s.s. Uvnitř prvního se nachází všechny události, které může pozorovatel (např. třetí pozorovatel z našeho příkladu) ovlivnit, aniž by používal FTL. Všichni pozorovatelé souhlasí, že všechny události v této výseči se odehrají jistý čas po * (viz kapitola 2.6). Podobně, dolní část kuželu se středem v O obsahuje všechny události, které bez pomoci FTL mohou ovlivnit pozorovatele O a O´ (což je mj. událost vyslání kulky). Pokud tedy žádný FTL signál/cestovatel nemůže opustit jako událost horní část kuželu * a dorazit do dolní části kuželu O, nemůže vzniknout žádný neřešitelný paradox.
Pro FTL cestování lze tedy vytvořit následující provizi : pokud je FTL signál vysílán jako událost A a přijímán jako událost B, nesmí být možno pro žádnou informaci, aby byla vyslána jako událost v horní (budoucí) části světelného kuželu A a přijata jako událost v dolní (minulostní) části světelného kuželu B. Pokud by tento univerzální zákaz platil, nemohly by vznikat žádné neřešitelné paradoxy.
Nicméně, věci se mohou začít zdát o něco komplikovanější, pokud se na celou situaci podíváme z pohledu O, tedy ze vztažné soustavy O (která je také vztažnou soustavou třetího pozorovatele). V této soustavě, poté, co se třetí pozorovatel stane svědkem smrti oběti v *, událost „kulka byla vyslána“ se ještě neodehrála. Mohl by totiž tvrdit, že nebyl vyslán žádný FTL signál, který by bránil v tom, aby vyslal svůj FTL signál O. Problém je v tom, že ve skutečnosti se již stal svědkem důsledku FTL kulky, která byla vyslána (i když ne v jeho vztažné soustavě). Tedy jakýkoliv FTL signál, který by se snažil zaslat O, by ve skutečnosti vyslat nemohl.
Co ovšem v druhém případě (kdy se třetí pozorovatel rozhodne vysílat FTL zprávu O těsně před tím, než se stane svědkem zabití oběti) ? K tomu musíme použít druhý diagram.
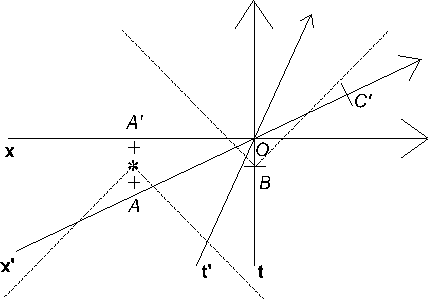
Diagram 6-2
Tento diagram je o něco komplikovanější. Bod A představuje událost, kdy třetí pozorovatel začal vysílat svou FTL zprávu, a bod A´ událost, kdy přestal vysílat. Bod B ukazuje na událost, kdy pozorovatel O zachytil poslední zprávu třetího pozorovatele (vyslanou z A´). Dále je na diagramu nakresleny opět dvě poloviny světelného kuželu (tentokráte ale obráceně). Jak bylo uvedeno výše, O´ nebude schopen vyslat kulku v počátku s.s. (který je v horní polovině kuželu se středem v B), aby byla „přijata“ obětí v * (což je v dolní polovině kuželu se středem v A´). Podle tohoto tedy kulka nikdy neopustí bod O v případě, že třetí pozorovatel vysílá FTL signály k O, takže třetí pozorovatel nikdy O neoznámí o smrti oběti.
Na otázku „Která z obou variant se skutečně stala ?“ existuje jednoduchá odpověď „Je to opravdu úplně jedno.“ Opět se potvrzuje pravidlo, že pokud se nestane jen jedna událost, nedojde k vytvoření paradoxu.
A tak máme k dispozici provizi, která jednoduše zakazuje některé FTL cesty z důvodů jiných FTL cest. Přišli jsme na to, že nemusí existovat přesná odpověď na to, kterou cestu zakázat, a přesto tato provize zabezpečí, že všechny situace se stanou „samo se podporující“, a zabrání se vzniku neřešitelných paradoxů. Tato provize má jednoduchou a matematicky jasnou definici a není k ní potřeba nějaké „jury“, která vybírá, kterou událost nepovolit.
Poslední provize je opět částečně založena na předešlé. Tato provize také zakazuje jisté FTL signály, ale dělá to velmi specifickou a zajímavou cestou (není se třeba ptát, které FTL cesty povolit a které ne). Vysvětlím její funkci na příkladu. Při tom budu používat koncept „speciálního pole“ pro vytvoření „speciální vztažné soustavy“. Nicméně, není třeba disponovat takovýmto speciálním polem, pokud taková vztažná soustava existuje přirozeně. Používám tento koncept jen pro názornou ilustraci.
Představte si určitou část prostoru (řekněme několik kubických světelných let), která je naplněna nějakým polem. Nechť má toto pole nějakou zvláštní vztažnou soustavu. Řekněme, že v budoucnu toto pole objevíme a budeme umět měnit jeho strukturu nebo podobu. Poté, co dokončíme tento proces - přeformování pole, tzv. warping, bude mít toto pole velmi zvláštní vlastnosti. Pozorovatel uvnitř této warp-zóny může cestovat libovolnou rychlostí vzhledem k poli a jeho vztažná soustava bude vždy stejná, jakou má pole. To znamená, že osy x a t v TSD budou pro pozorovatele stejné jako pro pole, bez ohledu na rychlost pozorovatele. Jak jsme si řekli již dříve při probírání teorie relativity, vztažná soustava pozorovatele je závislá na jeho rychlosti vzhledem k objektům, které pozoruje. Nicméně, pro cestovatele v tomto warp-prostoru to již neplatí.
Představme si dva pozorovatele, A a B, kteří jsou na stejné pozici uvnitř warp-prostoru. Pozorovatel B zůstane v klidu, zatímco A zrychlí na vysokou relativistickou rychlost, uletí jistou vzdálenost a vrátí se k B. Za normálních podmínek zestárne pozorovatel B více než pozorovatel A (díky dilataci času). Pokud by ovšem A použil vlastnosti tohoto speciálního pole, nestalo by se tak a hodiny obou pozorovatelů by ukazovali stejně.
Řekněme, že všechny FTL lety se budou provádět v tomto poli (např. proto, že to v normálním prostoru díky bariéře rychlosti světla nepůjde). Jak se tedy odstraní neřešitelný paradox ? Vraťme se opět k našemu příkladu. Nyní si projdeme opět náš seznam událostí z kapitoly 5.3, jen tentokrát použijeme pro každou FTL cestu speciální pole.
Zde je tedy nový seznam :
(Stejně jako předtím), v době, kdy se pozorovatelé O a O´ míjejí, O´ vystřelí FTL kulku. Vztažná soustava speciálního pole se tedy stane také vztažnou soustavou kulky.
Kulka opět zabije oběť, a to po událostí míjení se ve vztažné soustavě O´ a před touto událostí v soustavě O.
Opět třetí pozorovatel (ve vztažné soustavě shodné s O) se stane svědkem zabití oběti a bude mít informaci o tom, co se stane v jeho soustavě v budoucnosti.
Dále ovšem už žádné „opět“ nebude. V původním seznamu byla událost 4 (svědek posílá O FTL signál) možná. V soustavě O (a třetího pozorovatele) mohla být informace poslána po smrti oběti (*) a před událostí míjení se. Nyní ovšem má informace vztažnou soustavu speciálního pole. To byla také soustava kulky a v té oběť zemře po tom, co byla vystřelena kulka. V soustavě zprávy je tedy již kulka vyslána a informace nemůže dorazit k O dřív, než po jejím vyslání.
Z pohledu třetího pozorovatele nemůže zprávu vyslat natolik rychle, aby dorazila k O před tím, než je kulka vyslána. Z pohledu O (a třetího pozorovatele) je možné vyslat jen ty FTL zprávy, které nedonesou nějakou informaci zpět v čase. To zabrání vzniku neřešitelného paradoxu.
Na závěr lze řící, že pokud by tato provize platila, FTL cestování by bylo možné jen v tomto poli, což by díky svým vlastnostem zabránilo vzniku paradoxu a navíc by pomohlo jednoduše překonat bariéru rychlosti světla. Tato provize lze také aplikovat na všechny FTL koncepty, ať už to jsou tachyony, teorie červích děr atd.
Jak již bylo řečeno v úvodu, v této části budou všechny námi vysvětlené provize aplikovány na to, co jsme mohli za více než 30 let existence Star Treku vidět a číst. Bylo by pochopitelně bláznivé předpokládat, že především autoři scénářů se měli čas všemi stránkami teorie relativity a FTL podrobně zabývat, ovšem i tak je úroveň vědeckého podání ve Star Treku velmi vysoká a především mnohem vyšší, než u všech jiných sci-fi (Star Trek totiž není science fiction, ale science reality). U románových děl je tato úroveň dokonce ještě vyšší. K celkově zvýšené úrovně v posledních 12 letech přispěly především přepracované „Bible“ Star Treku a hlavně Technický manuál pro spisovatele Star Treku (od pánů Sternbacha a Okudy), který právě tyto věci související s relativitou a FTL jednoduše popisuje, aby autoři nedělali kardinální prohřešky proti fyzice. Pokud budeme všechny koncepty aplikovat správně, budeme moci vysvětlit většinu věcí ve Star Treku.
V této části uvážíme, který koncept FTL cestování ve spojitosti s kterou provizí dovolí ve Star Treku provozovat každodenní FTL cestování bez tvoření neřešitelných paradoxů.
Nechť O´ je Enterprise. Místo vystřelování kulky může tedy sama Enterprise cestovat do *. Potom může (pomocí impulzního pohonu - podsvětelného) změnit svou vztažnou soustavu na stejnou, jako O. Potom může cestovat od * (resp. těsně po *) zpět k pozorovateli O, a dostat se k němu ještě před tím, než opustí svou pozici před prvním FTL letem (Enterprise tedy převezme také roli FTL signálu). Protože nebyla ani první, ani druhá FTL cesta zakázána, Enterprise by mohla používat každodenní hyperprostorový pohon jako způsob cestování zpět v čase.
Pokud by první provize měla fungovat, Enterprise by mohla být náhle přemístěna do paralelního vesmíru, aby se předešlo paradoxu (což by její posádku určitě nepotěšilo). Při platnosti druhé provize by si lodě disponující hyperprostorovým pohonem museli dávat pozor na to, ze které vztažné soustavy vstupují do hyperprostru (tedy, uskutečňují FTL cestu). Kvůli provizi se tedy mohou setkat se sami sebou před začátkem cesty (pokud by se tak stalo, „vesmír“ by musel loď z budoucnosti pravděpodobně zničit, aby nevznikl paradox). Obě tyto provize se tedy ke každodennímu používání FTL cestování ve Star Treku nehodí.
Jak je to s třetí provizí ? V ní již není možno používat hyperprostorový pohon jako „stroj času“, nicméně, je toho dosaženo zakazováním některých FTL cest kvůli jiným. Mohlo by se stát, že by Enterprise nemohla provést svou hyperprostrorovou cestu kvůli FTL signálu, který s ní ani cílem cesty přímo nesouvisí. To jsme také nikde ve Star Treku neviděli, což ukazuje na to, že tato provize by nebyla schopna odvrátit samo si odporující situace.
Zbývá nám tedy již jen čtvrtá provize. Ovšem díky neforemnosti češtiny se nám prozradila již na začátku. V angličtině se totiž způsob FTL cestování ve Star Treku označuje Warp, což samo o sobě nic nenaznačuje, ovšem protože se toto slovo nedá do češtiny nijak hezky přeložit, používá se hyperprostorové cestování, pojmenované po hyperprostoru (z ang. subspace - podprostor), tedy ekvivalentu toho, co jsme ve čtvrté provizi nazývali „speciální pole“. Přesto se pokusíme k témuž závěru dojít i složitější cestou.
Jak jsme si už řekli, v poslední provizi se pro FTL cestovatele používá speciální vztažná soustava. Lze si velmi jednoduše představit, že ono speciální pole, které má tuto vztažnou soustavu, je ve Star Treku hyperprostor (subspace), který je obsažen všude ve známém vesmíru. Hyperprostor bude tedy definovat pro každý bod prostoru jednotnou vztažnou soustavu. Pokud do hyperprostoru vstoupíte (tedy použijete hyperprostrorový pohon - warp), stane se tato vztažná soustava také vaší soustavou, bez ohledu na vaši relativní rychlost vzhledem k hyperprostoru. To umožní každodenní používání hyperprostorového pohonu bez nebezpečí vzniku neřešitelných paradoxů (jak bylo uvedeno v kapitole 6.5.4).
Častým problémem se stává to, že v různé literatuře se uvádí různé násobky rychlosti světla odpovídající téže hyperrychlosti. Pokud ovšem řekneme, že „rychlost Warp 3 odpovídá rychlosti 39c“, musíme také vzít v potaz, ve které vztažné soustavě je toto měřeno. Pro hyperprostor jako speciální vztažná soustava to znamená „39 násobek rychlosti světla ve vztažné soustavě hyperprostoru“.
Stejné poznámky je třeba uvést i tom, co se týče impulzního pohonu. V Technickém manuálu jsou uvedeny poměry učínnosti impulzních motorů u rychlostí nižších než 0,5c a speciální energetické úpravy pro rychlosti vyšší než 0,75c. Ale tyto rychlosti jsou relativistické - je třeba se zeptat, jaktože se při nich neprojevují žádné relativistické efekty. Odpověď můžeme najít opět v tomto manuálu : při impulzní rychlosti se používá hyperprostorové pole na „snížení hmotnosti lodi“ (takže ji lze jednodušeji pohánět). Lze se tedy shodnout na tom, že i tato rychlost je vztažná ke vztažné soustavě hyperprostoru. Zde si dovolím malou „historickou poznámku“. Po roce 2061 již konstanta rychlosti světla nebude c, ale C podle fyzika Zeframa Cochrana, který téhož roku poprvé předvedl nadsvětelný pohon na bázi hyperprostoru a dokázal existenci toho, čemu my říkáme čtvrtá provize.
Další zajímavou tematikou je rychlost Warp 10. „Funkce“ Warp nemá lineární průběh, ale spíše exponenciální. Rychlost Warp 9,9 je např. 3053-, ale rychlost Wapr 9,99 je již 7912-násobek rychlosti světla. Rychlost Warp 10 je považována za nekonečnou rychlost, tedy události opuštění startovního bodu a přílet do cílového bodu se odehrávají simultánně. Jak jsme si již řekli, otázka, zda jsou dvě události simultánní, závisí na vztažné soustavě. Rychlost Warp 10 lze tedy chápat jako nekonečná rychlost vzhledem ke vztažné soustavě hyperprostroru. Tuto rychlost pochopitelně nelze dosáhnout (bylo by k tomu potřeba nekonečně mnoho energie), ovšem je to naprosto jiný problém, než náš problém, jak překonat bariéru rychlosti světla. Ta je totiž přesně dána, zatímco z vývojem techniky ve Star Treku budou lodě postupně dosahovat např. rychlosti Warp 9,99; později třeba už Warp 9,999; po dalším vývoji třeba už Warp 9,99999 atd. Takže přestože se rychlost bude stále zvyšovat, rychlosti Warp 10 se nikdy nedosáhne, ale přesto budeme moci dosahovat stále vyšší rychlosti (tento aspekt lze přirovnat k množině přirozených čísel - pro každé přirozené číslo i existuje přirozené číslo i+1, ale čísla ¥ se přesto nikdy nedosáhne).
Díky této provizi vznikne nový standard měření času a délek. Čas a délka se budou moci měřit ve vztažné soustavě hyperprostru, bez ohledu na rychlost vůči němu. Lapidárně řečeno, aproximace Newtonovy relativity, které používáme v běžném životě budou v hyperprostoru platit při jakékoliv rychlosti.
Jak tedy vidíte, čtvrtá provize dokonale ukazuje funkčnost FTL cestování ve Star Treku.
Jak vidíte, čtvrtá provize padne Star Treku jako rukavička. Hyperprostorové cestování lze tedy shrnout takto : hyperprostor je pole, které definuje všem bodům známeho vesmíru tutéž vztažnou soustavu. Při používání hyperprostorového pohonu je cestovatelova vztažná soustava shodná se vztažnou soustavou hyperprostoru, bez ohledu na rychlost cestovatele. V této vztažné soustavě se tedy neprojevují relativistické efekty a proto neexistuje bariéra rychlosti světla. Hyperprostorové cestování navíc nelze použít k „návratu v čase“, ani k vytváření neřešitelných paradoxů.
(Celý tento koncept se velmi podobá Alcubierrově teorii FTL cestování [viz výše], až na to, že při FTL cestě si cestovatel ponechává takovou vztažnou soustavu, ve které byl původně, což může vytvořit neřešitelný paradox. Pokud se ovšem do jeho konceptu vpraví společná vztažná soustava pro všechny FTL cestovatele [obdoba hyperprostoru], tento problém se odstraní a celá teorie se bude podobat té, která existuje ve Star Treku.)
Hyperprostor lze ovšem použít i v lokálním měřítku. Ve vesmírných lodích se používá např. pro předávání informací jednotlivým systémům od senzorů (konkrétně rychlostí Warp 9,99; což je také rychlost přenosu hyperprostorových zpráv), aby bylo možno vyhodnocovat informace o lodích, které naši loď v hyperprostrou míjejí (opticky to pochopitelně nelze, protože světlo zde má stále rychlost c).
Ve Star Treku existují různé případy FTL cestování, které nemají přímou souvislost s hyperprostorem. Jedním z nich je např. černí díra, jejíž jeden konec se nachází poblíž planety Bajor v alfa kvadrantu a druhý v gama kvadrantu. Pokud by tento úkaz byl totožný s červí dírou, jak ji definuje Obecná teorie relativity, mohlo by její používání vyústit v neřešitelný paradox. Ve skutečnosti lze její „funkci“ objasnit tak, že se vlastně jedná o transhyperprostorový kanál (transwarp channel), který je součástí hyperprostoru, ale umožňuje dosáhnout lodím rychlostí vysoko nad Warp 9 bez použití jejich vlastního pohonu (resp. jen při použití impulsního pohonu).
Velmi dobrou otázkou je, jak se mohou ve Star Treku vyskytnout ojedinělé případy časových posunů do minulosti, aniž dojde k vzniku samo si odporující situace (tedy k paradoxu). Odpověď je velmi jednoduchá : ve Star Treku zřejmě neplatí jen čtvrtá provize, ale také provize druhá, „důsledková ochrana“, která se ovšem nevztahuje na FTL cestování (podle všeho lze překonat bariéru rychlosti světla jen hyperprostoru), ale na případné nebezpečí vzniku neřešitelných paradoxů. Naprosto dokonalý příklad funkce této provize lze nalézt v jedné epizodě série Star Trek : Voyager. Někteří členové posádky jsou na jisté planetě chyceni do jakési „trhliny v hyperprostoru“, která je přenese o den proti směru toku času. Ke konci epizody je ovšem vytvořena samo si odporující situace (posádka zabrání té události, která způsobila, že se dostali v čase tam, kde ji mohli zabránit). Tato řada události se tedy stane nemožná existence a také přestane existovat. Toto může být viděno jako výsledek této provize, protože ke konci epizody se začne odehrávat děj stejný jako na začátku, ale nedojde k objevení důsledku, který „začal“ onu řadu událostí vedoucí k samo si odporující situaci. Toto je tedy příklad toho, že pokud nějaká řada událostí hrozí k vyústění v neřešitelný paradox, „důsledková ochrana“ zajistí, aby se tato řada neuskutečnila.
V první části tohoto článku jsme se zaměřili na základní koncepty Speciální teorie relativity a zakončili jsme představením teorií FTL cestování a jejich aplikováním na Star Trek. Vyřešili jsme také problém neřešitelných paradoxů a shodli jsme se na tom, že pokud je FTL cestování v jakékoliv formě možné (doufejme že ano), potom je zabezpečeno pravděpodobně čtvrtou provizí a případné poruchy lineárního běhu času druhou provizí (nebo popřípadě první provizí).
Rád bych připomněl, že tato verze (verze září 1996) je pouze částečná. V příští verzi bude především doplněna o koncepty Obecné teorie relativity a pochopitelně stále rozšiřována na základě všech nových poznatků a informací, které se mi podaří získat. Doufejme také, že toto vše přispěje svou kapkou do mlýna, aby opravdu roku 2061 Zefram Cochrane (nebo někdo jiný) popsal skutečně fungující FTL koncept.
Především bych neobyčejně poděkoval [2], odkud jsem čerpal většinu informací, především příklady a diagramy. Stejný dík ovšem patří i všem ostatním autorům a jejich spisům. Díky, Alberte !
[1] Albert Einstein : K elektrodynamice pohybujících se částic
[2] Jason W. Hinson : Relativity and FTL travel (E-mail : hinson@bohr.physics.purdue.edu}
[3] Karel Bartuška : Deset kapitol ze speciální teorie relativity
[4] Václav Šindelář, Ladislav Smrž : Nová soustava jednotek SI
[5] Michael Okuda, Denise Okuda : Star Trek Chronology
[6] Michael Okuda, Rick Sternback : Star Trek Encyclopedia
[7] Star Trek Omnipedia
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1036
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved