| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Lineární optimalizační problém (bázické řešení, základní věta lineárního programování, způsoby převedení problému na kanonický tvar, prohibitivní ceny, lineární lomené programování)
Bázické řešení
Řešení soustavy A x = b se nazývá bázické, jestliže sloupce matice A, které odpovídají nenulovým složkám tohoto řešení, tvoří lineárně nezávislou soustavu vektorů.
Přípustné bázické řešení je takové bázické řešení, které navíc vyhovuje podmínkám nezápornosti x≥0.
Přípustné řešení úlohy LP je bázické právě tehdy, je-li krajním bodem množiny přípustných řešení.
Bázické řešení může mít nejvýše m nenulových složek, kde m = h(A). Je-li počet nenulových složek roven m, bázické řešení se nazývá nedegenerované. Bázické řešení s počtem nenulových složek menším než m se nazývá degenerované.
Přípustné řešení v problému lineárního programování:
x = [x1, x2, x3, . . . , xn]
Bazickým řešením nazýváme takové přípustné řešení, které získáme tak, že za (n-m) dosadíme 0, kde n – počet proměnných, m – počet omezení. Ostatní proměnné (těch m, které nemusí být rovní 0) nazveme bázické proměnné. Vektor x má tak nejvýše m nenulových složek, tj. tolik, kolik maximálně může v dané soustavě být lineárně nezávislých rovnic. Takových rovnic je tedy maximálně m. Počet bazických proměnných zůstává rovných m před i po transformacích.
Lineárním programováním (LP) se nazývá soubor matematických metod optimalizace, které prokázaly svoji efektivitu při řešení problémů přidělení zdrojů, zvláště těch, které se vyskytují v průmyslových výrobních systémech. Metody lineárního programování jsou algebraické metody založené na řadě rovnic a nerovnic, které stanoví omezení pro úlohu a jsou užívány pro optimalizaci matematického výrazu, který nazýváme cílovou funkcí. Cílová funkce a omezení naložená na problém musí být deterministické a musí být vyjádřeny v lineárním tvaru. Tato omezení omezují počet problému, které lze přímo řešit, ale od vzniku lineárního programování koncem čtyřicátých let došlo k velkému pokroku při použití metody na složitější úlohy.
Protože je lineární programování pravděpodobně nejčastěji používanou matematickou optimalizační metodou, existuje pro řešení úloh LP řada výpočetních programů. Metody LP jsou běžně používány např. pro řešení problémů směsí v naftových a chemických rafinériích, výběr dodavatelů nebo odběratelů pro velké podniky s mnoha závody, určení expedičních tras a časových plánů a správě a údržbě vozového parku.
Pro úlohu lineárního programování maximalizovat cTx na množině ![]() platí jedna
za tří možností:
platí jedna
za tří možností:

Kromě toho platí:
1. Je-li ![]() pak existuje základní přípustné
řešení,
pak existuje základní přípustné
řešení,
2. Je-li ![]() pak existuje základní optimální řešení.
pak existuje základní optimální řešení.
Jde o to se zbavit nerovností u omezujících rovnic. Pokud je nerovnost tak přidáme doplňkovou proměnou. Aby byl splněn kanonický tvar tak u zbývajících rovnice je třeba doplnit o pomocné proměnné.
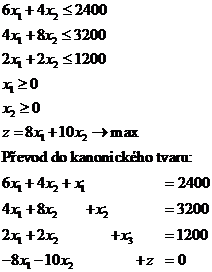
![]() - Doplňkové proměnné
- Doplňkové proměnné
![]() - Pomocné proměnné
- Pomocné proměnné

Pomocné proměnné, které byly zavedeny jako uměle
vytvořené bázické proměnné ![]() , jsme dosud
anulovali extremalizací uměle vytvořené kriteriální funkce. Existuje
však i jiný způsob anulování pomocných proměnných. Spočívá ve
využití tzv. prohibitivní ceny. Je to záporná cena −M, kde M je
vhodně zvolené velké kladné číslo. Simplexová metoda pracuje tak, že
pokud má problém přípustné řešení, pak pomocná proměnná, která
je v kriteriální funkci oceněná dostatečně velkou zápornou
cenou, nebude na konci výpočtu bázickou proměnnou. Jako nebázická
proměnná je pak anulována automaticky.
, jsme dosud
anulovali extremalizací uměle vytvořené kriteriální funkce. Existuje
však i jiný způsob anulování pomocných proměnných. Spočívá ve
využití tzv. prohibitivní ceny. Je to záporná cena −M, kde M je
vhodně zvolené velké kladné číslo. Simplexová metoda pracuje tak, že
pokud má problém přípustné řešení, pak pomocná proměnná, která
je v kriteriální funkci oceněná dostatečně velkou zápornou
cenou, nebude na konci výpočtu bázickou proměnnou. Jako nebázická
proměnná je pak anulována automaticky.
Lineární lomené Programování (maximalizace haléřového ukazatele)
xj – množství j-tého výrobku
cj – odbytová cena j-tého výrobku
dj – nákladny na j-tý výrobek

výsledkem je hodnota hrubé produkce
Omezující podmínky

j – řádek
i – sloupec
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1299
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved