| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Analytická geometrie
Příklad1: GEM řešte homogenní SLR :

Řešení
![]() =
=
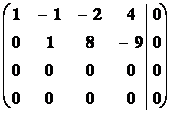 Þh(A) = h(
Þh(A) = h(![]() ) = 2 < n
) = 2 < n
Þ soustava má nekonečně mnoho řešení, která jsou závislá na volbě (n h) parametrů. V tomto případě 4 2 = 2, čili 2 parametry.
Položíme x4 = s, x3 = r Þ x2 = 8r+9s a x1 = 6r+5s.
To je  kde r,sIR.
kde r,sIR.
Je zřejmé, že každé řešení ![]() homogenní soustavy je LK vektorů
homogenní soustavy je LK vektorů ![]() a
a ![]() neboli
neboli ![]() I
I![]() (tj.
(tj. ![]() je prvkem lineárního obalu těchto vektorů).
je prvkem lineárního obalu těchto vektorů).
Věta: Obecné řešení homogenní SLR je vektorový prostor dimenze n h , kde n je počet neznámých a h je hod(A).
Příklad2: GEM řešte SLR :
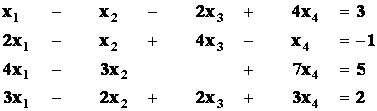
Řešení
![]() =
=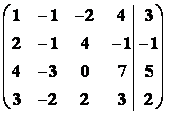
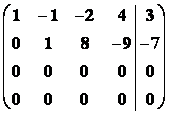 Þh(A) = h(
Þh(A) = h(![]() ) = 2 < n
) = 2 < n
Þ soustava má nekonečně mnoho řešení, která jsou závislá na volbě 2 parametrů. Položíme x4 = s, x3 = r Þ x2 = 8r+9s a x1 = 6r+5s.
To je 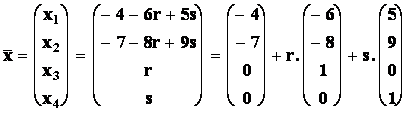 kde r,sIR.
kde r,sIR.
Porovnáním tohoto výsledku s výsledkem
předchozího příkladu zjistíme, že v obecném
řešení soustavy je navíc vektor ![]() .
Tento vektor představuje partikulární
řešení soustavy (tj. jedno konkrétně
zvolené řešení soustavy, např.
.
Tento vektor představuje partikulární
řešení soustavy (tj. jedno konkrétně
zvolené řešení soustavy, např. ![]() ).
).
Věta: Nechť SLR je řešitelná (tj. h(A) = h(![]() ).
Potom platí :
).
Potom platí :
OŘ = libovolné PŘ + OŘ homogenní soustavy
S využitím SLR lze řešit geometrické úlohy. V analytické geometrii se po zavedení soustavy souřadnic nahrazují geometrické pojmy algebraickými s cílem řešit geometrické úlohy algebraickou cestou (výpočtem).
Označme ![]() (n-krát) množinu všech uspořádaných n‑tic reálných čísel. Prvky této
množiny budeme nazývat body, množině
(n-krát) množinu všech uspořádaných n‑tic reálných čísel. Prvky této
množiny budeme nazývat body, množině ![]() budeme říkat euklidovský prostor dimenze n.
Body budeme značit velkými písmeny a zapisovat je v hranatých závorkách.
Např.
budeme říkat euklidovský prostor dimenze n.
Body budeme značit velkými písmeny a zapisovat je v hranatých závorkách.
Např.
A = ![]()
je bod n-rozměrného euklidovského prostoru ![]() .
Reálným číslům
.
Reálným číslům ![]() budeme říkat souřadnice bodu A.
Uspořádané n‑tice reálných čísel
mají tedy dva významy. Chápeme je jednak jako aritmetické vektory z
budeme říkat souřadnice bodu A.
Uspořádané n‑tice reálných čísel
mají tedy dva významy. Chápeme je jednak jako aritmetické vektory z ![]() (nadále je budeme zapisovat v kulatých
závorkách, např.
(nadále je budeme zapisovat v kulatých
závorkách, např. ![]() =
= ![]() )
, a jednak jako body z
)
, a jednak jako body z ![]() .
.
Vztah mezi nimi definujeme :
Definice: Nechť P = ![]() je bod z
je bod z ![]() a
a ![]() =
= ![]() je vektor z
je vektor z ![]() .
Zobrazení, které přiřazuje každému bodu PI
.
Zobrazení, které přiřazuje každému bodu PI![]() a každému vektoru
a každému vektoru ![]() I
I![]() bod XI
bod XI![]() o souřadnicích
o souřadnicích
![]() (i = 1,,n)
(i = 1,,n)
se nazývá bodově-vektorová relace.
Jiný zápis je
X = P + ![]()
a můžeme si relaci představit jako posunutí bodu
P do bodu X o vektor ![]() .
.
Příklad: Bodu
![]() z
z ![]() a vektoru
a vektoru ![]() =
= ![]() z
z ![]() odpovídá podle bodově-vektorové relace
bod
odpovídá podle bodově-vektorové relace
bod ![]() z
z ![]() .
.
Dále v ![]() definujeme
definujeme
Skalární součin vektorů ![]() a
a
![]() je číslo
je číslo
![]() .
.![]() =
=![]()
Velikost vektoru ![]() Þ
Þ ![]()
Příklad1:
Vypočtěte velikost vektoru ![]() z
z ![]() .
.
Řešení ![]()
Příklad2:
Určete vzdálenost bodů A =![]() a B =
a B =![]() z
z ![]() .
.
Řešení Vzdálenost bodů A, B je délka vektoru ![]() =
= ![]() ,
,
vzd(A,B) =
![]() =
=![]() =
=![]() .
.
Pro úhel
j dvou nenulových vektorů ![]() ,
,![]() platí cos j =
platí cos j =
Příklad:
Určete úhel vektorů ![]() a
a ![]() z
z ![]() .
.
Řešení
cos j = =
= =
=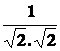 =
=![]() Þ j =
Þ j = ![]() =
60°.
=
60°.
Poznámka1 j = ![]() (vektory jsou kolmé) Þ skalární součin se rovná nule.
(vektory jsou kolmé) Þ skalární součin se rovná nule.
Poznámka2:
Dva vektory ![]() ,
,![]() se nazývají kolineární
(rovnoběžné s jednou přímkou), jestliže platí:
se nazývají kolineární
(rovnoběžné s jednou přímkou), jestliže platí: ![]() =k.
=k.![]() ,
kde kIR.
,
kde kIR.
Poznámka3:
Tři vektory ![]() ,
,![]() ,
,![]() se nazývají komplanární
(rovnoběžné s jednou rovinou), jestliže aspoň jeden z nich je LK ostatních dvou.
se nazývají komplanární
(rovnoběžné s jednou rovinou), jestliže aspoň jeden z nich je LK ostatních dvou.
Definice: Nechť je dán bod P = ![]() z
z ![]() a h
lineárně nezávislých vektorů
a h
lineárně nezávislých vektorů ![]() ,
,![]() ,…,
,…,
![]() z
z ![]() .
Množina bodů X z
.
Množina bodů X z ![]() které vyhovují rovnici:
které vyhovují rovnici:
X = P + t1 ![]() + t2
+ t2 ![]() …+ th
…+ th ![]()
kde ti I R, se nazývá lineární
podprostor dimenze h vnořený do ![]() .
.
Poznámka: Bod
P se nazývá počátek
lineárního podprostoru ( LP ), reálným číslům ti říkáme parametry, LN vektory ![]() ,
,![]() ,…,
,…,
![]() jsou
směrové
vektory LP. Lineární obal vektorů
jsou
směrové
vektory LP. Lineární obal vektorů ![]() ,
,![]() ,…,
,…,
![]() ,
tj.
,
tj. ![]() tvoří vektorový prostor, kterému říkáme zaměření LP.
tvoří vektorový prostor, kterému říkáme zaměření LP.
Říkáme bodově-vektorová rovnice LP a můžeme ji také zapsat
X = P + ![]()
Přímka
LP dimenze 1 vnořený do ![]() se nazývá přímka v
se nazývá přímka v ![]() .
Přímka p daná počátkem P =
.
Přímka p daná počátkem P = ![]() a směrovým vektorem
a směrovým vektorem ![]() =
= ![]() je tedy množina bodů X, pro které
platí :
je tedy množina bodů X, pro které
platí :
p:
X = P + t![]() tIR,
tIR,
Rozepsáním této bodově-vektorové rovnice pomocí souřadnic dostaneme parametrické rovnice přímky p :
![]()
![]()
![]()
Lineární obal <![]() > = t
> = t![]() je zaměřením přímky p.
je zaměřením přímky p.
Příklad: Máme
rozhodnout, zda bod Q =![]() leží na přímce p dané počátkem P =
leží na přímce p dané počátkem P = ![]() a směrovým vektorem
a směrovým vektorem ![]() =
= ![]() .
.
Řešení: Přímka má bodově-vektorovou rovnici
p:
X = ![]() + t
+ t![]() tIR,
tIR,
Bod Q leží na přímce, jestliže tIR takové, že
![]()
![]()
![]()
Řešení této soustavy je ![]() .
Bod Q proto leží na přímce.
.
Bod Q proto leží na přímce.
Poznámka: Pro
![]() = B A (přímka určená body A, B) dostaneme
= B A (přímka určená body A, B) dostaneme
X = A + t (B A) tIR,
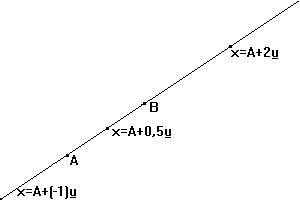
Pokud tI< > je to rovnice úsečky AB .
Vzájemná poloha dvou přímek
Uvažujme v ![]() přímky p, q
přímky p, q
p: X1 = P + r ![]()
q: X2 = Q + s ![]()
a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů r, s, které dosazeny do uvedených rovnic určí bod X1 = X2. Pro r, s dostáváme rovnici
r ![]() s
s![]() = Q P
= Q P
Rozepíšeme ji po složkách a dostaneme
ra1 sb1 = q1 p1
ran sbn = qn pn
soustavu n rovnic o neznámých r, s. Pro přímky p, q pak nastane jedna z možností:
Soustava má ![]() řešení
a vektory
řešení
a vektory ![]() ,
,
![]() jsou LZ (h(A) = h(
jsou LZ (h(A) = h(![]() ) = 1).
Přímky p, q jsou totožné.
) = 1).
Přímky p, q jsou totožné.
Soustava nemá žádné řešení a vektory ![]() ,
,
![]() jsou LZ (h(A) = 1, h(
jsou LZ (h(A) = 1, h(![]() ) = 2).
Přímky p, q jsou rovnoběžné.
) = 2).
Přímky p, q jsou rovnoběžné.
Soustava má právě jedno řešení a vektory ![]() ,
,
![]() jsou LN (h(A) = h(
jsou LN (h(A) = h(![]() ) = 2).
Přímky p, q jsou různoběžné.
) = 2).
Přímky p, q jsou různoběžné.
Soustava nemá žádné řešení a vektory ![]() ,
,
![]() jsou LN (h(A) = 2, h(
jsou LN (h(A) = 2, h(![]() ) = 3).
Přímky p, q jsou mimoběžné.
(jenom pro n >
) = 3).
Přímky p, q jsou mimoběžné.
(jenom pro n >
Příklad:
Rozhodněte o vzájemné poloze přímek v ![]() .
.
p: X1 = P + r![]()
q: X2 = Q + s![]()
jestliže
a)
P = ![]() ,
,
![]() =
= ![]() ,
Q =
,
Q = ![]() ,
, ![]() =
= ![]()
b)
P = ![]() ,
, ![]() =
= ![]() ,
Q =
,
Q = ![]() ,
, ![]() =
= ![]() .
.
Řešení
a)
Protože ![]() = 3
= 3![]() ,
jsou vektory
,
jsou vektory ![]() ,
,![]() lineárně závislé. Přímky p, q jsou tedy rovnoběžné, musíme však
zjistit, zda totožné nebo různé. Soustava rovnic má tvar
lineárně závislé. Přímky p, q jsou tedy rovnoběžné, musíme však
zjistit, zda totožné nebo různé. Soustava rovnic má tvar
3r + 9s = 10
r + 3s = 2
r 3s =

 Þ h(A) ¹ h(
Þ h(A) ¹ h(![]() )
)
Soustava nemá řešení a tedy přímky p, q jsou rovnoběžné.
b)
Vektory ![]() ,
,![]() jsou lineárně nezávislé. Přímky p, q jsou různoběžky nebo
mimoběžky. Nyní budeme řešit soustavu rovnic
jsou lineárně nezávislé. Přímky p, q jsou různoběžky nebo
mimoběžky. Nyní budeme řešit soustavu rovnic
3r s =
2r 2s =
r 3s =
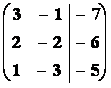

 Þh(A) = h(
Þh(A) = h(![]() ) = 2 = n
) = 2 = n
Soustava má jediné řešení s = 1, r = 2. Existuje tedy jediný průsečík přímek p, q, bod
R = Q + s ![]() = P + r
= P + r ![]() =
= ![]() .
Přímky p, q jsou různoběžné.
.
Přímky p, q jsou různoběžné.
Rovina
LP dimenze 2 vnořený do ![]() se nazývá rovina v
se nazývá rovina v ![]() .
Rovina r daná počátkem P =
.
Rovina r daná počátkem P = ![]() a směrovými vektory
a směrovými vektory ![]() =
= ![]() a
a ![]() =
= ![]() je tedy množina bodů X, pro které platí :
je tedy množina bodů X, pro které platí :
r
X = P + t![]() + u
+ u![]() t,uIR,
t,uIR,
Rozepsáním této bodově-vektorové rovnice pomocí souřadnic dostaneme parametrické rovnice roviny r
![]()
![]()
![]()
![]()
Lineární obal <![]() ,
,![]() > = t
> = t![]() + u
+ u![]() je zaměřením roviny r
je zaměřením roviny r
Příklad:
Určete parametrické rovnice roviny r,
procházející body A = ![]() ,
B =
,
B = ![]() a C =
a C = ![]() .
.
Řešení : Jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme r

Volbou ![]() = B A =
= B A = ![]() ,
,
![]() = C A =
= C A = ![]() sestrojíme její směrové vektory (jsou LN) a dostaneme bodově‑vektorovou
rovnici roviny
sestrojíme její směrové vektory (jsou LN) a dostaneme bodově‑vektorovou
rovnici roviny
r X = A + r![]() + s
+ s![]() =
= ![]() + r
+ r
![]() + s
+ s
![]()
a dále parametrické rovnice
x = 1 2s
y = 1 + r + 2s
z = 1 s
Nadrovina
LP dimenze n 1 vnořený do ![]() se nazývá nadrovina v
se nazývá nadrovina v ![]() .
.
Poznámka: V
trojrozměrném prostoru (![]() ) je nadrovinou právě rovina, v rovině (
) je nadrovinou právě rovina, v rovině (![]() )
je nadrovinou přímka, atd.
)
je nadrovinou přímka, atd.
Vzájemná poloha lineárních podprostorů
Nechť lineární podprostor rh má zaměření Vh a dimenzi h, podprostor rk má zaměření Vk a dimenzi k, a nechť h ³ k . Potom :
Podprostory rk a rh jsou rovnoběžné, jestliže Vk Ì Vh . Pokud rk rh ¹ Æ jsou rovnoběžné incidentní , jinak rovnoběžné neincidentní ( rk rh Æ
Podprostory rk a rh jsou různoběžné, nejsou-li rovnoběžné a jejich průnik není prázdný tj. rk rh ¹ Æ
Podprostory rk a rh jsou mimoběžné, nejsou-li rovnoběžné a jejich průnik je prázdný tj. rk rh Æ
Praktický výpočet
Uvažujme v ![]() lineární podprostory:
lineární podprostory:
![]() X = P +
t1
X = P +
t1![]() + t2
+ t2![]() …+ th
…+ th![]() ,
,
![]() Y = Q +
u1
Y = Q +
u1![]() + u2
+ u2![]() …+ uk
…+ uk![]() ,
,
kde dimenze h ³ k a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů, které dosazeny do uvedených rovnic určí body X = Y. Dostáváme rovnici
t1![]() …+ th
…+ th![]() u1
u1![]() uk
uk![]() = Q P
= Q P
Rozepíšeme ji po složkách a dostaneme soustavu n
rovnic o (h + k) neznámých. Početně určíme vzájemnou polohu tak, že řešíme ![]() .
.
Je‑li hod(A) = h, pak Vk Ì Vh
a tedy podprostory jsou rovnoběžné. Pokud h(A) = h(![]() ) ,
tj. pokud rk rh ¹ Æ jsou rovnoběžné incidentní, jinak jsou rovnoběžné neincidentní.
) ,
tj. pokud rk rh ¹ Æ jsou rovnoběžné incidentní, jinak jsou rovnoběžné neincidentní.
Je‑li hod(A) > h a h(A) = h(![]() ) jsou
různoběžné, jinak mimoběžné.
) jsou
různoběžné, jinak mimoběžné.
Příklad:
Určete vzájemnou polohu rovin a a r v ![]() , jsou‑li :
, jsou‑li :
a ![]()
r ![]() .
.
Řešení: Hledejme společné body obou rovin. Přitom dimenze h = k = 2. Položíme sobě rovny pravé strany obou rovnic. Rozepsáním do souřadnic získáme soustavu čtyř rovnic o 4 neznámých. Její rozšířená matice soustavy je

 Þ h(A) = 4 > h
Þ h(A) = 4 > h
(nejsou rovnoběžné) a zároveň h(A) = h(![]() ) = 4 = n
(soustava má právě jedno řešení) s2 =
2, s1 = 1, t2 =
1, t1 = 3.
) = 4 = n
(soustava má právě jedno řešení) s2 =
2, s1 = 1, t2 =
1, t1 = 3.
Dosazením do rovnice kterékoliv z rovin a r vypočteme společný průsečík obou rovin tj. a r , např. pro r
Q =![]() =
= ![]()
Zkoumané roviny jsou tedy různoběžné a jejich společným průnikem je bod Q
Množině všech řešení určité SLR můžeme dát geometrický
význam. Množina je buď Æ, nebo
je lineárním podprostorem vnořeným do prostoru ![]() .
Jeho dimenzí je počet volitelných neznámých v dané soustavě rovnic, tj. n h.
.
Jeho dimenzí je počet volitelných neznámých v dané soustavě rovnic, tj. n h.
Příklad: Řešte SLR :
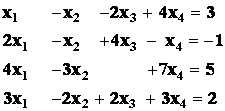
Řešení
![]() =
=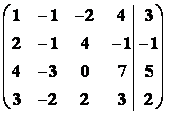
 Þh(A) = h(
Þh(A) = h(![]() ) = 2 < n
) = 2 < n
Interpretujeme‑li řešení jako bod z ![]() ,
pak
,
pak
![]()
Zápis odpovídá rovnici lineárního podprostoru
dimenze 2 vnořeného do ![]() .
Množinu všech řešení dané soustavy lze tedy interpretovat jako rovinu vnořenou do prostoru E4
.
.
Množinu všech řešení dané soustavy lze tedy interpretovat jako rovinu vnořenou do prostoru E4
.
Poznámka: Soustava lineárních rovnic, jejímž řešením je LP dimenze n h vnořený do prostoru ![]() ,
se nazývá obecný
zápis tohoto podprostoru.
,
se nazývá obecný
zápis tohoto podprostoru.
Příklad: Obecný zápis LP
![]()
je tedy SLR
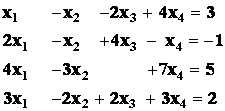
Je zřejmé, že jedna lineární rovnice o n neznámých
![]() = b
= b
definuje LP dimenze n 1 vnořený do ![]() ,
protože
,
protože ![]() =
=![]() = 1.
Tato rovnice je obecná rovnice nadroviny v
= 1.
Tato rovnice je obecná rovnice nadroviny v ![]() .
Koeficienty
.
Koeficienty ![]() určují normálový vektor
určují normálový vektor ![]() =
=![]() ,
tj. vektor, který je kolmý k nadrovině (tj. kolmý ke všem směrovým
vektorům LP).
,
tj. vektor, který je kolmý k nadrovině (tj. kolmý ke všem směrovým
vektorům LP).
Např. rovnice ![]()
je obecná rovnice přímky v rovině (![]() )
a její normálový vektor je
)
a její normálový vektor je ![]() =
=![]() .
.
Příklad1:
Určete obecný zápis roviny ![]() v
v ![]() ,
známe‑li její parametrické vyjádření
,
známe‑li její parametrické vyjádření

Řešení : Hledané rovnice dostaneme vyloučením parametrů r, s.
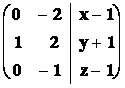
 Þ řešení bude
Þ řešení bude ![]()
Jedná se zřejmě o nadrovinu v ![]() ,
protože se dá vyjádřit jedinou rovnicí.
,
protože se dá vyjádřit jedinou rovnicí.
Příklad2:
Určete parametrické rovnice přímky p v ![]() , která má obecný zápis:
, která má obecný zápis: ![]() ,
, ![]() .
.
Řešení : Bod X hledaného průniku musí vyhovovat oběma rovnicím a je tedy řešením soustavy dvou rovnic o třech neznámých.

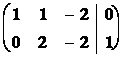 Þ h(A) = h(
Þ h(A) = h(![]() ) = 2 <
) = 2 <
Þ ![]() ,
,
![]() ,
z = t, závisí na jednom parametru t I R a je parametrickým vyjádřením přímky p.
,
z = t, závisí na jednom parametru t I R a je parametrickým vyjádřením přímky p.
Příklad3:
Rozhodněte o vzájemné poloze přímky p a roviny r v ![]() .
.
![]()
![]()
Řešení : Rovnici přímky rozepíšeme po složkách do parametrických rovnic
x = 3 t
y = 1 4t
z = 3 + 3t
Dosadíme x, y, z do rovnice roviny, tj. hledáme takové t, aby platilo
t) + 2 (1 4t) + 3 (3 + 3t) + 4 = 0
Po úpravě dostaneme 18 = 0. Rovnice nemá řešení, neexistuje společný bod, přímka p je rovnoběžná s rovinou r
Vzdálenost bodu M od podprostoru
X = P + t1 ![]() + t2
+ t2 ![]() …+ th
…+ th ![]()
kde ti I R, je velikost vektoru ![]() = X M , pro který platí:
= X M , pro který platí:
![]() .
. ![]() = 0
= 0
pro i = 1,..,h, tj. ![]() je kolmý na všechny vektory ze zaměření LP.
je kolmý na všechny vektory ze zaměření LP.
Příklad: V ![]() určete vzdálenost bodu M =
určete vzdálenost bodu M = ![]() od roviny
od roviny ![]() ,
kde P =
,
kde P = ![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() .
.
Řešení: Vektor ![]() = X M =
= X M = ![]() .
Podmínky kolmosti tohoto vektoru k vektorům
.
Podmínky kolmosti tohoto vektoru k vektorům ![]() ,
,
![]() jsou ve tvaru :
jsou ve tvaru :
![]() .
. ![]() = 0,
= 0, ![]() .
.
![]() = 0,
= 0,
tj.
![]() .
. ![]() = 0
= 0
![]() .
. ![]() = 0
= 0
a určují soustavu rovnic pro t , u :
5t + 2u =
t + u =
Řešení soustavy t = 1, u = Þ ![]() =
=
![]() Þ
hledaná vzdálenost bodu M od dané
roviny je
Þ
hledaná vzdálenost bodu M od dané
roviny je ![]() =
=![]() .
.
Poznámka: Vzdálenost bodu
B = ![]() od nadroviny
od nadroviny
![]() = b je daná vztahem :
= b je daná vztahem :

Þ Rovina z předchozího příkladu
je nadrovinou v ![]() .
Bylo by proto možné určit její obecnou rovnici
.
Bylo by proto možné určit její obecnou rovnici
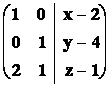
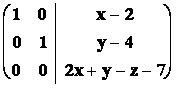 Þ
Þ ![]()
a počítat podle vzorce
d =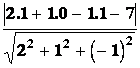 =
=![]() =
=![]()
Vzdálenost dvou podprostorů
![]() X = P + t1
X = P + t1![]() + t2
+ t2![]() …+ th
…+ th![]() ,
,
![]() Y = Q + u1
Y = Q + u1![]() + u2
+ u2![]() …+ uk
…+ uk![]() ,
,
je velikost vektoru ![]() =
= ![]()
![]() ,
kde
,
kde ![]() I
I ![]() ,
,
![]() I
I![]() , pro který platí:
, pro který platí:
![]() .
. ![]() = 0, i = 1,,h
= 0, i = 1,,h
![]() .
. ![]() = 0, j = 1,,k.
= 0, j = 1,,k.
Příklad: V ![]() určete vzdálenost dvou mimoběžek:
určete vzdálenost dvou mimoběžek:
p: x = 7 + 3t q: x = 21 + 6r
y = 4 + 4t y = 4r
z = 2t z = 2 r
Řešení: Vzdálenost je velikost vektoru
![]() =
= ![]()
![]() =
= ![]()
kde ![]() I p,
I p, ![]() Iq, který je kolmý k oběma směrovým vektorům přímek, tj.
Iq, který je kolmý k oběma směrovým vektorům přímek, tj.
![]() .
. ![]() = 0,
= 0, ![]() .
. ![]() = 0,
= 0,
Provedeme součiny
![]() .
. ![]() = 0
= 0
![]() .
. ![]() = 0
= 0
a dostaneme soustavu
![]()
![]()
Řešení soustavy je t = 2, r = Þ ![]() =
=
![]()
hledaná vzdálenost je ![]() =
=![]() =
=![]() = 13
.
= 13
.
Přepíšeme‑li rovnici přímky určené dvěma body A,B
X = A + t.(B A) tIR,
na tvar
X = (1 t).A + t.B tIR,
potom při označení l t, l = t lze psát
X = l A + l B
Mluvíme o lineární kombinaci bodů A, B. Čísla l l mohou být libovolná, musí však pro ně platit
l l
Pokud tI< > je to rovnice úsečky AB , tj. platí
l ³ l ³
Potom mluvíme o konvexní lineární kombinaci bodů A, B.
Tj. každý bod X úsečky AB lze psát ve tvaru:
X = l A + l B
l l
l ³ l ³
Jsou‑li A, B, C tři body neležící v jedné přímce, potom každý bod XIDABC lze psát ve tvaru:
X = l A + l B + l C
l l l
l ³ l ³ l ³
Důkaz: Každý bod X trojúhelníka ABC lze psát ve tvaru
X = l A + b U , kde l b l ³ b ³
kde U je bod na úsečce CB Þ můžeme jej zapsat U = j C + j B, kde j j = 1 , j ³ j ³ 0 (jinak, U je konvexní LK bodů C, B). Dosazením dostaneme
X = l A + b j C + j B ) = l A + b j C + b j B
kde l b j j l ³ b ³ j ³ j ³
Položíme‑li b j l b j l , je
l l l = 1, kde l ³ l ³ l ³ 0, cbd.
Podmnožina v ![]() se nazývá konvexní, když s každými body A, B obsahuje i
každý bod úsečky AB.
se nazývá konvexní, když s každými body A, B obsahuje i
každý bod úsečky AB.
Tak např. úsečka, trojúhelník, kruh jsou konvexní, avšak mezikruží není. Konvexní množina je také I kvadrant v rovině xy.
Analogicky jako u trojúhelníka lze dokázat, že konvexní polyedr (mnohostěn) o vrcholech A1, A2,, Ap lze vyjádřit rovnicí
X =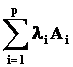
s vedlejšími podmínkami
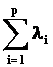 = 1
= 1
li ³ 0 , (i = 1,2,,p).
Konvexní polyedr je vlastně jakýsi konvexní lineární obal bodů A1, A2,, Ap, je to totiž nejmenší konvexní množina, která všechny dané body obsahuje.
Příklad:
Trojúhelník ABC je dán vrcholy : A = ![]() ,
B =
,
B = ![]() ,
C =
,
C = ![]() .
Vyjádřete souřadnice libovolného bodu trojúhelníka pomocí konvexní lineární
kombinace jeho vrcholů. Ověřte, zda body P =
.
Vyjádřete souřadnice libovolného bodu trojúhelníka pomocí konvexní lineární
kombinace jeho vrcholů. Ověřte, zda body P = ![]() a Q =
a Q = ![]() leží v trojúhelníku ABC.
leží v trojúhelníku ABC.
Řešení: Pro XIABC platí:
X = l A + l B + l C
l l l
l ³ l ³ l ³
Označíme‑li X = ![]() a dosadíme-li za A, B, C dostaneme
a dosadíme-li za A, B, C dostaneme
![]() l
l ![]() +
l
+
l ![]() +
l
+
l ![]()
a po rozepsání do složek
x = l l l
y = l l
Nejprve řešíme pro bod P = ![]() :
:
4 = l l l
4 = l l
Ke dvěma rovnicím můžeme připojit třetí rovnici
1 = l l l
Rozšířená matice soustavy vypadá
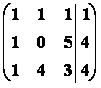
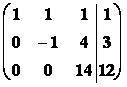 Þ l =
Þ l = ![]() , l =
, l = ![]() , l =
, l = ![]()
Jak vidíme, není splněná podmínka l ³ Þ bod PÏABC.
Pro bod Q = ![]() : 2 = l l l
: 2 = l l l
3 = l l
1 = l l l
Rozšířená matice soustavy vypadá

 Þ l =
Þ l = ![]() , l = 0, l =
, l = 0, l = ![]()
Jsou splněné podmínky l ³ l ³ l ³ 0 Þ bod QIABC.
Obecná rovnice nadroviny v En je
![]()
nebo
![]()
V prostoru E2 je nadrovinou přímka a
víme , že každá přímka v rovině nám rozdělí tuto rovinu na dvě poloroviny. V
prostoru E3 je nadrovinou vlastně rovina a každá rovina rozdělí
prostor na dva tzv. poloprostory. Analogicky si můžeme představit, že každá
nadrovina v prostoru ![]() nám opět rozdělí celý prostor En na dva poloprostory. Lze dokázat, že jestliže
do této rovnice dosadíme souřadnice bodu X, který v nadrovině neleží, rovnice
nebude splněná a znaménko čísla b závisí na tom, ve kterém ze dvou poloprostorů
určených nadrovinou leží bod X. Čili pro body jednoho z poloprostoru bude
platit
nám opět rozdělí celý prostor En na dva poloprostory. Lze dokázat, že jestliže
do této rovnice dosadíme souřadnice bodu X, který v nadrovině neleží, rovnice
nebude splněná a znaménko čísla b závisí na tom, ve kterém ze dvou poloprostorů
určených nadrovinou leží bod X. Čili pro body jednoho z poloprostoru bude
platit
![]()
pro body druhého poloprostoru bude platit
![]()
Příklad:
Přímka o rovnici ![]() je nadrovina v
je nadrovina v ![]() .
Tato přímka rozděluje
.
Tato přímka rozděluje ![]() na dva poloprostory (v tomto případě mluvíme o
polorovinách) dané podmínkami
na dva poloprostory (v tomto případě mluvíme o
polorovinách) dané podmínkami ![]() ,
,
![]() .
.
Poznámka: Množinu všech řešení určité soustavy lineárních nerovnic můžeme geometricky interpretovat jako průnik poloprostorů. Protože každý z poloprostorů je konvexní množinou, průnikem vznikne také konvexní množina, která má navíc konečný počet vrcholů. Lze dokázat, že pokud tato množina je omezená, pak je konvexním polyedrem. Tyto poznatky patří k teoretickému základu pro rozpracování teorie lineárního programování.
Příklad s ekonomickou tématikou: Závod může vyrobit nejvíce 60 kusů výrobků V1 a nejvíce 20 kusů výrobků V2 , přitom počet kusů výrobků V1 musí být nejméně čtyřnásobkem počtu kusů výrobků V2 . Napište tyto ekonomické podmínky ve tvaru lineárních vztahů.
Řešení: Označme x1 počet kusů výrobků V1 a x2 počet kusů výrobků V2 . Pak podmínky v úloze lze vyjádřit takto :
![]() ,
, ![]() ,
, ![]() .
.
Navíc z ekonomické interpretace proměnných x1, x2 vyplývá jejich nezápornost, tj.
![]() ,
, ![]() .
.
Geometricky každá z uvedených pěti podmínek
představuje polorovinu a jejich průnik je trojúhelník. Tento trojúhelník je
konvexním polyedrem s vrcholy ![]() ,
,
![]() ,
,
![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1101
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved