| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Než vyslovíme definici derivace funkce, proveďme tyto úvahy z geometrie :
Mějme dánu křivku o rovnici ![]() a na ní bod
a na ní bod ![]() .
Zvolme její další její bod
.
Zvolme její další její bod ![]() ,
,
![]() .
Spojíme oba body přímkou; nazveme ji sečnou křivky.
.
Spojíme oba body přímkou; nazveme ji sečnou křivky.
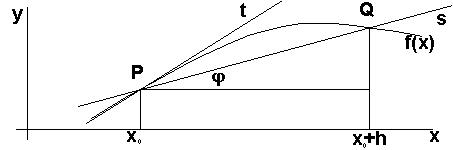
Její směrnici vyjádříme  .
Budeme‑li zmenšovat absolutní hodnotu h,
bude se bod Q posunovat po křivce
směrem k bodu P. Poloha sečny se bude
měnit, sečna se bude otáčet kolem bodu P.
V případě, že
.
Budeme‑li zmenšovat absolutní hodnotu h,
bude se bod Q posunovat po křivce
směrem k bodu P. Poloha sečny se bude
měnit, sečna se bude otáčet kolem bodu P.
V případě, že ![]() ,
přechází tato sečna v tečnu křivky. Její směrnice bude vyjádřena
jako limitní případ směrnice sečny
,
přechází tato sečna v tečnu křivky. Její směrnice bude vyjádřena
jako limitní případ směrnice sečny
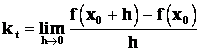
Definice: Existuje‑li pro funkci f : y = f(x) a číslo x0 limita
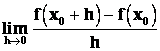
nazýváme ji derivací
funkce f(x) v bodě x0. Značíme ji ![]() ,
tedy
,
tedy
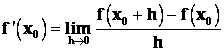
Vyjádřeno slovy : Derivace funkce v bodě x0 je limita podílu přírůstku funkce f v bodě x0 a přírůstku argumentu x, jestliže se přírůstek argumentu blíží k nule.
Číslu h v definici derivace říkáme přírůstek nezávisle proměnné x (argumentu x); h může být kladné i záporné. Místo h užíváme také označení D x („delta x“). Označíme‑li x1 = x0 + h Þ h = x1 ‑ x0 , lze uvedený vzorec pro derivaci napsat také ve formě

Rozdíl funkčních hodnot f(x0 + h) ‑ f(x0), resp. f(x1) ‑ f(x0) nazýváme přírůstek funkce v bodě x0. Lze jej též označit D f(x0) nebo D y0. Pak lze psát
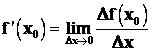
často bude psát místo x0 jen x
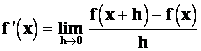
v tomto výrazu bude x pevné, h
proměnné. Bude‑li tato limita existovat pro všechny hodnoty x daného intervalu I, bude ![]() funkcí proměnné x I I a nazveme ji derivací funkce v intervalu I.
funkcí proměnné x I I a nazveme ji derivací funkce v intervalu I.
Pro označení derivace funkce y = f(x) užíváme symbolů
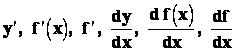
a chceme‑li vyznačit hodnotu derivace v bodě x0, mohou být použity symboly
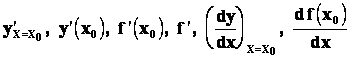
Existují‑li limity
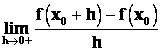 resp.
resp. 
nazýváme je derivace zprava resp. derivace zleva.( jednostranné derivace)
Jsou‑li uvažované limity nevlastní, nazýváme je derivacemi nevlastními.
Věta: Má‑li f(x) v bodě x0 derivaci, pak je v bodě x0 spojitá.
Důkaz : Předpokládejme existenci derivace v bodě x0.
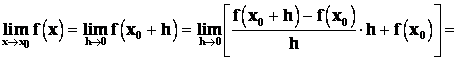
![]() je spojitá v bodě x0.
je spojitá v bodě x0.
Poznámka1: Větu o
vztahu mezi spojitostí a derivací nelze obrátit. Spojitost funkce v x0
nezaručuje existenci derivace v tomto bodě, jak ukazuje příklad : ![]() je v bodě 0 spojitá, nemá však v tomto bodě derivaci, neboť
je v bodě 0 spojitá, nemá však v tomto bodě derivaci, neboť
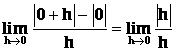 neexistuje, protože
neexistuje, protože
 a
a ![]() .
.
Poznámka2: Předpoklad existence vlastní derivace ve větě o vztahu mezi spojitostí a derivací je podstatný. Má‑li funkce v bodě nevlastní derivaci, nemusí být v tomto bodě spojitá. Např. funkce y = sign(x).
![]() a
a ![]() .
.
Čili derivace v bodě nula existuje a je nevlastní (+¥), ale víme, že funkce je v bodě nula nespojitá.
Příklad1: Vypočtěte (podle definice) derivaci funkce y = C (konstanta).
Řešení : Definice derivace

funkční hodnoty ![]() .
.
Dosadíme do vzorce ![]() .
.
Příklad2:
Vypočtěte derivaci funkce ![]() a stanovte její hodnotu v bodech x1 = 2, x2 = ‑3,
x3 = 0.
a stanovte její hodnotu v bodech x1 = 2, x2 = ‑3,
x3 = 0.
Řešení : funkční hodnoty
![]()
![]() .
.
Dosadíme : 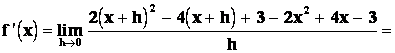
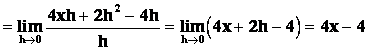 .
.
![]()
![]() ;
; ![]() .
.
Pravidla pro derivování.
Nechť funkce f(x) a g(x)
mají pro x I J
derivaci ![]() a
a ![]() .
Potom platí :
.
Potom platí :
![]()
![]()
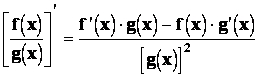 , pro g(x) ¹
, pro g(x) ¹
![]()
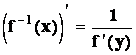 kde
kde ![]()
Důkaz :
2. ![]() =
=![]() =
=
=![]() =
=![]() =
=![]() .
.
![]() =
=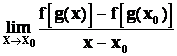 =
=
 =
=
=
 =
=![]()
Derivace základních elementárních funkcí
![]() pro
xIR,
pro
xIR,
![]() pro
xIR,
pro
xIR,
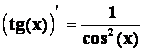 pro
x ¹ (2k+1)
pro
x ¹ (2k+1)![]() ,
k celé,
,
k celé,
 pro
x ¹ kp, k celé,
pro
x ¹ kp, k celé,
![]() pro
xIR,
pro
xIR,
![]() pro
xIR,
pro
xIR,
![]() pro
x >
pro
x >
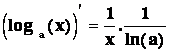 pro
x >
pro
x >
![]() pro
xID(f), nIR,
pro
xID(f), nIR,
 pro xI
pro xI
 pro xI
pro xI
![]() pro
xIR,
pro
xIR,
![]() pro xIR,
pro xIR,
Některé důkazy:
![]()
![]()
![]()
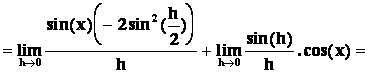
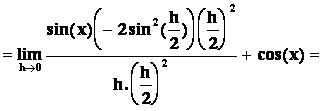
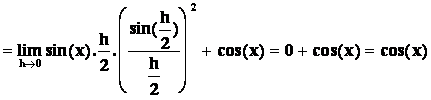
9) ![]()


12)![]() (položíme‑li y = arctg(x) je x = tg(y))
(položíme‑li y = arctg(x) je x = tg(y))
podle věty o derivaci inverzní funkce je

Příklad1:
Vypočtěte derivaci funkce ![]() .
.
Řešení : 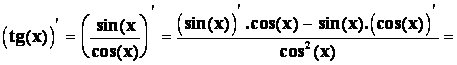
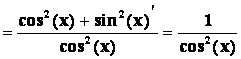
Příklad2:
Vypočtěte derivaci funkce ![]() .
.
Řešení : Máme složenou funkci f(x) = h(g(x)), kde
y = g(x) = ![]() je vnitřní funkce a její derivace
je vnitřní funkce a její derivace ![]() ,
,
h(g(x)) = h(y) = y5 je funkce vnější a její derivace ![]() .
.
Z věty o derivaci složené funkce plyne:
![]()
Příklad3:
Vypočtěte derivaci funkce ![]() .
.
Řešení : analogicky: y = g(x) = sin(x), h(y) = y6 Þ
![]()
Příklad4:
Vypočtěte derivaci funkce ![]() pro x >
pro x >
Řešení : 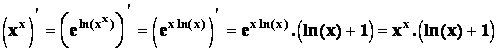
Rovnice tečny a normály
Derivace funkce f(x) v bodě x0
v geometrickém významu značí směrnici tečny ke křivce bodě x0.
Lze tedy určit rovnici tečny a normály (normála je kolmice k tečně
v bodě dotyku) : Je‑li dána funkce f a na ní dotykový bod tečny
T = ![]() ,
vypočteme její směrnici Kt =
,
vypočteme její směrnici Kt =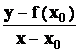 = f ¢(x0) . Podmínka pro směrnice přímek vzájemně kolmých
v rovině je že jejich součin je roven ‑1, proto směrnice normály
je Kn =
= f ¢(x0) . Podmínka pro směrnice přímek vzájemně kolmých
v rovině je že jejich součin je roven ‑1, proto směrnice normály
je Kn =  pro f ¢(x0) ¹
pro f ¢(x0) ¹
Rovnice tečny ![]()
Rovnice normály 
Je‑li f ¢(x0) = 0,
Rovnice tečny : y = f(x0) Rovnice normály: x = x0
Příklad:
Určete rovnici tečny a normály ke křivce dané rovnicí ![]() v bodě
v bodě ![]() .
.
Řešení : Bod dotyku má druhou souřadnici f(x0) = 4( 3
Þ ![]()
![]() Þ Kt = f ¢(-1) = -4, Kn =
Þ Kt = f ¢(-1) = -4, Kn = 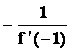 =
=![]()
Þ Rovnice tečny
: ![]() Þ
Þ ![]() ,
,
Rovnice normály ![]() Þ
Þ ![]() .
.
Diferenciál funkce
Říkáme, že funkce f je diferencovatelná v bodě x0 , existuje‑li konečná derivace v tomto bodě, tj. f ¢(x0) = A IR.
V tomto případě můžeme přírůstek funkce Dy = f(x) f(x0) aproximovat přírůstkem k tečně v bodě x0 tj. hodnotou f ¢(x0).(x x0). Nazveme jej diferenciálem funkce v bodě x0 . Označíme :
dy = f ¢(x0).(x x0) = f ¢(x0).Dx resp.
d f(x0) = f ¢(x0).Dx
Protože pro funkci y = x platí dy = dx = Dx lze diferenciál psát ve formě
d f(x0) = f ¢(x0)dx
Píšeme‑li místo x0 jenom x, pak diferenciál funkce f v bodě x označujeme
dy = d f(x) = f ¢(x)dx
Z odvozeného
diferenciálu dy = f ¢(x)dx
lze určit ![]() , tj. symbol dříve zavedený pro derivaci,
který nyní můžeme považovat za zlomek.
, tj. symbol dříve zavedený pro derivaci,
který nyní můžeme považovat za zlomek.
Užití diferenciálu funkce
Při malých hodnotách Dx platí Df(x) df(x) , tj. přibližnou hodnotu
funkce v bodě x0 + Dx můžeme
vyjádřit ![]() .
.
Příklad:
Vypočtěte přibližnou hodnotu ![]() .
.
Řešení : Je třeba dosadit
do funkce f(x) = ![]() .
.
Pro x0 = 16
je f(x0) =![]() =
2 , dx = x x0 = 15.8
=
2 , dx = x x0 = 15.8
f ¢(x) =![]() =
= 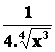 Þ f ¢(x0) =
Þ f ¢(x0) =  =
=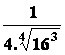 =
=![]()
Platí ![]() = f(x0) + f ¢(x0)dx
= f(x0) + f ¢(x0)dx
Þ ![]() 2 +
2 + ![]() (
(
Derivace vyšších řádů
Má‑li funkce f v každém bodě intervalu (a,b) derivaci f ¢(x), pak tato derivace je také funkcí xI(a,b). Bude‑li funkce f ¢ mít v bodě x0I(a,b) derivaci, říkáme, že funkce f má v tomto bodě druhou derivaci, nebo derivaci druhého řádu. Značíme ji nejčastěji
f ¢¢(x0) , y¢¢(x0) , ![]()
Obecně n‑tou derivací funkce f rozumíme první derivaci (n 1) derivace. Značíme ji
![]() ,
, ![]() ,
, ![]() .
.
Příklad:
Vypočtěte ![]() funkce
funkce ![]() .
.
Řešení ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Věty o střední hodnotě diferenciálního počtu
Rolleova věta: Je‑li funkce f spojitá v uzavřeném intervalu <a,b> a má derivaci na otevřeném intervalu (a,b), přičemž f(a) = f(b), potom existuje aspoň jedno číslo b I(a,b) takové, že f ¢ b
Rolleova věta zaručuje existenci alespoň jednoho bodu C, ve kterém je derivace funkce f rovna nule ale neříká nic o tom , jak tento bod najít. Těchto bodů může existovat více.
Geometrické znázornění Rolleovy věty :

Lagrangeova věta: (věta o střední hodnotě )
Je‑li
funkce f spojitá v uzavřeném
intervalu <a,b> a má derivaci na otevřeném intervalu (a,b), potom existuje aspoň
jedno číslo b I(a,b)
takové, že ![]()
Geometrický význam této věty říká, že existuje alespoň jeden bod v (a,b), v němž tečna ke křivce je rovnoběžná se spojnicí koncových bodů A, B.
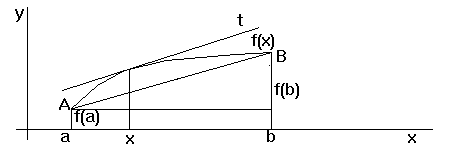
Cauchyova věta: (zobecněná věta o střední hodnotě )
Nechť platí:
funkce f a g jsou spojité v uzavřeném intervalu <a,b>
pro každé xI(a,b) existuje f ¢(x) a g ¢(x),
g ¢(x) ¹ 0 pro xI(a,b).
Potom existuje cI(a,b) tak, že platí:
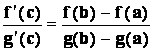 .
.
Věta: (o významu první derivace pro průběh funkce)
Nechť je funkce f spojitá v intervalu I a nechť v každém vnitřním bodě tohoto intervalu existuje derivace f ¢(x). Je‑li:
f ¢(x) > Þ f(x) je rostoucí v intervalu I,
f ¢(x) < Þ f(x) je klesající v intervalu I,
f ¢(x) = 0 Þ f(x) je konstantní v intervalu I,
Důkaz: Buďte a, b I I, a < b, Aplikujeme‑li větu o střední hodnotě na interval <a,b>, dostaneme
![]()
![]() , kde b I(a,b).
, kde b I(a,b).
Je‑li f ¢(x) > Þ f ¢ b > Þ f(a) f(b) > 0 (funkce je rostoucí).
Ověření tvrzení 2) a 3) je zcela analogické.
Příklad:
Rozhodněte o intervalech monotónnosti funkce ![]() .
.
Řešení : O monotónnosti funkce rozhodne znaménko její první derivace
![]()
Změny znaménka první derivace mohou nastat pouze v bodech, kde f ¢(x) = 0 (stacionární body), tj. x1 = 0, x2 = 1. Pro
xI ¥,0) znaménko f ¢(x) je ( f ¢(x) > Þ f(x) je rostoucí,
xI(0,1) znaménko f ¢(x) je (+).( f ¢(x) < Þ f(x) je klesající,
xI ¥) znaménko f ¢(x) je (+).(+) f ¢(x) > Þ f(x) je rostoucí.
L´Hospitalovo pravidlo
Nechť funkce
f a g mají derivaci v určitém okolí bodu b (x ¹ b) a nechť ![]()
![]() = 0.
Pak
= 0.
Pak

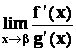
jestliže limita na pravě straně existuje.
L´Hospitalovo pravidlo platí, jedná‑li se o
výpočet limity „neurčitého výrazu“ typu (![]() )
nebo (
)
nebo (![]() ) . Jsou ale další neurčité výrazy, které se dají převést na tyto typy, např. (0 ¥ ¥ ¥) , (
) . Jsou ale další neurčité výrazy, které se dají převést na tyto typy, např. (0 ¥ ¥ ¥) , (![]() ),(
),(![]() )
a (
)
a (![]() ).
).
Příklad1:
Stanovte ![]() .
.
Řešení : Výraz typu (![]() ).
Použijeme L´H.
).
Použijeme L´H.
![]() =
=![]() =
=![]() =
=![]() .
.
Příklad2:
Stanovte ![]() .
.
Řešení : Výraz typu (![]() ).
Použijeme L´H.
).
Použijeme L´H.
![]() =
=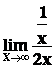 =
=![]() =0.
=0.
Příklad3:
Stanovte  .
.
Řešení : Výraz typu (¥ ¥). Upravíme na typ (![]() )
a použijeme L´H.
)
a použijeme L´H.
 =
= =
=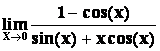 =
=
=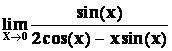 =0.
=0.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 925
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved