| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
OTÁZKY DO TESTU ANKC
1. Transformační zákon vektoru, transformační matice.
používá se při transformaci souřadnic z jedné do druhé souřadné soustavy (např. z lokálních do globálních).

[Kg] = [T]T * [Kl] * [T]
kde T je transformační matice
a úhel Alfa je kladný po směru
hodinových ručiček
2. Transformační zákon tenzoru II. řádu.
[A] je tenzor

3. Interpretace tenzoru II. řádu.
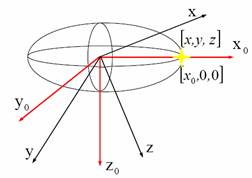 Každý tenzor se dá geometricky interpretovat pomocí centrální kvadriky.
Je-li tenzor symetrický, centrální kvadrika je elipsoid.
Každý tenzor se dá geometricky interpretovat pomocí centrální kvadriky.
Je-li tenzor symetrický, centrální kvadrika je elipsoid.
4. Müllerův-Breslaův princip.
U staticky neurčité konstrukce s neposuvnými podporami zhotovené z lineárně pružného
materiálu, která není ovlivněna proměnou teplotou, získáme př činkovou čáru reakce nebo
vnitřní síly tak, že uvolníme vazbu v místě hledané veličiny a v daném místě aplikujeme
zatížení odpovídající působení hledané veličiny. Pokud zatížení má takovou hodnotu, že
výsledná deformace ve směru a orientaci hledané veličiny je minus jedna, potom průhybová
křivka kopíruje př činkovou čarou hledané reakce či vnitřní síly.
5. Deformační varianta řešení úloh MTP, Bernoulli-Navierova hypoteza.
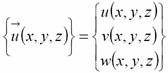 Hledáme tři neznámé funkce vektoru pole posunutí
Hledáme tři neznámé funkce vektoru pole posunutí
Pomocí geometrických rovnic vypočteme v bodě tenzor malých deformací [Aε]. Na základě fyzikálních rovnic dopočteme v tom samém bodě tenzor napětí [Aσ]. Dále máme k dispozici tři podmínky rovnováhy – Cauchyho rovnice. Získáme soustavu tří parciálních diferenciálních
rovnic Laméových pro výše uvedené složky pole posunutí. Soustavu parciálních diferenciálních rovnic je třeba doplnit statickými a geometrickými okrajovými podmínkami.
B-N hypotéza: Průřezy rovinné a kolmé k ose prutu před deformací, zůstávají rovinné a kolmé k ose prutu i po deformaci.
- díky ní se def. varianta řešení úloh MTP zjednodušuje z hledání tří neznámých funkcí tří
nezávislých proměnných na hledání tří neznámých funkcí, ale pouze jedné nezávislé proměnné
6. Lagrangeův princip virtuálních posunutí.
![]()
virtuální práce vnitřních sil se rovná virtuální práci sil vnějších
7. Tvarové, aproximační funkce.

Lineární aproximace osových posunů u(x):
kubická aproximace průhybů w: 
kde hi jsou bázové fce
8. Vektor transformovaného zatížení.
![]()
kde Γ budeme rozuět integrál přes objem V tělesa, Ω přes povrch, neboli zatíženou plochu tělesa
9. Matice tuhosti.
matice tuhosti jsou vlastně styčníkové podmínky rovnováhy, kde základními neznámými jsou styčníkové posuny (u, w) a pootočení (φ), je různá pro různě uložené pruty (V-V, V-K, K-V) a je vždy symetrická podle hlavní diagonály
10. Předpoklady Kirrchhoffovy teorie desek
deska – jeden rozměr(z) má mnohem menší než zbylé dva -> rovinná kce (x,y) zatížená kolmo ke střednicové rovině
Předpokládáme, že ve střednicové rovině (x,y) nedochází k posunutím ve směru souřadnicových os x,y, k popisu řešení tedy stačí jedna neznámá – průhyb w
dále se zavádí předpoklad, že normála ke střednicové rovině zůstane normálou k průhybové ploše
11. Silová varianta řešení MTP.
řeší se za pomoci Airyho funkce a hledáme tři neznáme složky tenzoru rovinné napjatosti
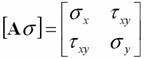
k dispozici jsou dvě Cauchyho podmínky rovnováhy.
dále platí 3 podmínky kompatibility (v rovině je jedna)
12. Stěnová rovnice, Airyho funkce.
zavádíme Airyho funkci F(xy), která popisuje rovinnou napjatost a je se složkami tenzoru napětí identitami
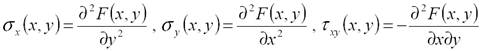
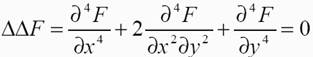
a stěnová rovnice pak vypadá:
13. Hlavní napjatost.
je jí dosaženo tehdy, pokud najdeme takové natočení souřadných os (do hlavních směrů), že vymizí všechna smyková napětí a tenzor napjatosti je tvořen pouze hlavními normálovými napětími σx, σy a σz -> extrémní hodnoty normálového napětí.
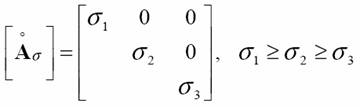
14. Deviátor napětí.
dají se z něj vypočítat I2S a I3S, dále zavedeme dva odvozené invarianty J a υ a z nich pak hlavní napětí σi
![]()
kde
15. Hustota potenciální energie deformace změny tvaru.
Při zatěžování dochází u lineárně pružného materiálu ke kumulaci hustoty potenciální energie deformace. Část se kumuluje do objemové změny a část do změny tvaru. Například při tahové zkoušce oceli je hustota potenciální energie, která působí na změnu tvaru 6,5 krát. větší než hustota potenciální energie, která působí na změnu objemu.
16. Co jsou invarianty?
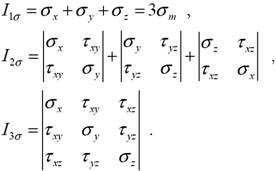 jsou to determinanty tenzoru napjatosti, které jsou nezávislé na
natočení souřadného systému, vždy mají stejnou hodnotu – jsou
invariantní
jsou to determinanty tenzoru napjatosti, které jsou nezávislé na
natočení souřadného systému, vždy mají stejnou hodnotu – jsou
invariantní
(neproměnné)
17. Předpoklady teorie II. řádu.
- lze linearizovat geometrické vztahy mezi deformacemi a posuny (geometricky lineární
výpočet)
- rozložení osových sil se při deformaci konstrukce nemění
- rovnováha se vyjadřuje na deformovaném tvaru
18. Co je to kritické břemeno, kritické zatížení?
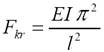 pokud se zatížení silou F blíží kritickému Eulerovu břemeni, roste
průhyb i moment nade
pokud se zatížení silou F blíží kritickému Eulerovu břemeni, roste
průhyb i moment nade
všechny meze – dochází ke ztrátě stability, Eulerovo kritické břemeno:
19. Co je to vzpěrná délka a kdy má smysl s ní počítat?
je to vzdálenost dvou inflexních bodů ohybové čáry používá se u stabilitního výpočtu štíhlých tlačených prutů, umožňuje odhadnout charakter geometrických imperfekcí, které jsou pro uvažovanou konstrukci nebezpečné
20. Přibližný vztah mezi přetvořením dle teorie I. řádu a II. řádu.
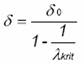 λkrit je součinitel kritického zatížení
λkrit je součinitel kritického zatížení
δ0 jsou spočtené imperfekce dle teorie I. řádu
δ jsou imperfekce dle teorie II. řádu
21. Co je to imperfekce?
jsou to nějaké odlišnosti od ideálu(modelu pro teorii I. řádu) - neexistuje žádný ideální prut (homogenní, prizmatický, přímý). například počáteční zakřivení prutu
22. Představte vnitřní sílu bimoment.

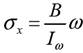
![]()
zavádí se pomocí identity a dále platí, že
ve dvou rovnoběžných rovinách proti sobě působí 2 momenty na nějakém rameni
23. Co získáte derivací bimomentu podle x ?
moment od ohybového kroucení 2Mx
![]() 24. Co platí pro hlavní výsečovou
pořadnici?
24. Co platí pro hlavní výsečovou
pořadnici?
výsečový statický moment i oba výsečové deviační momenty se rovnají 0
25. Jaké znáte výsečové charakteristiky průřezu.
![]()
výsečový statický moment:
![]() výsečové deviační momenty:
výsečové deviační momenty:
26. Představte základní myšlenku výpočtu smykového napětí vlivem
vázaného kroucení.
smykové napětí vlivem vázaného kroucení se spočítá jako součet smykových napětí od volného kroucení (1Mx) + od ohybového kroucení (2Mx) -> τxs = 1τxs + 2τxs
27. Co je to deformační zóna?
zóna, ve které se projevuje deformace od zatížení, za hranicí deformační zóny se deformace od zatížení neprojevuje, rozumné hloubky: (1,5 až 5) * šířka základu
28. Jak funguje Winkler-Pasternakovo podloží.
řeší poddajné podloží konstantní tloušťky na nestlačitelném podkladu, tuhost podloží charakterizují parametry (konstanty) c1(tuhost pružiny ve směru její osy) a c2(smyková vazba mezi sousedními pružinami c1), vrstva se vodorovně nedeformuje, neznámou je pouze sedání w
29. Který z parametrů W-P podloží s hloubkou deformační zóny roste a který
klesá.
c1 klesá a c2 roste
30. Jaký je vztah mezi řešením pružné vrstvy a W-P podloží?
W-P podloží se jeví jako trochu tužší než pružná vrstva, neboť ta dovoluje vodorovné posuny
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1319
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved