Planimetrie a stereometrie

2b - úloha 1

Zobrazte řez krychle ABCDEFGH rovinou , jsou‑li body P, Q, R dány takto:

2b - úloha 2

Zobrazte řez krychle ABCDEFGH rovinou , jsou‑li body K, L, M dány takto:

2b - úloha 3

Zobrazte kvádr ABCDA´B´C´D´, pro který platí:

Zobrazte řez kvádru rovinou r, která je rovnoběžná s přímkou a prochází body D´a M, kde M je střed úsečky

8b - úloha 1

Na vrcholu kopce stojí rozhledna vysoká 30 m.Patu rozhledny vidíme po úhlem a 28° 30´; vrchol rozhledny vidíme pod úhlem b

Jak vysoko je vrchol kopce nad horizontální rovinou pozorovacího místa?

8b - úloha 2

Letadlo letí ve výšce h = 2200 m k pozorovatelně P. V okamžiku prvního měření bylo místo P z letadla vidět pod výškovým úhlem a = 23°, při druhém měření pod úhlem b = 58°. Vypočítejte vzdálenost, kterou letadlo uletělo mezi oběma měřeními

10a - úloha 1

V pravidelném čtyřbokém jehlanu ABCDV je dáno ; .

Určete:

a)  odchylku roviny r podstavy od roviny s boční stěny

b)  odchylku boční hrany CV od roviny r

10a - úloha 2

V pravidelném čtyřbokém jehlanu ABCDV je dáno ; .

Určete:

a)  odchylku obou sousedních bočních stran

b)  vzdálenost vrcholu A od přímky .

10a - úloha 3

Je dán kvádr ABCDEFGH o rozměrech: ; ; 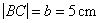. Bod K je středem hrany AD.

a)  Sestrojte skutečnou velikost D BHK.

15b - úloha 1

Sestrojte všechny lichoběžníky ABCD, které mají a ,  = 4 cm,  = 5 cm a jejich úhlopříčky svírají úhel e

15b - úloha 2

Sestrojte všechny trojúhelníky ABC, je‑li dáno: t_b = 6; t_c I R⁺; g . Proveďte diskusi.

15b - úloha 3

Jsou dány dvě různoběžky a, b a bod A I a. Sestrojte všechny kružnice, které se dotýkají přímky b a současně přímky a v bodě A.

16b - úloha 1

U pravidelného čtyřbokého jehlanu se rovnají délky jeho podstavných i bočních hran. Vypočítejte jeho povrch, je‑li dán jeho objem V.

16b - úloha 2

Objem pravidelného šestibokého hranolu je 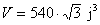. Podstavná hrana a a výška v jsou v poměru a : v = 3 : 5. Vypočítejte a, v a povrch S.

19b - úloha 1

Řešte trojúhelník, jsou‑li dány délky jeho stran: a = 8,5 cm; b = 6,3 cm; c = 9,2 cm

19b - úloha 2

Řešte trojúhelník, je‑li dáno: c = 59 cm; a 30´; S = 1087 cm²

19b - úloha 3

V lichoběžníku ABCD je dáno a = 30 cm; b = 13 cm; c = 16 cm; d = 15 cm. Určete velikosti vnitřních úhlů a obsah lichoběžníku.

25a - úloha 1

Do koule o průměru 2r rovnostranný válec a rovnostranný kužel. Určete poměr povrchů a objemů těchto těles.

25a - úloha 2

Nádoba tvaru duté polokoule je naplněna vodou do výšky v = 10 cm. Kolik litrů vody obsahuje, je‑li vnitřní průměr nádoby d = 28 cm? Úlohy na aplikaci

26a - úloha 1

Sestrojte úsečku velikosti užitím…

a)  Pythagorovy věty

b)  Euklidovy věty o odvěsně

c)  Euklidovy věty o výšce

26a - úloha 2

Vypočítejte délku tětivy v kružnici o poloměru r = 17 cm, víte‑li, že tato tětiva rozděluje průměr k ní kolmý v poměru 1 : 16.

28b - úloha 1

Sestrojte D ABC, je‑li dáno: t_a = 3 cm; c = 5 cm; g

28b - úloha 2

Jsou dány dvě protínající se kružnice. Jedním jejich průsečíkem veďte takovou přímku, která vytíná na obou kružnicích shodné tětivy.

28b - úloha 3

Jsou dány soustředné kružnice k₁, k₂, k₃ s poloměry r₁ > r₂ > r₃ a bod A I k₃. Sestrojte rovnostranný D ABC tak, aby jeho vrcholy B, C ležely na k₁, k₂.

29b - úloha 1

Jsou dány dvě různoběžky a, b a bod M, který leží uvnitř jednoho jejich úhlu. Sestrojte všechny kružnice, které procházejí bodem M a dotýkají se daných přímek a, b.

29b - úloha 2

Zkonstruujte trojúhelník ABC, je‑li dáno:
a : b = 4 : 3;  g = 45°;  t_c = 9 cm