| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
P(A B) = P(A) + P(B) - P(A B)
P(A B) = P(A / B) . P(B) = P(B/A) . P(A)
![]()
![]()
![]()
![]()
![]()
![]()
Binomické rozdělení
![]() , k = 0, 1, …, n
, k = 0, 1, …, n
E(X) = np
D(X) = np(1– p)
Poissonovo rozdělení
p n (n p np = l = konst . . . parametr
![]() E(X) = l D(X) = l
E(X) = l D(X) = l
Hypergeometrické rozdělení
P(X=m) = 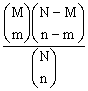 , m = max(0, M–N +
n), . . ., min(M, n)
, m = max(0, M–N +
n), . . ., min(M, n)
= 0 jinak
E(X) = n![]() D(X)
=
D(X)
= ![]()
Normální rozdělení
![]()
Φ(-u) = 1 – Φ(u)
Statistická indukce
![]()
Dvoustranný interval spolehlivosti pro parametr m
P( I ![]() a
a
a) s je znám ![]()
b) s není znám ![]()
Jednostranné intervaly spolehlivosti pro parametr
( ![]() levostranný,
levostranný,
( ![]() pravostranný,
pravostranný,
a) s je
znám ![]() ,
,
b) s není znám ![]()
a) s
známe, pak 
b) s neznáme, pak 
Dvoustranný interval spolehlivosti pro s

Dvoustranný interval spolehlivosti pro s

Dvoustranný interval spolehlivosti pro p pI![]()
![]()
Jednovýběrový t-test při
známém s ![]()
|
Alternativa A |
Kritický obor K |
|
m m m >m m < m |
u > ua u > u2a u < – u2a |
Jednovýběrový t-test při neznámém s
|
Nulová hypotéza H0 |
Alternativa A |
Testové kritérium |
Kritický obor K |
|
m m |
m m m >m m < m |
|
t > ta ( n–1) t > t2a ( n–1) t < – t2a ( n–1) |
|
Nulová hypotéza H0 |
Alternativa A |
Testové kritérium |
Kritický obor K |
|
|
|
|
F > Fa /2 ( m–1; n–1) F > Fa (m–1; n–1) |
Testy hypotéz pro
testování významnosti rozdílu dvou výběrových průměru při
neznámých rozptylech ![]() =
=![]() s
s
|
Nulová hypotéza H0 |
Alternativa A |
Testové kritérium |
Kritický obor K |
|
m m |
m m m >m m < m |
|
t > ta (m + n–2) t > t2a (m + n–2) t < – t2a (m + n–2) |
s2
= ![]()
Test hypotéz
při testování významnosti rozdílu dvou výběrových průměru
při neznámých rozptylech ![]()
![]() :
:
|
Nulová hypotéza H0 |
Alternativa A |
Testové kritérium |
Kritický obor K |
|
m m |
m m m >m m < m |
|
t > ta x t > t2a x t < – t2a x |
ta x 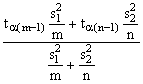
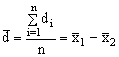

|
Kritický obor K |
|
t > ta ( n–1) t > t2a ( n–1) t < – t2a ( n–1) |
Test hypotézy o parametru p alternativního rozdělení v případě velkých výběrů
a) jednovýběrový ![]()
b) dvouvýběrový
u =
![]()
![]() ,
, ![]()
Cochranův
test: ![]()
Schéma uspořádání výsledků výpočtu analýzy rozptylu jednoduchého třídění se stejným počtem n opakování v třídách.
|
Zdroje variability |
Součet čtverců odchylek hodnot |
Stupně volnosti f |
Rozptyl |
F-test |
|
Mezi průměry tříd |
|
f1 = m – 1 |
|
|
|
Uvnitř tříd (reziduální) |
|
fr = m(n – 1) |
|
Fa(f1, fr) |
|
Celková |
S= S1+Sr |
f = mn – 1 |
S -
(Scheffé-ho) metoda: ![]()
T -
(Tukey-ho) metoda T: ![]()
c - test dobré shody: ![]()
Vypočtené testové kritérium budeme porovnávat s tabulkovou hodnotou c - rozdělení pro f = (k–c–1)
Dixonův test: ![]() pro x1 nebo
pro x1 nebo ![]() pro xn,
pro xn,
Qa n (tabulková hodnota pro Dixonův test, hladinu významnosti a a n rozsah souboru)
Kolmogorov - Smirnovův
test: ![]()
Vypočtené testové kritérium budeme porovnávat s tabulkovou hodnotou Da(n)
Tabulka
kritických hodnot Da je sestavena pouze pro n 40. Pro
výběry větších rozsahů s
musí kritické hodnoty určit podle vztahů (pro a =
![]() a
a ![]()
Wilcoxon - Whiteův test: T= min (T1, T2).
T1 a T2 jsou součty pořadových čísel pro jednotlivé původní soubory.
Vypočtené testové kritérium budeme porovnávat s tabulkovou hodnotou Ta m n
Při velkých rozsazích souborů je testovým kritériem náhodná veličina uT
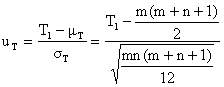
uT porovnáváme s kritickou hodnotu normovaného normálního rozdělení ua
Dvouvýběrový Wilcoxonův test:
Za testové kritérium U je považována menší hodnota z U1, U2, kdy
![]() a
a ![]()
T1 a T2 jsou součty pořadových čísel pro jednotlivé původní soubory. U porovnáváme s Ua m n
Wilcoxonův test: W = min(W1, W2)
W1 = součet pořadových čísel pro diference záporné (-)
W2 = součet pořadových čísel pro diference kladné (+)
Porovnáme s kritickou hodnotu Wa(n)
Znaménkový test. Při použití testu je testovým kritériem Z pouze menší počet z „+ a - znamének“ u diferencí di mezi párovými hodnotami znaku. Pokud Z < Za n, přijímá se alternativní hypotéza (pro n - počet znamének a hladinu významnosti a
Kruskal - Wallisův test: ![]()
KW porovnáváme s c a k–1
Neményiho metoda podrobnějšího vyhodnocení: Je-li diference Ti - Tj větší nebo rovna kritické hodnotě Da pro Neményiho metodu, zamítá se hypotéza o neprůkaznosti diference (tabulkové hodnoty se hledají pro hladinu významnosti a, pro k počet porovnávaných tříd a N opakování v každé třídě).
Kontingenční tabulky
asociace
|
a |
b |
|
c |
d |
test závislosti
![]() >
>![]()
síla závislosti
V=![]()
Q=![]()
Y=
průběh závislosti
b=![]()
a=![]()
kontingence
test závislosti
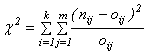 >
>![]()
síla závislosti

![]()

 , t = min (r, s)
, t = min (r, s)
Regresní a korelační analýza
Jednoduchá regrese a korelace
![]() a
a ![]()
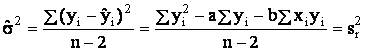 reziduální
rozptyl
reziduální
rozptyl
soustava normálních rovnic an + bSxi = Syi
aSxi + bSxi2 = Sxi yi
sdružené
regresní přímky ![]()
![]()
výběrová kovariance ![]()
![]()
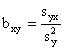
měření
těsnosti závislosti ![]() ,
, ![]() ,
, ![]() ,
, ![]()
test významnosti regresního
koeficientu ![]() , kde
, kde ![]()
K = pro f = n–2
test
významnosti koeficientu korelace ![]() K =
pro f = n–2
K =
pro f = n–2
Intervalový odhad pro hodnotu regresního koeficientu b
P(b1 < b < b2) = 1– a pro b1, 2 = b ta f sb
Intervalový odhad pro hodnotu koeficientu korelace r
Převedeme
hodnotu r na hodnotu z (veličiny Z,
která vykazuje přibližně normální rozdělení hodnot). ![]() (jsou
k dispozici převodní tabulky)
(jsou
k dispozici převodní tabulky)
Stanovíme hranice intervalu spolehlivosti z1, z2 pro hodnotu z veličiny Z podle vzorce:
P(z1
< Z < z2) = 1– a pro z1,
2 = z 
Převedeme hranice z1, z2 na hodnoty r1, r2 (zpravidla opět podle převodní tabulky)
P(r1
< r < r2
) =1 – a kde 
 (převod z1 r1
, z2 r2)
(převod z1 r1
, z2 r2)
intervalový odhad regresní funkce v daném bodě xk (podmíněné střední hodnoty)
(a + bxk – ta n – 2 sy ; a + bxk + ta n – 2 sy )
kde 
Spearmanův koeficient pořadové korelace rs 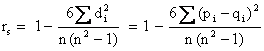
soustava normálních rovnic X´Xb = X´y
index determinace 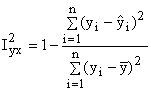
koeficient mnohonásobné determinace 
koeficienty parciální (dílčí)
korelace 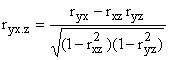
Časové řady
elementární charakteristiky
dyt= yt-yt-1
d(2)yt= dyt-dyt-1
kt= yt/yt-1

soustava normálních rovnic

vzorečky
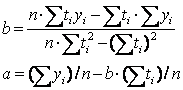
reziduální směrodatná odchylka

index determinace
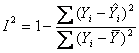
index korelace
I=![]()
testové statistiky

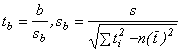
jednoduché exponenciální vyrovnávání
![]()
![]() předpověď
předpověď
sezónní časové řady
sezónní index
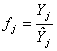
sezónní odchylka
![]()
střední čtvercová chyba
MSE = ![]() , k počet odhadovaných
parametrů
, k počet odhadovaných
parametrů
střední absolutní procentuální chyba
MAPE = 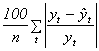
Indexní analýza
bázický
index Ii/0 = ![]() ,
řetězový index Ii/i-1
=
,
řetězový index Ii/i-1
= ![]()
index proměnlivého složení
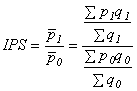
IPS = ISS . ISTR
index stálého složení
 váhy ze základního období ,
váhy ze základního období , 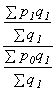 váhy z
běžného období
váhy z
běžného období
index struktury
ISTR = 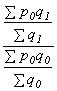 váhy ze základního období , ISTR
=
váhy ze základního období , ISTR
= 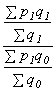 váhy z běžného
období
váhy z běžného
období
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1414
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved