| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Základní pojmy
Vyšetřujeme soustavu m lineárních rovnic o n neznámých ve tvaru:
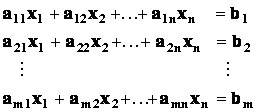
kde aij nazýváme koeficienty ,
xj nazýváme neznámé ,
bi nazýváme pravé strany .
Je‑li bi = 0 i (tj. pro i = 1,2,,m), pak soustavu nazýváme homogenní , jinak nehomogenní.
Soustavu můžeme zapsat v maticovém tvaru:

![]() =
=![]() nebo
nebo ![]()
kde A = je matice
soustavy,
je matice
soustavy,
 je vektor neznámých, a
je vektor neznámých, a 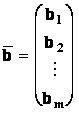 je vektor
pravých stran.
je vektor
pravých stran.
Poznámka : Ekvivalentní úpravy pro SLR jsou úpravy, které převádějí jednu SLR na soustavu se stejnou množinu řešení. Je zřejmé, že jsou totožné s ekvivalentními řádkovými úpravami pro výpočet hodnosti matice.
Sestavme matici ve tvaru: 
Tuto matici značíme ![]() a nazýváme ji rozšířenou maticí soustavy.
a nazýváme ji rozšířenou maticí soustavy.
Gaussova eliminační metoda (GEM) řešení lineárních rovnic
Ekvivalentními
úpravami převedeme matici ![]() na trojúhelníkový tvar (tj. pod hlavní
diagonálou samé nuly). Z takto upravené matice lze okamžitě zjistit h(A) a h(
na trojúhelníkový tvar (tj. pod hlavní
diagonálou samé nuly). Z takto upravené matice lze okamžitě zjistit h(A) a h(![]() ). Přepíšeme‑li tuto upravenou matici
zpětně na soustavu rovnic, můžeme postupně počítat hodnoty neznámých počínaje xn.
). Přepíšeme‑li tuto upravenou matici
zpětně na soustavu rovnic, můžeme postupně počítat hodnoty neznámých počínaje xn.
Věta: Frobeniova
Soustava m lineárních rovnic o n neznámých je řešitelná (tj. má alespoň jedno řešení) právě tehdy, když
h(A) = h(![]() ).
).
Poznámka1 : Soustava nemá žádné řešení
právě tehdy, když h(A) ¹ h(![]() ).
).
Poznámka2 : Je‑li
h(A) = h(![]() ) = n,
) = n,
(kde n je počet neznámých) pak soustava má právě jedno řešení.
Poznámka3 : Je‑li
h(A) = h(![]() ) = h < n,
) = h < n,
pak soustava má nekonečně mnoho řešení, která jsou závislá na volbě (n h) parametrů.
Příklad1: GEM řešte SLR :
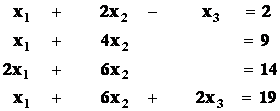
Řešení
![]() =
=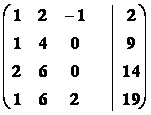


 Þ h(A) = h(
Þ h(A) = h(![]() ) = 3 = n
) = 3 = n
Þ soustava má právě jedno řešení.
x3 = 3 Þ
x2 = 2 Þ x1 = 1 tj. 
Příklad2: GEM řešte SLR :
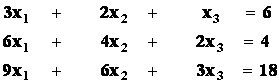
Řešení : ![]() =
=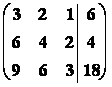
 Þ 1 = h(A) ¹ h(
Þ 1 = h(A) ¹ h(![]() ) = 2
) = 2
Þ soustava nemá řešení.
Příklad3: GEM řešte SLR :

Řešení
![]() =
=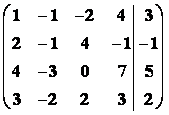
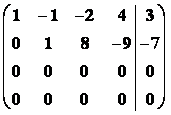 Þh(A) = h(
Þh(A) = h(![]() ) = 2 < n
) = 2 < n
Þ soustava má nekonečně mnoho řešení, která jsou závislá na volbě (n h) parametrů. V tomto případě 4 2=2, čili 2 parametry.
Položíme x4 = s, x3 = r Þ x2 = -7-8r+9s a x1 = -4-6r+5s.
To je 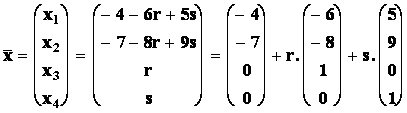 kde r,sIR.
kde r,sIR.
Řešení soustav n lineárních rovnic o n neznámých s regulární maticí soustavy
Věta: Cramerovo pravidlo
Nechť je daná SLR s regulární maticí soustavy A Þ soustava má právě jedno řešení, které můžeme vyjádřit v tvaru

kde 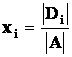 , pro
i = 1,2,,n , přičemž
, pro
i = 1,2,,n , přičemž ![]() je determinant matice, která vznikne
nahrazením i‑tého sloupce matice A sloupcem pravých stran.
je determinant matice, která vznikne
nahrazením i‑tého sloupce matice A sloupcem pravých stran.
Příklad:
Řešte SLR : 
Řešení
 Þ právě jedno řešení, které určíme pomocí CP:
Þ právě jedno řešení, které určíme pomocí CP:
 ,
,  ,
, 
Þ 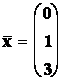
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1185
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved