| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Základy kombinatoriky.
1. Základné pojmy.
Lema 1.1 (Pravidlo súčtu).
Nech A1 .. An
sú disjunktné. Potom ![]() =
=![]() .
.
Dôkaz.
Triviálne.
Lema 1.2 (Pravidlo súčinu).
'A1..An : ![]() =
=![]() .
.
Dôkaz.
Triviálne.
Lema 1.3 (Pravidlo mocniny).
'A,B je počet zobrazení f : A®B rovný |B||A|.
Dôkaz.
Pre každý prvok A môžme vybrať jeho obraz spomedzi prvkov B.
Definícia.
Zobrazenie v : B® sa nazýva variácia s opakovaním n-tej triedy prvkov B.
Triedu variácií s opakovaním označujeme ![]() .
.
Označenie.
Množinu injektívnych
zobrazení z A do b označíme ![]() .
.
Lema 1.4.
Nech |A| = n
a |B| = m. Potom ![]() =
=![]() .
.
Dôkaz.
Obraz prvého prvku A vyberáme z n prvkov, druhého spomedzi n-1, .
Dôsledok 1.1.
![]() =0 Ű |A| > |B|.
=0 Ű |A| > |B|.
Dôkaz.
Triviálne.
Definícia.
Zobrazenia vI![]() nazývame variácie n-tej
triedy z prvkov A. Triedu variácií n-tej triedy označujeme Vn.
nazývame variácie n-tej
triedy z prvkov A. Triedu variácií n-tej triedy označujeme Vn.
Definícia.
Ak |A| = n, tak Vn na A nazývame permutácie na A a označujeme Pn.
Lema 1.5.
Počet usporiadaní n-prvkovej množiny je n!.
Dôkaz.
Triviálne.
2. Relácia ekvivalencie.
Definícia.
j je relácia ekvivalencie n A, ak
'xIA : (x,x)Ij (reflexívnosť)
'x,yIA : (x,y)Ij Ű (y,x)Ij (symetrickosť)
'x,y,zIA : (x,y)Ij Ů (y,x)Ij T (x,z)Ij (tranzitívnosť).
(x,y)Ij označujeme x~y.
Lema 2.1.
Každá relácia ekvivalencie tvorí rozklad množiny na triedy ekvivalencie.
Dôkaz.
Triviálne.
Definícia.
Ak P(B)
je množina podmnožín A, tak množinu Ck(A) =
nazývame kombinácie
k-tej triedy nad A. |Ck(A)| je kombinačné číslo, ktoré zapisujeme ![]() .
.
Veta 2.1.
![]() =
=![]() .
.
Dôkaz.
Triviálne.
Veta 2.2.
Mohutnosť podmnožín každej množiny A je 2|A|.
Dôkaz.
Každý prvok je alebo nie je v danej podmnožine.
3. Základné kombinatorické identity.
Veta
Nech k, n, n1, n2 I
![]() =
= ![]()
![]() =
=![]()
n < k T ![]() = 0
= 0
![]() =
= ![]()
![]() +
+![]() =
=![]()
'xIR : (1+x)n = ![]()
![]() = 0
= 0
![]() = 0.
= 0.
Dôkaz.
Zrejmé.
Lema
Nech A je množina a kIN. Ak j je taká relácia na Vk´(A), že 'f,g : ®A : (f,g)Ij Ű 'xIA : |f-1(x)| = |g-1(x)|, tak j je relácia ekvivalencie.
Dôkaz.
Triviálne.
Definícia.
Triedy rozkladu relácie j z lemy 3.1 nazývame kombinácie s opakovaním k-tej triedy na množine A. Množinu kombinácií s opakovaním k-tej triedy na A označujeme Ck´(A).
Veta 3.2.
|Ck´(A)| = # funkcií f : A®, pre ktoré ![]() =k.
=k.
Dôkaz.
Triviálne.
Veta 3.3.
|Ck´(A)| = ![]() , kde n je
mohutnosť A.
, kde n je
mohutnosť A.
Dôkaz.
Každej kombinácii
jednoznačne prislúcha binárna postupnosť, v ktorej nuly oddeľujú
podpostupnosti jednotiek, pričom počet jednotiek v i-tej podpostupnosti je rovný počtu
opakovaní i-teho prvku z A v kombinácii. Dĺžka postupnosti
je n-k+1, z čoho je práve n
jednotiek. Počet korektných postupností tohoto tvaru je práve ![]() .
.
Veta 3.4.
Nech A,B sú množiny, |A| = n, |B| = k, n = ![]() , A =, B = . Označme
, A =, B = . Označme
![]() počet takých surjekcií f : A®B, že 'iI1..k : |f-1(bi) = ni. Potom
počet takých surjekcií f : A®B, že 'iI1..k : |f-1(bi) = ni. Potom ![]() =
=  .
.
Dôkaz.
Ak n = k, tak sú to permutácie a 'iI1..n : ni = 1. Tých je práve n!. Ak n > k, tak tento počet treba podeliť permutáciami v každej ni (všetky permutácie určujú rovnakú surjekciu).
Veta 3.5.
Nech |A| = k.d. Označme rd počet rozkladov A na d-prvkové množiny.
Potom |rd| = ![]() .
.
Dôkaz.
Každá postupnosť
tried takéhoto rozkladu určuje surjekciu A®B takú, že 'iI1..k : |f-1(bi) = ni. Podľa vety 3.4 je týchto surjekcií . Toto číslo treba ešte vydeliť permutáciami
na triedach rozkladu, ktorých je k!.
. Toto číslo treba ešte vydeliť permutáciami
na triedach rozkladu, ktorých je k!.
4. Polynomická veta.
Veta 4.1 (Polynomická veta).
Nech m,nIN, x1, .. , xnIC. Potom (x1,
.. , xn)n = 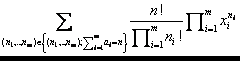 .
.
Dôkaz.
(x1, .. , xn)n = ![]() .
. ![]() , pričom x1
vyberáme
, pričom x1
vyberáme ![]() spôsobmi, x2
spôsobmi, x2
![]() spôsobmi, atď. Spolu
spôsobmi, atď. Spolu  , pričom
, pričom
![]() musí byť n. Priamočiarejší dôkaz je
matematická indukcia.
musí byť n. Priamočiarejší dôkaz je
matematická indukcia.
Veta 4.2.
Počet permutácií,
určených vektorom (x1,
.. , xn), kde 'iI1..n je ki počet
cyklov permutácie dĺžky i, je  .
.
Dôkaz.
n! je počet všetkých permutácií, ki! - poradie cyklov, ![]() - rotačný posun v ki cykloch.
- rotačný posun v ki cykloch.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1519
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved