| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
Nelineární optika a optické solitony
6.1 Dielektrická prostředí (stacionární)
6.2 Nelineární optické jevy
6.3 Optické solitony
6.1 Dielektrická prostředí (stacionární)
Elektromagnetická teorie světla je vyjádřena Maxwellovými rovnicemi:
(pro vakuum)

atd., kde ![]() jsou vektory intenzit
elektrického a magnetického pole;
jsou vektory intenzit
elektrického a magnetického pole;
(pro dielektrické stacionární látkové prostředí)
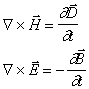
atd., kde ![]() jsou vektory indukcí
elektrického a magnetického pole a dále
jsou vektory indukcí
elektrického a magnetického pole a dále
![]() ,
,
kde ![]() je vektor polarizace.
Lze odvodit
je vektor polarizace.
Lze odvodit
 .
.
Nyní budeme definovat jednotlivé druhy prostředí. Předpokládejme,
že na prostředí působí jako vstupní veličina vektor intenzity
elektrického pole ![]() a výstupní
veličinou je vektor polarizace
a výstupní
veličinou je vektor polarizace ![]() . Prostředí budeme charakterizovat elektrickou
susceptibilitou c, která souvisí s permeabilitou prostředí a indexem lomu vztahem
. Prostředí budeme charakterizovat elektrickou
susceptibilitou c, která souvisí s permeabilitou prostředí a indexem lomu vztahem
![]() .
.
Pro charakterizování jednotlivých prostředí je vhodné zavést následující obrázek

Dielektrické stacionární prostředí nazveme
a) Lineární,
když vektor polarizace závisí lineárně na vektoru intenzity elektrického pole.
b) Nedisperzní,
když odezva je okamžitá. (Vektor intenzity elektrického pole určuje vektor polarizace ve stejném čase.)
c) Homogenní,
když vztah mezi vektorem polarizace a vektorem intenzity elektrického pole nezávisí na prostorových souřadnicích.
d) Izotropní
když vztah mezi vektorem polarizace a vektorem intenzity elektrického pole nezávisí na směru vektoru intenzity (oba vektory jsou navzájem rovnoběžné).
Komplexní vyjádření Maxwellových rovnic
(Zavedení komplexních amplitud):
![]() ,
,
![]() ,
,
kde ![]() jsou komplexní
amplitudy vektorů intenzit elektrického, resp. magnetického pole.
jsou komplexní
amplitudy vektorů intenzit elektrického, resp. magnetického pole.
Maxwellovy rovnice pro komplexní amplitudy (bez časového členu ![]() ) jsou:
) jsou:
![]() ,
,
![]() ,
,
atd. a dále
![]() ,
,
kde ![]() jsou komplexní
amplitudy vektorů indukce elektrického, resp. magnetického pole a vektoru
polarizace.
jsou komplexní
amplitudy vektorů indukce elektrického, resp. magnetického pole a vektoru
polarizace.
Řešením jsou vlnové funkce
![]() ,
,
![]() ,
,
kde ![]() jsou reálné vektory
intenzit elektrického, resp. magnetického pole.
jsou reálné vektory
intenzit elektrického, resp. magnetického pole.
Charakterizujme nyní blíže vybrané druhy prostředí.
Charakteristika nehomogenního prostředí (jinak: dielektrického, stacionárního, lineárního, nedisperzního, izotropního).
Je důležité si uvědomit, že ![]() ,
,
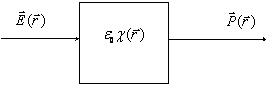
Charakteristiku prostředí vyjadřuje vztah
![]() .
.
Charakteristika anizotropního prostředí (jinak: dielektrického, stacionárního, lineárního, nedisperzního, homogenního).

Jednotlivé souřadnice vektoru polarizace jsou
![]() ,
,
kde ![]() jsou složky tenzoru elektrické susceptibility. Například
jsou složky tenzoru elektrické susceptibility. Například
![]() .
.
Symbolicky lze vektor polarizace vyjádřit
 ,
,
![]() ,
,
kde ![]() je tenzor elektrické
susceptibility. Charakter tenzoru bude mít také index lomu prostředí
je tenzor elektrické
susceptibility. Charakter tenzoru bude mít také index lomu prostředí ![]() .
.
Charakteristika disperzního prostředí (jinak: dielektrického, stacionárního, lineárního, homogenního, izotropního).
(![]() )
)

kde e c n) je přenosová funkce (lineární soustavy). Lze vyjádřit
![]() .
.
Rozdíl mezi nedisperzním a disperzním prostředím spočívá v tom, že v disperzním prostředí elektrická susceptibilita závisí na frekvenci
![]() .
.
V časové oblasti platí konvoluce
 ,
,
kde
![]() .
.
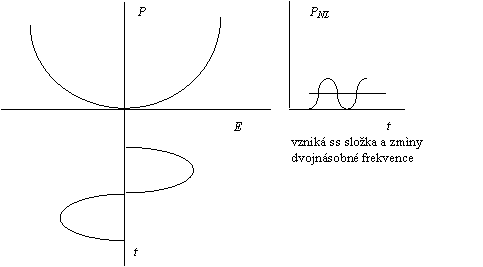
Charakteristika nelineárního prostředí (jinak: dielektrického, stacionárního, nedisperzního, homogenního, izotropního).
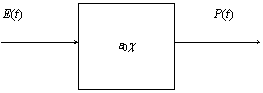
Dosáhne-li intenzita elektrického pole hodnoty srovnatelné s hodnotou intenzity pole uvnitř atomu, tj. 105 V.m-1, nastane mezi E(t) a P(t) nelineární závislost. Graficky

V okolí E = 0 lze funkční závislost P na E rozvinout v Taylorovu řadu
![]()
Po dosazení je
![]() ,
,
kde ![]() je koeficient
nelinearity 2. řádu [C.V-2] a
je koeficient
nelinearity 2. řádu [C.V-2] a ![]() je koeficient
nelinearity 3. řádu [C.m.V-3].
je koeficient
nelinearity 3. řádu [C.m.V-3].
(Pro úplnost: [![]() ] = 1; [P] = C.m-2; [E] = V.m-1.)
] = 1; [P] = C.m-2; [E] = V.m-1.)
Zápis funkční závislosti P na E lze zjednodušit do tvaru
![]() ,
,
kde PL je lineární a PNL nelineární složka elektrické
polarizace. ![]()
6.2 Nelineární optické jevy
Nelineární optické jevy druhého řádu. (Generace druhé harmonické.)
(![]() )
)
Nelineární optické jevy třetího řádu. (Generace třetí harmonické, optický Kerrův jev a automodulace fáze.)
(![]() )
)
Účinnost generace třetí harmonické je ve většině
případů velmi malá a není notno se jí na tomto místě zabývat.
Pro analýzu dalších nelineárních jevů je vhodném si uvědomit, že
nelineární prostředí vyvolává závislost indexu lomu na intenzitě
procházejícího optického záření ![]() . Tuto závislost lze aproximovat lineárním vztahem
. Tuto závislost lze aproximovat lineárním vztahem
![]() (optický Kerrův
jev).
(optický Kerrův
jev).
Pro změnu indexu lomu vzvolanou nelinearitou prostředí platí
![]() ,
,
kde Z0 je impedance vakua (377 W), n je index lomu prostředí a n2 se nazývá nelineárním indexem lomu [m2.W-1].
V důsledku optického Kerrova jevu dochází při šíření vlny k automodulaci fáze. Pro fázi vlny šířící se prostředím délky L platí vztah
![]() ,
,
kde P je střední přenášený výkon plochou příčného průřezu A. Pro změnu fáze platí tedy vztah
![]() ,
,
kde k0 je vlnové číslo ve vakuu. Je-li l = 1000 nm; L = 1 m; A =10-2 mm2; n2 = 10-14 m2.W-1 (sklo) a P = 0,5 mW, změní se fáze o p
6.3 Optické solitony
Šíří-li se impuls optického záření disperzním (lineárním) prostředím, mění se jeho tvar. Předpokládejme jednomodové optické vlákno vykazující pouze vlnovodnou disperzi. Jednotlivé frekvenční složky, z nichž se impuls optického záření skládá, se šíří různými grupovými rychlostmi a dojde k časovému rozšiřování impulsu. Předpokládejme navíc nelineární optické vlákno vykazující optický Kerrův jev. Při šíření vlny takovým vláknem se bude navíc měnit fáze a tudíž i frekvence.
Působení nelinearity na změnu frekvence
(fáze)
![]() ,
,
(okamžitá frekvence)
![]() .
.
Časové rozložení intenzity v impulsu lze znázornit
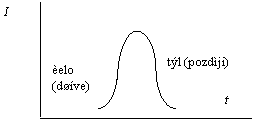
V části impulsu, kde ![]() (nazveme ji „týlem“),
okamžitá frekvence vzrůstá (nastává tzv. „modrý posuv“). V části
impulsu, kde
(nazveme ji „týlem“),
okamžitá frekvence vzrůstá (nastává tzv. „modrý posuv“). V části
impulsu, kde ![]() (nazveme ji
„čelem“), okamžitá frekvence klesá (nastává tzv. „rudý posuv“). Graficky:
(nazveme ji
„čelem“), okamžitá frekvence klesá (nastává tzv. „rudý posuv“). Graficky:

Vliv vlnovodné disperze
Stručně: Platí ![]() . Bude-li disperzní koeficient kladný
. Bude-li disperzní koeficient kladný ![]() (anomální disperze),
pak při narůstání vlnové délky bude grupová rychlost v klesat. Schematicky:
(anomální disperze),
pak při narůstání vlnové délky bude grupová rychlost v klesat. Schematicky:
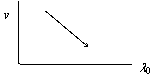
Důsledkem je, že část impulsu s větší okamžitou frekvencí (kratší vlnovou délkou) se šíří rychleji než část impulsu s menší okamžitou frekvencí. Oblast modrého posuvu „dobíhá“ oblast rudého posuvu. Týl impulsu se šíří rychleji než jeho čelo a dochází k časovému stlačování (kompresi) impulsu.
Při určité hodnotě intenzity a při určitém tvaru impulsu se účinek vlnovodné disperze vyrovnává působením nelineárního jevu automodulace fáze a prostředím se šíří impuls beze změny tvaru. Takovému stabilnímu impulsu se říká „soliton“.
Solitony jsou mody (vlastní funkce) nelineárního dispersního systému. Matematická analýza vychází z nelineární vlnové rovnice
![]() .
.
Řešením jsou vlny
![]()
s komlexní obálkou
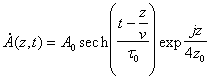 .
.
Obálkou solitonu je symetrická zvonovitá funkce šířící se rychlostí v. Maximální hodnota je A0, šířka je t (pološířka amplitudy) a plocha je 2pA t . Při solitonovém provozu se podařilo přenášet solitony šířky 10 ps na vzdálenost několika tisíc kilometrů.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1356
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved