| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Rezonanční transformátor

Schéma zapojení rezonančního transformátoru je nakresleno na obr. 1. Budící impulsy pro feritový transformátor vyrábí impulsní LC oscilátor, tvořený řídicí elektronikou, cívkou L1 a kondenzátorem C1. Cívka L1 zároveň tvoří primární vinutí fritového transformátoru. Na sekundární cívku L2 transformátoru je připojen kondenzátor C2. Pro správnou funkci rezonančního transformátoru je nutné, jak již vyplývá z názvu, aby primár transformátoru byl v rezonanci se sekundárem. To znamená, že rezonanční kmitočet sekundární cívky L2 a kondenzátoru C2 se musí rovnat, nebo být celistvým násobkem rezonančního kmitočtu primáru. Platí tedy:
1 1
------------- = k ----- ----- -------- , pro k = 1, 2, 3,… (1)
2p (L1C1) 2p (L2C2)
Po úpravě dostaneme tuto rovnici:
L1C1 = k2 L2C2 (2)
Odtud získáme vzorec pro výpočet velikosti kondenzátoru C2:
C1 L1
C2 = ---------- (3)
k2 L2
Víme, že indukčnost cívky je přímo úměrná druhé mocnině počtu závitů N. Vzorec (3) můžeme tedy přepsat na tvar
C1 N1
C2 = ------ (-----)2 (4)
k2 N2
Poznámka: Jak dále uvidíme,
situace v rezonančním transformátoru je trochu složitější. Přesto praxe
ukázala, že vzorce (3) a (4) jsou užitečné (alespoň pro k = 1, 2).
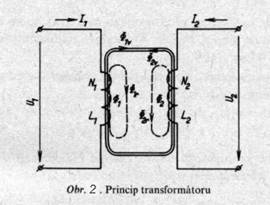
Nyní si řekneme něco málo o teorii transformátorů. Transformátor tvoří dvě cívky (nebo více cívek), které jsou vázány společným magnetickým tokem (obr. 2). Je-li primární cívka připojena ke zdroji střídavého napětí U1, protéká jejím vinutím proud I1, který vybudí magnetický tok F , který má dvě složky: vazební Fv a rozptylovou Fr. Vazební složka mag. toku se uzavírá sekundárním vinutím, v němž indukuje napětí U2. Působením indukovaného napětí U2 protéká uzavřeným sekundárním obvodem proud I2, který v cívce vybuzuje magnetický tok F F2v F2r. Vazební složka se uzavírá závity primární cívky. Vinutí primární a sekundární cívky jsou vázána společným magnetickým tokem, který je dán rozdílem obou vazebních toků:
Fv F1v F2v (5)
Tomuto toku odpovídá vazební indukčnost Lv, která je dána poměrem vazebního toku Fv a proudu I1 procházejícího primární cívkou.
Fv
Lv = ------- (6)
I1
U1 4,44 f Fv N1 N1
------ = ----- ----- -------- = ------ = p (7)
U2 4,44 f Fv N2 N2
Vztah mezi proudy se u ideálního, bezeztátového transformátoru odvodí z rovnosti výkonů:
P1 = P2
U1I1 = U2I2
I1 U2 N2 1
(8)
I2 U1 N1 p
Závislost mezi magnetickým tokem cívky a její indukčností (6) umožňuje nahradit primární a sekundární cívku transformátoru sériovým zapojením vazební a rozptylové cívky:
L1 = L1v + L1r (9a)
L2 = L2v + L2r (9b)
Vztah mezi celkovou indukčností cívky a její vazební složkou se udává pomocí činitele vazby k:
L1v L2v
k = ------ = ------- (10)
L1 L2
Na přenosu energie se podílejí pouze vazební indukčnosti. Jejich geometrická střední hodnota se rovná činiteli vzájemné indukčnosti M:
______ ________
M = L1vL2v = kL1 kL2
_____
M = k L1L2 (11)
L1r = L1 – L1v = L1 – kL1 = L1(1 - k)
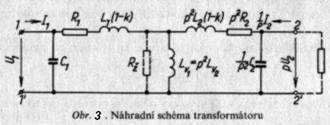
Na obr. 3 je nakresleno náhradní schéma transformátoru. Všimněte si, že prvky sekundární části transformátoru se přepočítávají na transformátor o převodu p = 1. Tento způsob má své fyzikální zdůvodnění, neboť přepočítáváním se velikosti veličin převádějí na hodnoty, kterými ovlivňují primární obvod.
Na základě tohoto náhradního schématu si pro naše účely vytvoříme zjednodušené náhradní schéma rezonančního transformátoru, které najdete na obr. 4.
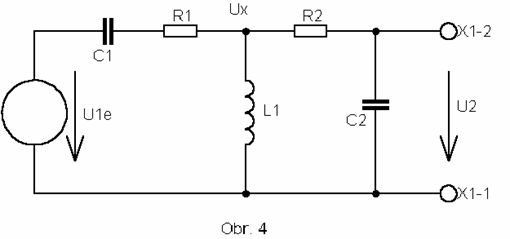
V tomto schématu jsme zanedbali ztráty v železe, rozptylové indukčnosti a kapacitu primárního vinutí. Pro jednoduchost také předpokládáme, že převod p = 1.
Obvod z obr. 4 budeme řešit standardními metodami teorie obvodů. Pro odvození napěťového přenosu se lépe hodí metoda uzlových napětí. Pomocí této metody sestavíme obvodové rovnice:
U1 - Ux Ux Ux – U2
----- ----- ------ = ------ + -----------
R1 + 1/pC1 pL R2
Ux – U2
----------- = U2pC2
R2
Rovnice upravíme do tvaru:
U1 = (R1 + 1/pC1)(Ux(1/pL – 1/R2) – U2/R2) + Ux
Ux =U2(pR2C2 + 1)
V první rovnici dosadíme za Ux a po úpravách dostaneme výsledný vztah pro přenos:
U2 p2LC1
U1 p3LC1C2(R1 + R2) + p2(R1R2C1C2 + L(C1 + C2)) + p(R1C1 + R2C2) + 1
Označíme:
A = LC1
C R1R2C1C2 + L(C1 + C2)
D = R1C1 + R2C2
A dostaneme tento tvar Laplaceova přenosu:
U2 p2A
U1 p3B+ p2C + pD + 1
Za operátor p dosadíme jw a dostaneme frekvenční přenos:
U2(jw -w A -w A
U1(jw -jw B - w C + jwD + 1 (1- w C) + j(wD - w B)
U2(jw) w A[(w C - 1) + j(D - w B)w
(12)
U1(jw) (1- w C)2 + (D - w B)2w
D - w B = 0 (13)
Tím se nám frekvenční přenos (12) zjednoduší na:
U2(jw) w A
pro w wrez (14)
U1(jw) 1- w C
R1 C1 + R2 C2 = w C1 C2 L (R1 + R2),
odkud
R1 C1 + R2 C2
w (15)
C1 C2 L (R1 + R2)
V případě, že R1 = R2, což se dá u transformátoru s převodem p = 1 předpokládat, zjednoduší se výraz (15) na tvar
1
w (16)
2 L Cx
kde Cx je kapacita kondenzátorů C1 a C2 zapojených v sérii:
C1 C2
Cx = ----------- (17)
C1 + C2
Naopak, pokud C1 = C2 = C, potom dostaneme standardní vzorec pro rezonanční kmitočet:
1
w
L C
Nyní dosadíme za proměnné A a C ve vzorci pro přenos (14):
U2 w LC1
-------- = -------- ----- ------ ------- pro w wrez (18)
U1 1- w (R1R2C1C2 + L(C1 + C2))
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1204
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved