| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ
Fakulta Elektrotechnická
Systémy a modely
Rozpoznání systému HELIKOPTÉRA 2
Úkolem je identifikovat systém tvořený vstupem napětí na pomocný rotor, přičemž výstupem je azimut vrtulníku.
Nákres systému:

Popis obrázku:
T - Těžiště vrtulníku
F1 – Síla vyvolaná od točivého momentu hlavního rotoru
F1’ – Síla vyvolaná zadním rotorem (tato síla vyrovnává působení síly F1 v pracovním bodě vrtulníku).
F2 – Síla vyvolaná zvýšením napětí na zadním rotoru oproti ustálené hodnotě (v pracovním bodě vrtulníku).
M1 – Moment vyvolaný účinkem síly F1, M1 = F1 . r1
M1 – Moment vyvolaný působením síly F1’ (momenty M1 a M1 se sobě rovnají)
Další vyplývající vztah:
Ms – Setrvačný moment hmoty vrtulníku. (Působí proti silám snažícím se otáčet vrtulníkem. Je dán vztahem Ms = Is . e, kde e je úhlové zrychlení a Is je setrvačný moment)
Pro náš případ byl vrtulník zaaretován ve vodorovné poloze a mohl se otáčet pouze kolem své svislé osy. Hlavní rotor tedy neměl funkční vliv na elevaci vrtulníku a sloužil pouze k vyvození síly F1 (potažmo momentu M1) a tedy k nastavení pracovního bodu systému.
Pokud síla F1’ je tak velká, že M1 = M1’, tedy F1 . r1 = F1’ . r2, tak se model vrtulníku neotáčí - toto je výsledkem nastavení pracovního bodu.
V našem případě byl pracovní bod zvolen následovně: Napětí na motoru hlavního rotoru bylo 0,6 a motoru zadního rotoru 0,13. Při těchto hodnotách setrvával model vrtulníku v klidu a nedocházelo k jeho otáčení.
Pokud dojde ke změně napětí motoru zadního rotoru o DU, pak začne působit síla F2, která má za následek vyvození momentu M2 a tím porušení rovnováhy systému - vrtulník se tedy začne otáčet.
Síla F2 je při tom úměrná té to změně napětí: F2 = k1(t) . DU, kde k1(t) je konstanta úměrnosti mezi změnou napětí a působící sílou. Jelikož je zadní rotor fyzikální těleso s působením momentu setrvačnosti apod. není změna otáček rotoru skoková a tím ani změna síly není skoková. Proto je k1 závislá na čase.
Působící síla F2 začne vyvozovat moment M = F2 . r2 , lze tedy psát M = k1(t). DU. r2.
Zjednodušíme tuto rovnici zavedením konstanty k(t) = k1(t). r2, pak tedy M = DU . k(t).
V otáčení modelu vrtulníku ale brání brzdný moment, který je úměrný rychlosti otáčení (tedy úhlové rychlosti) w a dále setrvačný moment MS. Lze tedy psát, že: MB = B.w, kde B je konstanta úměrnosti brzdného momentu.
Systém lze tedy popsat rovnicí:
![]() (1)
(1)
Po dosazení za momenty:
![]() (2)
(2)
Působící moment M, jak již bylo zmíněno výše, je časově závislý, neboť fyzikální vlastnosti zadního rotoru vrtulníku nedovolují jeho skokovou změnu se změnou napětí. Předpokládali jsme jeho chování jako chování systému 1. řádu, tedy:
![]() , (3)
, (3)
kde t představuje zpoždění tohoto podsystému.
Pro jednoduchost uvažujme nyní podsystém zadního rotoru vrtulníku za ideální s odezvou M = k . DU (bez časové závislosti). (4)
Pak bude Laplaceova transformace rovnice (2) vypadat následovně:
![]() (5)
(5)
Pro sestavení
přenosu bude k.DU představovat jednotkový skok - jeho
Laplaceova trasformace je ![]() . (6)
. (6)
Přenos systému podle (5) a (6) tedy bude:
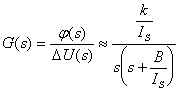 (7)
(7)
Toto lze
upravit zavedením nové konstanty ![]() na jednodušší tvar: (8)
na jednodušší tvar: (8)
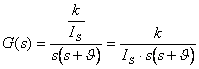 (9)
(9)
Neboť zadní rotor vrtulníku nemá takto ideální přenos, provedeme zahrnutí jeho nezjednodušeného přenosu do rovnice (9).
Nejprve provedením Laplaceovy transformace rovnice (3):
![]() (10)
(10)
Dosazením transformace jednotkového skoku (6) za změnu DU dostaneme:
![]() (11)
(11)
Spojením rovnic (11) a (9) (a vynecháním konstanty k z rovnice (11), neboť se jedná o totéž k, které je již zahrnuto v rovnici (9) původně uvažovaného ideálního podsystému) dostaneme:
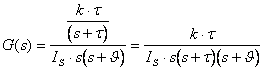 (12)
(12)
Vztah (12) zjednodušíme zavedením nové konstanty K:
![]() (13)
(13)
Dostaneme tedy:
![]() (14)
(14)
Stavové rovnice vyjádříme nejprve pro zjednodušený případ podle (4), tedy pro ideální odezvu zadního rotoru vrtulníku:
Vyjdeme z tvaru rovnice (2) upravené podle výše zmíněné podmínky na tvar (5):
Základním předpokladem je substituce:
![]()
![]() (15)
(15)
Dosazením získáme:
![]()
![]() (16)
(16)
Z toho dosazením za J a K:
![]()
![]() (17)
(17)
Normalizovaný tvar stavových rovnic:
![]()
![]() (18)
(18)
Pak porovnáním tvaru (18) s tvarem (17) dostáváme:
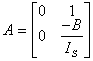

![]()
![]() (19)
(19)
Pro nezjednodušený model podsystému zadního rotoru vyjdeme z rovnice (14) a jejího převedení do časové oblasti:
![]() (20)
(20)
Vztah zjednodušíme zavedením substituce V = K.t (21)
![]() (22)
(22)
Řešit budeme obdobně jako pro zjednodušení model:
tj. provedeme substituci:
![]()
![]()
![]() (23)
(23)
Dosazením získáme:
![]()
![]()
![]() (24)
(24)
Stavová rovnice (po porovnání s norm. tvarem) a přepisem do maticového tvaru je:
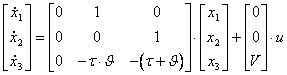
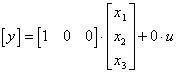 (25)
(25)
Pro zjednodušující případ ideální odezvy podsystému zadního rotoru vrtulníku můžeme uvažovat, že úhlové zrychlení e je přímo funkcí změny napětí U. Model vrtulníku by pro takový případ vypadal takto:
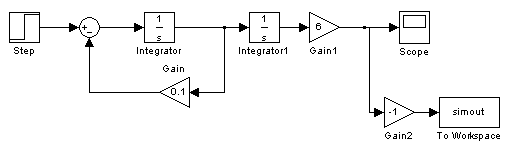
Toto schéma odpovídá stavu, kdy po příchodu skokové změny napětí na motor zadního rotoru vrtulníku je tento model přidržen ve stálé poloze do doby, než se rotor vrtulníku roztočí na otáčky odpovídající novému napětí a změna polohy je uvažována až od doby jeho uvolnění. V měřených charakteristikách se tedy neprojevuje postupně narůstající síla F2, ale model se chová tak, jako by se tato síla měnila skokově ihned. Tomuto chování odpovídá rovnice (9).
U reálného vrtulníku není změna síly F2 skoková, ale mění se postupně podle rovnice (3). Model reálného vrtulníku tedy vychází z rovnice (12) a vypadá takto:

Zesílení zesilovače „Gain“ odpovídá hodnotě J t, zesílení „Gain2“ pak hodnotě K.t, pdle rovnice (21), resp (24).
Nejprve bylo nutno stanovit pracovní bod modelu, neboť pro malé změny napětí zaního rotoru v blízkosti nulového napětí (nulových otáček) je chování motoru silně nelineární.
Hodnoty pracovního bodu byly stanoveny takto:
Napětí hlavního rotoru: UHR = 0,6V
Napětí zadního rotoru vyrovnávající moment působený hlavním rotorem: UZR = 0,13V
K nalezení konstant K a J bylo použito zjednodušeného modelu vrtulníku.
Konstanty byly stanoveny tak, aby průběh odezvy na skok změny napětí motoru zadního rotoru vrtulníku byl totožný v simulovaném modelu a reálném systému.
Pro konstanty J = 0,1 a K = 6,0 a skokovou změnu napětí U = 0,2V byly změřeny a odsimulovány následující charakteristiky:
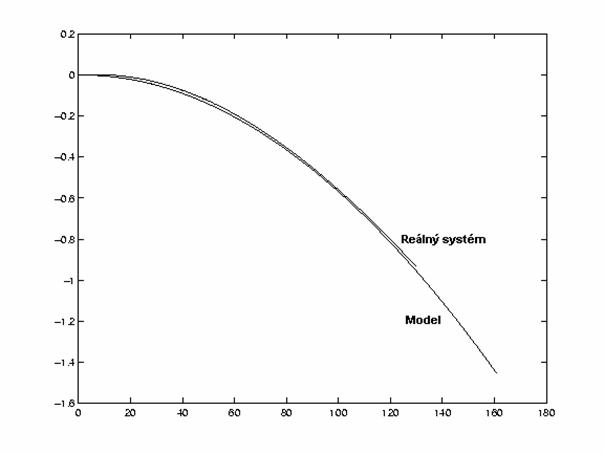

Pro stanovení zbývající konstanty t, tedy
časového zpoždění působící síly F2, bylo použito
úplného modelu vrtulníku.
Pro hodnotu t = 2,3 byly změřeny druhé charakteristiky na předchozí straně.
Pomocí těchto konstant můžeme jejich dosazením do rovnice (25) psát výsledné stavové rovnice:

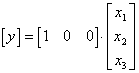
Porovnání přechodových charakteristik obou modelů systému (tj. se skokovou změnou síly F2 a s pozvolnou změnou F2):

Pomocí modelu Simulinku jsme stanovili dále síť přechodových charakteristik pro různě velké změny napětí U na motoru zadního rotoru vrtulníku:
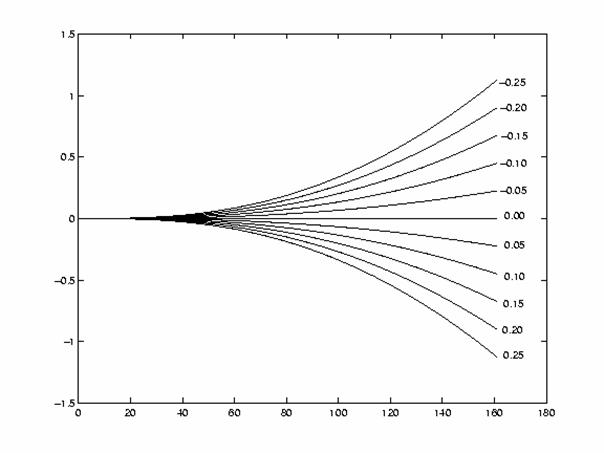
Podle předloženého modelu vrtulníku byl stanoven fyzikální a matematický popis chování tohoto systému na zadanou změnu vstupního parametru - tj. změnu napětí na motoru zadního rotoru.
Nejzdlouhavější částí práce bylo nalezení vhodných konstant K, J a t tak, aby matematicko-fyzikální model měl stejnou časovou odezvu na tuto změnu jako reálný systém.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1025
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved