PERCEPTRON

1. In 1957, Rosenblatt and several other researchers developed perceptron, which used the similar network as proposed by McCulloch, and the learning rule for training network to solve pattern recognition problem.

(*) But,this model was later criticized by Minsky who proved that it cannot solve the XOR problem.

2. The network structure:

3. The training process:

Choose the network layer,nodes,& connections

Randomly assign weights: W & bias:

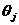
Input training sets X (preparing T for verification )

Training computation:

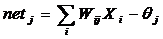
(7) Recall : after the network has trained as mentioned above, any input vector X can be send into the perceptron network. The trained weights, , and the bias, , is used to derive and, therefore, the output can be obtained for pattern recognition.

Ex: Solving the OR problem

Let the training patterns are used as follow.

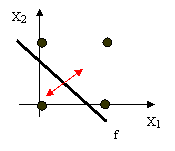
X1 X2	T
0 0	0
0 1	1
1 0	1
1 1	1

Let W₁₁=1, W₂₁=0.5, Θ=0.5

The initial net function is:

net = W₁₁X₁+ W₂₁X₂-Θ η=0.1

　 net = 1X₁₁ + 0.5X₂₁ - 0.5

Feed the input pattern into network one by one

(0,0), net= -0.5, Y=0, δ= 0 O.K.

(0,1), net= 0, Y= 0, δ=1- =1 (need to update weight)

(1,0) net= 0.5, Y=1, δ= 0 O.K.

(1,1) net= 1, Y=1, δ= 0 O.K.

update weights for pattern (0,1) which is not satisfying the expected output:

ΔW₁₁=(0.1)(1)( 0)= 0, ΔW₁₂=(0,1)(1)( 1)= 0.1, ΔΘ=-(0.1)(1)=-0.1

W₁₁= W₁₁₊ΔW₁₁₌1, W₂₁=0.5+0.1=0.6, Θ=0.5-0.1=0.4

Applying new weights to the net function:

net=1X₁+0.6X₂-0.4

Verify the pattern (0,1) to see if it satisfies the expected output.

(0,1), net= 0.2, Y= 1, δ=

Feed the next input pattern, again, one by one

(1,0), net= 0.6, Y=1, δ=

(1,1) , net= 1.2, Y=1, δ=

Since the first pattern(0,0) has not been testified with the new weights, feed again.

(0,0), net=-0.4, Y=, δ=

Now, all the patterns are satisfied the expected output. Hence, the network is successfully trained for understanding the OR problem(pattern).

We can generate the pattern recognition function for OR pattern is:

net= X₁ + 0.6X₂ - 0.4 (This is not the only solution, other solutions are possible.)

The trained network is formed as follow:

Recall process:

Once the network is trained, we can apply any two element vectors as a pattern and feed the pattern into the network for recognition. For example, we can feed (1,0) into to the network

(1,0), net= 0.6, Y=1 Therefore, this pattern is recognized as 1.

Ex: Solving the AND problem (i.e., recognize the AND pattern)

Let the training patterns are used as follow.

X1 X2	T
0 0	0
0 1	0
1 0	0
1 1	1

Let W₁₁=0.5, W₂₁=0.5, Θ=1, Let η=0.1

The initial net function is:

net　=0.5X₁₁+0.5X₂₁ 1

Feed the input pattern into network one by one

(0,0), net=-1 Y=, δ=

(0,1), net=-0.5 Y= , δ=

(1,0) net=- 0.5, Y= , δ=

(1,1) net= , Y= , δ= 1

update weights for pattern (1,1) which does not satisfying the expected output:

ΔW₁₁=(0,1)(1)( 1)= 0.1, ΔW₂₁=(0,1)(1)( 1)= 0.1,

ΔΘ=-(0.1)(1)=-0.1

W₁₁=0.6, W₂₁=0.5+0.1=0.6, Θ=1-0.1=0.9

Applying new weights to the net function:

net=0.6X₁ + 0.6X₂ - 0.9

Verify the pattern (1,1) to see if it satisfies the expected output.

(1,1) net= 0.3, Y= 1 , δ=

Since the previous patterns are not testified with the new weights, feed them again.

(0,0), net=-0.9 Y=, δ=

(0,1), net=-0.3 Y= , δ=

(1,0) net=- 0.3, Y= , δ=

We can generate the pattern recognition function for OR pattern is:

net= 0.6X₁ + 0.6X₂ - 0.9 (This is not the only solution, other solutions are possible.)

The trained network is formed as follow:

Ex: Solving the XOR problem

Let the training patterns are used as follow.

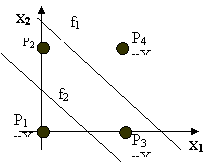
X1 X2	T
0 0	0
0 1	1
1 0	1
1 1	0

Let W₁₁=1.0, W₂₁= -1.0, Θ=0,

If we choose one layer network, it will

be proved that the network cannot be

converged. This is because the XOR

problem is a non-linear problem, i.e.,

one single linear function is not enough

to recognize the pattern. Therefore, the

solution is to add one hidden layer for extra

functions. The following pattern is formed.

X1 X2	T1 T2	T3
0 0	0 0	0
0 1	0 1	1
1 0	0 1	1
1 1	1 1	0

Let W₁₁=0.3, W₂₁=0.3, W₁₂= 1, W₂₂= 1

The initial net function for node f1 and node f2 are:

f₁ = 0.3X₁₁+ 0.3X₂₁ - 0.5

f₂ = 1X₁₂+ 1X₂₂ - 0.2

Now we need to feed the input one by one for training the network.for f1 and f2 seprearately. This is to satisfiying the expected output for f1 using T1 and for f2 using T2.

Finally, we use f1 and f2 as input pattern to train the node f_3, the result is

f₃=1X₁₃ - 0.5X₂₃ + 0.1