Produire des images, observer

Formation d’une image

Image formée par une lentille mince convergente

Dans la construction graphique, on orientera l’axe optique principal, choisi comme axe des abscisses, dans le sens de la propagation de la lumiÈre.

Les propriétés des trois rayons particuliers sont :

le rayon incident passant par le centre optique O n'est pas dévié

le rayon incident parallÈle à l'axe optique émerge en passant par le foyer image F’

le rayon incident passant par le foyer objet F donne un rayon émergent parallÈle à l'axe optique

Construction graphique d’une image d’un objet plan perpendiculaire à l’axe optique

L’image cherchée est, comme l’objet, perpendiculaire à l’axe optique. De plus, son extrémité A’ est sur cet axe puisque le rayon AO traverse la lentille sans subir de déviation.

Tous les rayons issus du point objet B qui traversent la lentille (faisceau grisé) convergent au point B’.

Construction graphique d’une image d’un point objet situé à l’infini

Quand une source ponctuelle est à l’infini (comme l’est pratiquement une étoile), les rayons qui en partent sont parallÈles.

Relation de conjugaison sous forme algébrique et grandissement

Relation de conjugaison des lentilles minces convergentes :

On appelle distance focale (image) f’ d’une lentille la distance algébrique du centre optique O de la lentille au foyer (image) :

La vergence C d’une lentille exprimée en dioptries (d) est définie par  avec f’ exprimée en mÈtre.

On appelle grandissement g le rapport algébrique

Validité de cette étude : conditions de Gauss

Un systÈme est utilisé dans les conditions de Gauss s’il n’est traversé que par des rayons faisant un angle faible avec l’axe du systÈme (rayons paraxiaux). Toutes les grandeurs et formules introduites ne sont valables que dans ces conditions. Ces conditions de Gauss sont considérées comme remplies si les qualités de l’image obtenue sont compatibles avec le “pouvoir de résolution” du récepteur (pixels, grain de la pellicule photo…).

Les conditions de Gauss ne sont pas systématiquement remplies et l’image obtenue peut Être déformée (œilleton, objectif grand angle) ou non (objectif photographique normal…).

Image formée par un miroir sphérique convergent

Le miroir est une calotte sphérique de centre C et de rayon R. Le foyer F’ se situe au milieu du segment CS tel que . La distance focale est .

Les propriétés des trois rayons particuliers sont :

le rayon incident passant par le centre optique C se réfléchit sur lui-mÊme

le rayon incident parallÈle à l'axe optique se réfléchit en passant par le foyer image F’

le rayon incident passant par le foyer image F’ se réfléchit parallÈlement à l'axe optique

Construction graphique de l’image d’un objet plan perpendiculaire à l’axe optique principal

L’objet et son image sont perpendiculaires à l’axe optique. A et A’ sont sur cet axe puisque le rayon AS passe par le centre C et se réfléchit sur lui-mÊme.

Construction graphique de l’image d’un point objet situé à l’infini

L’image d’un point objet B situé à l’infini est située dans le plan focal image du miroir.

Conditions de Gauss

Tous les rayons incidents parallÈles à l'axe optique principal qui se réfléchissent sur le miroir ne convergent pas en un point unique (ce défaut du miroir sphérique est connu sous le nom d'aberration de sphéricité).

Le modÈle du miroir sphérique ci-dessus n’est donc valide que dans les conditions de Gauss.

Quelques instruments d’optique

Le microscope

Un microscope comprend deux systÈmes optiques appelés objectif et oculaire.

L'objectif, placé prÈs de l'objet à examiner, donne de celui-ci une image fortement agrandie.

L'oculaire, derriÈre lequel se place l’œil, joue le rôle d'une loupe dans l'examen de l'image fournie par l'objectif.

Ces deux systÈmes optiques sont maintenus à une distance invariable l'un de l'autre par fixation aux extrémités d'un tube métallique.

L'objet est examiné par transparence ; il faut alors l'éclairer fortement en concentrant sur lui la lumiÈre au moyen d'un miroir orientable, associé souvent à un systÈme optique convergent appelé condenseur.

Modélisation par un systÈme de deux lentilles

L’objectif est une lentille de faible diamÈtre et de trÈs petite distance focale (quelques mm). L’image intermédiaire A₁B₁ donnée par l’objectif constitue un objet pour l’oculaire. L’image finale A’B’ qu’observe l’œil est renversée.

La distance fixe  D = s’appelle la longueur optique du microscope. Elle est voisine de 16 cm dans tous les microscopes modernes.

Le cercle oculaire et la position de l’œil

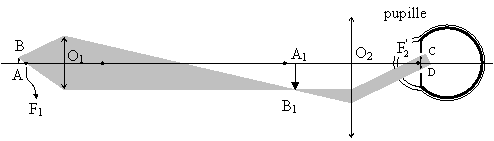
Tous les rayons lumineux issus de l’objet et qui traversent le microscope passent, à la sortie, à l’intérieur d’un cercle de diamÈtre CD que l’on appelle le cercle oculaire. Son diamÈtre est toujours inférieur à celui de la pupille de l’œil. L’œil dont la pupille est dans le plan de ce cercle reçoit toute la lumiÈre qui traverse le microscope.

Le grossissement standard G

Pour un microscope, on peut le définir par le rapport du diamÈtre apparent de l’image finale b au diamÈtre apparent de l’objet observé à l’œil nu à la distance minimale de vision distincte a

La distance minimale de vision distincte (appelée punctum proximum noté d _m) est égale à 25 cm pour l’œil normal.

(1)

L’image finale (A’B’) est à l’infini (A’_¥ B’_¥) quand l’image intermédiaire A₁B₁ est dans le plan focal objet de l’oculaire (mise au point à l’infini). Cette position est avantageuse pour l’œil normal puisqu’elle supprime la fatigue de l’accommodation.

(2)

Les triangles et sont semblables : (3)

(1), (2) et (3) :

Exemple numérique

D = 16 cm f’₁ = 2 mm f’₂ = 2,5 cm d _m = 0,25 m pour un œil normal

A travers ce microscope un objet serait vu, sans accommoder, sous un angle 800 fois plus grand

La lunette astronomique

Une lunette comprend deux systÈmes optiques convergents de mÊme axe : un objectif et un oculaire.

L'objectif peut Être assimilé à une lentille mince convergente de grand diamÈtre d'ouverture D (entre 20 cm et 1 m) et de grande distance focale f ₁ (15 à 20 fois ce diamÈtre D).

L'oculaire joue le rôle d'une loupe dans l'examen de l’image fournie par l’objectif (c’est généralement un systÈme de deux lentilles).

Modélisation de la lunette astronomique par un systÈme afocal de deux lentilles minces

Comme dans le cas du microscope, l’image finale A’B’ est renversée par rapport à l’objet AB.

Le cercle oculaire est situé au-delà et trÈs prÈs du plan focal image de l’oculaire.

Le plan focal objet F₂ de l’oculaire coÃ�ncide avec le plan focal image F’₁ de l’objectif. Dans ce cas, un faisceau incident cylindrique est transformé par la lunette en un autre faisceau cylindrique. On dit que la lunette est  afocale. L’image finale est rejetée à l’infini ; ceci permet d’éviter la fatigue de l’accommodation de l’œil de l’observateur.

(4)

(5)

Le grossissement standard

On appelle grossissement d'une lunette le rapport du diamÈtre apparent de l'image finale au diamÈtre appa­rent de l'objet observé à l'œil nu :

Dans le cas de la lunette afocale , on a :

(4) et (5) :

Le télescope de Newton

L’objectif du télescope est un miroir concave (souvent de forme parabolique).

L'oculaire, comme dans la lunette astronomique, joue le rôle d'une loupe dans l'examen de l’image fournie par l’objectif.

Le faisceau lumineux entrant dans le télescope est réfléchi par l’objectif puis dévié par un petit miroir plan vers l’oculaire.

Modélisation du télescope par un miroir concave sphérique et une lentille mince

(6)

Le miroir sphérique de centre C donne de l’objet AB situé à l’infini (A_¥ B_¥) une image A₁B₁ située dans le plan focal F’₁ de ce miroir.

L’image A₁B₁ devient objet pour le miroir plan qui en donne une image A₂B₂ symétrique par rapport à son plan.

(7)

L’image A₂B₂ devient objet pour l’oculaire qui en donne une image définitive A’B’. Cette image définitive est rejetée à l’infini car l’objet A₂B₂ est dans le plan focal objet F₂ de l’oculaire. Cette position est caractéristique du télescope afocal.

Le grossissement standard

On appelle grossissement d'un télescope est le rapport du diamÈtre apparent de l'image finale au diamÈtre appa­rent de l'objet observé à l'œil nu :

Dans le cas du télescope afocal, on a :

(6) et (7) :