| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
|
|
Soit une onde lumineuse plane, monochromatique, qui tombe sur un paravent P, perpendiculaire à sa direction de propagation. Le paravent est muni avec une ouverture étroite, rectangulaire. La hauteur de cette ouverture a la valeur a. DerriÈre le paravent, à la distance D se trouve un écran E, destiné pour observer la figure de diffraction. Le plan de l'écran est parallÈle avec celui du paravent.
L'ouverture de la fente est beaucoup plus petite que la distance paravent-écran, a<<D, mais dépasse en grandeur la longueur d'onde de la lumiÈre l. DÛ à la trÈs grande valeur de la distance D, les ondes lumineuses secondaires émises par les surfaces élémentaires de la fente peuvent Être considérées comme des ondes planes quand elles arrivent à l'écran.
D'abord on va discuter les ondes secondaires engendrées par une bande de hauteur dz de la fente, placée à la distance z du centre de la fente. Selon le principe d'Huygens-Fresnel, l'amplitude de l'onde secondaire est proportionnelle à l'aire de la surface élémentaire qui l'engendre
![]()
oÙ: - E0 est l'amplitude de l'onde plane qui arrive à la fente
- l est la longueur de la fente
- dz est la hauteur de l'élément de surface
- f est un facteur de proportionnalité dont la valeur peut Être considérée la mÊme pour toutes les ondes secondaires émises au niveau de la fente.
La contribution de cette onde secondaire dans le point M est

On observe que
![]()
Considérant z2 << x2, D2 il résulte

Puisque xz << r02 on peut faire les approximations

Dans ces conditions

Comme résultat de l'interférence des toutes les ondes secondaires dans le point M, on obtient le vecteur lumineux
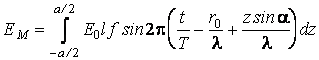
Par l'intégration de la relation on obtient

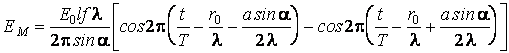

L'intensité lumineuse dans le point M est proportionnelle au carré de l'amplitude du champ électrique

Notant par I0 l'intensité lumineuse dans le point O', on obtient

Il résulte

Parce que

on peut écrire en définitive l'expression de l'intensité lumineuse à la distance x de centre de l'écran

|
|
Sur la représentation graphique du rapport IM/I0, on observe que l'intensité lumineuse est maximum dans le point O'. Au fur et à la mesure que la distance x jusqu'au point O' croit, l'intensité lumineuse varie périodiquement et est caractérisée par la présence de minima et maxima.
Le maximum central est deux fois plus large que les maxima secondaires. La luminosité dans les points de maximum décroit proportionnellement à l'inverse du x2, ce qui permet d'observer seulement un petit nombre de franges d'interférence secondaires.
La figure de diffraction diffÈre beaucoup de celle qui devrait Être observée sur l'écran quand la lumiÈre propagerait en ligne droite et qui consisterait d'une tache de luminosité constante et largeur a.
La position des maxima de luminosité correspond à la condition
![]()
et la position des maxima secondaires correspond à la condition
![]()
L'entrefrange, c'est-à-dire la distance entre deux maxima ou deux minima consécutifs, est
![]()
Il résulte que les franges de diffraction sont parallÈles et équidistantes.
L'analyse théorique sur ce type de diffraction nous permet comprendre plus clairement la signification de l'affirmation 'la diffraction se produit quand la lumiÈre rencontre des obstacles de petites dimensions'. Le problÈme consiste de préciser à quoi s'associe le terme 'petites dimensions'. Pour répondre, on va d'abord observer que la diffraction devient observable quand la largeur du maximum central dépasse la largeur de la fente (ce qui vient en contradiction avec le principe de la propagation rectiligne de la lumiÈre)
![]()
ou
![]()
c'est-à-dire pour observer le phénomÈne de diffraction, la dimension de l'obstacle doit Être inférieure à la moyenne géométrique entre la longueur d'onde et la distance jusqu'au point d'observation. Quand l = 562,5 nm et D = 0,5 m, on a:
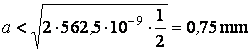
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 911
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved