| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Soit un champ électromagnétique dans le vide. Dans ce cas il n'y a pas de la charge électrique libre ou du courant électrique. Les équations de Maxwell, adaptées pour le vide, ont les formes suivantes

Puisque dans le vide
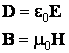
il nous reste

Calculons l'expression ![]() . On
observe qu'il y a deux possibilités
. On
observe qu'il y a deux possibilités
|
|
|
Par la comparaison des résultats, on obtient
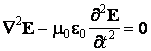
Cette équation est similaire à l'équation de propagation des ondes

correspondant à une vitesse de phase

Procédant de la mÊme maniÈre on peut aussi obtenir l'équation

La conclusion est que dans le vide, une perturbation électrique ou magnétique, produite dans un certain point de l'espace, se propage d'un point à l'autre avec la vitesse de phase c, par l'intermédiaire des champs électriques et magnétiques variables qui s'engendrent réciproquement. Ainsi, est créée une onde électromagnétique.
Soit maintenant une onde électromagnétique plane

On peut démontrer que la solution de cette équation (la fonction d'onde) a la forme
![]()
oÙ
![]()
On va étudier en suite les propriétés de cette solution
Þ selon l'équation

il résulte
![]()
ou
![]()
Puisque l'onde électromagnétique se propage seulement grace aux champs électriques et magnétiques variables, une composante constante ne présente pas d'intérÊt, ainsi qu'on peut choisir
![]()
c'est-à-dire le vecteur l'intensité du champ électrique de l'onde électromagnétique plane est perpendiculaire à la direction de propagation de l'onde.
Pour faciliter les calculs suivants, on va utiliser désormais un systÈme d'axes de coordonnées, ainsi dirigé que le vecteur E soit parallÈle à l'axe Ox
![]()
Þ selon l'équation

il résulte

ou

Par les mÊmes raisons que celles présentées avant, on peut prendre Hx = Hy = 0, ainsi que
![]()
c'est-à-dire le vecteur l'intensité du champ magnétique de l'onde électromagnétique plane est perpendiculaire tant à la direction de propagation de l'onde que au vecteur l'intensité du champ électrique.
|
|
Les trois vecteurs qui caractérisent l'onde électromagnétique c (vitesse de phase), E et H, pris deux par deux sont perpendiculaires, formant un triÈdre droit.
On peut observer que

ou

Alors

Substituant l'expression de la vitesse de phase, on obtient
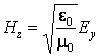
Vu que
![]()
il résulte
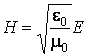
c'est-à-dire l'intensité du champ magnétique et l'intensité du champ électrique d'une onde électromagnétique sont proportionnelles.
La densité d'énergie magnétique de l'onde électromagnétique est égale à la densité d'énergie électrique, comme il résulte du calcul suivant

La densité totale d'énergie de l'onde électromagnétique est
![]()
|
|
Envisageons en suite un élément de volume dV = dxdydz, parcouru par une onde électromagnétique. Notons la densité du courant d'énergie de l'onde par Y. Par définition, la densité du courant d'énergie est l'énergie transportée par l'onde pendant l'unité de temps, à travers l'unité de l'aire normale à la direction de propagation
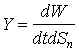
Dans l'élément de volume dV pénÈtre dans l'intervalle de temps dt une quantité d'énergie
![]()
et sort l'énergie
![]()
Le bilan énergétique montre que par suite de ces procÈssus la densité d'énergie de l'élément de volume doit augmenter avec

Par le développement en série et en nous limitant à la premiÈre approximation, il résulte
![]()
Vu que dans le cas de l'onde plane
![]()
on peut réécrire la relation entre la densité d'énergie et la densité du courant d'énergie sous la forme
![]()
Par l'intégration, on obtient
![]()
donc la densité du courant d'énergie de l'onde électromagnétique est proportionnelle à densité d'énergie de l'onde et à sa vitesse de phase.
On peut encore observer que
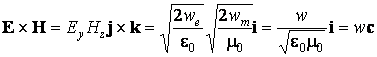
Donc
![]()
La densité du courant d'énergie de l'onde électromagnétique porte aussi le nom de vecteur de Poynting. Le vecteur de Poynting est calculé comme le produit vectoriel entre l'intensité du champ électrique de l'onde électromagnétique et l'intensité de son champ magnétique.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 664
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved