| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
|
|
Le réseau de diffraction est formé par une plaque mince, plane, transparente, sur laquelle est tracé un trÈs grand nombre de raies parallÈles, équidistantes et opaques. Le réseau de diffraction équivaut un nombre N de fentes parallÈles et équidistantes. Le réseau est illuminé avec un faisceau parallÈle de lumiÈre monochromatique, qui tombe sur le réseau à l'incidence normale. Au niveau de chaque fente a lieu la diffraction et les ondes secondaires se dispersent dans toutes les directions.
Les ondes secondaires correspondantes aux rayons de lumiÈre qui font l'angle a avec la direction initiale du faisceau sont concentrées dans le foyer secondaire M d'une lentille convergente L. Dans le point M les ondes secondaires interférent, résultant un certain niveau de luminosité. Les ondes secondaires qui se rencontrent en M parcourent des marches inégales. Si on tient compte que de la source de lumiÈre au réseau de diffraction et du front d'onde AB au point M les rayons parcourent la mÊme marche optique, il résulte que la différence de marche entre le rayon AM (rayon 'zéro') et le rayon au nombre d'ordre k est
![]()
oÙ a est la distance entre deux fentes consécutives, aussi nommée constante du réseau. Dans l'approximation des ondes planes, la contribution d'une onde secondaire dans le point M est

oÙ r0 est la longueur de la marche optique du rayon 'zéro'.
Le résultat de l'interférence est donné par la somme des toutes les contributions des ondes secondaires en M

ou

oÙ ont été faites les notations

Pour calculer la somme on va procéder comme ça:
Þ on observe que
![]()
ainsi que

Þ puisque les termes de la somme constituent une progression géométrique, on va utiliser la formule de sommation des progressions géométriques

Þ comme

il résulte

et

Þ revenant aux notations initiales, on obtient

L'intensité lumineuse dans le point M est proportionnelle au carré de l'amplitude de l'intensité du champ électrique

Le dénominateur de cette expression s'annule si
![]()
ou
![]()
Quand a ak 0 il résulte ![]() et
et ![]() . Comme
. Comme

il résulte
![]()
donc pour les angles ak qui obéissent à la condition ![]() , on obtient des maxima de
diffraction d'intensités égales. Ces maxima de diffraction s'appellent maxima principaux de diffraction. Le
nombre total de maxima principaux de diffraction est limité par la condition
, on obtient des maxima de
diffraction d'intensités égales. Ces maxima de diffraction s'appellent maxima principaux de diffraction. Le
nombre total de maxima principaux de diffraction est limité par la condition
![]()
ou
![]()
Si on prend aussi en considération le maximum d'ordre zéro (pour k = 0), il résulte que le nombre total de maxima principaux qui peuvent Être obtenus avec un réseau est

On peut écrire
|
|
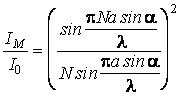
Les minima de diffraction s'obtiennent avec la condition que le numérateur de cette expression s'annule, sans que le dénominateur s'annule aussi. Il résulte
![]()
ou

Donc entre deux maxima principaux de diffraction, on trouve (N - 1) minima nuls.
Enfin, conformément à la condition

ou
![]()
on rencontre les maxima secondaires de diffraction. Leur amplitude décroit au fur et à la mesure que (2k'+1) croit du kN au (kN+N/2), augmentant puis de nouveau quand (2k'+1) s'approche de N(k+1).
L'ouverture angulaire des franges de maximum principales de diffraction est plus grande que celle des maxima secondaires, et leur intensité lumineuse est beaucoup plus forte. Par cela, dans de conditions habituelles, la structure fine des franges de diffraction est peu visible, en se remarquant seulement les franges de maximum principal, séparées par des franges sombres.
La condition remplie à la formation des maxima principaux de diffraction
![]()
peut Être exprimée en fonction de la position des maxima principaux sur l'écran si on observe que

oÙ f est la distance focale de la lentille. Comme

il résulte que la position des maxima principaux correspond à des distances jusqu'au centre de l'écran égales à

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2035
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved