| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
KAUNO TECHNOLOGIJOS UNIVERSITETAS
INŽINERIN S MECHANIKOS KATEDRA
BAIGTINI ELEMENT METODO VADAS
Vienmatis modelis: tampriais ryšiais sujungt masi sistema
/1 NAMU DARBAS/

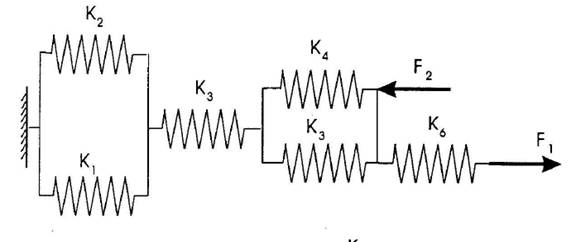
k1=10 N/m;
k2=20 N/m;
k3=30 N/m;
k4=40 N/m;
k6=60 N/m;
F1=100 N;
F2=200 N;
1. Sudaryti vienmat s konstrukcijos baigtini element model
1.1. Pažym ti:
_ Mazginius taškus, j numerius;
_ Baigtini element numerius;
_ Veikian ias apkrovas;
_ Atram reakcijas mazguose.
1.2. Aprašyti baigtini element model
_ Užrašyti element standum matricas;
_ Užrašyti konstrukcijos standumo matric
_ Užrašyti konstrukcijos išorinio poveikio ir reakcijos j g vektorius;
_ Užrašyti konstrukcijos statikos lygt matricine forma, pažymint tvirtintus laisv s
laipsnius.
2. Apskai iuoti:
2.1. Konstrukcijos mazg poslinkius;
2.2. Reakcijos j gas;
2.3. Patikrinkite skai iavimus.
3. Nubraižyti deformuot konstrukcij ir pažym ti reakcijos j gas bei mazg poslinkius.
4. Parašykite program (programinis paketas MATLAB) vienmat s konstrukcijos mazg poslinki ir reakcijos j g , skai iavimui. Palyginkite rezultatus su j s apskai iuotais.
Konstrukcijos baigtiniø elementø modelis:

Elementø standumo matricos
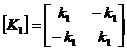
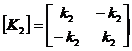

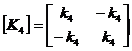
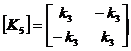

Konstrukcijos standumo matrica
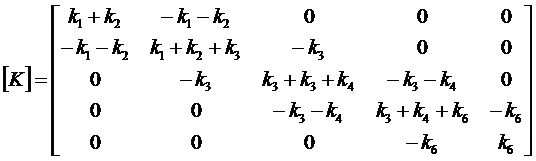
Konstrukcijos išorinio poveikio vektorius:
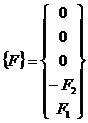
Konstrukcijos reakcijos jëgu vektorius:
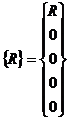
Konstrukcijos statikos lygtis matricine forma ( tvirtinti laisvës laipsniai ávertinami išbraukiant standumo matricos 1eilutæ ir 1stulpelá bei 1 eilutæ poslinkiø, išorinio poveikioir reakcijos jëgø vektoriuose):
![]()
arba


Konstrukcijos mazgø poslinkiø skaièiavimas:
Konstrukcijos statikos lygtis, atmetus átvirtintus laisvës laipsnius

Konstrukcijà aprašo tokia lygèiø sistema:
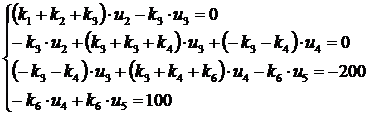
Á šià lygèiø sistemà árašius skaitines standumo reikšmes gauta:
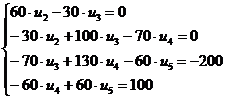
![]()
Iš 1 lygties išsireiškiame u 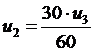
Iš 4 lygties išsireiškiame u ![]()
![]()
Iš 2 lygties išsireiškiame u pries tai i jà ásistate iš 1 lygties išsireikštà u
![]() vietoj u ásistatom
išraiška gautà išsireiškus iš 4 lygties
vietoj u ásistatom
išraiška gautà išsireiškus iš 4 lygties 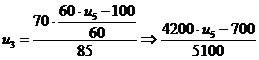
![]()
3 lygtá árašome u ir u išraiškas: ![]()
Iš èia u gauname:
u -6.4286 m
Apskaièiuojame u u3, u
![]()
![]()
![]()
Išsprendæ lygciø sistemà, gavome konstrukcijos mazgø poslinkius:
![]()
![]()
![]()

Kadangi 1 mazgas átvirtintas jo
poslinkis ![]()
Reakcijos jëgø skaièiavimas:
Reakcijos jëgos apskaièiuojamos sudauginus išbrauktà standumo matricos eilutæ su poslinkiø vektoriumi:
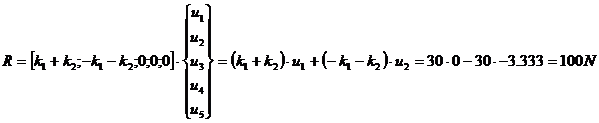
Patikrinimas:
Konstrukcijos statikos lygtis



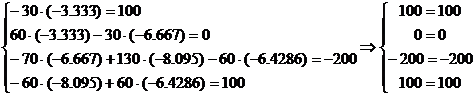
Lygèiø sistema išspresta teisingai.
Deformuota ir nedeformuota konstrukcija
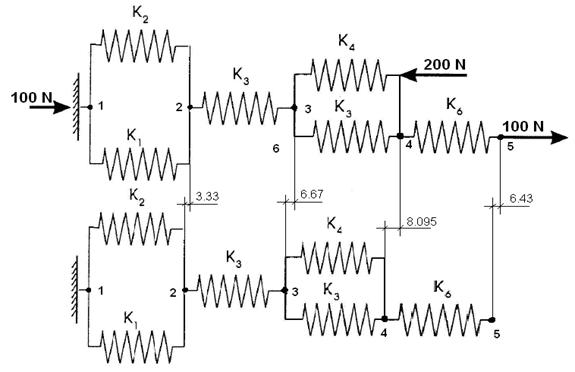
Programa poslinkiams ir reakcijos jëgoms skaièiuoti (Matlab):
% VIENMATES KONSTRUKCIJOS TYRIMAS
clc
clear all
close all
Pradiniu duomenu ivedimas
% Irasykite konstrukcijos elementu standumo reiksmes:
fprintf 'Konstrukcijos elementu standumo reiksmes n'
k1=10
k2=20
k3=30
k4=40
k6=60
% Irasykite konstrukcija veikianciu jegu reiksmes:
fprintf 'Konstrukcija veikiancios jegos n'
F1=100
F2=200
% Irasykite konstrukcijos mazgu skaiciu:
fprintf 'Konstrukcijos mazgu skaicius n'
mazgu_sk=5
% Irasykite itvirtinto mazgo (kuriame u=0) numeri:
fprintf 'Itvirtinto mazgo numeris n'
itvirt_mazgas=1
Konstrukcijos standumo matricos sudarymas
fprintf 'Konstrukcijos standumo matrica'
K = [ k1+k2 -k1-k2 0 0 0
-k1-k2 k1+k2+k3 -k3 0 0
0 -k3 k3+k3+k4 -k3-k4 0
0 0 -k3-k4 k3+k4+k6 -k6
0 0 0 -k6 k6]
Kisbr=K;
% Isorinio poveikio jegu vektorius sudarymas
fprintf 'Isorinio poveikio jegu vektorius F'
F = [ 0
0
0
-F2
F1]
Fisbr=F;
Krastiniu salygu ivertinimas
fprintf 'Konstrukcijos standumo matrica K, ivertinus krastines salygas'
Kisbr(itvirt_mazgas,:)=[];
Kisbr(:,itvirt_mazgas)=[];
Kisbr
fprintf 'Isorinio poveikio jegu vektorius F, ivertinus krastines salygas'
Fisbr(itvirt_mazgas)=[];
Fisbr
Konstrukcijos poslinkiu skaiciavimas
fprintf 'Konstrukcijos poslinkiu vektorius U, ivertinus krastines salygas'
Uisbr = KisbrFisbr
U=zeros(mazgu_sk,1);
for i = 1:itvirt_mazgas-1
U(i,1) = Uisbr(i,1);
end
for i = itvirt_mazgas+1:mazgu_sk
U(i,1) = Uisbr(i-1,1);
end
fprintf 'Konstrukcijos poslinkiu vektorius U'
U
Reakcijos jegu skaiciavimas
isbr_eil=K(itvirt_mazgas,:);
fprintf 'Reakcijos jega'
FR = isbr_eil*U
Patikrinimas
fprintf 'Patikrinimas'
Apkrova = K*U
Rezultatai:
Konstrukcijos elementø standumo reiksmës
k1 = 10
k2 = 20
k3 =30
k4 40
k6 = 60
Konstrukcija veikianèios jëgos
F1 =100
F2 = 200
Konstrukcijos mazgø skaièius
mazgu_sk =5
Itvirtinto mazgo numeris
itvirt_mazgas =1
Konstrukcijos standumo matrica
K =
30 -30 0 0 0
-30 60 -30 0 0
0 -30 100 -70 0
0 0 -70 130 -60
0 0 0 -60 60
Isorinio poveikio jegu vektorius F
F =
0
0
0
-200
100
Konstrukcijos standumo matrica K, ivertinus krastines salygas
Kisbr =
60 -30 0 0
-30 100 -70 0
0 -70 130 -60
0 0 -60 60
Isorinio poveikio jegu vektorius F, ivertinus krastines salygas
Fisbr =
0
0
-200
100
Konstrukcijos poslinkiu vektorius U, ivertinus krastines salygas
Uisbr =
-3.3333
-6.6667
-8.0952
-6.4286
Konstrukcijos poslinkiu vektorius U
U =
0
-3.3333
-6.6667
-8.0952
-6.4286
Reakcijos jega
FR 100.0000
Patikrinimas
Apkrova =
100.0000
0.0000
0
-200.0000
100.0000
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1481
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved