CATEGORII DOCUMENTE
Afaceri Calculatoare Casa masina Didactica pedagogie Diverse Educatie Finante Geografie Istorie & politica Legislatie Limba Management Sanatate Tehnologie

Bulgara	Ceha slovaca	Croata	Engleza	Estona	Finlandeza	Franceza
Germana	Italiana	Letona	Lituaniana	Maghiara	Olandeza	Poloneza
Sarba	Slovena	Spaniola	Suedeza	Turca	Ucraineana

įstatymai	įvairių	Apskaitos	Architektūra	Biografija	Biologija	Botanika	Chemija
Ekologija	Ekonomika	Elektra	Finansai	Fizinis	Geografija	Istorija	Karjeros
Kompiuteriai	Kultūra	Literatūra	Matematika	Medicina	Politika	Prekyba	Psichologija
Receptus	Sociologija	Technika	Teisė	Turizmas	Valdymas	vietimas

Dielektrikai elektriniame lauke (orientacine poliarizacija, joninė poliarizacija)

elektra

+ Font mai mare | - Font mai mic


DOCUMENTE SIMILARE

Dielektrikai elektriniame lauke (orientacine poliarizacija, joninė poliarizacija)?

Dielektrikų poliarizacija

Vienalyčiame dielektrike iskirkime makroskopinį tūrį ∆V, kuriame molekulių skaičius N> 1. Iskirtosios med˛iagos elektrinis dipolinis momentas lygus visų jo molekulių elektrinių dipolinių momentų geometrinei su Jos tūrio vieneto dipolinis momentas

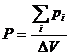(2.1)

Dielektrikas vadinamas poliarizuotu, kai P≠O. Taigi is dydis yra poliarizacijos kiekybinis matas ir vadinamas dielektriko poliarizuotumu, arba poliarizacijos vektoriumi. Poliarizuotumo SI vienetas yra kulonas kvadratiniam metrui (C/m²). Aptarkime, nuo ko priklauso nepolinių bei polinių dielektrikų poliarizuotumas.

Orientacinė poliarizacija, Nagrinėkime izotropinį ir vienalytį polinį dielektriką, t. y. tokį, kurio elektrinės savybės nepriklauso nuo lauko krypties ir visuose takuose yra vienodos. Jame iskirkime makroskopinį tūrį ∆V, kuriame telpančių molekulių skaičius N>1. Dėl molekulių iluminio judėjimo jų elektriniai dipoliniai momentai yra įvairiausios orientacijos, kuri, be to, nuolatos kinta. Todėl dielektriko tūrio vieneto dipolinių momentų geometrinė suma lygi nuliui — dielektrikas nepoliarizuotas. Elektrinio lauko veikiamos polinės molekulės įgyja potencinę energiją W_p. Jeigu molekulės chaotikai nejudėtų (T=0K), tai visos jos elektriniame lauke orientuotųsi palankiausiai energijos po˛iūriu (p || E). Tačiau dėl iluminio judėjimo, esant termodinaminei pusiausvyrai (T=const), dalelės pagal potencinės energijos vertes pasiskirsto Bolcmano dėsniu (˛r. lt., 12.5 sk.):

(2.9)

Kaip matyti (2.9) formulėje, kuo didesnį kampą - sudaro vektorius p su vektoriumi E (didesnė energija W_p), tuo tokių molekulių koncentracija n () yra ma˛esnė. Taigi, nekintant lauko stiprumui ir temperatūrai, nusistovi elektrinių dipolinių momentų dalinė orientacija — dielektrikas pasidaro poliarizuotas (P≠O). Dielektriko poliarizacija, kuri atsiranda laukui orientuojant dipolių elektrinius momentus, vadinama orientacine.

Atskirą dielektrikų grupę sudaro joniniai kristalai (NaCl, KC1 ir kt.). Elektrinio lauko veikiama, teigiamų jonų subgardelė pasislenka iilgai vektoriaus E krypties, o neigiamų jonų subgardelė — prieinga kryptimi, ir kristalas įgyja elektrinį dipolinį momentą. itokia poliarizacija vadinama jonine. Ji yra deformacinės poliarizacijos rūis.

Maksvelio lygtys: elektrinės slinkties vektorius, slinkties srovė?

Slinkties srovė.Kaip matėme 5.1 skirsnyje, kiekviena laidumo ar konvekcinė elektros srovė kuria magnetinį lauką. is reikinys yra svarbiausias elektros srovės po˛ymis. Tačiau 1861 m., apibendrindamas kitų fizikų eksperimentus, D˛. Maksvelis atrado fundamentalų gamtos dėsnį, kuris teigia, kad kiekvienas kintamasis magnetinis laukas erdvėje kuria sūkurinį elektrinį lauką ir kiekvienas kintamasis elektrinis laukas kuria sūkurinį magnetinį lauką. Taigi kintamasis elektrinis laukas magnetinio lauko kūrimo aspektu yra ekvivalentus elektros srovei, todėl D˛. Maksvelis jį pavadino slinkties srove. Raskime kintamojo elektrinio lauko ir jo sukurto magnetinio lauko kiekybinį ryį. Tam nagrinėkime kintamosios srovės grandinę, į kurią įjungtas kondensatorius su idealiai nelaid˛iu dielektriku (8.5 pav.). Tekant kintamajai srovei, kondensatorius periodikai įsikrauna ir isikrauna. Dėl to tarp jo elektrodų elektrinis laukas kinta laike ir, pagal D˛. Maks-velį, pro kondensatorių teka magnetinį lauką kurianti slinkties srovė. Jei kondensatoriaus krūvis q, vieno elektrodo paviriaus plotas S_o, tai elektrodu tekančios laidumo srovės tankis

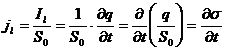
čia dydis σ = q/S₀ yra kondensatoriaus elektrodo krūvio pavirinis tankis. Tarsime, kad kondensatoriaus elektrodai — didelės lygiagrečios ploktumos

ir yra slinkties srovės tankio modulis.

Taigi, kintant elektriniam laukui (D), tiek vakuume, tiek dielektrike „teka' slinkties srovė, kurianti magnetinį lauką visai taip pat kaip ir laidumo srovė. Pagal (2.23), elektrinė slinktis dielektrike u˛raoma itaip:

D = ε₀E + P;

čia E — elektrinio lauko stiprumas vakuume, P — dielektriko poliarizuo-tumas. Todėl slinkties srovės tankis dielektrike susideda i dviejų dėmenų:

Pirmasis dėmuo nusako slinkties srovės tankį vakuume. Jis susijęs tik su elektrinio lauko kitimu laike. Jeigu ivestinė , tai su itokiu elektriniu lauku visuomet susijęs sūkurinis magnetinis laukas. Toji slinkties srovės dedamoji visai nesusijusi su krūvininkų judėjimu ar ilumos iskyrimu. Visai kitaip yra su antrąja dedamąja .Ji reikia tankį srovės, kurią sudaro suritųjų elektros krūvių tvarkingas judėjimas dielektrike (krūvių pasislinkimas molekulėje arba elektrinių dipolių pasisukimas). Tokia srovė vadinama poliarizacijos srove, ir dėl jos isiskiria D˛aulio iluma. Taigi i slinkties srovės dedančioji i esmės yra tokios pat prigimties kaip laidumo srovė.

Maksvelio lygtys: pilnutinės srovė?

Pilnutinė srovė. Slinkties srovė „teka' visur, kur kinta elektrinis laukas: vakuume, dielektrike, laiduose. Todėl bendru atveju laidumo, konvekcinės ir slinkties srovės nebūna atsiskyrusios erdvėje: visos jos gali egzistuoti kartu tame pačiame tūryje ir galima kalbėti apie pilnutinę srovę bei jos tankį. Pilnutinės srovės tankis u˛raomas itaip:

Tačiau laiduose slinkties srovės tankis, palyginti su laidumo srovės tankiu, yra nykstamai ma˛as, ir jo da˛niausiai nepaisoma. Pilnutinė srovė pro bet kokį, u˛dara kreive l ribojamą, ploto S pavirių apskaičiuojama pagal formulę:

čia yra laidumo srovė, - slinkties srovė.

Įvedus pilnutinės srovės sąvoką, imta naujai traktuoti elektros srovės grandinių u˛darumą. Iki tol buvo manoma, kad kintamosios srovės elektros grandinė gali būti neu˛dara. Pagal Maksvelį, kaip ir nuolatinės srovės, kintamosios srovės grandinės yra u˛daros ir bet kuriame jų skerspjūvyje kvazistacionariosios pilnutinės srovės stiprumas tuo pačiu laiko momentu yra vienodas. Tokias grandines „u˛daro' slinkties srovės, „tekančios' tomis grandinės dalimis, kur nėra laidininkų, pavyzd˛iui, tarp kondensatoriaus elektrodu.

iluminis spinduliavimas. Absorbcinė geba?

Tačiau kvantinei optikai ir apskritai kvantinei fizikai sukurti bene daugiausia duomenų gauta nagrinėjant iluminį spinduliavimą. Čia tenka pabrė˛ti, kad spinduliavimo (radiacijos) sąvoką fizikai vartoja dviem prasmėmis: 1) ji reikia vakuume ar materialioje erdvėje sklindančių elektromagnetinių bangų ar dalelių srautą; 2) bangų ar dalelių sklidimo i materialiosios sistemos procesą. Gamtoje labiausiai paplitęs spinduliavimas, kurį su˛adina med˛iagos dalelių iluminiai virpesiai. itaip sukeltas elektromagnetinis spinduliavimas vadinamas iluminiu, arba temperatūriniu. Kiekvienas kūnas, kurio temperatūra auktesnė kaip 0 K, spinduliuoja energiją. Tačiau būdamas ˛emos temperatūros, jis skleid˛ia tik infraraudonuosius spindulius; kuo temperatūra auktesnė, tuo platesnis spinduliavimo da˛nių diapazonas: auktoje temperatūroje jau spinduliuojami regimieji bei ultravioletiniai spinduliai. Be to, kylant temperatūrai, didėja bet kokio da˛nio spinduliavimo intensyvumas. Taigi iluminio spinduliavimo intensyvumas ir spektras priklauso nuo spinduliuojančio kūno savybių ir temperatūros.

Spinduliuojantį kūną A (1.1 pav.) apgaubkime spinduliavimą idealiai atspindinčiu apvalkalu. Tuomet kūno skleid˛iamoji spinduliavimo energija neisisklaido erdvėje, o visikai atsispindėjusi nuo apvalkalo vėl daugiau ar ma˛iau sugeriama kūno — vyksta nepertraukiama energijos kaita. Kai per laiko vienetą kūnas ispinduliuoja tiek pat energijos, kiek ir sugeria, tarp kūno ir jo spinduliavimo nusistovi dinaminė pusiausvyra. itokį kūno iluminį spinduliavimą vadiname pusiausviruoju. Patirtis rodo, kad tik iluminis spinduliavimas gali būti pusiausvirasis. Visų rūių liuminescencinis spinduliavimas yra nepusiausvirasis.

Spektrinis spinduliavimo tankis. Kietųjų kūnų ir skysčių iluminio spinduliavimo spektras yra itisinis: jį sudaro platesnis ar siauresnis da˛nių ν (arba bangos ilgių λ) intervalas. Pa˛ymėkime dW_W: _T energijos srautą (energijos kiekį, ispinduliuotą per laiko vienetą), kurį vienetinio ploto kūno pavirius spinduliuoja 2n erdviniu kampu da˛nių intervale nuo ν iki ν + dν. Jei intervalo plotis dν labai ma˛as, tai dW_ν, _T~dν, o jų santykis

vadinamas spektriniu energijos spinduliavimo tankiu arba emisijos geba (labiau paplitęs terminas). i svarbiausia kiekybinė kūno iluminio spinduliavimo charakteristika ireikia sąryį tarp temperatūros Z'ir spinduliavimo pasiskirstymo pagal da˛nį ν. Be abejo, is dydis ireikia ir spinduliavimo energijos pasiskirstymą pagal bangos ilgį:

čia dλ — bangos ilgių intervalas, atitinkantis da˛nių intervalą dν. Suintegravę (1.1.1) bei (1.1.2) lygybes atitinkamai visų galimų da˛nio ar bangos ilgio verčių at˛vilgiu, gautume visą spinduliuojamo energijos srauto tankį, kuris priklauso tik, nuo temperatūros.

Absorbcijos geba. Sakykime, į kūno paviriaus elementarųjį plotelį krinta da˛nių intervalo nuo ν iki ν+dν spinduliavimo energijos srautas dW_v,T. io srauto dalį dW'_v,T kūnas sugeria. Nedimensinį jų santyki:

vadiname kūno absorbcijos geba. is dydis priklauso nuo nagrinėjamojo kūno temperatūros ir krintančio spinduliavimo da˛nio arba bangos ilgio. Kūną, kurio bet kokioje temperatūroje visų da˛nių spinduliavimo absorbcijos geba A_ν,T=l, G. Kirchhofas pavadino absoliučiai juodu kūnu. Jis sugeria visus į jį kritusius spindulius. ia savybe gamtoje jam artimiausi yra suod˛iai. Gana plačioje spektro srityje jų absorbcijos geba artima 0,99, tačiau ˛emų da˛nių infraraudonoje spektro srityje ji yra gerokai ma˛esnė.

Galima pagaminti kūną, kurio spinduliavimo ir absorbcijos savybės labai artimos absoliučiai juodo kūno savybėms.

Absoliučiai juodo kūno spinduliavimo dėsniai?

Absoliučiai juodo kūno spinduliavimo empiriniai dėsniai,

Da˛nai reikia ˛inoti, kiek energijos spinduliuoja per 1 s kūno paviriaus ploto vienetas 2π erdviniu kampu visais da˛niais nuo 0 iki ∞ is nuo kūno temperatūros T priklausantis dydis W_T vadinamas energiniu viesiu, arba ispind˛iu jis ireikiamas itaip:

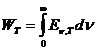
1879 m. austrų fizikas J. Stefanas, eksperimentikai tirdamas kūnų pusiausvirąjį iluminį spinduliavimą, nustatė, kad jų energinis viesis yra tiesiog proporcingas absoliutinės temperatūros T ketvirtajam laipsniui. Vėliau eksperimentikai nustatyta, kad is teiginys tikrai teisingas tik absoliučiai juodam kūnui. Remdamasis termodinamika, tokią pat ivadą 1884 m. gavo kitas austrų fizikas L. Bolcmanas. Todėl is absoliučiai juodo kūno iluminio spinduliavimo dėsningumas vadinamas Stefano ir Bolcmano dėsniu. Jis u˛raomas itaip:.

Proporcingumo koeficientas σ yra fundamentali fizikinė konstanta, vadinama Stefano ir Bolcmano konstanta. Eksperimentais nustatyta, kad σ = 5,67032 • 10 ^-8 W/(m² • K⁴).

Difrakcine gardele ar kitokiu spektro analizatoriumi suskaid˛ius absoliučiai juodo kūno skleid˛iamus spindulius į spektrą, eksperimentikai nustatomos spinduliavimo spektrinio

tankio ε_v, _T arba ε_λ, _T vertės 1.4 pav.

E_λ,T

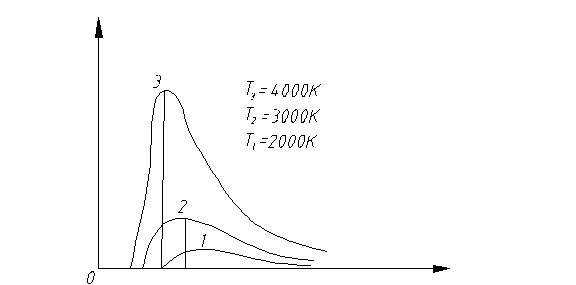
paveiksle parodytos dyd˛io e_λ, _Tpriklausomybės nuo λ kreivės, esant konkrečioms temperatūros vertėms. I jų galima padaryti itokias ivadas.

Absoliučiai juodo kūno spinduliavimo spektras yra itisinis, t. y. spinduliuojamos įvairaus da˛nio (ilgio) bangos.

2. Tam tikrą bangos ilgį λ_o atitinka spektrinio spinduliavimo tankio maksimumas. Kylant temperatūrai T, is maksimumas slenka link trumpųjų bangų. 1893 m. vokiečių fizikas V. Vynas nustatė tokį dyd˛ių λ_o ir T sąryį: absoliučiai juodo kūno spektrinio spinduliavimo energijos tankio maksimumą atitinkantis bangos ilgis yra atvirkčiai proporcingas kūno temperatūrai, t.y.

čia b — vadinamoji Vyno konstanta; nustatyta, kad b = 0,002898 m • K. (1.2.3) sąryis vadinamas Vyno poslinkio dėsniu. I jo iplaukia, kad absoliučiai juodo kūno spinduliavimo maksimumas 6000 K temperatūroje yra regimojoje spektro srityje. Kai temperatūra ˛emesnė, is maksimumas esti ilgesnių bangų srityje. Todėl vytinčiam kūnui vėstant, jo spektre ima vyrauti vis ma˛esnio da˛nio viesa, iki galų gale kūnas visai nustoja skleisti regimuosius spindulius.

Planko hipotezė ir formulė?

Spinduliavimo kvantinė hipotezė ir Planko dėsnis

1.4 paveiksle parodytų kreivių teorinis nagrinėjimas turėjo lemiamos reikmės fizikos mokslo raidai. Tiriant absoliučiai juodo kūno spinduliavimą, to kūno teoriniu modeliu imama visais galimais da˛niais virpančių harmoninių osciliatorių¹ begalinė sistema. Pagal klasikinę elektrodinamiką kiekvienas toks osciliatorius spinduliuoja jo virpesių da˛nio elektromagnetines bangas. Be to, pagal ią teoriją kiekvienos sistemos energija gali kisti tolyd˛iai, t. y. sistema gali ispinduliuoti bet kokias energijos vertes. Laikantis ios elektromagnetinio spinduliavimo koncepcijos, nepavyko teorikai gauti 1.4 paveiksle parodytų kreivių analizinės iraikos. Vadinasi, minėtoji iluminio spinduliavimo koncepcija neatitinka tikrovės. 1900 m. vokiečių fizikas M. Plankas paskelbė klasikinei fizikai prietaraujančią prielaidą: da˛niu ν virpančio osciliatoriaus energija W gali būti ne bet kokia, o tik dyd˛io hν kartotinė, t. y.

W = nhν; n=1, 2, 3,.; (1.4.1)

čia h —Planko konstanta. Eksperimentikai nustatyta, kad J^.s. Dydį, kurio dimensija ireikiama sandauga

energija laikas,

fizikai vadina veikimu. Dėl to Planko konstanta dar vadinama veikimo kvantu. Taigi pagal Planko hipotezę osciliatoriaus energija gali būti ne bet kokia - ji kvantuota. Dydis.

ε = hv

yra ma˛iausias galimas osciliatoriaus energijos kiekis; jis vadinamas energijos 'kvantu. Remdamasis ia energijos kvantavimo hipoteze ir statistinės fizikos dėsniais, M. Plankas gavo itokią absoliučiai juodo kūno spinduliavimo spektrinio tankio analizinę iraiką:

(1.4.3)

čia k — Bolcmano konstanta, c — viesos greitis vakuume. i Planko formulė aprao energijos pasiskirstymą absoliučiai juodo kūno spinduliavimo spektre.

I (1.1.1) ir (1.1.2) lygybių gauname: - Čia minuso ˛enklas įraytas todėl, kad pokyčiai dν ir dλ yra prieingų ˛enklų. I lygybės ν = c/λ ivestinė dν/dλ= - c/λ², todėl Į pastarąją lygybę įraę (1.4.3) iraiką ir i lygybės c = λν spinduliavimo da˛ni ν pakeitę bangos ilgiu λ, gauname itokią iraiką:

(1.4.4)

Pagal ią formulę apskaičiuotos dyd˛io teorinės vertės labai gerai sutampa su 1.4 paveiksle parodytomis eksperimentinėmis. Tai patvirtina energijos kvantavimo Planko hipotezę.

(1.4.3) ar (1.4.4) lygybes suintegravus visų da˛nių ν ar bangų ilgių λ diapazone, gaunamas Stefano ir Bolcmano dėsnis.

Kai temperatūra pastovi, funkcijos (1.4.4) ekstremumo sąlyga yra . I jos iplaukia Vyno poslinkio dėsnis (1.2.3). Taigi empiriniai absoliučiai juodo kūno iluminio spinduliavimo dėsniai iplaukia i M. Planko ivestos formulės.

Fotonai jų charakteristika ?

Fotono masė, sklidimo greitis c ir judesio kiekis

Visi fotoefekto dėsningumai paaikinami spinduliavimo fotonine struktūra. Susipa˛inkime su kitomis svarbiausiomis fotono korpuskulinėmis charakteristikomis: mase, sklidimo greičiu ir judesio kiekiu. Fotono energija ireikiama lygybe ε = hν. Taikant Einteino masės ir energijos sąryio dėsnį, fotono masė ireikiama itaip:

(1.6.1)

Dalelės, judančios viesos greičiui vakuume c artimu greičiu v, vadinamos reliatyvistinėmis. Jų masė ireikiama lygybe

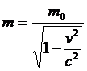
kurioje m₀ — dalelės rimties masė. I čia iplaukia, kad viesos greičiu c judančios dalelės rimties masė m_o = 0. Pavyzd˛iui, taikykime vakuume judančiam fotonui (v = c). Jeigu fotono rimties masė (m₀) būtų nelygi 0, tai i formulės gautume m=∞. Tokia ivada prietarauja tikrovei; vadinasi, fotono rimties masė m_o = 0, t. y. rimties būsenos fotonai neegzistuoja. Iplaukia ir kita svarbi ivada: fotonas ir med˛iągoję juda greičiu c.

Prieingu atveju, jeigu fotono greitis med˛iagoje būtų v < c, ir gautume m = 0. Fotonas, kuris neturi masės, neturi ir energijos, t. y. jis i viso neegzistuoja. Į (1.6.2) įraę fotono rimties masės vertę m_o ir greitį v=c, fotono masę gauname neapibrė˛tą: m=0/0. Nors i ios lygybės fotono masės apskaičiuoti negalime, tačiau pats neapibrė˛tumas neprietarauja fotono buvimui.

Eksperimentikai nustatytą faktą, kad viesos greitis med˛iagoje ma˛esnis negu vakuume, paaikiname itaip: med˛iagoje greičiu c sklindantis fotonas retkarčiais sugeriamas ir vėl ispinduliuojamas. Dėl to l ilgio kelią med˛iagoje jis sklinda ilgesnį laiko tarpą t negu vakuume, ir viesos greitis, apskaičiuotas i lygybės v = lt, yra ma˛esnis u˛ c.

Fotonas, kaip ir kiekviena dalelė, apibūdinamas judesio kiekiu

ios lygybės skaitiklį ir vardiklį padaliję i 2π gauname:

čia įraytas dydis vadinamas ma˛ąja Planko konstanta, k = 2π/λ - bangos skaičiumi. Vektorius k, kurio modulis lygus bangos skaičiui, o kryptis sutampa su bangos sklidimo kryptimi, vadinamas bangos vektoriumi. Vektoriai p ir k yra kolinearūs, todėl lygybė vektorikai u˛raoma itaip:

p=ћk.

Heizenbergo neapbrė˛tumų sąryiai?

Klasikinėje mechanikoje dalelės pradinė būsena tiksliai apibudinama jos masės centro trimis erdvinėmis koordinatėmis ir tuo pat metu tiksliai apibrė˛tomis trimis judesio kiekio projekcijomis p_x, p_y, p_z. Jeigu ˛inomas dalelės judėjimo dėsnis, tuomet visi ie ei dyd˛iai tiksliai ˛inomi ir bet kuriuo kitu laiko momentu. I čia ir iplaukia ivada, kad klasikinei dalelei būdinga apibrė˛ta judėjimo trajektorija, t. y. jos koordinačių verčių kaitos seka bėgant laikui.

Kadangi mikrodalelės i esmės skiriasi nuo makrokūnų, tai ios sąvokos jų būsenai aprayti netinka. Čia turėtų būti vartojami mikropasauliui būdingi dyd˛iai ir sąvokos. Tačiau bet kokią informaciją apie mikrodalelę gauname bandymo metu i jos sąveikos su makroskopinių matavimo įrenginiu. Taigi matavimo rezultatus turime ireikti makroskopines būsenas apraančiais dyd˛iais, t. y. dinaminiais kintamaisiais.

(2.3.1)

∆p_x∆x≈pλ. = h.

Pastaroji apytikslė lygybė vadinama Heizenbergo neapibrė˛tumo lygtimi. Atsi˛velgus į auktesnės eilės difrakcinius maksimumus, dydis ∆p_x gaunamas didesnis negu pagal (2.3.1) formulę, todėl bendriau nagrinėjant (2.3.2) lygtis pavirsta itokia nelygybe:

∆p_x∆x≥h

Pagal ją vienu ir tuo pačiu metu mikrodalelės koordinatės ir atitinkamos judesio kiekio projekcijos neapibrė˛tumų sandauga yra ne ma˛esnė u˛ h. i nelygybė vadinama Heizenbergo neapibrė˛tumo sąryiu¹ arba tiesiog — Heizenbergo nelygybe. Ji ireikia fundamentalų kvantinės mechanikos principą, teigiantį, kad mikrodalelių būsenų, kurias tiksliai apibūdina judesio kiekis, tuo pačiu laiko momentu neįmanoma tiksliai apibūdinti koordinatėmis ir atvirkčiai.

Analogika (2.3.3) tipo nelygybę galima parayti dyd˛ių y ir p_y, z ir p_z arba dar kai kurių kitų dyd˛ių poroms. Tokios dyd˛ių poros fizikoje vadinamos kanonikai jungtiniais dyd˛iais. Bėjau minėtų kanonikai jungtinių dyd˛ių, fizikoje labai svarbi dar viena jų pora — dalelės energija W ir laikas t. iems dyd˛iams Heizenbergo nelygybė u˛raoma itaip:

(2.3.4)

I io sąryio galima daryti ivadą, kad dalelės energijos nustatymas tikslumu ∆W visuomet u˛trunka laiko tarpą, ne ma˛esnį kaip τ ≈ j/ ∆ W. I io sąryio taip pat iplaukia, kad su˛adintų molekulių, atomų bei jų branduolių energija nėra grie˛tai apibrė˛ta, o pasi˛ymi tam tikru verčių intervalu ∆W. Jis vadinamas su˛adintojo lygmens natūraliuoju pločiu. Jeigu su˛adintos būsenos gyvavimo vidutinė trukmė yra τ tuomet jos energijos neapibrė˛tumas yra ne ma˛esnis kaip ∆W≈h τ

Kadangi Heizenbergo nelygybė yra fundamentali, tai ji turi tikti bet kokios fizikinės sistemos, taigi ir makroskopinės, kanonikai jungtiniams dyd˛iams. Tačiau kadangi Planko konstanta yra labai ma˛a, tai makroskopinės sistemos abiejų dyd˛ių neapibrė˛tumai vienu metu yra labai ma˛i, t. y. patys dyd˛iai pakankamai tikslūs. itai ir teigia klasikinė mechanika. Su mikrodalelėmis yra kitaip. Tačiau tam tikruose u˛daviniuose ir joms vienu metu abiejų dyd˛ių neapibrė˛tumai praktikai gali būti pakankamai ma˛i. Tokiais atvejais mikrodalelėms taip pat taikytina klasikinė fizika. Minėtas ivadas iliustruokime pavyzd˛iais

1. Sakykime, iilgai aies Ox greičiu v_x.= 10⁶ m/s juda elektronas. Tarkime, kad jo greitis nusakytas gana dideliu tikslumu, pavyzd˛iui, 0,01 %. Įvertinkime maksimalų tikslumą, kuriuo galima nustatyti elektrono koordinatę. Tam i (2.3.3) nelygybės ireikiame koordinatės neapibrė˛tumą:

∆ x ≥h/∆p_x, arba ∆x> h / (m ∆ v_x).

I duotųjų sąlygų (100∆v_x/v_x= 0,01) apskaičiuojame greičio neapibrė˛tumą ∆v_x≈1O² m/s. Į (2.3.5) nelygybę suraę įeinančių dyd˛ių skaitines vertes, gauname:

∆x≥7^.10^-6m.

Kaip matome, iuo atveju elektrono koordinatę galima nustatyti praktikai gana dideliu (~7 µm) tikslumu. Taigi iuo atveju elektrono koordinatė ir judesio kiekis vienu metu yra gana tiksliai nusakomi, todėl elektroną tam tikru artutinumu galima laikyti klasikine dalele, kalbėti apie jo judėjimą linijine trajektorija, t. y. jam taikyti klasikinę mechaniką.

2. Dabar nagrinėkime elektrono judėjimą nesu˛adinto vandenilio atome. I Boro elementariosios teorijos iplaukia, kad ioje būsenoje elektrono greičio modulis v≈2,2^.10⁶ m/s. iuo atveju elektrono koordinatės nustatymo tikslumas prilygsta atomo tiesiniams matmenims, t. y. ∆x 10^-10 m. I (2.3.5) nelygybės, įvertinę greičio neapibrė˛tumą, gauname, kad ∆v ≥ 7 • 10⁶ m/s. Čia jau yra kitaip negu pirmuoju atveju: koordinatės neapibrė˛tumas ma˛as, u˛tat greičio — didesnis u˛ patį greitį. iuo atveju elektrono negalima laikyti ma˛a dalele, negalime kalbėti apie jo linijinę orbitą, t. y. jam būtina taikyti kvantinę mechaniką.

3. Heizenbergo nelygybę pritaikykime 10^-18 kg masės makroskopinei dulkelei. Sakykime, jos koordinatė nustatoma 1 µm tikslumu. I minėtos nelygybės gaunamas apie 10^-9 m/s greičio neapibrė˛tumas. is dydis yra ˛ymiai ma˛esnis u˛ iuo metu pasiektą did˛iausią greičio matavimo tikslumą. Taigi makroskopinė dulkelė, kaip ir kiekvienas kitas makroskopinis kūnas, yra klasikinės fizikos tyrimo objektas, apraomas jos sąvokomis.

Reikia pabrė˛ti, kad i Heizenbergo nelygybės įvertinama tik vieno ar kito kanonikai jungtinio dyd˛io neapibrė˛tumo didumo eilė. Todėl autoriai, iskirtinai besinaudojantys ma˛ąja Planko konstanta ћ = h/2π, ir Heizenbergo nelygybėje vietoj h rao ћ.

rėdingerio lygtis?

Bendroji rėdingerio lygtis. Kaip ˛inome, fundamentalūs gamtos dėsniai ir juos ireikiančios lygtys u˛raomos remiantis postulatais. Isprendę svarbiausią kvantinės mechanikos lygtį, gauname dalelės ar dalelių sistemos būseną apraančią banginę funkciją. Tai, kad sprendimo rezultatas yra funkcija, o ne skaičius, rodo, jog i lygtis turi būti diferencialinė. Ją 1926 m. postulavo austrų fizikas E. rėdingeris, todėl ji dabar vadinama

bendrąja rėdingerio lygtimi¹. Ji u˛raoma itaip:

(2.6.1)

čia i — menamasis vienetas, o - Hamiltono operatorius, Ψ – banginė funkcija. Bendrąją rėdingerio lygtį perraome itaip:

(2.6.2)

čia ∆ — Laplaso operatorius. Dydis V yra tokia koordinačių ir laiko funkcija, kurios neigiamas gradientas lygus jėgai, kuri veikia m masės dalelę. Tuo atveju, kai dydis V nuo laiko tiesiogiai nepriklauso, jis reikia daleles potencinę energiją. Taigi rėdingerio lygtis yra postuluota antrosios eilės diferencialinė lygtis. Isprendus ią lygtį gauti teoriniai rezultatai gerai sutampa su eksperimentiniais duomenimis, taigi patvirtina kvantinės mechanikos postulatus. Kitame skirsnyje isprendę rėdingerio lygti, t. y. padarę atvirkčiai negu E. rėdingeris, gausime jo postuluotąją laisvosios, dalelės de Broilio bangos matematinę iraiką.

Boro atotykio principas?

Energijų, atitinkančių gretimas kvantinio skaičiaus n vertes, skirtumas

(2.8.7)

Įvertinkime į skirtumą skirtingos masės dalelėms, esančioms įvairaus pločio potencialo duobėje, kai dalelės būsenos kvantinis skaičius n≥1. Sakykime, dalelės masė m yra molekulės masės didumo eilės, t. y. apie 10 ^-26 kg, o duobės plotis apie 10 cm (pvz., molekulė vienmačiame inde). Tuomet pagal (2.8.7) gauname, kad ∆W≈10^-39,n J. itokio ma˛o energijų skirtumo neįmanoma u˛fiksuoti jokiais bandymais. Analogiką rezultatą gautume elektronui (m ≈10 ^-30 kg), judančiam tokio pat didumo potencialo duobėje (pvz., laisvasis elektronas metale). Čia ∆W_n≈10^-35 ^,n J. Taigi nors dalelės energija čia yra kvantuota, jos diskretikumo bandymai nerodo. Todėl čia pagrįstai galima laikytis klasikinės fizikos po˛iūrio, kad dalelės energijos spektras itisinis, ir jos judėjimui taikyti klasikinę fiziką.

Visai kitaip gauname elektronui, esančiam atomo matmenų eilės (l≈10^-10m) potencialo duobėje. iuo atveju ∆W_n≈10^-17.n J= 10² ^.n eV energijos diskretikumas gana rykus ir kvantiniai reikiniai lengvai pastebimi. Tačiau mikrodalelėms kvantiniai reikiniai būdingi tik tuomet, kai juos nusakantys veikimo dimensijos (energijos laiko) dyd˛iai yra Planko konstantos h didumo eilės. Tuomet jiems būtina taikyti kvantinę mechaniką. Prieingu atveju, kai ie dyd˛iai labai dideli h at˛vilgiu, ių dalelių kvantinės savybės eksperimentikai nepastebimos ir joms pakankamai gerai tinka nesudėtinga klasikinė fizika. Pavyzd˛iui

kai n vertės labai didelės, artėja prie 0. Tuo atveju energijos diskretumo galima nepaisyti. 1923 m. N. Boras suformulavo tokį postulatą: didelių kvantinių skaičių atveju kvantinės fizikos ivados sutampa su klasikinės fizikos ivadomis. is teiginys dar vadinamas Boro atotykio principu.

Elektronų būsenų kvantiniai skaičiai?

į bandymą 1925 m. iaikino JAV fizikai S. Gaudsmitas ir D˛. Ulenbekas. Jie padarė prielaidą, kad elektronas pasi˛ymi savuoju judesio kiekio momentu, trumpai vadinamu sukiniu arba spinu. Su juo susijęs savasis magnetinis momentas

p_ms. Eksperimentikai nustatyta, kad pastarojo vektoriaus projekcija iilgai B nukreiptoje Oz ayje skaitine verte lygi Boro magnetonui, t. y.

(2.14.2)

Pagal jų pasiūlytą sukinio modelį elektronas yra įelektrintas rutuliukas, kaip vilkelis besisukantis apie tam tikrą aį. Tačiau tokio sukinio samprata prietarauja reliatyvumo teorijai. Kad taip besisukantis elektronas įgytų eksperimentikai nustatytą (2.14.2) p_msz vertę, jo iorės takų linijinis greitis turėtų būti apie 300 kartų didesnis u˛ viesos greitį vakuume. Todėl padaryta prielaida, kad kiekvienam elektronui visuomet būdingas ne tik tam tikras krūvis, rimties masė, bet ir sukinys, t. y. jam būdingos ypatingos savybės, be kurių jis neegzistuoja.

I grupės nesu˛adinto atomo visų elektronų, iskyrus valentinį, sukiniai tarpusavyje kompensuojasi. Tuomet atomo magnetinį momentą nusako valentinio elektrono sukinys. Jis, kaip ir bet koks kitas judesio kiekio momentas, kvantinėje mechanikoje ireikiamas (2.11.3) pavidalo lygybe:

(2.14.3)

čia s - sukinio kvantinis skaičius.

Sukiniui tinka bendra (2.11.6a) judesio kiekio momento erdvinio kvantavimo sąlyga, todėl jo projekcija vektoriaus B kryptimi parinktoje ayje Oz ireikiama itaip:

čia m_s — sukinio magnetinis kvantinis skaičius. Pagal (2.11.6a) lygybę jis gali įgyti tokias vertes:

t. y. i viso (2,c+l) skirtingą vertę. Tačiau terno ir Gerlacho bandymas parodė, kad

2s+1 = 2 arba s=1/2. (2.14.6)

Tuomet pagal (2.14.5) ir (2.14.6) elektrono sukinio magnetinis kvantinis skaičius¹

Pagal (2.14.3) ir (2.14.6) elektrono sukinys

(2.14.8)

Magnetiniame lauke is sukinys orientuojasi tik taip, kad jo projekcija ayje Oz

(2.14.9)

Kaip tik dėl to sidabro ar ličio atomų pluotelis nevienalyčiame magnetiniame lauke suskyla į du pluotelius.

Dėl sąveikos su indukcijos B magnetiniu lauku elektrono sukinys įgyja papildomą energijos kiekį

(2.14.10)

Tuomet 2.19 paveiksle parodytas kiekvienas energijos lygmuo suskyla dar į du labai artimus lygmenis. Sukinio sąlygojama spektro linijų skaidą magnetiniame lauke vadinama anomaliuoju Zėmano reikiniu.

Taigi elektrono būsena atome apraoma 4 kvantiniais skaičiais: pagrindiniu n, orbitiniu I, magnetiniu m ir sukinio magnetiniu m_s. Tokią pat ivadą matematikai 1928 m. gavo anglų fizikas P. Dirakas. Jis rėdingerio lygtį pritaikė reliatyvistiniam atvejui, t. y. elektrono judėjimą nagrinėjo 4 - matėje erdvėje. Tokia lygtis vadinama Dirako lygtimi. ios lygties sprendinyje yra jau 4 kvantiniai skaičiai — n, I, m ir m_s.

Kvantiniai uoliai?

uolis, kuris vyksta savaime i kvantinės 1 sistemos (atomo, molekulės, kristalo) vieno energetinio lygmens į kitą, I vadinamas savaiminiu, arba spontaniniu. Jie galimi tik i didesnės energijos (W_i) lygmens į ma˛esnės energijos (Wj) lygmenį. į uolį lydi energijos

e = W_i– Wj = hv

kvanto ispinduliavimas. Savaiminiam spinduliavimui būdinga tai, kad jis vyksta atsitiktinai. Negalima numatyti uolio prad˛ios laiko momento, — galima tik įvertinti tikimybę, kad per tam tikrą laiko tarpą jis įvyks. Dėl savaiminio uolio atsitiktinio pobūd˛io įvairūs atomai spinduliuoja nepriklausomai vienas nuo kito ne tuo pačiu laiko momentu. Dėl to jų elektromagnetinio spinduliavimo bangų fazės, poliarizacija (elektrinio lauko stiprumo vektorių E kryptys), spinduliavimo sklidimo kryptys yra įvairiausios, t. y. tarpusavyje nesuderintos. Todėl savaiminis spinduliavimas yra nekoherentinis, nors spinduliavimo da˛nis gali ir sutapti.

Savaiminius spindulinius uolius panagrinėkime tikimybės po˛iūriu. Sakykime, su˛adintoje būsenoje i, kurios energija W_i, atomų skaičius yra N_i. Jiems savaime pereinant į ma˛esnės energijos lygmenis, dydis N_i ma˛ėja. Tuomet ivestinė (dN_i/dt)_srodo ių elektronų savaiminio ma˛ėjimo spartą. Akivaizdu, kad ji turėtų būti tiesiog proporcinga N_t, arba

ioje lygybėje teigiamas proporcingumo koeficientas A_u vadinamas Einteino koeficientu. Jis apibūdina spontaninio spindulinio uolio i būsenos W_i į būseną W_j tikimybę. Minuso ˛enklas įraytas todėl, kad laikui bėgant dėl spindulinių uolių dydis N_i ma˛ėja, taigi ivestinė (dN_i/dt)_s<0. (2. 21.2) lygybėje atskyrę kintamuosius ir suintegravę gauname tokį energijos W_i atomų spontaninio ma˛ėjimo dėsnį:

čia N_i(0) - energijos W_i atomų skaičius pradiniu momentu (t=0). I pastarosios lygybės iplaukia, kad po tam tikro laiko

atomų skaičius energijos W_i lygmenyje spontanikai suma˛ėja e kartų. Dydis τ vadinamas būdingąja atomo gyvavimo trukme energijos W_i lygmenyje. Jeigu i io lygmens spontaniniai uoliai yra leistini, tai τ~10^-8s, jeigu draustini, — 10^-s-10^-3s arba dar ilgesni. Su˛adintųjų energijų W_i lygmenys, i kurių spontaninių uolių tikimybė yra palyginti ma˛a, vadinami metastabiliaisiais.

2. 1918 m. A. Einteinas atkreipė dėmesį, kad turi būti dar vienas spindulinių uolių tipas. Pagal jį, jeigu su˛adintame lygmenyje W_i esantį atomą veikia kintamasis elektromagnetinis laukas, kurio da˛nis v tenkina (2. 21.1) sąlygą, tai spindulinio uolio W_i→W_i tikimybė padidėja dyd˛iu P_ij. Toks spindulinis uolis vadinamas priverstiniu, arba indukuotuoju. Jo tikimybė tiesiog proporcinga į spinduliavimą sukeliančio elektromagnetinio lauko energijos tūriniam tankiui u(ν), t. y.

P_ij=B_iju (ν);

čia teigiamas proporcingumo koeficientas B_ij taip pat vadinamas Einteino koeficientu. Dėl io reikinio energijos W_i lygmenyje esančių atomų skaičiaus N, ma˛ėjimo sparta apraoma panaia į (2.21.2) lygybe:

(2.21.4)

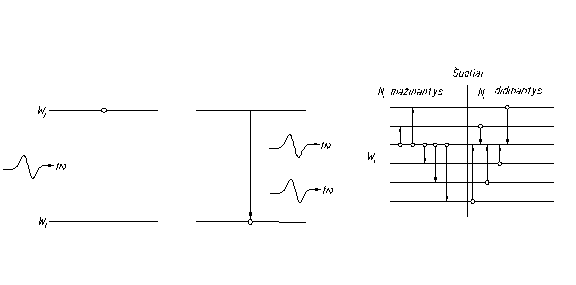
2.34 pav. 2.35 pav.

iuo atveju elektromagnetinio lauko veikiamas su˛adintas atomas (2.34 pav., d) pereina į ma˛esnės energijos būseną (2.34 pav., b). io priverstinio uolio metu ispinduliuoto fotono energija taip pat nusakoma (2.21.1)¹ lygybe. Indukuotojo spinduliavimo esminė ypatybė yra ta, kad naujai susidariusio fotono energija, da˛nis, sklidimo kryptis, poliarizacija, pradinė fazė yra tapatūs jį su˛adinusio fotono atitinkamoms charakteristikoms. Spinduliavimui taikant bangines sąvokas, būtų galima sakyti, kad indukuotasis spinduliavimas yra koherentus jį indukavusiam. Dėl to pirminis signalas sustiprinamas — tai ir yra kvantinio stiprintuvo veikimo esmė.

3. Būsenoje W_jesanti kvantinė sistema, sugėrusi energijos kiekį hν, kuris tenkina sąlygą

pereina į didesnės energijos W_i būseną — vyksta priverstinis arba indukuotasis absorbcinis uolis. Dėl energijos tvermės dėsnio spontaniniai uoliai Wj→W_i negalimi. Taigi absorbciniai uoliai būna tik priverstiniai. io reikinio tikimybė P_ij taip pat proporcinga krintančiosios elektromagnetinės energijos tūriniam tankiui u(ν), t. y.

čia B_ij — irgi vadinamasis Einteino koeficientas. Dėl ių uolių būsenoje W_i esančių atomų skaičius N_i didėja, jo kitimo sparta (dN_i/dt)_a yra teigiama ir pagal (2.21.4) analogiją u˛raoma itaip:

(2.21.5)

Nukleonai izotopai?

Protonas yra vandenilio, kurio masės skaičius A = 1, arba pročio, branduolys. Tai stabili subatominė dalelė. Ji turi elementarų teigiamą elektros krūvį e=l,6- 10^-19C. Protono rimties masė

m_p= 1,672648 • 1O^-27 kg ≈ 1,00759 a. m. v. ≈ 938,28 MeV. (4.1.1)

Protono masę ireikus elektrono rimties mase m_e, gaunama: m_p≈ 1836 m_e.

Protono sukinio kvantinis skaičius s=1/2, todėl jam taikomas Paulio principas. Protono magnetinis momentas

čia dydis

yra magnetinio momento vienetas, kuris vadinamas branduoliniu magnetonu. Taigi protono savasis magnetinis momentas apie 660 kartų ma˛esnis u˛ elektrono orbitini magnetinį momentą (Boro magnetoną). Bandymais nustatyta, kad protonas turi infrastruktūrą (˛r. 4.10 sk.), todėl jis nėra elementarioji dalelė.

Neutronas yra elektrikai neutrali subatominė dalelė, kurios rimties masė

m_n ≈ 1,674954-10^-27 kg ≈ 1,008665 a. m. v. ≈ 939,57 MeV. (4.1.2)

Ją sugretinę su elektrono rimties mase matome, kad m_n ≈ 1838,5 m_e. Taigi

M_n — m_p≈ 1,3 MeV ≈ 2,5 m_e

Neutrono, kaip ir protono, sukinio kvantinis skaičius s=1/2. Nors neutronas elektrikai neutralus, jo savasis magnetinis momentas

Dėl to, kad laisvojo neutrono rimties masė yra didesnė u˛ protono masę, neutronas yra nestabilus. Veikiant vadinamajai silpnajai sąveikai (˛r. 4.3 sk.), laisvasis neutronas spontanikai virsta protonu ir elektroniniu antineutrinu. Neutronas, kaip ir protonas, turi infrastruktūrą, todėl jis nėra elementarioji dalelė.

Elementariųjų dalelių klasifikacija?

Kol nebuvo atrasti kvarkai, hadronai buvo laikomi elementariosiomis dalelėmis. Da˛nai jie taip vadinami ir dabar. Tačiau pagal kvarkų teoriją mezonai sudaryti i kvarko ir antikvarko, o barionai — i atitinkamų trijų kvarkų ar antikvarkų (˛r. 9 lent.). Taigi turinčius infrastruktūrą had-ronus netinka vadinti elementariosiomis dalelėmis. Mūsų dienų fizikos po˛iūriu elementariųjų dalelių klasifikacija pateikta 10 lentelėje. Joje nesuraytos elementariosios antidalelės (antikvarkai ir antileptonai).

Dvi elementariųjų dalelių eimos — kvarkai ir leptonai — yra med˛iaginės dalelės. Visos ios dalelės yra fermionai (s=1/2).

Kitą elementariųjų dalelių grupę sudaro med˛iagos dalelių kuriamų laukų kvantai. Jie kaip tik yra dalelių sąveikos neikliai. I jų labiausiai ˛inomas elektromagnetinio lauko kvantas fotonas. Pagal kvantinę mechaniką virtualieji fotonai yra elektromagnetinės sąveikos neikliai, vektoriniai bozonai — silpnosios, o gliuonai — kvarkų stipriosios sąveikos neikliai. Visų ių elementariųjų dalelių sukinio kvantinis skaičius s=1, todėl jos yra bozonai.

I kvantinės mechanikos principų iplaukia, kad turėtų egzistuoti gravitacinio lauko kvantas gravitonas. Jis turėtų būti gravitacinės sąveikos neiklis. Spėjama, kad jo sukinio kvantinis skaičius s = 2. Taigi jis taip pat turėtų būti bozonas. Tačiau jo sąveika su med˛iaga labai silpna, todėl eksperimentikai aptikti gravitoną yra labai sunku. iuolaikiniai teoriniai modeliai numato ir kitas elementariąsias daleles, pavyzd˛iui, gravitiną ir kt., tačiau bandymais jos neaptiktos. Taigi iuo metu ˛inomos dvi stambesnės elementariųjų dalelių grupės: med˛iagos dalelės ir jų sąveikos neikliai.

Politica de confidentialitate | Termeni si conditii de utilizare

DISTRIBUIE DOCUMENTUL

Vizualizari: 2047
Importanta:

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Distribuie URL
https://www.scrigroup.com/limba/lituaniana/255/Dielektrikai-elektriniame-lauk55687.php

Adauga cod HTML in site
<a href="https://www.scrigroup.com/limba/lituaniana/255/Dielektrikai-elektriniame-lauk55687.php" target="_blank" title=" - https://www.scrigroup.com/limba/lituaniana/255/Dielektrikai-elektriniame-lauk55687.php">Dielektrikai elektriniame lauke (orientacine poliarizacija, joninė poliarizacija)</a>

Dielektrikai elektriniame lauke (orientacine poliarizacija, joninė poliarizacija)

elektra

DOCUMENTE SIMILARE

DISTRIBUIE DOCUMENTUL

Comenteaza documentul: