ELEKTRONINËS OPTIKOS OBJEKTAI IR MATEMATINIS APARATAS

ELEKTRONINËS OPTIKOS OBJEKTAI IR MATEMATINIS APARATAS

Šios dalies pirmajame poskyryje susipažinsime su pagrindinëmis EO s¹vokomis, terminija, klasifikacija ir svarbiausiais uždaviniais, sprendžiamais apibendrintose EO sistemose, t.y. sistemose, kuriose áelektrinta dalelë (daugeliu atvejø ši dalelë yra elektronas), juda mišriame – elektriniame ir magnetiniame – lauke. Èia pateikiami ir pagrindiniai šiø uždaviniø sprendimo metodai.

Antrajame ir treèiajame poskyriuse prisiminsime matematinio aparato, naudojamo tolesnëse vadovëlio dalyse, pagrindinius momentus. Be to, kadangi elektriniø ir magnetiniø laukø analizë grindžiama Maksvelo dësniais, sutrumpinta forma èia pateikiamos šiø dësniø išraiškos.

Elektroninës optikos pagrindinës s¹vokos

EO – fizikos ir elektronikos dalis, nagrinëjanti áelektrintø daleliø judesá elektriniuose ir magnetiniuose laukuose, áelektrintø daleliø srautø formavim¹, fokusuotê, kreipim¹, vaizdø sudarym¹ ekrane (taikinyje), srautø fokusuotës bei kreipimo iškraipymus (aberacijas).

Áelektrintø daleliø judëjimas elektriniame ar magnetiniame lauke kai kuriais požiûriais analogiškas šviesos sklidimui atitinkama aplinka, todël kai kuriuos optikos dësningumus ir s¹vokas galima perkelti á EO sritá:

-EO vartojamas elektroninis-optinis lûžio rodiklis, formuojami elektroniniai lêšiai, prizmës, veidrodžiai. Elektroniniai lêšiai apibûdinami optiniu stiprinimu, pagrindiniais židiniais, pagrindinëmis plokštumomis ir pan.

-EO skirstoma á geometrinê EO ir banginê EO.

Geometrinë EO nagrinëja áelektrintø daleliø judëjim¹ elektriniuose ir magnetiniuose laukuose, jø fokusuotê, kreipim¹ ir pan., neávertindama banginiø daleliø savybiø. Banginëje EO á judanèi¹ dalelê žiûrima kaip á de Broilio bang¹, ir nagrinëjami specifiniai tokios bangos sklidimo ypatumai – difrakcija ir interferencija. De Broilio bangos ilgis l=h/(m^.v), (h =6,626176(36)^.10^-34 J^.s – Planko konstanta (skaièius skliausteliuose parodo paskutiniøjø dviejø reikšminiø skaitmenø skaièiaus standartiná nuokrypá), v ir m – áelektrintos dalelës greitis ir masë). Bangos ilgis net palyginti lëtiems elektronams yra labai mažas, pvz., elektrono, ágreitinto 100 V potencialø skirtumu, de Broilio bangos ilgis l=1,25^.10^-10 m ir, nagrinëdami daugum¹ EO klausimø, banginiø elektrono savybiø galime nepaisyti. Tik išskirtiniais atvejais, pvz., nagrinëjant ribinê elektroninio mikroskopo skiriam¹j¹ geb¹, neišvengiamai tenka taikyti banginës EO metodus, todël toliau ávairius klausimus nagrinësime vien geometrinës EO metodais.

Pagal Heizenbergo neapibrëžtumo s¹lyg¹, elektrono greitis v ir padëtis x (koordinatë) negali bûti tiksliai apibrëžti, t.y. ; èia m₀=9,109534(47)^.10^-31 kg elektrono rimties masë. Árašê h ir m₀ reikšmes, gauname Jeigu greièio paklaida =0,1% ir v³10⁶ m/s (toks elektrono greitis yra elektroniniuose vamzdeliuose), tai Dx³0,73^.10^-6 m. Todël galima tarti, kad elektrono padëtis ir jo greitis apibrëžiami tiksliai.

Elektrono greitis bet kuriame erdvës taške priklauso nuo to taško elektrinio lauko potencialo j Elektrono energijos tvermës dësná reliatyvistinëje fizikoje apibrëžia Einšteino lygtis: ; èia - -reliatyvus elektrono masës pokytis, - šviesos greitis vakuume, -elektrono krûvis. Išreiškê elektrono greitá v, gauname:

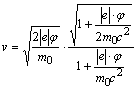=.  (1.1)

Elektrono greitis v, esant ávairiems lauko potencialams pateiktas 1 lentelëje. Toje paèioje lentelëje pateiktas ir santykinis elektrono greitis elektrono greièio, apskaièiuoto pagal klasikinê fizik¹, kai m=m₀=const., atžvilgiu.

Iš lentelës rezultatø galima daryti išvad¹, kad reliatyvius procesus reikia ávertinti, kai j > 50 kV. Kai j < 50 kV, elektrono greitá galima skaièiuoti klasikiniu bûdu:

(1.2)

Dažniausiai vartojamos geometrinës EO s¹vokos:

-elektronø srautas – tai apytiksliai á vien¹ pusê judantys elektronai;

-elektronø pluoštas – tai elektronø srautas, kurio išorinës ribos apibrëžtos. Be to, vienos ašies kryptimi šis srautas daug ilgesnis nei kitø ašiø kryptimis;

-elektronø spindulys – tai labai plonas elektronø pluoštas, kurio pëdsak¹ vamzdelio ekrane galime laikyti tašku.

Judanèius elektronus veikia ne tik išoriniai elektriniai ir magnetiniai laukai, kuriami riteliø sroviø, ákrautø elektrodø, feromagnetikø, nuolatiniø magnetø ir pan., bet ir paèiø judanèiø elektronø kuriami elektriniai ir magnetiniai laukai. Tai ypaè ryšku, kai elektronai juda spinduliu (labai sufokusuoti), turi didelá erdvinio krûvio tanká ar juda dideliu greièiu.

Magnetiniai elektronø kuriami laukai vertintini tik tada, kai elektronø greitis artimas šviesos greièiui, todël daugeliu atvejø jø poveikio galima nepaisyti. Tuo tarpu elektriniai elektronø kuriami laukai yra efektyvesni tada, kai elektronø greitis nedidelis (ilga poveikio trukmë) ir elektronø spindulyje yra didelis erdvinio krûvio tankis (didelis elektronø tankis). Taigi EO dar dalijama á dvi dalis: EO, nevertinanti erdvinio krûvio átakos, ir intensyviø elektronø pluoštø EO.

Skirstymo kriterijumi laikoma erdvinio krûvio koeficiento (perveanso) reikšmë ; èia I – elektronø pluošto (spindulio) srovë; j – elektronø greitinimo potencialas. Jei P < 10^-2 mA/V^3/2, tai erdvinio krûvio átakos galima nepaisyti. Ši s¹lyga galioja kineskopams (s¹lygiškai), oscilografiniams vamzdeliams; tuo tarpu klistronuose, magnetronuose, bëganèiosios bangos lempose, elektroniniuose mikroskopuose, projekciniuose kineskopuose, galinguose technologiniuose EO árenginiuose bûtina vertinti erdvinio krûvio átak¹.

Pagrindinë klasikinës EO lygtis, aprašanti elektrono judesá elektromagnetiniame lauke, yra

; (1.3)

èia m=m₀, q=-e, - elektrinio lauko stiprumas, - magnetinio lauko indukcija.

Taigi, norëdami rasti elektrono judesio dësná [x(t), y(t), z(t)], turime žinoti elektrinio lauko stiprumo , magnetinës indukcijos vektorius ir elektrinio lauko potencial¹ j tuose erdvës taškuose, per kuriuos skrieja elektronas. Šá uždaviná galima sprêsti dviem metodais:

1. Naudojant šiuolaikinê teorinê elektriniø ir magnetiniø laukø skaièiavimo bazê bei jau pakankamai galing¹ skaièiavimo technik¹, remiantis duotos EO sistemos konstrukcijos parametrais, skaièiuojami elektriniai ir magnetiniai laukai reikalinguose erdvës taškuose. Tai galima atlikti dviem bûdais:

a) elektriniai ir magnetiniai laukai skaièiuojami fiksuotuose (baziniuose) ribotos erdvës taškuose. Kadangi bendruoju atveju šie taškai nesutaps su elektronø trajektorijai skaièiuoti reikalingais taškais, laipsniniais (taip pat ir ortogonaliaisiais) polinomais ar kitomis funkcijomis atliekamas trimatis analitinis laukø aprašymas (trimatë aproksimacija arba interpoliacija). Kadangi baziniuose taškuose laukai apskaièiuojami gana tiksliai ir trimatë aproksimacija yra sudëtingesnis uždavinys, tai, jei baziniø taškø yra pakankamai daug, optimalus analitinis laukø aprašymas yra trimatë tiesinë (kraštiniu atveju – kvadratinë) interpoliacija. Tai galima pagrásti tuo, kad elektriniai ir magnetiniai laukai bekrûvëje ir besrovëje erdvëje yra potencialiniai, t.y. jiems galioja Laplaso lygtis

(1.4)

Laplaso lygties sprendinys yra harmoninë funkcija, kurios viena iš savybiø yra ta, kad potencialas j sferos centre lygus vidutinei sferos paviršiaus potencialo reikšmei:

Jei lauko potencialas j yra tiesinë koordinaèiø funkcija, tai, naudodami tiesinê interpoliacij¹, paklaidos negausime. Jei baziniø taškø nepakanka, tenka taikyti sudëtingesnê kvadratinê interpoliacij¹.

Šis bûdas patogus tuo, kad galima atskirti laukø skaièiavimo ir elektronø trajektorijø skaièiavimo procedûras: skaièiuodami trajektorijas, turime turëti tik laukø stiprumø baziniuose taškuose masyvus arba aproksimaciniø polinomø koeficientus. Taèiau šis bûdas tinka tik tiesinei sistemai, t.y. kai laukø potencialai yra tiesiogiai proporcingi elektrodø potencialams ar riteliø srovëms. Jei EO sistema turi feromagnetiniø elementø, ji bendruoju atveju tampa netiesine sistema.

b) laukai skaièiuojami tuose taškuose, kuriø reikalauja elektronø trajektorijø skaièiavimo programa. Šiuo atveju taškø yra nedaug, ir šá bûd¹ galima taikyti tiek tiesinëms, tiek netiesinëms sistemoms, bet laukø skaièiavimo ir trajektorijø skaièiavimo programos yra susipynusios.

2. Laukus galima ne skaièiuoti, o matuoti. Šis metodas taikytinas tada, kai skaièiuoti laukus labai sudëtinga: turime sudëtingos konstrukcijos laukø šaltinius, yra daug skirtingos prigimties laukø šaltiniø ir pan. Be to, modeliuojant (skaièiuojant) laukus, sunku sudaryti matematiná modelá, adekvatø fiziniam modeliui, todël, matuodami laukus, ávertiname visus veiksnius, turinèius átakos laukø konfigûracijai ir stiprumui. Magnetinius laukus matuoti nesudëtinga, tuo tarpu elektriniø laukø matavimas yra komplikuotas dalykas ir jis dažnai keièiamas fiziniu modeliavimu.

Galimas ir treèias uždavinio sprendimo metodas: elektriniai laukai skaièiuojami, o magnetiniai – matuojami.

1.2. Pagrindinis matematinis aparatas

Pagrindinis matematinis aparatas, naudojamas elektromagnetiniams laukams skaièiuoti, yra vektorinë analizë, kurios pagrindinës s¹vokos yra skaliaras, vektorius ir tenzorius. Bendruoju atveju laukø skaliarai ir vektoriai yra koordinaèiø ir laiko funkcijos. Pagrindiniai operatoriai, atliekantys kokius nors veiksmus su elektromagnetiniø laukø skaliarais ar vektoriais, yra kreivinis, paviršinis ir tûrinis integralas, taip pat specialûs diferencialiniai operatoriai. Paaiškinsime šiø pagrindiniø operatoriø esmê.

Kreivinis vektoriaus integralas (1.1 pav.) – skaliarinis dydis, proporcingas vektoriaus atliktam darbui kelyje . Jei šis kelias sudaro uždar¹ kontûr¹, toks integralas vadinimas cirkuliacija ir užrašomas ; èia -vektoriø ir d skaliarinë sandauga:

(1.5)

Paviršinis vektoriaus integralas skaliarinis dydis, proporcingas vektoriaus srautui per paviršiø S (1.2 pav.). Jei paviršius uždaras, gauname sraut¹ per uždar¹ paviršiø ; èia d- vektorinis plokštumos elementas, kurio modulis lygus elemento plotui, o kryptis sutampa su paviršiaus išorinës normalës kryptimi.

Tûrinis vektoriaus integralas - tai vektorius, kurio dydis proporcingas tûriui V ir lygus atstojamojo vektoriaus moduliui, o kryptis sutampa su atstojamojo vektoriaus kryptimi.

Diferencialinis nabla operatorius Ñ (Hamiltono operatorius).

(1.6)

Tai simbolinis vektorius, turintis ir vektoriniø ir diferencijavimo savybiø. Operuojama skaliarinëmis ir vektorinëmis funkcijomis.

Laplasianas (Laplaso operatorius)

(1.7)

Tai skaliarinis diferencialinis operatorius. Atliekamos operacijos su skaliarinëmis ir vektorinëmis funkcijomis.

Skaliarinës funkcijos gradientas

gradj = .  (1.8)

Tai vektorius, parodantis didžiausio skaliarinës funkcijos j kuriame nors taške didëjimo kryptá ir dydá; èia - normalë á ekvipontecialiná paviršiø potencialo didëjimo kryptimi (1.3 pav.). Dekartinëje koordinaèiø sistemoje

(1.9)

Vektorinës funkcijos divergencija

(1.10)

Tai vektorinio lauko skaliarinë funkcija tûryje DV, lygi šio lauko vektoriaus srauto per uždar¹ paviršiø S, kuris gaubia tûrá DV, santykiui su tûriu DV, kai šis tûris traukiasi á tašk¹. Jei tûryje DV yra vektoriaus šaltinis, tai ; jei šaltiniø nëra, - .

Vektorinës funkcijos rotacija

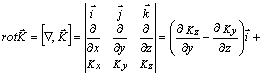
(1.11)

èia - vektorinë ir vektoriø sandauga. Jei vektoriaus cirkuliacija uždaru kontûru L, ribojanèiu paviršiø DS, yra , tai , t.y. vektoriaus rotacijos dedamoji paviršiaus DS normalës kryptimi yra vektoriaus cirkuliacijos kontûru L santykis su ploteliu DS, kai (1.4 pav.), todël yra toks vektorius , kai, sukinëjant plotelá DS, gaunama maksimali jo reikšmë. Teigiama kryptis priklauso nuo integravimo krypties ir nusakoma dešiniojo sraigto taisykle (1.4 pav.). Rotacija susijusi su sûkuriniais laukais, ir, kai kuriame nors taške nëra sûkuriná vektoriná lauk¹ kurianèio šaltinio, šio lauko rotacija lygi nuliui. Tokiu atveju vektorinis laukas gali bûti aprašomas skaliarinës funkcijos j gradientu, ir jis vadinamas potencialiniu lauku.

Pagrindinës vektoriniø operacijø taisyklës

(1.12)

(1.13)

(1.14)

Pagrindinës antrosios eilës vektoriniø operacijø taisyklës:

- sûkurinis laukas neturi ištakos ir santakos,  (1.15)

- potencialinis laukas neturi sûkurio, (1.16)

(1.18)

èia .

Integralinës teoremos. Tai teoremos, kurias naudojame, pereidami nuo vienos integralinës lauko aprašymo formos prie jai ekvivalenèios. Pagrindinës integralinës teoremos yra:

-divergencijos teorema

(1.19)

èia V - tûris, apribotas uždaro paviršiaus S, kurio teigiama normalë yra nukreipta á išorê;

-rotacijos teorema

(1.20)

-gradiento teorema

(1.21)

-Gauso teorema

(1.22)

-Stokso teorema

(1.23)

t.y. vektoriauscirkuliacija uždaru konturu L yra lygi šio vektoriaus rotacijos srautui per paviršiø S, užtempt¹ ant kontûro L. Plotelio ir kontûro elemento kryptys tenkina dešiniojo sraigto taisyklê.

Diferencialinës ir integralinës Maksvelo lygèiø formos

Maksvelo lygtys yra pagrindinës elektromagnetinio lauko lygtys, kurios gali bûti aprašomos diferencialine ar integraline forma. Dalinis diferencialinio aprašymo atvejis yra kompleksinë aprašymo forma, kai laukas kinta harmonine laiko funkcija.

Integralinës Maksvelo lygtys parodo laukø parametrø ryšá daugelyje erdvës taškø, tuo tarpu diferencialinë Maksvelo lygèiø forma parodo šiø parametrø ryšá tame paèiame erdvës taške tam tikru laiko momentu.

Pilnutinës srovës dësnis (I Maksvelo lygtis):

- diferencialinë forma,

- kompleksinë forma,

- integralinë forma;

èia -magnetinio lauko stiprumas, - laidumo srovës tankis, -vektoriai, kintantys harmonine laiko funkcija, pvz.. Slinkties srovë ,kaip ir laidumo srovë , sukuria magnetiná lauk¹; kintamas elektrinis laukas sukuria magnetiná lauk¹; slinkties ir laidumo srovë sudaro pilnutinê srovê.

Elektromagnetinës indukcijos dësnis(II Maksvelo lygtis):

- diferencialinë forma,

- kompleksinë forma, (1.25)

- integralinë forma;

èia - elektrinio lauko stiprumas, - magnetinio lauko indukcija. Kintamas magnetinis laukas (magnetinë indukcija) sukuria elektriná lauk¹, kurio kryptis susijusi su kryptimi ir nustatoma pagal dešiniojo sraigto taisyklê.

Magnetiniø jëgos linijø netrûkumas (III Maksvelo lygtis).

- diferencialinë forma,

- kompleksinë forma, (1.26)

- integralinë forma.

Magnetinis srautas per uždar¹ paviršiø lygus nuliui tik tada, kai magnetiniø jëgø linijos yra uždaros (neturi nei pradžios, nei pabaigos).

Apibendrinta Gauso teorema (IV Maksvelo lygtis)

- diferencialinë forma,

- kompleksinë forma, (1.27)

- integralinë forma;

èia q – laisvasis elektrinis krûvis erdvëje, apribotas paviršiaus S; r - šio laisvojo krûvio tankis. Elektrinës slinkties srautas per uždar¹ paviršiø lygus laisviesiems krûviams, esantiems šio paviršiaus viduje.

Šios pagrindinës keturios Maksvelo lygtys dar papildomos ryšio lygtimis kokioje nors konkreèioje izotropinëje aplinkoje:

(1.28)

èia - dielektriko (aplinkos) poliarizacijos vektorius (poliarizuotumas); - aplinkos absoliutinë dielektrinë skvarba; - aplinkos absoliutinë magnetinë skvarba; - vakuumo absoliutinë dielektrinë ir magnetinë skvarbos; e m - aplinkos santykinë dielektrinë ir magnetinë skvarbos; g - aplinkos elektrinis laidumas; - išorinio elektrinio lauko stiprumas; - aplinkos ámagnetinimo vektorius (tûrio vieneto magnetinis momentas).

Savikontrolës klausimai

Kuo panašios ir kuo skiriasi šviesos optika ir elektroninë optika?

Kokiomis s¹lygomis reikia ávertinti reliatyvistinê elektrono masê ir elektronø spindulio kuriamus laukus?

Kokie yra du pagrindiniai EO uždaviniø skaièiavimo metodai?

Paaiškinkite lauko gradiento, divergencijos ir rotacijos fizikinê prasmê.

Kuo skiriasi vektoriaus cirkuliacija nuo rotacijos?

Paaiškinkite Maksvelo lygèiø diferencialinê, integralinê ir kompleksinê formas.

Užrašykite statiniø laukø Maksvelo lygtis.