CATEGORII DOCUMENTE
Afaceri Calculatoare Casa masina Didactica pedagogie Diverse Educatie Finante Geografie Istorie & politica Legislatie Limba Management Sanatate Tehnologie

Bulgara	Ceha slovaca	Croata	Engleza	Estona	Finlandeza	Franceza
Germana	Italiana	Letona	Lituaniana	Maghiara	Olandeza	Poloneza
Sarba	Slovena	Spaniola	Suedeza	Turca	Ucraineana

įstatymai	įvairių	Apskaitos	Architektūra	Biografija	Biologija	Botanika	Chemija
Ekologija	Ekonomika	Elektra	Finansai	Fizinis	Geografija	Istorija	Karjeros
Kompiuteriai	Kultūra	Literatūra	Matematika	Medicina	Politika	Prekyba	Psichologija
Receptus	Sociologija	Technika	Teisė	Turizmas	Valdymas	vietimas

KIETŲJŲ KŪNŲ ELEKTRINIS LAIDUMAS

elektra

+ Font mai mare | - Font mai mic


DOCUMENTE SIMILARE

KIETŲJŲ KŪNŲ ELEKTRINIS LAIDUMAS

iame skyriuje aptarsime, nuo ko, kaip ir kodėl priklauso puslaidininkių, metalų ir lydinių elektrinis laidumas bei juose tekančios srovės.

1. Krūvininkų dreifas ir relaksacija

Nagrinėkime kietojo kūno bandinį, kuriame yra laisvųjų elektronų. Kai iorinis elektrinis laukas neveikia, laisvieji elektronai juda chaotikai (1 pav., a) dėl susidūrimų su kietojo kūno gardele. Sukūrus kietajame kūne elektrinį lauką, kurio stipris , be chaotikojo elektronų judėjimo, vyksta jų kryptingas slinkimas prieinga elektriniam laukui kryptimi (1 pav., b). Toks slinkimas vadinamas dreifu. Vidutinis io kryptingo slinkimo greitis vadinamas dreifo greičiu.

Aptarkime, kaip dreifo greitis priklauso nuo elektrinio lauko stiprio.

Elektrinis laukas veikia elektroną jėga, kurios modulis

; (1)

čia – elektrono krūvio absoliutinė vertė.

Veikiant jėgai , elektrono greitis turėtų nuolat didėti. Tačiau kietajame kūne elektronui judėti trukdo gardelė. Susidurdamas su gardele elektronas praranda kryptingo judėjimo greitį. Gardelės įtaką elektrono judėjimui galima įvertinti pasiprieinimo jėga , kuri proporcinga dreifo greičiui, bet yra prieingos krypties:

(2)

čia – elektrono efektinė masė, – proporcingumo koeficientas.

Atsi˛velgiant į jėgas ir , elektrono kryptingą judėjimą galima aprayti lygtimi:

; (3)

čia – pagreitis.

Įraę į (3) jėgų iraikas (1) ir (2) ir atsi˛velgę, kad , gauname:

. (4)

I ios lygties matyti, kad, pradėjus veikti elektriniam laukui, laisvųjų kietojo kūno elektronų greitis didėja. Kartu didėja ir pasiprieinimo jėga . Jai didėjant, ma˛ėja elektronų pagreitis. Kai jėgos ir susilygina, pagreitis suma˛ėja iki nulio. Tada elektronai slenka pastoviu greičiu, kuris pagal (4) ireikiamas formule:

. (5)

ioje lygtyje proporcingumo koeficientas

(6)

vadinamas elektronų judrumu. Kai 1, tai pagal (5) . Vadinasi, kai elektrinio lauko stipris lygus vienetui, krūvininkų judrumo skaitinė vertė lygi dreifo greičio skaitinei vertei.

Verta pastebėti, kad, jeigu nebūtų pasiprieinimo jėgos , tai, veikiant elektriniam laukui, elektronų pagreitis nekistų, jų kryptingo judėjimo greitis nuolat didėtų. Tada kietojo kūno elektrinis laidumas būtų be galo didelis.

Vadinasi, elektronų dreifo greitį kietajame kūne ir kietojo kūno elektrinį laidumą riboja elektronų susidūrimai su kristaline gardele.

Dabar mintyse sudarykime kietajame kūne stačiakampį gretasienį, kurio pagrindas statmenas elektrinio lauko krypčiai (2 pav.). Stačiakampio gretasienio pagrindo plotas lygus vienetui, auktinė yra . Tada stačiakampio gretasienio tūris . Jame yra elektronų. Visi ie elektronai per laiko vienetą pereina per stačiakampio gretasienio pagrindą. Tada srovės tankis kietajame kūne (krūvis pratekantis per laiko vienetą pro ploto vienetą) ireikiamas formule:

. (7)

Įraę į (7) dreifo greičio iraiką, turėsime:

. (8)

Pagal ią formulę srovės tankis kietajame kūne yra tiesiai proporcingas elektrinio lauko stipriui. Formulė ireikia Omo (Ohm) dėsnį. Joje – savitasis (specifinis) nagrinėjamo kietojo kūno laidumas.

Pagal (8), kai kietojo kūno krūvininkai yra tik elektronai, to kietojo kūno savitasis elektrinis laidumas ireikiamas formule:

. (9)

Puslaidininkių elektrinį laidumą lemia elektronai ir skylės. Todėl

; (10)

čia – skylių koncentracija, – jų judrumas.

Taigi kietojo kūno savitąjį elektrinį laidumą ir jo savitąją var˛ą lemia krūvininkų koncentracija ir jų judrumas.

Dabar tarkime, kad ilgą laiką veikęs elektrinis laukas laiko momentu 0 ijungiamas. Tada dėl susidūrimų su gardele elektronų kryptingo slinkimo greitis pradeda ma˛ėti – atsistato elektrinio lauko sutrikdyta elektronų sistemos pusiausvyra. Toks fizinės sistemos pusiausvyros atsistatymas po jos sutrikdymo vadinamas relaksacija.

Kai elektrinis laukas neveikia, (4) lygtis tampa paprastesnė:

ios lygties sprendinys ireikiamas formule

; (11)

čia – pradinis dreifo greitis, – konstanta – elektrono dreifo greičio arba impulso relaksacijos trukmė.

Pagal (11), ijungus elektrinį lauką, elektronų dreifo greitis ma˛ėja eksponentiniu dėsniu. Per laiką jis suma˛ėja e kartų. Relaksacijos trukmę galima susieti su krūvininko vidutiniu laisvuoju keliu. Jeigu elektronas kryptingo judėjimo greitį praranda po vieno susidūrimo su gardele, elektrono laisvasis kelias ireikiamas formule ; čia – vidutinis elektrono greitis. Da˛nai elektronas kryptingo judėjimo greitį praranda tik po susidūrimų su gardele. Tada . I čia

. (12)

Elektrono greitis susideda i dviejų dedamųjų – iluminio judėjimo greičio ir dreifo elektriniame lauke greičio . Da˛niausiai iluminio judėjimo greitis būna daug didesnis u˛ dreifo greitį. Tada galima laikyti, kad .

Pagal (6) ir (12) krūvininkų judrumas ireikiamas formule

. (13)

I ios formulės matyti, kad krūvininkų judrumas yra ribotas dėl baigtinio laisvojo kelio. Laisvąjį kelią riboja krūvininkų sklaida, atsirandanti dėl krūvininkų susidūrimų su kristaline gardele.

Nagrinėdami krūvininkų sklaidą kristale, turime prisiminti jų, kaip mikrodalelių, dvilypumą ir bangines savybes. Bangos neatsispindi nuo periodinių netolygumų, tarp kurių atstumas daug ma˛esnis u˛ bangos ilgį. Taigi elektronai ir skylės, kaip de Broilio bangos, neatsispindi nuo arti vienas kito esančių kietojo kūno gardelės mazgų. Krūvininkų sklaidą sukelia jų susidūrimai su gardelės defektais, atsirandančiais dėl priemaių, gardelės iluminių virpesių ir kitų anksčiau aptartų prie˛asčių.

2. Puslaidininkių krūvininkų judrumas

Grynajame puslaidininkyje nėra priemaių. Todėl krūvininkų laisvąjį kelią ir judrumą lemia kristalinės gardelės iluminiai defektai. Virpant gardelei, jos mazgai kai kuriose kristalo vietose suartėja, kitose vietose – nutolsta vienas nuo kito. Taip gardelėje atsiranda netolygumų, nuo kurių gali atsispindėti krūvininkus atitinkančios de Broilio bangos. Kylant temperatūrai, iluminių defektų ir juos atitinkančių kvazidalelių – fononų – koncentracijos auga. Todėl didėja krūvininkų sklaida, o krūvininkų vidutinis laisvasis kelias trumpėja: . Neisigimusios sistemos dalelių vidutinis iluminio judėjimo greitis, kaip ˛inome, didėja kylant temperatūrai: . Kad krūvininkas prarastų kryptingo judėjimo greitį pakanka vieno susidūrimo su fononu (1). Tada pagal (13) formulę

. (14)

Taigi, kylant temperatūrai, krūvininkų judrumas grynajame puslaidininkyje ma˛ėja.

Priemaiiniame puslaidininkyje krūvininkų sklaidą sukelia gardelės iluminiai defektai ir jonizuoti priemaių atomai. ˇemųjų temperatūrų srityje gardelės iluminių defektų ir fononų koncentracijos būna nedidelės. Tuomet krūvininkų judrumą lemia jonizuotų priemaių atomų sukelta sklaida.

Priemaių koncentracija nepriklauso nuo temperatūros. Todėl krūvininkų vidutinis laisvasis kelias, kylant temperatūrai, nesikeičia. Krūvininkų vidutinis iluminio judėjimo greitis, kylant temperatūrai, didėja: . Judėdamas didesniu greičiu, krūvininkas greičiau įveikia jono sukurto elektrinio lauko sritį. Jo trajektorija ma˛iau pasikeičia. Taigi, kylant temperatūrai, skaičius susidūrimų, po kurių krūvininkas praranda kryptingo judėjimo greitį, padidėja. Taip samprotaujant įrodoma, kad . Tada pagal (13) formulę

. (15)

Vadinasi, ˛emųjų temperatūrų srityje, kylant temperatūrai, krūvininkų judrumas priemaiiniame puslaidininkyje didėja.

Auktų temperatūrų srityje krūvininkų sklaidą priemaiiniame puslaidininkyje lemia jų sąveika su fononais. Todėl auktų temperatūrų srityje, kylant temperatūrai, krūvininkų judrumas ma˛ėja.

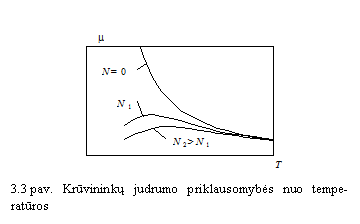
3 paveiksle atvaizduotos puslaidininkių krūvininkų judrumo priklausomybės nuo temperatūros kreivės. Jas panagrinėjus matyti, kad auktų temperatūrų srityje krūvininkų judrumas nepriklauso nuo priemaių koncentracijos . ˇemų temperatūrų srityje, didėjant priemaių koncentracijai, judrumas ma˛ėja. Did˛iausias priemaiinio puslaidininkio krūvininkų judrumas pasireikia vidutinių temperatūrų srityje. Didėjant priemaių koncentracijai, maksimalus judrumas ma˛ėja, maksimalaus judrumo takas slenka auktesnių temperatūrų kryptimi.

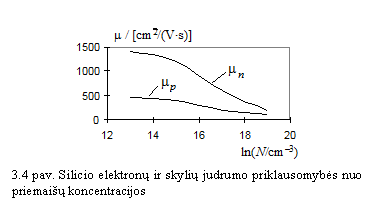
4 paveiksle pateiktos kreivės, vaizduojančios, kaip silicio krūvininkų judrumas 300 K temperatūroje priklauso nuo priemaių koncentracijos. Kai priemaių koncentracija nedidelė (iki 10¹⁵ cm^–3), krūvininkų judrumas nuo priemaių koncentracijos beveik nepriklauso, nes vyrauja fononinė krūvininkų sklaida. Kai priemaių koncentracija didesnė kaip 10¹⁵ cm^–3, pradeda reiktis jonizuotų priemaių atomų sukelta sklaida. Tada, didėjant priemaių koncentracijai, judrumas ma˛ėja. Kai 10¹⁷ cm^–3, priemaiiniame puslaidininkyje dominuoja priemaių sukelta krūvininkų sklaida. Tada , nes krūvininko vidutinis laisvasis kelias yra tiesiai proporcingas atstumui tarp priemaių atomų, kuris apytikriai lygus .

I 4 paveikslo dar matyti, kad silicio laidumo elektronų ir skylių judrumai nevienodi. Elektronų judrumas beveik tris kartus didesnis u˛ skylių judrumą.

Be aptartų prie˛asčių, krūvininkų judrumą gali riboti jų sklaida dėl susidūrimų su neutraliais priemaių atomais, taip pat pavirinė, dislokacinė sklaida ir pan. Kai veikia keli sklaidos mechanizmai, efektinis judrumas ireikiamas formule:

; (16)

čia – judrumo reikmė, gaunama atsi˛velgiant tik į -ąjį sklaidos mechanizmą.

1 u˛duotis

Elektronų judrumas grynajame silicyje 300 K temperatūroje yra 1500 cm/(V s). Laikydami, kad elektrono efektinė masė lygi jo ramybės masei, apskaičiuosime vidutinį laisvąjį elektrono kelią ir palyginsime jį su gardelės konstanta a=0,543 nm.

Sprendimas

Pagal (13)

Taikant klasikinę Maksvelo-Bolcmano statistiką įrodoma, kad elektrono vidutinis iluminio judėjimo greitis yra artimas vidutiniam kvadratiniam greičiui ir ireikiamas formule:

Taikydami ią formulę gautume, kad

Tuomet

Puslaidininkių elektrinis laidumas

Puslaidininkio elektrinį laidumą lemia laidumo elektronai ir skylės. Elektrinis laidumas ireikiamas (10) formule:

Grynajame puslaidininkyje laidumo elektronų ir skylių koncentracijos vienodos . Tada

. (17)

Grynojo puslaidininkio savųjų krūvininkų koncentracija ir judrumas priklauso nuo temperatūros. Pagal (2.42), (2.37), (2.39) ir (14)

, (18)

. (19)

Atsi˛velgdami į krūvininkų koncentracijos ir judrumų iraikas, (17) formulę galime perrayti taip:

. (20)

Ilogaritmavę (20), gauname

. (21)

Pagal (21) grynojo puslaidininkio laidumo logaritmo priklausomybė nuo dyd˛io yra tiesė (5 pav.). Jos polinkio kampas priklauso nuo draud˛iamosios juostos pločio : .

2 u˛duotis

Apskaičiuokime grynojo silicio savitąjį laidumą ir savitąją var˛ą 300 K temperatūroje.

Sprendimas

Grynajame silicyje 300 K temperatūroje cm, cm/(V s), cm/(V s).

Pagal (17) formulę

1/(W m)

W cm).

Tada

W m=2,2 W cm.

Legiruotųjų puslaidininkių laidumą vidutinių temperatūrų srityje lemia pagrindiniai krūvininkai. Tada pagal (10) n ir p puslaidininkių savitieji laidumai ireikiami formulėmis:

, (22)

. (23)

Legiruotojo puslaidininkio elektrinis laidumas priklauso nuo temperatūros ir priemaių koncentracijos. ˇemųjų ir auktųjų temperatūrų srityse (priemaių jonizacijos ir savojo laidumo srityse) krūvininkų koncentracijos daug labiau priklauso nuo temperatūros nei judrumas. Todėl legiruotojo puslaidininkio elektrinio laidumo priklausomybės nuo temperatūros kreivė (6 pav.) panai į elektronų donoriniame puslaidininkyje ir skylių akceptoriniame puslaidininkyje priklausomybes nuo temperatūros (2.13 ir 2.18 pav.). Skirtumas tik tas, kad vidutinių temperatūrų srityje pagrindinių legiruotojo puslaidininkio krūvininkų koncentracija nekinta, o elektrinis laidumas ma˛ėja, kylant temperatūrai. ioje srityje laidumo priklausomybės nuo temperatūros pobūdį nulemia judrumo ma˛ėjimas, didėjant fononinei krūvininkų sklaidai.

Vidutinių temperatūrų srityje pagrindinių krūvininkų koncentracija legiruotame puslaidininkyje lygi priemaių koncentracijai. Todėl, didėjant priemaių koncentracijai, elektrinis puslaidininkio laidumas didėja, nors judrumas, kaip ˛inome, iek tiek ma˛ėja.

Puslaidininkių elektrinis laidumas priklauso ir nuo kitų veiksnių. Toliau aptarsime stipraus elektrinio lauko ir viesos įtaką elektriniam laidumui.

4. Stipraus elektrinio lauko sukeliami reikiniai

Srovės tankis puslaidininkyje tiesikai priklauso nuo elektrinio lauko stiprio, kol elektrinis laukas nėra labai stiprus. Stiprėjant elektriniam laukui, tiesinė priklausomybė (8) sutrinka. Taip atsitinka todėl, kad, sustiprėjus elektriniam laukui, pakinta puslaidininkio elektrinis laidumas. Kai laukas stiprus, srovės tankis ireikiamas formule

(24)

Puslaidininkio elektrinis laidumas, kaip jau isiaikinome, priklauso nuo krūvininkų koncentracijų ir jų judrumų: . Todėl stipraus elektrinio lauko efektai puslaidininkiuose pasireikia dėl krūvininkų judrumo ir koncentracijos kitimo, stiprėjant elektriniam laukui.

4.1. Stipraus lauko įtaka krūvininkų judrumui

Da˛niausiai krūvininkų dreifo greitis elektriniame lauke būna daug ma˛esnis u˛ vidutinį iluminio judėjimo greitį. Jei i sąlyga tenkinama, vidutinis krūvininkų greitis ir jų judrumas nepriklauso nuo elektrinio lauko stiprio.

Stiprėjant elektriniam laukui, dreifo greitis didėja. Kai sąlyga nebetenkinama, didėjant dreifo greičiui, didėja vidutinis krūvininkų greitis. Pagal (13) tai atsiliepia krūvininkų judrumui.

Kai elektrinis laukas greitina krūvininką, elektrinio lauko energija , virsta kinetine krūvininko energija ; čia ir – greitinamo krūvininko kelias ir greitis prie susidūrimą su gardele. Susidurdamas su gardele, krūvininkas praranda greitį, jo kinetinė energija virsta gardelės iluminių virpesių energija. Todėl krūvininko dreifo greitis apytikriai lygus . Taip samprotaudami gauname, kad . Labai stipriame elektriniame lauke . Tada laikydami, kad vyrauja fononinė krūvininkų sklaida (), gauname, kad . Taigi, didėjant elektrinio lauko stipriui, judrumas ma˛ėja (7 pav.).

Jeigu vyrauja jonizuotų priemaių atomų sukelta sklaida, stiprėjant elektriniam laukui, didėja ne tik vidutinis greitis , bet ir skaičius susidūrimų, po kurių krūvininkai praranda kryptingo judėjimo greitį. Kadangi susidūrimų skaičius , pagal (13), didėjant elektrinio lauko stipriui, judrumas didėja ().

Kai elektrinis laukas yra nelabai stiprus, judrumo priklausomybė nuo elektrinio lauko stiprio ireikiama formule:

(25)

čia – judrumas silpname elektriniame lauke, – neomikumo koeficientas. Jei vyrauja fononinė sklaida, būna neigiamas dydis. Tada, stiprėjant elektriniam laukui, judrumas ma˛ėja. Jei vyrauja jonizuotų priemaių sukelta sklaida, tai koeficientas būna teigiamas, ir, stiprėjant elektriniam laukui, judrumas ma˛ėja.

Padidėjus stipriame elektriniame lauke vidutiniam krūvininkų greičiui, padidėja jų vidutinė kinetinė energija. is reikinys vadinamas krūvininkų kaitimu. Krūvininkai, kurių vidutinę kinetinę energiją atitinkanti temperatūra yra didesnė u˛ kristalo gardelės temperatūrą , vadinami kartaisiais krūvininkais.

1958 metais akademiko J. Po˛elos iniciatyva kartųjų krūvininkų tyrimai buvo pradėti Lietuvos mokslų akademijos Fizikos ir matematikos institute. Dabar darbai tęsiami Puslaidininkių fizikos institute.

4.2. Krūvininkų judrumas sudėtiniuose puslaidininkiuose

Laisvojo elektrono energija ireikiama (1.6) formule. Grafikai atvaizduota laisvojo elektrono energijos priklausomybė nuo bangos skaičiaus yra parabolė (1.14 pav.).

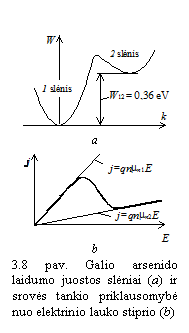
Nagrinėjant laisvuosius kristalo elektronus, vietoj elektrono ramybės masės reikia imti efektinę masę . Elektrono efektinė masė priklauso nuo jo energijos. Todėl priklausomybės pobūdis tampa sudėtingesnis. 8 paveiksle, a, atvaizduota galio arsenido laidumo elektrono minimalios energijos priklausomybė nuo bangos skaičiaus. Kreivė turi du minimumus. Todėl sakoma, kad GaAs laidumo juostoje yra du slėniai, kurių energijos skiriasi dyd˛iu =0,36 eV.

Silpname elektriniame lauke laidumo elektrono vidutinė kinetinė energija yra daug ma˛esnė u˛ , todėl dauguma elektronų yra 1 slėnyje. Jame elektrono efektinė masė , judrumas 8000 cm²/(V s). Taigi elektronų judrumas galio arsenide keletą kartų didesnis nei silicyje. Todėl GaAs leid˛ia padidinti tranzistorių ir kitų puslaidininkinių įtaisų veikimo spartą.

Skylių judrumas galio arsenide daug ma˛esnis nei elektronų. Todėl da˛niausiai naudojamas elektroninio laidumo GaAs.

Kai elektronai yra galio arsenido laidumo juostos 1 slėnyje, jų dreifo greitis ir srovės tankis puslaidininkyje ireikiami formulėmis:

;

čia – laidumo elektronų koncentracija.

Didėjant elektrinio lauko stipriui, srovės tankis didėja (8 pav., b). kartu didėja ir elektronų energija, todėl didėja jų perėjimo į 2 slėnį tikimybė. Kylant elektronams į 2 slėnį, kinta jų sąveikos su kristalo gardele pobūdis, didėja efektinė masė ir ma˛ėja judrumas. Kai elektrinis laukas yra pakankamai stiprus, laidumo elektronai yra antrajame slėnyje. Jame elektrono efektinė masė , judrumas 0,01 m²/(V s), elektronų dreifo greitis ir srovės tankis ireikiami formulėmis

Kadangi, elektronams pereinant į 2 slėnį, jų judrumas smarkiai ma˛ėja, priklausomybės kreivė (8 pav., b) turi sritį, kurioje diferencialinis laidumas yra neigiamas. Todėl galio arsenide, veikiant stipriam elektriniam laukui, gali susi˛adinti mikrobangų virpesiai. į reikinį elektroninio laidumo galio arsenide 1963 metais pastebėjo D˛. B. Ganas (Gunn). Vėliau Gano efektas buvo pritaikytas mikrobangų puslaidininkiniuose įtaisuose – Gano dioduose.

Aptartos galio arsenido savybės būdingos ir kitiems sudėtiniams puslaidininkiams.

4. Stipraus lauko įtaka krūvininkų koncentracijai

Didėjant elektrinio lauko stipriui, gali ˛ymiai pakisti ne tik krūvininkų judrumas, bet ir jų koncentracija. Krūvininkų koncentracija gali padidėti dėl smūginės ir elektrostatinės puslaidininkio atomų jonizacijos.

Veikiant stipriam elektriniam laukui, laisvasis elektronas greitėja, jo kinetinė energija didėja. Įgijęs pakankamai energijos, susidurdamas su gardele, elektronas gali suardyti kovalentinį ryį. Taip atsiranda nauja krūvininkų pora. is reikinys vadinamas smūgine jonizacija.

Elektrinis laukas veikia ne tik laisvuosius krūvininkus. Labai stiprus elektrinis laukas traukia elektronus i kovalentinių ryių. Taigi, veikiant stipriam elektriniam laukui, gali prasidėti elektrostatinė puslaidininkio atomų jonizacija.

Dėl smūginės ar elektrostatinės puslaidininkio atomų jonizacijos padidėjus krūvininkų koncentracijai, padidėja puslaidininkio elektrinis laidumas ir juo tekančios srovės tankis – prasideda puslaidininkio elektrinis pramuimas.

Isamiau pramuimą aptarsime, nagrinėdami reikinius pn sandūrose.

5. Fotolaidumas

Krūvininkų koncentracija puslaidininkyje gali padidėti, jį apvietus. is reikinys vadinamas vidiniu fotoelektriniu reikiniu. Elektrinio laidumo padidėjimą dėl apvietimo lemia fotoelektrinis laidumas arba fotolaidumas.

Da˛niausiai stebimas koncentracinis fotolaidumas. Jo esmę lengvai galima suprasti remiantis juostiniu puslaidininkio modeliu. Jei puslaidininkyje nėra priemaių, o viesos kvanto energija , tai med˛iagai absorbavus viesos kvantą, gali suirti kovalentinis ryys – elektronas gali pakilti i valentinės juostos į laidumo juostą (9 pav., a). Tada laidumo juostoje atsiranda fotoelektronų, o valentinėje juostoje fotoskylių, ir pasireikia savasis fotolaidumas. Jo raudonoji riba apibūdinama ma˛iausiu absorbuotos viesos da˛niu arba ilgiausiu bangos ilgiu:

, (26)

; (27)

čia – viesos greitis.

Kai viesos banga ilgesnė nei , puslaidininkis viesos energijos nesugeria, yra skaidrus, o fotolaidumas nepasireikia.

Priemaiiniuose puslaidininkiuose perteklinius krūvininkus gali sukurti fotonai, kurių . Jei puslaidininkyje yra donorinių priemaių, viesos kvantai gali jonizuoti tų priemaių atomus. Elektronams pakilus i donorinių lygmenų į laidumo juostą (9 pav., b), stebimas priemaiinis fotolaidumas. Jei puslaidininkyje yra akceptorinių priemaių, gali pasireikti skylinis priemaiinis fotolaidumas, susijęs su elektronų uoliais i valentinės juostos į akceptorinius lygmenis (9 pav., c).

Priemaiinis fotolaidumas gali reiktis tik ˛emose temperatūrose, kai ne visi priemaių atomai jonizuoti. Kadangi priemaiinį fotolaidumą gali sukelti ma˛esnės energijos fotonai, jis stebimas veikiant ilgesnėms, ˛emesnio da˛nio viesos bangoms.

I aptarimo seka ivada, kad fotolaidumas priklauso nuo viesos bangos ilgio. Fotolaidumas gali reiktis, kai viesos bangos ilgis yra trumpesnis u˛ krizinį . Trumpėjant bangai, puslaidininkio elektrinis laidumas didėja, pasiekia maksimumą ir pradeda ma˛ėti. Elektrinio laidumo ma˛ėjimas trumpųjų bangų srityje paaikinamas tuo, kad, didėjant da˛niui, didėja fotono energija ir jo sugerties tikimybė. Tada viesa sugeriama ploname paviriniame puslaidininkio sluoksnyje. Jame daug defektų, todėl ma˛as krūvininkų judrumas ir trumpa jų gyvavimo trukmė.

viesa gali turėti įtakos ne tik krūvininkų koncentracijai, bet ir jų judrumui. Fotolaidumas, kurį lemia laisvųjų krūvininkų judrumų pokyčiai, vadinamas judruminiu.

Fotolaidumą selene 1973 metais aptiko V. Smitas (Smith). Fotolaidumu pagrįstas fotorezistorių ir kitų fotoelektrinių įtaisų veikimas. 1951 metais fotolaidumas buvo pradėtas tirti Vilniaus universitete, tyrimų rezultatai naudoti tobulinant elektrografijos techniką.

Belieka pastebėti, kad krūvininkų koncentracija puslaidininkiuose gali padidėti ne tik dėl viesos poveikio. Krūvininkų generaciją gali sukelti ir kitokia elektromagnetinė ar korpuskulinė spinduliuotė – Rentgeno, gama, spinduliai, a b dalelių, protonų, neutronų ir kitų dalelių srautai.

6. Metalų ir lydinių laidumas

Pagal (7) formulę metalo laidumą lemia laisvųjų elektronų koncentracija ir jų judrumas.

ˇinome, kad laisvieji elektronai metale atsiranda, susidarant metalikiesiems ryiams. Tada atomų valentiniai elektronai tampa laisvaisiais elektronais. Jų koncentracija priklauso nuo atomų skaičiaus tūrio vienete ir atomo valentinių elektronų skaičiaus. Ji praktikai nepriklauso nuo temperatūros ir būna 10²²–10²³ cm^– Todėl metalo elektrinio laidumo priklausomybę nuo temperatūros lemia elektronų judrumas.

Nagrinėjant elektronų judrumą metale, reikia nepamirti, kad elektronų koncentracija metale didelė. Jie u˛ima energijos lygmenis, esančius ˛emiau Fermio lygmens. Esantieji vir Fermio lygmens energijos lygmenys laisvi.

Metaluose elektrinis laukas silpnas. Silpnas laukas gali pakeisti energiją tik tų elektronų, kurie yra arti laisvų lygmenų. Todėl metalo laisvųjų elektronų dreifo greitį ir judrumą lemia elektronai, u˛imantieji energijos lygmenis prie pat Fermio lygmens. Judrumas ireikiamas formule, panaia į (13):

; (28)

čia – u˛imančio Fermio lygmenį elektrono vidutinis laisvasis kelias, – skaičius susidūrimų, po kurių is elektronas praranda kryptingo judėjimo greitį, – vidutinis minėto elektrono greitis.

Remdamiesi (28) formule, aptarkime, kaip metalo elektronų judrumas ir savitasis laidumas priklauso nuo temperatūros ir priemaių koncentracijos.

Jei elektrinis laukas silpnas, tai elektronų dreifo greitis būna ma˛as. Todėl, skaičiuojant vidutinį greitį , dreifo greičio galima nepaisyti ir laikyti, kad elektrono vidutinis greitis apytikriai lygus iluminio judėjimo greičiui . Pagal (2.19) absoliučiojo nulio temperatūroje metalo elektronų Fermio energija priklauso nuo laisvųjų elektronų koncentracijos. Kylant temperatūrai, elektronų koncentracija metale ir Fermio lygmens padėtis beveik nekinta. Todėl galima laikyti, kad u˛imančių Fermio lygmenį elektronų vidutinis greitis nekinta, kylant temperatūrai.

Metalo elektronų vidutinį laisvąjį kelią nulemia elektronų susidūrimai su gardelės defektais. Jei vyrauja fononinė elektronų sklaida, tai , o . Tada pagal (28) ir (7) grynojo metalo elektronų judrumas ir savitasis laidumas atvirkčiai proporcingi temperatūrai: , . Grynojo metalo savitoji var˛a, kylant temperatūrai, didėja:

. (29)

ią ivadą, kaip ˛inoma, patvirtina eksperimentai. Pagal eksperimentinių tyrimų rezultatus

; (30)

čia – var˛os temperatūrinis koeficientas, ir – savitoji var˛a temperatūrose ir .

Paprastai net gryniausiame metale esti priemaių. Todėl ˛emų temperatūrų srityje elektronų vidutinį laisvąjį kelią riboja tik susidūrimai su priemaių atomais. Tada ne tik bei , bet ir nepriklauso nuo temperatūros. Todėl nuo temperatūros nepriklauso nei krūvininkų judrumas, nei metalo savitasis laidumas, nei jo savitoji var˛a.

Bet kurioje temperatūroje metalo savitąją var˛ą sudaro abi dedamosios ir , atsirandančios dėl priemaiinės ir fononinės elektronų sklaidų:

. (31)

10 paveiksle atvaizduotas metalo savitosios var˛os priklausomybės nuo temperatūros grafikas. Pagal (31) formulę ir 10 paveikslą absoliučiojo nulio temperatūroje lieka tik savitosios var˛os dedamoji . Todėl ji dar vadinama liekamąja var˛a.

Didėjant priemaių koncentracijai, ir didėja. Todėl metalų lydinių, kuriuose vieno metalo atomai yra priemaia kito metalo gardelėje, savitoji var˛a būna didesnė u˛ grynųjų metalų savitąsias var˛as. į teiginį galima iliustruoti tokiu pavyzd˛iu. Sidabro savitoji var˛a yra ma˛esnė nei aliuminio. Tačiau į aliuminį įmaiius sidabro, jo savitoji var˛a ne suma˛ėja, o padidėja. Lydinio, kuriame yra apie 90 % sidabro ir 10 % aliuminio, savitoji var˛a 300 K temperatūroje yra 15 kartų didesnė u˛ aliuminio savitąją var˛ą ir 30 kartų didesnė u˛ sidabro savitąją var˛ą. Lydinių var˛a yra didelė todėl, kad kristalinės gardelės defektai labai suma˛ina elektronų laisvąjį kelią ir judrumą.

Kuo daugiau reikiasi priemaiinė sklaida, tuo ma˛iau var˛a priklauso nuo temperatūros. Todėl metalų lydinių temperatūriniai var˛os koeficientai būna daug ma˛esni u˛ grynųjų metalų temperatūrinius var˛os koeficientus.

3 u˛duotis

Kaip ir kiek kartų pakistų grynojo silicio, n silicio ir vario bandinių var˛os kylant temperatūrai nuo 300 iki 340 K?

Sprendimas

Var˛a atvirkčiai proporcinga laidumui. Taigi

Grynojo puslaidininkio savitasis laidumas ireikiamas (20) formule. Tada

Legiruotojo puslaidininkio pagrindinių krūvininkų koncentracija vidutinių temperatūrų srityje nekinta. Savitojo laidumo kitimą lemia judrumo kitimas. Tada

Pagal 6 paveikslą ir (15) formulę . Tada legiruotojo puslaidininkio

Varis yra metalas. Pagal (29) formulę

Pagal ˛inynus vario temperatūrinis var˛os koeficientas 1/K. ˇinodami temperatūrinį var˛os koeficientą ir taikydami (30) formulę, gautume, kad

Taigi, kylant temperatūrai, grynojo silicio bandinio var˛a sparčiai ma˛ėja, legiruotojo silicio ir vario bandinių var˛os didėja.

7. Superlaidumas

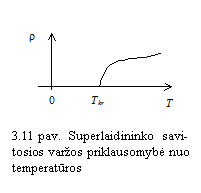
Superlaidumo reikinį 1911 metais pastebėjo H. Kamerlingas Onesas (Kamerling Onnes), tirdamas gyvsidabrio liekamąją var˛ą. Superlaidumas pasireikia tuo, kad laidininko elektrinė var˛a suma˛ėja beveik iki nulio, kai to laidininko temperatūra tampa ˛emesnė u˛ jam būdingą krizinę (superlaidaus virsmo) temperatūrą (11 pav.). Gyvsidabrio =4,2 K.

Superlaidumo mikroskopinę teoriją 1957 metais sukūrė D˛. Bardynas (Bardeen), L. Kūperis (Cooper) ir D˛. ryferis (Schrieffer). Pagal ią teoriją, svarbiausia superlaidumą sukelianti prie˛astis yra elektronų ir kristalinės gardelės sąveika. Dėl ios sąveikos laisvieji elektronai deformuoja gardelę. Prie jų priartėja teigiamieji jonai. Elektronas ir jį supantys jonai sudaro teigiamai įelektrintą visumą, pritraukiančią antrą elektroną. Taip susidaro elektronų poros, vadinamos Kūperio poromis. Atstumas tarp Kūperio poros elektronų yra apie 10^–6 m. Kūperio poras sudaro elektronai, kurių sukiniai yra prieingų ˛enklų. Todėl Kūperio poros sukinys lygus nuliui ir Kūperio poros pasi˛ymi bozonų savybėmis. Vieną ir tą patį energijos lygmenį gali u˛imti bet koks Kūperio porų skaičius.

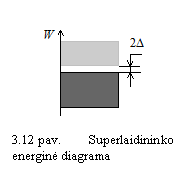
Elektronams jungiantis į Kūperio poras, jų bendra energija suma˛ėja, Tarp u˛pildytų ir neu˛imtų energijos lygmenų atsiranda draud˛iamosios energijos plyys (12 pav.). Jis esti kelių milielektronvoltų pločio.

ˇemų temperatūrų srityje gardelės iluminių virpesių energijos nepakanka Kūperio poroms suardyti, todėl jų sklaida nepasireikia. Turėdamos tą pačią energiją, Kūperio poros gali nesąveikaudamos su gardele tvarkingai judėti kristale. Kadangi gardelėje nekyla pasiprieinimo Kūperio porų judėjimui, tai superlaidininko laidumas esti labai didelis, jo savitoji var˛a praktikai lygi nuliui. Jei superlaidininko ˛iede su˛adinama srovė, ji teka nesilpnėdama.

Superlaidumas inyksta, kai superlaidininko temperatūra tampa auktesnė u˛ krizinę arba kai superlaidininko temperatūra ˛emesnė u˛ krizinę, bet jis yra stipresniame u˛ krizinį magnetiniame lauke, arba kai juo teka srovė, stipresnė u˛ krizinę srovę.

Superlaidininkas pasi˛ymi idealaus diamagnetiko savybėmis. Silpnesnis u˛ krizinį iorinis magnetinis laukas neįsiskverbia į superlaidininką. is reikinys vadinamas Meisnerio (Meissner) efektu.

Superlaidumas buvo pastebėtas daugiau kaip dviejuose tūkstančiuose grynųjų med˛iagų ir junginių, tačiau jų superlaidaus virsmo temperatūra buvo ˛emesnė nei 24 K. 1986 metais IBM firmos veicarijoje mokslininkams J. Bednorcui (Bednorz) ir K. Miuleriui (Muller) pavyko sukurti keramiką, kurios superlaidaus virsmo temperatūra buvo apie 35 K. Vėliau JAV mokslininkai i itrio, bario ir vario oksidų su priedais susintetino keramiką, kuri tampa superlaidi 92 K temperatūroje, auktesnėje u˛ skysto azoto virimo temperatūrą (77 K). Yra optimistinių prognozių, kad pavyks sukurti med˛iagas, kurios būtų superlaid˛ios net normalioje temperatūroje.

Superlaidumo reikinį numatoma plačiai panaudoti energetikoje, elektrotechnikoje, elektronikoje, skaičiavimo ir matavimo technikoje. Paprasčiausias krioelektronikos – ˛emųjų temperatūrų elektronikos – įtaisas yra kriotronas. Kry˛minio plonasluoksnio kriotrono sandara atvaizduota 13 paveiksle. Jis sudarytas i valdomosios alavo ynos, dielektriko sluoksnio ir valdymo ynos. Kriotrono veikimas pagrįstas staigiu valdomosios ynos var˛os pokyčiu pakitus magnetiniam laukui, kurį sukuria srovė, tekanti valdymo yna. Kriotronas yra ma˛ų matmenų, vartoja ma˛ai energijos. Jo veikimo sparta yra labai didelė: persijungimo trukmė yra tik pikosekund˛ių eilės.

8. D˛ozefsono efektai

Superlaidininko var˛a labai ma˛a. Todėl, tekant superlaidininku srovei, jame nepastebimas įtampos kritimas.

Perpjaukime superlaidininko bandinį į dvi dalis ir įterpkime tarp jų ploną (kelių nanometrų storio) dielektriko sluoksnį. Gautasis darinys (14 pav., a) vadinamas D˛ozefsono sandūra. Tirdamas jos savybes, B. D˛osefsonas (Josephson) 1962 metais numatė, o P. V. Andersonas (Anderson) ir D˛. M. Rovelis (Rowell) 1963 metais atrado du reikinius.

Jei per D˛ozefsono sandūrą teka nuolatinė srovė, ne stipresnė u˛ tam tikrą krizinę , tai įtampa sandūroje nekrinta. is reikinys vadinamas stacionariuoju D˛ozefsono efektu.

Srovės stipriui virijus krizinę reikmę, D˛ozefsono sandūroje krinta įtampa (15 pav.), grandinėje atsiranda kintamoji srovės dedamoji, sandūra spinduliuoja elektromagnetines bangas. is reikinys vadinamas nestacionariuoju D˛ozefsono efektu.

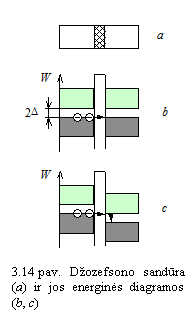Stacionarusis D˛ozefsono efektas paaikinamas tuo, kad per D˛ozefsono sandūrą teka tunelinė srovė. Mikrodalelėms (iuo atveju – Kūperio poroms) tuneliniu būdu skverbiantis per ploną dielektriko sluoksnį (14 pav., b), jų energija nekinta. Todėl įtampa D˛osefsono sandūroje nekrinta.

Tunelinė srovė per D˛ozefsono sandūrą ireikiama formule

;

čia – banginių funkcijų, apraančių Kūperio poras abiejose barjero pusėse, fazių skirtumas.

Sakykime, kad D˛ozefsono sandūroje krinta įtampa . Tada Kūperio porų energijų skirtumas abiejose dielektriko sluoksnio pusėse yra lygus ; čia – Kūperio poros krūvis. į energijų skirtumą atitinka de Broilio bangų da˛nių skirtumas ir banginių funkcijų fazių skirtumas

Minimalus įtampos kritimas D˛ozefsono sandūroje atitinka draud˛iamosios energijos plyio plotį, nes . į ryį iliustruoja 14 paveikslas, c, kuriame atvaizduota D˛ozefsono sandūros energinė diagrama.

Kai pirmosios superlaidininko dalies energijos lygmenys yra aukčiau u˛ antrosios dalies energijos lygmenis, elektronai i u˛imtų lygmenų gali pereiti į tučius lygmenis, esančius vir draud˛iamosios energijos plyio (14 pav., c). Po to elektronai jungiasi į Kūperio poras ir grį˛ta į lygmenis, esančius ˛emiau draud˛iamojo plyio. Atsipalaiduojanti energija ispinduliuojama elektromagnetiniais virpesiais.

Taikant D˛ozefsono efektus, sukurti kvantinės elektronikos elementai (kriosarai, skvidai), loginės schemos ir integriniai grandynai. Visi D˛ozefsono efektais pagrįsti kvantinės elektronikos įtaisai pasi˛ymi labai didele veikimo sparta ir vartoja nedaug energijos.

9. Holo efektas

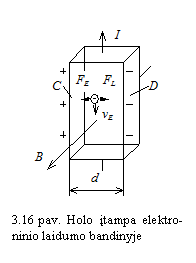
Sakykime, kad metalo arba puslaidininkio bandinys (16 pav.) yra magnetiniame lauke. Magnetinės indukcijos kryptis statmena bandiniu tekančios srovės krypčiai. Tada tarp bandinio sienelių C ir D atsiranda potencialų skirtumas . į reikinį 1879 metais atrado E. H. Holas (Hall). Potencialų skirtumas vadinamas Holo įtampa.

Sakykime, kad pagrindiniai bandinio krūvininkai yra elektronai. Judantį magnetiniame lauke dreifo greičiu elektroną, kurio krūvis , veikia Lorenco (Lorentz) jėga

ios jėgos kryptį galima rasti pagal kairiosios rankos taisyklę. Kai greičio ir magnetinės indukcijos vektoriai statmeni, jėgos modulis ireikiamas formule

. (33)

Lorenco jėgos veikiami elektronai nukrypsta link sienelės D. Prie sienelės C lieka nesukompensuoti teigiamieji jonai. Tarp sienelių C ir D atsiranda elektrinis laukas, kurio stipris

; (34)

čia – bandinio matmuo (16 pav.).

Elektriniame lauke, kurio stipris , elektroną veikia jėga, kurios modulis

. (35)

Pusiausvyros sąlygomis jėgos ir atsveria viena kitą. Jų moduliai lygūs. Todėl galime rayti:

. (36)

Tada

. (37)

Bandiniu tekančios srovės tankis ireikiamas formule

. (38)

Tada, remdamiesi (34), ir (36) – (38) formulėmis, gauname:

; (39)

čia – Holo konstanta.

Kai pagrindiniai bandinio krūvininkai yra elektronai, savitasis laidumas ireikiamas formule . Tada

. (40)

Vadinasi, imatavus Holo konstantą ir savitąjį laidumą , taikant (40) formulę, galima apskaičiuoti elektronų judrumą.

Nesunku taip pat įsitikinti, kad Holo įtampos polikumas ir Holo konstantos ˛enklas priklauso nuo pagrindinių krūvininkų tipo. Vadinasi, pagal Holo įtampos polikumą galima nustatyti pagrindinių krūvininkų ˛enklą ir puslaidininkio laidumo tipą.

Holo reikiniu pagrįsti puslaidininkiniai įtaisai – Holo keitikliai – naudojami daugelyje mokslo ir technikos sričių. Jie taikomi srovės stipriui, magnetinei indukcijai, galiai matuoti, signalams apdoroti ir kitiems tikslams.

10. Krūvininkų difuzija

Neveikiant elektriniam laukui, krūvininkai gali kryptingai judėti dėl nevienalytės koncentracijos. Jeigu krūvininkų koncentracija tam tikra kryptimi ma˛ėja, tai pasireikia jų kryptingas slinkimas koncentracijos ma˛ėjimo kryptimi. Dalelių skverbimasis koncentracijos ma˛ėjimo kryptimi vadinamas difuzija.

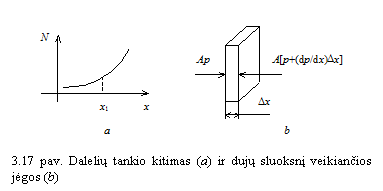
Siekdami isiaikinti, kaip vyksta difuzija, prad˛ioje nagrinėkime i neutralių dalelių sudarytas dujas. Sakykime, kad dalelių koncentracija didėja koordinatės kryptimi (17 pav., a). Koncentracijos kitimo greitis apibūdinamas koncentracijos gradientu. Kai dalelių koncentracija priklauso tik nuo vienos koordinatės , jų koncentracijos gradientas ireikiamas formule:

. (41)

Įsivaizduokime statmeną aiai ploktumą, . Jeigu dalelių koncentracijos gradientas nelygus nuliui, tai dalelių tankis vienoje ploktumos pusėje didesnis nei kitoje. Kadangi, kai 0, dalelės chaotikai juda, daugiau jų prasiskverbia per tariamą ploktumą i tos pusės, kur didesnis tankis. Taigi pasireikia dalelių difuzija koncentracijos ma˛ėjimo kryptimi – i srities, kur slėgis didesnis, į sritį, kur slėgis ma˛esnis.

Imkime ploną dujų sluoksnį, statmeną aiai (17 pav., b). Jeigu jo plotas yra , tai i kairės tą sluoksnį veikia jėga , i deinės – jėga ; čia – slėgis, – sluoksnio storis. Tada atstojamoji jėga ireikiama formule:

. (42)

Nagrinėjamame sluoksnyje yra dalelių. Tada vieną dalelę veikianti jėga lygi

. (43)

Tarp dujų dalelių koncentracijos ir slėgio, kaip ˛inome, yra ryys:

. (44)

Įraę (43) į (42), gauname:

(45)

Taigi dalelių difuzijos varomoji jėga proporcinga temperatūrai ir dalelių koncentracijos gradientui.

Veikiant difuzijos varomajai jėgai, elektronai kietajame kūne judėtų panaiai kaip veikiami elektrinio lauko sukeltos jėgos. Jie judėtų chaotikai, susidurdami su gardele ir kartu slinktų koncentracijos ma˛ėjimo kryptimi.

Kai veikia elektrinis laukas ir jėga , elektronas įgyja dreifo greitį, kuris proporcingas jėgai :

. (46)

Kai veikia difuzijos varomoji jėga, elektrono difuzijos greitis proporcingas jėgai , ireikiamai (45) formule:

; (47)

čia – elektronų koncentracija, – jų difuzijos koeficientas.

Pagal (47) elektronų difuzijos koeficientas ireikiamas formule:

. (48)

ˇinodami elektronų difuzijos greitį, galime rasti elektroninės difuzinės srovės tankį:

. (49)

Nagrinėdami skyles, gautume analogikas skylių dreifo greičio, difuzijos koeficiento ir skylinės difuzinės srovės iraikas:

, (50)

, (51)

. (52)

Verta atkreipti dėmesį, kad elektroninės difuzinės srovės kryptis sutampa su elektronų koncentracijos didėjimo kryptimi. Skylinės difuzinės srovės kryptis prieinga skylių koncentracijos didėjimo krypčiai.

Kadangi krūvininkų judėjimas kietajame kūne, veikiant elektriniam laukui, yra panaus į jų judėjimą dėl koncentracijos gradiento, krūvininkų difuzijos koeficientai ir judrumai yra susieti. Pagal (48) ir (51) formules

. (53)

Pastarieji sąryiai vadinami Einteino sąryiais.

11. Puslaidininkiuose tekančios srovės

Bendruoju atveju krūvininkų koncentracijos puslaidininkyje gali būti nevienalytės ir dar gali veikti elektrinis laukas. Tada elektroninė ir skylinė srovės yra sudarytos i dreifinės ir difuzinės dedamųjų.

Pagal (8) ir (49) elektroninės srovės tankis ireikiamas formule:

. (54)

Skylinės srovės tankis

. (55)

Pilnutinės srovės tankis ireikiamas formule:

. (56)

Taigi elektros srovė puslaidininkyje sudaryta i elektroninės dreifinės, elektroninės difuzinės, skylinės dreifinės ir skylinės difuzinės dedamųjų.

12. Ivados

Sukūrus kietajame kūne elektrinį lauką, kartu su chaotikuoju krūvininkų judėjimu vyksta jų kryptingas slinkimas – dreifas. Dreifo greitis proporcingas elektrinio lauko stipriui ir krūvininkų judrumui.

Kietojo kūno savitąjį elektrinį laidumą lemia krūvininkų koncentracija ir judrumas: .

Krūvininkų judrumą kietajame kūne riboja jų susidūrimai su gardelės defektais. Gardelės defektus sukelia jos atomų iluminiai virpesiai ir priemaių atomai. Todėl puslaidininkių krūvininkų judrumas priklauso nuo temperatūros ir priemaių koncentracijos.

Grynojo puslaidininkio elektrinis laidumas labai priklauso nuo draud˛iamosios juostos pločio ir temperatūros. Priklausomybių pobūdį lemia krūvininkų koncentracija. Kuo platesnė grynojo puslaidininkio draud˛iamoji juosta, tuo ma˛esnis jo savitasis laidumas. Kylant temperatūrai, grynojo puslaidininkio laidumas sparčiai didėja.

Priemaiinio puslaidininkio savitasis laidumas didesnis nei grynojo ir priklauso nuo temperatūros ir priemaių koncentracijos. 300 K temperatūros aplinkoje, kylant temperatūrai, priemaiinio puslaidininkio laidumas ma˛ėja, nes krūvininkų koncentracija nekinta, o judrumas, kylant temperatūrai, ma˛ėja dėl fononinės krūvininkų sklaidos.

Galio arsenido ir kitų sudėtinių puslaidininkių laidumo juostoje yra du slėniai. Elektronams kylant į auktesnį slėnį, ma˛ėja jų judrumas, ir gali pasireikti puslaidininkio neigiamas diferencialinis laidumas.

Labai stiprus elektrinis laukas turi įtakos krūvininkų judrumui ir koncentracijai. Jis gali sukelti smūginę ar elektrostatinę puslaidininkio atomų jonizaciją. Yrant kovalentiniams ryiams gali labai padidėti krūvininkų koncentracija ir prasidėti puslaidininkio elektrinis pramuimas.

Kai krūvininkų koncentracija nevienalytė, pasireikia jų difuzija – slinkimas koncentracijos ma˛ėjimo kryptimi. Difuzinės srovės tankis proporcingas krūvininkų difuzijos koeficientui ir jų koncentracijos gradientui.

Kai veikia elektrinis laukas ir krūvininkų koncentracija yra nevienalytė, puslaidininkyje tekanti elektros srovė sudaryta i keturių dedamųjų: elektroninės dreifinės, elektroninės difuzinės, skylinės dreifinės ir skylinės difuzinės srovių.

1 Kontroliniai klausimai ir u˛duotys

Apibūdinkite elektronų judėjimą kietajame kūne, kai jame sudarytas elektrinis laukas.

Iveskite elektronų dreifo greičio iraiką. Aptarkite, nuo ko dreifo greitis priklauso.

Paaikinkite krūvininkų judrumo prasmę.

Iveskite bendriausią krūvininkų judrumo iraiką. Aptarkite, nuo ko judrumas priklauso.

Iveskite kietojo kūno savitojo elektrinio laidumo bendriausią iraiką. Aptarkite, kas lemia savitąjį laidumą.

Kokie reikiniai riboja krūvininkų judrumą puslaidininkyje?

Nuo ko, kaip ir kodėl priklauso krūvininkų judrumas grynajame puslaidininkyje?

Aptarkite krūvininkų judrumą priemaiiniame puslaidininkyje.

Nuo ko, kaip ir kodėl priklauso grynojo puslaidininkio savitasis elektrinis laidumas?

Kodėl priemaiinio puslaidininkio elektrinis laidumas vidutinių temperatūrų srityje ma˛ėja, kylant temperatūrai?

Apskaičiuokite grynojo puslaidininkio savitąjį laidumą, kai cm, cm/(V s), cm/(V s). Koks būtų io puslaidininkio savitasis laidumas, jį legiravus donorinėmis priemaiomis, kurių koncentracija =3,5 cm

Ats.: 1,5 , 7,8 W cm.

Kaip ir kiek kartų pakistų grynojo silicio ir p silicio laidumai, temperatūrai kylant nuo 20 iki 40 ^oC?

Ats.: 4; 0,91.

Nurodykite stipraus lauko efektų puslaidininkyje prie˛astis.

Koks yra stipraus lauko kriterijus?

Elektronų judrumas silicyje 300 K temperatūroje – 0,13 m/(V s). Kokio stiprio elektriniame lauke elektronų dreifo greitis pasiektų vidutinį kvadratinį iluminio judėjimo greitį?

Ats.: 9 V/m.

Kodėl gali pasireikti galio arsenido neigiama diferencialinė var˛a?

Kokia yra Gano efekto esmė?

Aptarkite elektrinio lauko įtaką krūvininkų koncentracijai puslaidininkyje.

Ką vadina fotolaidumu?

Paaikinkite savojo fotolaidumo ir priemaiinio fotolaidumo mechanizmus.

Regimosios viesos bangos ilgių spektras yra nuo 380 iki 780 nm. Koks turi būti puslaidininkio draud˛iamosios juostos plotis, kad puslaidininkis tiktų regimosios viesos detektoriams?

Ats.: 1,59 eV.

Kaip ir kodėl puslaidininkio fotolaidumas priklauso nuo viesos bangos ilgio?

Kas lemia metalo elektronų judrumą? Kaip metalo elektronų judrumas ir metalo savitoji var˛a priklauso nuo temperatūros?

Kodėl pasireikia metalo liekamoji var˛a?

Koks yra superlaidumo mechanizmas?

Kokia yra D˛ozefsono efektų esmė?

Legiruoto silicio bandinio savitoji var˛a – 9,27 W m, jo Holo konstanta – 3,84 m/C. Raskite pagrindinių krūvininkų koncentraciją ir judrumą.

Ats.: 1,6 m 0,04 m/Vs.

Kvadratinio skerspjūvio n germanio bandiniu, kurio skerspjūvio plotas – 4 mm, teka 10 mA stiprumo srovė. Veikiant 0,1 T skersiniam magnetiniam laukui, gaunama 1 mV Holo įtampa. Raskite bandinio Holo konstantą ir elektronų koncentraciją.

Ats.: 0,002 m/C, 3,1 m

Kokiomis sąlygomis vyksta dalelių difuzija? Kas yra difuzijos varomoji jėga? Nuo ko ir kaip ji priklauso?

Iveskite difunduojančio krūvininko greičio iraiką.

U˛raykite difuzinės srovės tankio iraiką. Aptarkite, nuo ko ir kaip i srovė priklauso.

I kokių dedamųjų sudaryta puslaidininkyje tekanti srovė?

3sk_r1.doc 2001.05.14 14:24 2001.10.18 08:10 2001.11.10

Politica de confidentialitate | Termeni si conditii de utilizare

DISTRIBUIE DOCUMENTUL

Vizualizari: 2525
Importanta:

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Distribuie URL
https://www.scrigroup.com/limba/lituaniana/255/KIETJ-KN-ELEKTRINIS-LAIDUMAS94149.php

Adauga cod HTML in site
<a href="https://www.scrigroup.com/limba/lituaniana/255/KIETJ-KN-ELEKTRINIS-LAIDUMAS94149.php" target="_blank" title=" - https://www.scrigroup.com/limba/lituaniana/255/KIETJ-KN-ELEKTRINIS-LAIDUMAS94149.php">KIETŲJŲ KŪNŲ ELEKTRINIS LAIDUMAS</a>

KIETŲJŲ KŪNŲ ELEKTRINIS LAIDUMAS

elektra

DOCUMENTE SIMILARE

KIETŲJŲ KŪNŲ ELEKTRINIS LAIDUMAS

1. Krūvininkų dreifas ir relaksacija

2. Puslaidininkių krūvininkų judrumas

Puslaidininkių elektrinis laidumas

4. Stipraus elektrinio lauko sukeliami reikiniai

4.1. Stipraus lauko įtaka krūvininkų judrumui

4.2. Krūvininkų judrumas sudėtiniuose puslaidininkiuose

4. Stipraus lauko įtaka krūvininkų koncentracijai

5. Fotolaidumas

6. Metalų ir lydinių laidumas

7. Superlaidumas

8. D˛ozefsono efektai

9. Holo efektas

10. Krūvininkų difuzija

11. Puslaidininkiuose tekančios srovės

12. Ivados

1 Kontroliniai klausimai ir u˛duotys

DISTRIBUIE DOCUMENTUL

Comenteaza documentul:

4. Stipraus elektrinio lauko sukeliami reikiniai

12. Ivados