CATEGORII DOCUMENTE
Afaceri Calculatoare Casa masina Didactica pedagogie Diverse Educatie Finante Geografie Istorie & politica Legislatie Limba Management Sanatate Tehnologie

Bulgara	Ceha slovaca	Croata	Engleza	Estona	Finlandeza	Franceza
Germana	Italiana	Letona	Lituaniana	Maghiara	Olandeza	Poloneza
Sarba	Slovena	Spaniola	Suedeza	Turca	Ucraineana

įstatymai	įvairių	Apskaitos	Architektūra	Biografija	Biologija	Botanika	Chemija
Ekologija	Ekonomika	Elektra	Finansai	Fizinis	Geografija	Istorija	Karjeros
Kompiuteriai	Kultūra	Literatūra	Matematika	Medicina	Politika	Prekyba	Psichologija
Receptus	Sociologija	Technika	Teisė	Turizmas	Valdymas	vietimas

NEVIENALYČIAI PUSLAIDININKIAI. pn SANDŪROS

elektra

+ Font mai mare | - Font mai mic


DOCUMENTE SIMILARE

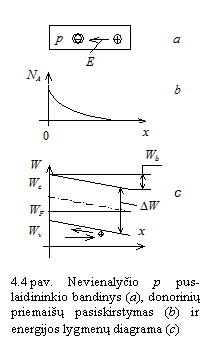
NEVIENALYČIAI PUSLAIDININKIAI. pn SANDŪROS

Nevienalyčiais vadinami puslaidininkiai, kurių savybės kinta bent vienos koordinatės kryptimi. Nevienalyčio puslaidininkio kristale gali būti skirtingo laidumo tipo sričių. Pereinamasis sluoksnis tarp puslaidininkio monokristalo p ir n sričių vadinamas skyline elektronine, arba pn sandūra.

iame skyriuje aptarsime reikinius nevienalyčiuose puslaidininkiuose ir pn sandūrose ir ių puslaidininkių bei pn sandūrų savybes.

1. Nevienalytis puslaidininkis

Tarkime, kad puslaidininkio bandinyje donorinės priemaios koncentracija kinta iilgai koordinatės (1 pav.). Kambario temperatūroje donorai yra jonizuoti, todėl elektronų koncentracija priklauso nuo koordinatės .

Dėl nevienalytės koncentracijos vyksta elektronų difuzija kryptimi. Difunduodami elektronai palieka nesukompensuotus donorų jonus. Taip nevienalyčiame puslaidininkyje atsiranda vidinis elektrinis laukas (2 pav.). Elektrinis laukas sukelia krūvininkų dreifą.

Pusiausvyros sąlygomis elektroninės ir skylinės srovių tankiai bandinyje turi būti lygūs nuliui. Taikydami (3.54) ir (3.55) formules, galime rayti:

, (1)

. (2)

I ių formulių gauname:

, (3)

. (4)

Atsi˛velgę į tai, kad , galime įsitikinti, kad (3) ir (4) iraikos yra tapatingos.

Sakykime, kad elektronų koncentracija bandinyje kinta eksponentiniu dėsniu:

(5)

Tada pagal (3)

. (6)

Taigi, kai krūvininkų koncentracija kinta eksponentiniu dėsniu, elektrinio lauko stipris bandinyje yra pastovus, nepriklauso nuo koordinatės.

ˇinodami elektrinio lauko stiprį, galime rasti potencialo pasiskirstymą bandinyje, nes

. (7)

Pagal (7)

. (8)

Įraę į (8) elektrinio lauko stiprio iraikas (3) ir (4), gauname:

. (9)

Integruokime nuo tako , kurio potencialas ir kurio aplinkoje krūvininkų koncentracijos ir , iki tako , kurio potencialas ir kurio aplinkoje krūvininkų koncentracijos ir :

. (10)

Atlikę integravimą, gauname potencialų skirtumo tarp paminėtų bandinio takų iraiką:

. (11)

Pagal (11) potencialų skirtumas tarp bandinio takų priklauso tik nuo krūvininkų koncentracijų tų takų aplinkose.

Taigi nevienalyčiame puslaidininkyje vyksta krūvininkų difuzija jų koncentracijų ma˛ėjimo kryptimi ir atsiranda vidinis elektrinis laukas, sukeliantis krūvininkų dreifą. Dėl krūvininkų koncentracijų kitimo bandinyje kinta elektrinis potencialas. Potencialų skirtumą tarp bandinio takų lemia krūvininkų (elektronų arba skylių) koncentracijų santykis.

Kaip jau isiaikinome, apie puslaidininkio savybes galima spręsti pagal jo energijos lygmenų diagramą. Taigi sudarykime nevienalyčių n ir p puslaidininkių energijos lygmenų diagramas. į u˛davinį nesunku atlikti remiantis jau įgytomis ˛iniomis:

Pusiausvyros būsenoje Fermio lygmuo bandinyje pastovus, nepriklauso nuo koordinatės.

Kai priemaių koncentracija lygi nuliui (puslaidininkis – grynas), Fermio lygmuo yra ties draud˛iamosios juostos viduriu.

n puslaidininkyje Fermio lygmuo yra vir draud˛iamosios juostos vidurio.

p puslaidininkyje Fermio lygmuo yra ˛emiau draud˛iamosios juostos vidurio.

Remiantis iomis ˛iniomis sudarytos nevienalyčių puslaidininkių energijos lygmenų diagramos atvaizduotos 3 ir 4 paveiksluose. I jų matyti, kad nevienalyčiuose puslaidininkiuose atsiranda potencialo barjerai. Jeigu nesikeičia puslaidininkio laidumo tipas, potencialo barjero auktis yra ne didesnis nei .

Jeigu bandinio takų potencialai nevienodi, tai elektronų potencinės energijos ir iuose takuose yra nevienodos:

(12)

Tada

. (13)

Jeigu potencialo barjero auktis nevirija , tai kontaktinis potencialų skirtumas nevienalyčio tam tikro laidumo tipo puslaidininkio bandinyje tenkina sąlygą

. (14)

Silicio draud˛iamosios juostos plotis yra 1,1 eV. Taigi 0,55 eV.

Pagal 3 paveikslą, c, ir 4 paveikslą, c, nevienalyčio puslaidininkio krūvininkai (laidumo juostos elektronai ir valentinės juostos skylės), difunduodami koncentracijos ma˛ėjimo kryptimi, sutinka potencialo barjerus, atsirandančius dėl vidinio elektrinio lauko bandinyje. Krūvininkai, kuriems barjeras auktas, atsispindi ir pakeičia judėjimo kryptį.

Nagrinėjant valentinės juostos skylių judėjimą būtina prisiminti, kad skylė yra tarsi dujų burbuliukas skystyje ir jos energija didesnė, jei ji u˛ima ˛emesnį valentinės juostos lygmenį. Skylės nuotolis nuo valentinės juostos viraus atitinka skylės kinetinę energiją.

1 u˛duotis

Silicio dreifinio npn tranzistoriaus bazėje priemaių koncentracija kinta eksponentiniu dėsniu. Bazės storis – 1 mm. Įvertinkime elektrinio lauko stiprį tranzistoriaus bazėje.

Sprendimas

Tranzistoriaus bazė yra p puslaidininkio sluoksnis. Tam tikro laidumo tipo sluoksnyje kontaktinis potencialų skirtumas yra ne didesnis nei . Jeigu puslaidininkis silicis, tai 0,55 V. Sakykime, kad . Tada

2. pn sandūra

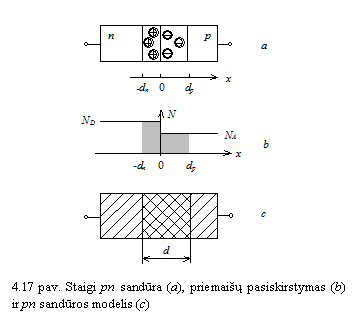
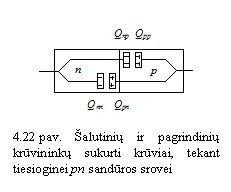
Puslaidininkio bandinyje galima sudaryti skirtingo laidumo tipo sritis. Tarp puslaidininkinio darinio p ir n sričių susidaro pereinamasis sluoksnis, vadinamas pn sandūra. pn sandūros būna staigios ir tolydinės, simetrinės ir nesimetrinės. Staigiojoje pn sandūroje priemaių koncentracijos kinta uoliu, tolydinėje – palaipsniui. pn sandūra yra simetrinė, kai donorinių priemaių koncentracija n srityje yra tokia pat kaip akceptorinių priemaių koncentracija p srityje. Jeigu priemaių koncentracijos nevienodos, susidaro nesimetrinė pn sandūra.

Nagrinėkime staigiąją simetrinę pn sandūrą silicio monokristalo luste (5 pav., a), į kurio kairiąją pusę įterpta akceptorinių priemaių (jų koncentracija ), į deiniąją pusę – donorinių priemaių (jų koncentracija – ). Sakykime, kad 10¹⁶/cm³.

Vidutinių temperatūrų srityje visi priemaių atomai yra jonizuoti. Todėl kairiojoje darinio pusėje skylių koncentracija 10¹⁶cm^–3. Elektronų koncentracija deiniojoje darinio pusėje 10¹⁶cm^–3. Greta pagrindinių krūvininkų abiejose darinio pusėse yra alutinių krūvininkų. Jų koncentracijas galime rasti i iraikos . Kai temperatūra 300 K, savųjų krūvininkų koncentracija silicyje yra 1,5 10¹⁰ cm^–3. Tada elektronų koncentracija kairiojoje darinio pusėje 2,25 10⁴ cm^–3, skylių koncentracija deiniojoje pusėje 2,25 10⁴ cm^–3.

Dėl didelių krūvininkų koncentracijų gradientų pn sandūroje vyksta jų difuzija. Skylės i p srities difunduoja į n sritį, elektronai i n srities – į p sritį. Dėl difuzijos krūvininkų koncentracijos pn sandūroje kinta ne taip staigiai, kaip legiruojančiųjų priemaių koncentracijos, o palaipsniui (5 pav., b).

Pereinamajame sluoksnyje tarp p ir n sričių krūvininkų koncentracijos yra daug kartų ma˛esnės nei u˛ jo ribų. Kai 0, tai .Vadinasi, pn sandūroje susidaro nuskurdintasis sluoksnis su ma˛a krūvininkų koncentracija ir didele savitąja var˛a.

Difunduodamos i p srities į n sritį, skylės p srityje palieka nesukompensuotus neigiamus akceptorių jonus. Difunduodami i n srities į p sritį, elektronai palieka nesukompensuotus teigiamus donorų jonus. Taip pn sandūroje susidaro erdviniai krūviai (5 pav., c), kurių tankio pasiskirstymas atvaizduotas 5 paveiksle, d.

Tarp erdvinių krūvių atsiranda elektrinis laukas. 5 paveiksle, e, atvaizduotas elektrinio lauko stiprio pasiskirstymo grafikas.

Dėl krūvininkų koncentracijų gradientų ir elektrinio lauko per pn sandūrą teka difuziniai ir dreifiniai krūvininkų srautai.

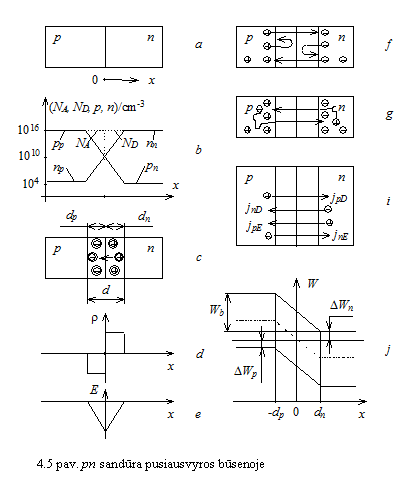
Difuzinius srautus ir difuzines skylinę ir elektroninę sroves per pn sandūrą sudaro pagrindiniai krūvininkai, difunduojantys koncentracijų ma˛ėjimo kryptimis. Įveikę pn sandūrą jie tampa alutiniais krūvininkais (5 pav., f). Pagrindinių krūvininkų difuziją stabdo pn sandūros vidinis elektrinis laukas. Nepakankamai energijos turinčius pagrindinius krūvininkus elektrinis laukas grą˛ina atgal: skyles – į p sritį, elektronus – į n sritį (5 pav., f).

Dreifinius srautus ir dreifines elektroninę bei skylinę sroves sukuria alutiniai krūvininkai. p ir n srityse alutiniai krūvininkai juda chaotikai. Priartėjusius prie pn sandūros alutinius krūvininkus pagauna vidinis elektrinis laukas, greitina ir pernea per sandūrą. Per pn sandūrą perneti alutiniai krūvininkai tampa pagrindiniais (5 pav., g).

I aptarimo aiku, kad elektros srovę per pn sandūrą sudaro keturios dedamosios: skylinė difuzinė, elektroninė difuzinė, skylinė dreifinė ir elektroninė dreifinė srovės. ių srovių tankiai – , , ir (5 pav., i).

Kai neveikia iorinis elektrinis laukas, pn sandūroje nusistovi dinaminė pusiausvyra, kuriai esant difuzinė ir dreifinė srovės kompensuoja viena kitą, ir srovė per pn sandūrą neteka. Vadinasi,

, (15)

(16)

; (17)

čia – per pn sandūrą tekančios difuzinės srovės tankis, – dreifinės srovės tankis.

Pusiausvyros sąlygomis Fermio lygmuo yra vienodas visame darinyje. U˛ pn sandūros ribų p srityje Fermio lygmuo yra ˛emiau draud˛iamosios juostos vidurio, n srityje – vir draud˛iamosios juostos vidurio. Remiantis iais teiginiais galima sudaryti pn sandūros energijos lygmenų diagramą (5 pav., j). Pagal energijos lygmenų diagramą pn sandūroje energijos lygmenų ir padėtys kinta ir krūvininkams susidaro potencialo barjerai. ie barjerai atsiranda todėl, kad pn sandūroje veikia elektrinis laukas ir tarp n ir p sričių veikia kontaktinis potencialų skirtumas . Barjero auktis ireikiamas formule:

; (18)

čia

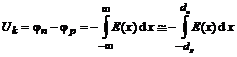. (19)

ioje formulėje ir yra nuskurdintųjų sluoksnių storiai n ir p srityse (5 pav., j).

Įraę į (19) formulę elektrinio lauko stiprio iraikas (3) ir (4), galime gauti:

. (20)

Vidutinių temperatūrų srityje, kai ir ,

. (21)

Pagal ią formulę kontaktinis potencialų skirtumas tarp n ir p sričių tuo didesnis ir potencialo barjeras pn sandūroje tuo auktesnis, kuo didesnės priemaių koncentracijos ir .

Pagal 5 paveikslą, j, galioja ryys

Didėjant priemaių koncentracijoms, p srityje Fermio lygmuo artėja prie valentinės juostos viraus (0), n srityje – prie laidumo juostos viraus (0). Tada barjero auktis artėja prie draud˛iamosios juostos pločio . Taigi maksimalus potencialų skirtumas tarp n ir p sričių ireikiamas formule:

Kai med˛iaga – silicis, tai 1,1 V.

pn sandūroje susidariusį elektrinį lauką, kontaktinį potencialų skirtumą ir potencialo barjerą gali įveikti tik turintys pakankamai kinetinės energijos elektronai. Jei elektrono kinetinė energija ma˛esnė u˛ barjero auktį, jis gali tik įsiskverbti į pn sandūrą. Ieikvojęs energiją darbui, nukreiptam prie elektrinio lauko jėgą, elektronas sustoja. Po to elektrinis laukas tą elektroną grą˛ina į n sritį. Analogiki procesai vyksta, kai i p srities į n sritį juda skylės.

Priartėjusius prie pn sandūros alutinius krūvininkus elektrinis laukas veikia prieingai: ne stabdo, o greitina. Judančių per pn sandūrą alutinių krūvininkų kinetinė energija didėja. Susidurdami su kristaline gardele, alutiniai krūvininkai praranda kinetinę energiją. Jei tokie susidūrimai vyksta pn sandūroje, krūvininkai periodikai praranda kinetinę energiją ir tarsi slysta barjeru.

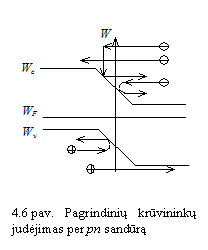
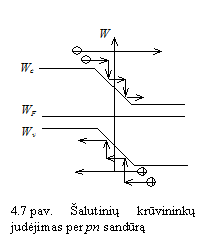
Pagrindinių krūvininkų judėjimą per pn sandūrą iliustruoja 6 paveikslas. Elektronai ir skylės, kaip pagrindiniai krūvininkai, juda koncentracijų ma˛ėjimo kryptimis. Potencialo barjeras stabdo difuziją. Vienam i elektronų nepakanka energijos pn sandūrai įveikti. Kitas elektronas pn sandūroje susiduria su gardele ir praranda kinetinę energiją. Elektrinis laukas jį grą˛ina atgal į n sritį. Potencialo barjerą įveikia tik elektronai ir skylės, turintieji pakankamai didelę pradinę kinetinę energiją ir nesusiduriantieji sandūroje su gardele.

7 paveikslas iliustruoja alutinių krūvininkų judėjimą per pn sandūrą. alutiniai krūvininkai gali laisvai judėti per sandūrą. Jeigu krūvininkas sandūroje nesusiduria su gardele, jo kinetinė energija, judant per sandūrą, didėja. Susidurdami su gardele, krūvininkai slysta pn sandūros potencialo barjeru į kitą pn darinio sritį.

2 u˛duotis

Silicio pn sandūra – staigi. . Apskaičiuokime kontaktinį potencialų skirtumą ir potencialo barjero auktį pn sandūroje, kai T=300 K.

Sprendimas

Pagal (21)

Pagal (18)

eV.

Čia minuso ˛enklas rodo, kad n srityje energijos lygmenys ˛emesni nei p srityje.

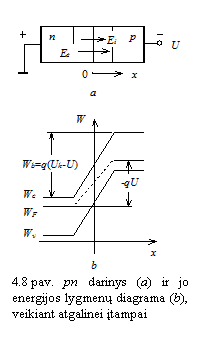
3. pn sandūros voltamperinė charakteristika

Prijungus prie pn sandūros iorinę įtampą, sutrinka krūvininkų difuzijos ir dreifo pusiausvyra ir per sandūrą ima tekėti srovė. ios srovės priklausomybė nuo įtampos yra netiesinė ir vadinama pn sandūros voltamperine charakteristika.

Sakykime, kad iorinė įtampa prijungta minusu prie p srities ir pliusu prie n srities. Kadangi p ir n sričių var˛os yra daug ma˛esnės u˛ nuskurdintojo sluoksnio var˛ą, praktikai visa iorinė įtampa krinta pn sandūroje. Iorinė įtampa sandūroje sukuria iorinį elektrinį lauką (external – iorinis), kurio kryptis nagrinėjamu atveju sutampa su vidinio elektrinio lauko (internal – vidinis) kryptimi (8 pav., a). Padidėjus potencialų skirtumui tarp n ir p sričių, padidėja potencialo barjero auktis pn sandūroje. Pagal 8 paveikslą, a, b, jis ireikiamas formule:

; (22)

čia – kontaktinis potencialų skirtumas tarp n ir p sričių, – iorinė įtampa tarp p ir n sričių.

Priartėję prie pn sandūros alutiniai krūvininkai patenka į elektrinį lauką, kuris juos pernea per sandūrą į kitą pn darinio sritį. Tokių krūvininkų skaičius priklauso nuo alutinių krūvininkų koncentracijos. Nuo elektrinio lauko stiprio jis nepriklauso. Todėl dreifinė pn sandūros srovė nepriklauso nuo potencialo barjero aukčio.

Didėjant barjero aukčiui, jį gali įveikti vis ma˛iau pagrindinių krūvininkų. Nagrinėdami elektronų pasiskirstymą laidumo juostoje galėtume įsitikinti, kad, didėjant barjero aukčiui, skaičius n srities elektronų, kurie gali barjerą įveikti, ma˛ėja eksponentiniu dėsniu. i ivada tinka ir p srities skylėms. Todėl, didėjant 8 paveiksle, a, nurodytai įtampai ir barjero aukčiui, difuzinė srovė per pn sandūrą spar

čiai silpnėja. Paveiksle nurodyto polikumo įtampa () yra atgalinė įtampa (kartais ji dar vadinama atbuline ar atvirktine įtampa).

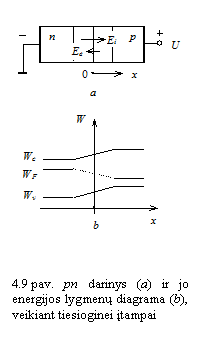
Pakeitus įtampos polikumą – prijungus tiesioginę įtampą (9 pav., a), pasikeičia jos sukurto elektrinio lauko kryptis. pn sandūroje veikiančio elektrinio lauko stipris suma˛ėja. Suma˛ėja ir potencialo barjero auktis (9 pav., b). Suma˛ėjus barjero aukčiui, dreifinė pn sandūros srovė nepakinta. Difuzinė srovė, didėjant tiesioginei įtampai ir ma˛ėjant barjero aukčiui, stiprėja eksponentiniu dėsniu. Įrodoma, kad difuzinės srovės tankis ireikiamas formule:

; (23)

čia – proporcingumo koeficientas, kurio prasmę atskleisime vėliau.

Kadangi pn sandūros srovę sudaro difuzinė ir dreifinė dedamosios, galime rayti:

(24)

Pusiausvyros būsenoje, kai 0, pagal (17) ir (24) formules

. (25)

I čia . Tada, pagal (24), veikiant bet kokiai įtampai, srovės per pn sandūrą tankis ireikiamas formule:

. (26)

Padauginę srovės tankį i pn sandūros ploto , gauname per pn sandūrą tekančios srovės iraiką. Jos stipris

; (27)

čia .

(27) formulė yra idealios pn sandūros voltamperinės charakteristikos iraika.

300 K temperatūroje 26 mV. Todėl, kai 0,1 V, galioja nelygybė 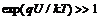. Tada

. (28)

Vadinasi, didėjant tiesioginei įtampai, pn sandūros tiesioginės srovės stipris didėja eksponentiniu dėsniu.

Jeigu veikia atgalinė įtampa ir 0,1 V, tai ir . Vadinasi, kai 0,1 V, didėjant atgalinei įtampai, idealios pn sandūros atgalinė srovė nekinta. Taip yra todėl, kad tada per pn sandūrą teka tik dreifinė srovė, kurios tankis ir stipris nepriklauso nuo veikiančios įtampos ir potencialo barjero aukčio. Srovė vadinama pn sandūros soties srove.

10 paveiksle, a, atvaizduotas idealios pn sandūros voltamperinės charakteristikos grafikas. Veikiant nedidelei tiesioginei įtampai, per pn sandūrą gali tekėti stipri tiesioginė srovė. Atgalinė srovė esti silpna net veikiant didelei atgalinei įtampai. Todėl voltamperinės charakteristikos tiesioginei ir atgalinei akoms parinkti skirtingi masteliai. Tiesioginė įtampa ir tiesioginė srovė pa˛ymėtos ir (forward – tiesioginė), atgalinės įtampa ir srovė – ir (reverse – atgalinė).

10 paveiksle, b, atvaizduota idealios pn sandūros voltamperinės charakteristikos pradinė dalis.

Pagal (27) formulę pn sandūros voltamperinė charakteristika priklauso nuo temperatūros ir soties srovės . Soties srovę lemia alutiniai krūvininkai. alutinių krūvininkų koncentracija lygi ; čia – priemaių koncentracija. Savųjų krūvininkų koncentracija labai priklauso nuo puslaidininkio draud˛iamosios juostos pločio ir temperatūros: Atsi˛velgdami į iuos sąryius, galime rayti:

. (29)

Taigi pn sandūros soties srovė ir voltamperinė charakteristika priklauso nuo sandūros ploto, p ir n sričių legiravimo laipsnio, o ypač – nuo puslaidininkio draud˛iamosios juostos pločio ir temperatūros.

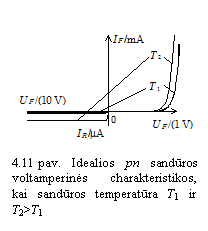
Voltamperinės charakteristikos priklausomybę nuo temperatūros iliustruoja 11 paveikslas. Kylant temperatūrai, stiprėja pn sandūros atgalinė srovė ir ma˛ėja tiesioginė įtampa, atitinkanti tam tikro stiprumo tiesioginę srovę. Nesunku įsitikinti, kad, pakitus temperatūrai 10 ⁰C, silicio pn sandūros soties srovė tampa dvigubai stipresnė. Kadangi tiesioginė įtampa, kylant temperatūrai, ma˛ėja, sakoma, kad tiesioginės įtampos temperatūrinis koeficientas yra neigiamas.

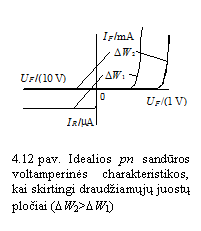
Jei puslaidininkio draud˛iamoji juosta platesnė, alutinių krūvininkų koncentracijos p ir n srityse yra ma˛esnės. Todėl per pn sandūrą teka silpnesnė atgalinė srovė. Be to, kai platesnė draud˛iamoji juosta, susidaro auktesnis potencialo barjeras pn sandūroje. Auktesnį barjerą pajėgia įveikti ma˛iau pagrindinių krūvininkų. Todėl tiesioginė pn sandūros srovė taip pat yra silpnesnė (12 pav.). Dėl to, kad silicio ir germanio draud˛iamųjų juostų pločiai skirtingi, vienodomis sąlygomis per silicio pn sandūrą teka silpnesnė srovė nei per germanio sandūrą.

Voltamperinės charakteristikos priklausomybę nuo priemaių koncentracijos lemia tai, kad, esant didesnei priemaių koncentracijai, yra ma˛esnė alutinių krūvininkų koncentracija ir auktesnis potencialo barjeras. Dėl ių prie˛asčių, kai didesnė priemaių koncentracija, dreifinė ir difuzinė pn sandūros srovės yra silpnesnės.

3 u˛duotis

Kiek kartų germanio diodo soties srovė stipresnė u˛ tokio pat silicio diodo soties srovę 300 K temperatūroje?

Sprendimas

Pagal (29)

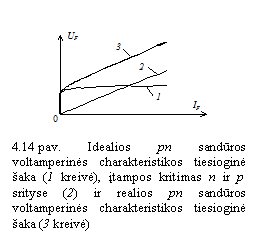
Puslaidininkio kristalo lusto su jame suformuota pn sandūra (realios pn sandūros) voltamperinė charakteristika skiriasi nuo idealios pn sandūros voltamperinės charakteristikos. Prie˛astis galime isiaikinti nagrinėdami realios pn sandūros ekvivalentinę grandinę. Grandinės schemoje (11 pav.) diodas modeliuoja idealią pn sandūrą, var˛a – pn darinio p ir n sričių var˛ą, – nuotėkio var˛ą.

Realios pn sandūros voltamperinės charakteristikos tiesioginei akai did˛iausią įtaką daro var˛a . Kai per pn sandūrą teka tiesioginė srovė, įtampa krinta pn sandūroje ir var˛oje . Todėl

; (30)

čia – realios pn sandūros (puslaidininkio diodo) tiesioginė įtampa, tekant tiesioginei srovei .

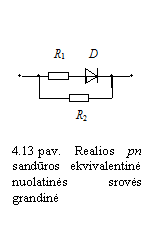
Įtampos kritimo var˛oje įtaką sandūros voltamperinės charakteristikos tiesioginei akai iliustruoja 13 paveikslas.

Dėl įtampos kritimo charakteristikos statumas yra ma˛esnis nei idealios pn sandūros voltamperinės charakteristikos tiesioginės akos statumas. Dėl įtampos kritimo var˛oje per sandūrą teka silpnesnė srovė. Tiesioginė srovė pradeda tekėti, kai tiesioginė įtampa virija tam tikrą slenkstį, kuris priklauso nuo potencialo barjero aukčio, taigi ir nuo puslaidininkio med˛iagos. Germanio diodų slenkstinė įtampa yra apie 0,3 V, silicio diodų – apie 0,7 V.

Dar svarbu pastebėti, kad po to, kai sandūra tampa laidi, didėjant tiesioginei įtampai, dėl įtampos kritimo p ir n srityse tiesioginė srovė kinta ne eksponentiniu dėsniu, o beveik tiesikai. Todėl, nagrinėjant stiprių signalų apdorojimo klausimus, puslaidininkinių diodų voltamperinės charakteristikas galima aproksimuoti lau˛tinėmis linijomis.

pn sandūros atgalinė var˛a esti didelė. Todėl ma˛a var˛a (13 pav.) praktikai neturi įtakos voltamperinės charakteristikos atgalinei akai. Veikiant atgalinei įtampai, didesnės įtakos turi pn sandūrą untuojanti var˛a ir dėl to atsirandanti nuotėkio srovė. Atsi˛velgdami į nuotėkio srovę, gauname:

Didėjant atgalinei įtampai, nuotėkio srovė stiprėja, todėl stiprėja ir atgalinė srovė (15 pav.).

Taigi realios pn sandūros atgalinė srovė būna stipresnė u˛ soties srovę. Tai lemia ne tik nuotėkio srovė. Svarbi realios pn sandūros atgalinės srovės dedamoji yra generavimo srovė. Ją sukuria elektronai ir skylės, generuojami nuskurdintajame pn darinio sluoksnyje dėl iluminių gardelės virpesių. Krūvininkų poras, atsirandančias yrant kovalentiniams ryiams, elektrinis laukas iskiria ir nukreipia į skirtingas sritis. Didėjant atgalinei įtampai, sandūra plečiasi, didėja jos tūris, todėl generavimo srovė stiprėja.

Kai pn sandūros atgalinė įtampa virija leid˛iamąją, atgalinė srovė pradeda staiga stiprėti – prasideda pn sandūros pramuimas ir stiprėja pramuimo srovė.

Taigi realios pn sandūros atgalinę srovę sudaro kelios dedamosios: dreifinė, generavimo, nuotėkio ir pramuimo srovės.

4 u˛duotis

Tekant per puslaidininkinį diodą 5 mA srovei, pn sandūroje krinta 0,7 V įtampa. Diodo p ir n sričių var˛a – 20 W. Raskime diodo tiesioginę įtampą.

Sprendimas

Pagal (30)

5 u˛duotis

Silicio pn sandūroje krinta 0,7 V tiesioginė įtampa. Kiek kartų tekanti per pn sandūrą srovė stipresnė u˛ soties srovę, kai T=300 K?

Sprendimas

Pagal (28)

Taigi pn sandūros tiesioginė srovė daug kartų stipresnė u˛ atgalinę srovę. pn sandūra viena kryptimi gerai praleid˛ia srovę, kita – praktikai nepraleid˛ia. Tai – ventilinė pn sandūros savybė.

pn sandūra veikiant atgalinei įtampai

Nagrinėdami pn darinį pusiausvyros būsenoje įsitikinome, kad pn sandūroje susidaro nuskurdintasis erdvinio krūvio sluoksnis, sudarytas i puslaidininkio atomų ir nesukompensuotų donorinių ir akceptorinių priemaių jonų.

Veikiant atgalinei įtampai, n srities elektronai pasislenka link teigiamojo poliaus, p srities skylės – link neigiamojo poliaus (16 pav.). pn sandūros storis padidėja.

1. pn sandūros storis

pn sandūros storį galima apskaičiuoti sprend˛iant Puasono (Poisson) lygtį. Stačiakampių koordinačių sistemoje Puasono lygtis ireikiama itaip:

; (31)

čia – potencialas, – laisvojo elektros krūvio tankis, , – elektrinė konstanta, – santykinė dielektrinė skvarba.

Kai erdvinis krūvis ir potencialas kinta tik vienos koordinatės kryptimi, Puasono lygtis tampa paprastesnė:

. (32)

Kai pn sandūra staigi, donorų koncentracija n srityje yra , akceptorių koncentracija p srityje – (17 pav.). Vidutinių temperatūrų srityje priemaios jonizuotos. Tada p srityje (kai ) erdvinio krūvio tankis

(33)

n srityje, kai ,

. (34)

Įraę (33) į (32), gauname:

. (35)

Spręsdami ią lygtį, gauname:

; (36)

čia – konstanta.

Tada elektrinio lauko stipris p srities nuskurdintajame sluoksnyje () ireikiamas formule:

. (37)

Kai , elektrinio lauko stipris turi būti lygus nuliui. Tada

(38)

. (39)

Integruodami (39) lygtį, gauname:

. (40)

Kai , potencialas tampa lygus p srities potencialui . Tada ir

. (41)

Analogikai nagrinėdami n srities nuskurdintąjį erdvinio krūvio sluoksnį (), kuriame elektrinio krūvio tankis ireikiamas (34) formule, galime gauti:

(42)

. (43)

Kai 0, skaičiuodami elektrinio lauko stiprį pagal (38) ir (42) formules turime gauti tą patį rezultatą. Todėl

. (44)

Tada

. (45)

Pagal (45) lygtį, kai pn sandūra simetrinė, erdvinio krūvio sluoksniai p ir n srityse yra vienodo storio (). Jeigu , tai erdvinio krūvio sluoksnis storesnis toje srityje, kur priemaių koncentracija ma˛esnė. ią mintį iliustruoja 17 paveikslas, b. Jame pa˛ymėti plotai lygūs sandaugoms ir . Taigi erdvinio krūvio sluoksnio storis atvirkčiai proporcingas priemaių koncentracijai.

Dar pastebėkime, kad pjūvyje 0 p ir n sričių potencialai turi būti vienodi. Tada sulyginę (41) ir (43), gauname:

. (46)

Atsi˛velgę, kad , gauname:

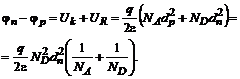(47)

Tada

, (48)

(49)

. (50)

Taigi pn sandūros nuskurdintojo sluoksnio storis priklauso nuo kontaktinio potencialų skirtumo , atgalinės įtampos ir priemaių koncentracijų ir . Kuo didesnės priemaių koncentracijos, tuo pn sandūra plonesnė. Didėjant atgalinei įtampai, pn sandūros storis didėja – pn sandūra plečiasi.

6 u˛duotis

Apskaičiuokime staigiosios silicio pn sandūros storį, kai

Sprendimas

Pagal (50)

Atlikdami 2 u˛duotį gavome, kad 0,85 V. Silicio .

Tada

2. pn sandūros barjerinė talpa

Didėjant atgalinei įtampai ir plečiantis pn sandūrai, joje didėja nesukompensuotų donorų ir akceptorių jonų sukurti krūviai ir , ireikiami formulėmis:

(51)

. (52)

Atsi˛velgus į (45), nesunku įsitikinti, kad absoliutinės krūvių ir vertės yra vienodos:

Taigi krūviai ir priklauso nuo ir , vadinasi, ir nuo atgalinės įtampos. Krūvio kitimas, kintant įtampai, yra talpos po˛ymis. ˇinodami krūvio priklausomybę nuo atgalinės įtampos , pn sandūros talpą galime rasti pagal formulę:

. (53)

Talpa susieta su potencialo barjero pn sandūroje aukčiu ir vadinama pn sandūros barjerine talpa.

Taigi barjerinę talpą galime apskaičiuoti taikydami (53), (51) ir (50) formules. Kita vertus, pn sandūros barjerinės talpos iraiką galime ivesti įsivaizduodami pn sandūrą kaip plokčiąjį kondensatorių – laikydami, kad p ir n sritys yra laidūs kondensatoriaus elektrodai, o nuskurdintasis sluoksnis yra dielektrikas (17 pav., c). Tada

. (54)

Jeigu sandūra simetrinė (), tai

. (55)

Taigi pn sandūros barjerinė talpa tiesiog proporcinga pn sandūros plotui ir priklauso nuo priemaių koncentracijų ir įtampos tarp n ir p sričių. Kuo priemaių koncentracija didesnė, tuo pn sandūra plonesnė, o jos barjerinė talpa didesnė. Didėjant atgalinei įtampai, pn sandūra plečiasi, jos barjerinė talpa ma˛ėja (). Priklausomybė vadinama pn sandūros voltfaradine charakteristika.

(55) formulei galime suteikti pavidalą:

; (56)

čia – proporcingumo koeficientas.

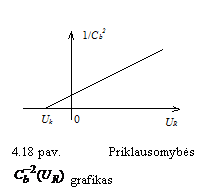
Vadinasi, jeigu pn sandūra staigi, dydis tiesikai priklauso nuo iorinės įtampos.Tada, jeigu pagal matavimų rezultatus sudarytas funkcijos grafikas (18 pav.) yra tiesė, tai galima laikyti, kad pn sandūra yra staigioji. Pagal tiesės polinkio kampą galima spręsti apie pn sandūros sričių legiravimo laipsnį. Tiesės susikirtimo su abscisių aimi takas atitinka kontaktinį potencialų skirtumą (18 pav.).

Jeigu pn sandūra yra simetrinė ir tolydinė, o erdvinio krūvio tankis joje kinta tiesiniu dėsniu (), įrodoma, kad

(57)

(58)

čia – proporcingumo koeficientas, turintis priemaių koncentracijos gradiento prasmę.

Vadinasi, jeigu pn sandūra yra tolydinė, tai tiesikai nuo atgalinės įtampos priklauso dydis .

Vėliau įsitikinsime, kad barjerinė talpa yra svarbus pn sandūros parametras. Siekiant padidinti puslaidininkinių įtaisų veikimo spartą, stengiamasi barjerinę talpą ma˛inti. Kita vertus, pn sandūros talpos priklausomybe nuo įtampos pagrįstas elektriniu būdu valdomų kondensatorių – varikapų – veikimas.

7 u˛duotis

Silicio bandinyje tarp sričių, kuriose priemaių koncentracijos ir sudaryta staigioji pn sandūra, kurios plotas – 0,1 mm. Kaip ir kiek kartų pakis sandūros barjerinė talpa atgalinei įtampai pakilus nuo 1 iki 5 V?

Sprendimas

Pagal (54), didėjant atgalinei įtampai, barjerinė talpa ma˛ėja.

Atlikdami 2 u˛duotį gavome, kad 0,85 V. Tada

5. pn sandūra tekant tiesioginei srovei

Pradėjus veikti tiesioginei įtampai, pn sandūroje suma˛ėja potencialo barjero auktis ir sustiprėja difuzinė srovė. Krūvininkų judėjimą per pn sandūrą bei p ir n sritis, tekant tiesioginei srovei, iliustruoja 19 paveikslas, a, b.

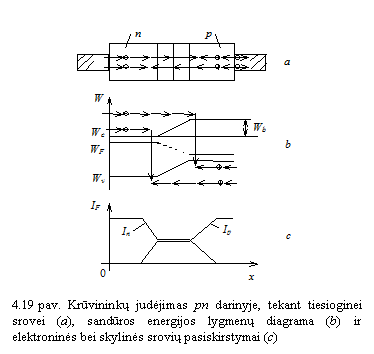
Turintis pakankamai energijos n srities elektronas dreifuodamas p sritimi pasiekia pn sandūrą, difunduoja per ją į p sritį, kurioje tampa alutiniu krūvininku, sutinka p sritimi dreifuojančią skylę ir rekombinuoja. Turinti pakankamai energijos p srities skylė, įveikusi pn sandūrą, tampa n srities alutiniu krūvininku, sutinka elektroną ir rekombinuoja. Pakankamai toli nuo pn sandūros n srityje teka tiesioginė elektroninė srovė , p srityje – tokio pat stiprio skylinė srovė (19 pav., c). Sandūros aplinkoje aies kryptimi elektroninės srovės stipris ma˛ėja, skylinės srovės stipris didėja, tiesioginės srovės stipris nekinta, .

Tekant tiesioginei srovei, vietoj rekombinavusių n srityje ir difundavusių i n srities į p sritį elektronų į n sritį įteka elektronų i metalinio ivado. p srityje vietoj difundavusių ir rekombinavusių skylių naujos skylės atsiranda prie metalinio ivado, iėjus per jį i p srities elektronams. Beje, čia verta prisiminti, kad skylių judėjimas tam tikra kryptimi yra ne kas kitas kaip elektronų judėjimas prieinga kryptimi.

Taigi, pradėjus veikti tiesioginei įtampai, pagrindiniai krūvininkai įveikia pn sandūrą ir kitoje sandūros pusėje padidėja alutinių krūvininkų koncentracijos. is reikinys vadinamas alutinių krūvininkų injekcija.

Sakykime, kad į p sritį buvo injektuota elektronų. Injektuoti elektronai sukuria neigiamą erdvinį krūvį, kuris traukia pagrindinius krūvininkus – skyles. Per trumpą laiką skylės neutralizuoja elektronų erdvinį krūvį ir prie pn sandūros padidėja alutinių ir pagrindinių krūvininkų koncentracijos. Po to vyksta du reikiniai: alutinių krūvininkų difuzija nuo pn sandūros ir jų rekombinacija. Dėl rekombinacijos elektronų tankis ma˛ėja, todėl p srityje koordinatės kryptimi silpnėja elektroninė srovė (19 pav., c). Panaūs reikiniai vyksta kitoje pn sandūros pusėje dėl skylių injekcijos.

Po kokybinio reikinių, kurie vyksta pn sandūros aplinkoje tekant tiesioginei srovei, aptarimo pradėkime kiekybinę analizę. alutinių krūvininkų pasiskirstymą pn sandūros aplinkoje galime rasti spręsdami nenutrūkstamumo lygtį.

5.1. Nenutrūkstamumo lygtis

Nagrinėjant pn sandūras ir puslaidininkinius įtaisus, be Puasono lygties da˛nai taikoma tolydumo lygtis.

Siekdami ivesti tolydumo lygtį, nagrinėkime puslaidininkio bandinį, kurio skerspjūvio plotas lygus vienetui. Sakykime, kad iilgai bandinio veikia elektrinis laukas , o elektronų koncentracija jame kinta aies kryptimi (). Imkime ploną (storio ) bandinio sluoksnį (20 pav.). io sluoksnio tūris yra . Elektronų koncentracija ploname sluoksnyje praktikai pastovi ir laiko momentu yra . Prabėgus laikui , elektronų koncentracija tampa . Tada elektronų skaičiaus pokytį nagrinėjamame sluoksnyje per laiką galime ireikti formule:

. (59)

Elektronų skaičius sluoksnyje gali pakisti dėl jų generacijos, rekombinacijos, difuzijos ir dreifo.

Jei vykstant krūvininkų generacijai bandinio tūrio vienete per laiko vienetą atsiranda elektronų (čia – generavimo sparta), tai nagrinėjamame sluoksnyje, kurio tūris , per laiką elektronų skaičiaus pokytis dėl generacijos lygus . Dėl rekombinacijos elektronų skaičiaus pokytis sluoksnyje yra ; čia – rekombinacijos sparta. Tada elektronų skaičiaus pokytis dėl generacijos ir rekombinacijos ireikiamas formule

. (60)

Dėl krūvininkų koncentracijos gradiento ir elektrinio lauko bandinyje susikuria elektronų srautas. Jei įtekantis į sluoksnį srautas yra , o itekantis srautas yra , tai elektronų skaičius sluoksnyje kinta bėgant laikui. Kadangi bandinio skerspjūvio plotas lygus vienetui, tai elektronų skaičiaus pokytį sluoksnyje per elementarų laiką galime ireikti formule

. (61)

Pagal (59)–(61) formules elektronų skaičiaus pokytį sluoksnyje per laiką galime ireikti lygtimi:

. (62)

Tada

. (63)

Elektronų srautas vienareikmikai susijęs su bandinyje tekančios srovės tankiu:

. (64)

Elektroninę srovę sudaro dreifinė ir difuzinė dedamosios. Pagal (3.54)

. (65)

Pasinaudoję pastarosiomis trimis lygtimis, gauname:

. (66)

Analogiką lygtį galime gauti nagrinėdami skyles:

. (67)

(66) ir (67) lygtys yra tolydumo lygtys. Jomis matematikai ireikiamas krūvio tvermės dėsnis.

5.2. Injektuotų elektronų pasiskirstymas

Taikykime (66) lygtį injektuotiems į p sritį elektronams, siekime rasti injektuotų elektronų pasiskirstymą pagal koordinatę . Kad būtų paprasčiau spręsti u˛davinį, laikykime, kad injektuotų elektronų koncentracija nedidelė, todėl , . Krūvininkų generacijos nepaisykime ir laikykime, kad . Tekant pastovaus stiprumo srovei, elektronų koncentracija nekinta. Tada . Atsi˛velgę į ias prielaidas, (66) lygtį galime supaprastinti. Ji įgyja tokį pavidalą:

. (68)

Pagal (2.67) perteklinių krūvininkų koncentracija, nutrūkus srovei, ma˛ėtų eksponentiniu dėsniu:

. (69)

Tada rekombinacijos sparta

. (70)

Įraę (70) į (68) ir atsi˛velgę, kad , gauname:

(71)

ios lygties sprendinį galime ireikti taip:

; (72)

čia ir – integravimo konstantos, – difuzijos nuotolis,

. (73)

Veikiant tiesioginei įtampai, pn sandūros storis yra ma˛as. Tai leid˛ia supaprastinti pn sandūros modelį – galima laikyti, kad sandūra be galo plona (21 pav.). Tada, atsi˛velgę, kad vyksta injektuotų į p sritį elektronų rekombinacija ir toli nuo sandūros perteklinių elektronų koncentracija lygi 0, gauname, kad (72) lygtyje 0. Kai 0, pagal (72)

. (74)

Tada p srityje

. (75)

Taigi injektuotų į p sritį elektronų koncentracija koordinatės kryptimi ma˛ėja eksponentiniu dėsniu ir priklauso nuo – koncentracijos p srityje prie pn sandūros.

5.3. Perteklinių krūvininkų koncentracijos

Pagal pn sandūros energijos lygmenų diagramą (19 pav., b) p srityje laidumo juostos dugno nuotolis nuo Fermio lygmens yra . Tada, taikydami (2.36) formulę, elektronų koncentraciją p srityje galime ireikti formule:

(76)

Kai veikia tiesioginė įtampa , potencialo barjero auktis ireikiamas formule

. (77)

Tada, įraę (77) į (76), gauname

(78)

Kai 0 ir pn sandūra yra pusiausvyros būsenoje, tai . Atsi˛velgdami į tai gauname, kad

. (79)

Taigi, didėjant tiesioginei įtampai, elektronų koncentracija prie pn sandūros p srityje didėja eksponentiniu dėsniu. Perteklinių elektronų koncentracija p srityje prie pn sandūros ireikiama formule:

(80)

Įraę (80) į (75), gauname:

(81)

Panaiai galime rasti perteklinių skylių koncentracijos pasiskirstymą n srityje. Jis ireikiamas formule:

; (82)

čia – skylių difuzijos nuotolis,

. (83)

I (81), (82) ir (26) formulių palyginimo matyti, kad perteklinių krūvininkų koncentracijos proporcingos per pn sandūrą tekančios srovės tankiui ir eksponentiniu dėsniu ma˛ėja tolstant nuo pn sandūros.

ˇinodami, kaip kinta krūvininkų koncentracijos, galime apskaičiuoti difuzines sroves. Taikydami (3.49) ir (3.52) formules, gauname tokias difuzinių srovių tankių iraikas:

(84)

(85)

Prie sandūros, kai 0,

(86)

(87)

Susumavę iuos srovių tankius, padauginę sumą i pn sandūros ploto ir atmetę minuso ˛enklą, ˛ymintį, kad pagal 19 paveikslą difuzinės srovės teka kryptimi, gauname tokią srovės, tekančios per pn sandūrą, iraiką:

; (88)

čia

(89)

(88) formulė sutampa su anksčiau ivesta pn sandūros voltamperinės charakteristikos iraika. (89) formulė yra sandūros soties srovės iraika.

5. Difuzinė talpa

ˇinant perteklinių alutinių krūvininkų pasiskirstymus (81) ir (82), galima rasti ių krūvininkų sukurtus erdvinius krūvius.

Perteklinių elektronų erdvinis krūvis p srityje ireikiamas formule

. (90)

Įraę į ią formulę perteklinių elektronų koncentracijos iraiką (81), gauname:

(91)

Panaiai galime įrodyti, kad perteklinių skylių krūvis n srityje ireikiamas formule:

. (92)

Krūviai ir parodyti 22 paveiksle. Injektuoti į p sritį elektronai pritraukia skyles, kurių krūvis . Injektuotos į n sritį skylės pritraukia elektronus, kurių krūvis . Bendras prie pn sandūros susikaupęs teigiamas erdvinis krūvis ireikiamas formule:

(93)

I (93) formulės matyti, kad krūvis priklauso nuo įtampos . Tai talpos po˛ymis.

Dydis

(94)

vadinamas pn sandūros difuzine talpa.

Pagal (94) ir (93)

(95)

Pagal (88)

. (96)

Remdamiesi iraikomis (95), (96), (89) ir atsi˛velgę į (73) ir (83), galime įrodyti, kad

(97)

Pagal ią formulę difuzinė pn sandūros talpa proporcinga tekančiai per pn sandūrą difuzinei srovei ir krūvininkų gyvavimo trukmei.

Difuzinė talpa ma˛ina puslaidininkinių įtaisų veikimo spartą. Norint ią talpą suma˛inti, reikia ma˛inti krūvininkų gyvavimo trukmę .

Bendra pn sandūros talpa lygi barjerinės ir difuzinės talpų sumai:

(98)

Kai veikia bent 0,1 V atgalinė įtampa ir difuzinė srovė neteka, tai 0, ir bendra pn sandūros talpa lygi barjerinei talpai . Kai veikia tiesioginė įtampa ir teka tiesioginė srovė, tai , ir bendra pn sandūros talpa apytikriai lygi difuzinei talpai.

8 u˛duotis

300 K temperatūroje per silicio pn sandūrą, veikiant 0,8 V tiesioginei įtampai, teka 10 mA srovė. Krūvininkų gyvavimo trukmė – 1 ms. Apskaičiuokime pn sandūros difuzinę talpą.

Sprendimas

Silicio pn sandūros atgalinė srovė (taigi ir soties srovė) būna silpna. Todėl pagal (97)

6. pn sandūrų pramuimai

Kylant atgalinei įtampai pn sandūros atgalinė srovė pradeda staiga stiprėti (23 pav.) dėl sandūros pramuimo. pn sandūros pamuimas gali būti elektrinis arba iluminis.

Vykstant elektriniam pramuimui, sandūra nesuardoma. Jeigu jis nepereina į iluminį pramuimą, nustojus veikti atgalinei įtampai, visikai atsistato ventilinės pn sandūros savybės. Elektrinis pramuimas būna tunelinis arba griūtinis.

Tunelinis pramuimas įmanomas tuomet, kai priemaių koncentracijos p ir n srityse yra didelės ir pn sandūra yra plona (kai sandūros storis apie 0,01 mm). Plonoje sandūroje, veikiant atgalinei įtampai, susikuria stiprus elektrinis laukas. Stiprus laukas traukia elektronus i kovalentinių ryių ir gali sukelti Zinerio (Zener) efektą – elektrostatinę puslaidininkio atomų jonizaciją. Prasidėjus jonizacijai, padidėja laidumo elektronų ir skylių koncentracijos, suma˛ėja pn sandūros atgalinė var˛a ir sustiprėja atgalinė pn sandūros srovė.

Krūvininkų atsiradimą ir judėjimą, vykstant tuneliniam pramuimui, iliustruoja 24 paveikslas, kuriame atvaizduota pn sandūra ir jos energijos lygmenų diagrama. Veikiant atgalinei įtampai, n srities laidumo juostos apačia atsiduria ˛emiau u˛ p srities valentinės juostos virų. Tada prie elektronų u˛imtus p srities valentinės juostos lygmenis atsiduria laisvi n srities laidumo juostos lygmenys. Juos skiria potencialo barjeras, kurio auktis lygus draud˛iamosios juostos pločiui, o storis – a (24 pav., b). Didėjant atgalinei įtampai, energijos juostos pn sandūroje labiau ilinksta, barjero storis a ma˛ėja, ir elektronai i p srities valentinės juostos tuneliniu būdu pradeda skverbtis į n srities laidumo juostą, palikdami p srityje skyles. Kadangi atgalinė pn sandūros srovė stiprėja dėl tunelinio efekto, aptariamasis pramuimas ir vadinamas tuneliniu pramuimu. Tunelinis pramuimas prasideda, kai elektrinio lauko stipris pn sandūroje virija ma˛daug 10⁷ V/cm. Kadangi tunelinis elektronų skverbimasis įmanomas tik per plonas sandūras, tunelinio pramuimo įtampa būna nedidelė – iki 5–7 V.

4.25 pav. pn sandūra (a) ir jos energijos lygmenų diagrama (b), vykstant griūtiniam pramuimui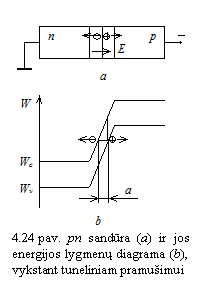

Griūtinis pn sandūros pramuimas gali vykti silpnai legiruotose plačiose pn sandūrose ir prasideda, veikiant silpnesniam elektriniam laukui, krūvininkų koncentracijai didėjant dėl smūginės puslaidininkio atomų jonizacijos. Griūtinio pramuimo prad˛ią iliustruoja 25 paveikslas, kuriame parodyta, kad patekęs į pn sandūrą ir veikiamas elektrinio lauko elektronas greitėja, jo kinetinė energija didėja. Įgijęs pakankamai energijos, susidurdamas su gardele elektronas suardo kovalentinį ryį, ir atsiranda nauja krūvininkų pora. Tada elektrinis laukas greitina jau tris krūvininkus, kurie gali jonizuoti naujus puslaidininkio atomus. Taip pn sandūroje prasideda kovalentinių ryių griūtis, didėja krūvininkų koncentracija ir staiga stiprėja atgalinė pn sandūros srovė.

Griūtinis procesas gali vykti, jeigu pn sandūros storis didesnis u˛ krūvininko laisvąjį kelią. Todėl griūtinis pramuimas galimas tik storose pn sandūrose, susidarančiose tarp silpnai priemaiomis legiruotų p ir n sričių. Todėl griūtinio pramuimo įtampa būna didesnė u˛ 5–7 V.

Prasidėjus elektriniam pramuimui, atgalinės srovės stiprėjimą atitinkanti pramuimo įtampa ma˛ai kinta (23 pav.). Todėl elektrinio pramuimo reikiniai panaudojami nestabilioms nuolatinėms įtampoms stabilizuoti. Tuomet da˛niausiai būna svarbu, kad pramuimo įtampa būtų stabili ir kintant temperatūrai.

Tunelinio pramuimo įtampa, kylant temperatūrai, ma˛ėja. Taip yra todėl, kad, kylant temperatūrai, intensyvėja puslaidininkio gardelės iluminiai virpesiai ir didėja tikimybė, kad kovalentinis ryys suirs. Kai i tikimybė didesnė, kovalentiniai ryiai pradeda irti veikiant silpnesniam elektriniam laukui. Remiantis energijos lygmenų diagrama (24 pav.) į reikinį galima paaikinti tuo, kad, kylant temperatūrai, iek tiek susiaurėja puslaidininkio draud˛iamoji juosta ir todėl ma˛ėja potencialo barjero, per kurį skverbiasi elektronai, auktis ir storis.

Griūtinis pramuimas, kaip įsitikinome, vyksta silpnai legiruotose pn sandūrose. Kai priemaių koncentracija ma˛a, krūvininkų vidutinį laisvąjį kelią lemia jų susidūrimai su fononais. Kylant temperatūrai, fononų koncentracija didėja, o krūvininkų laisvasis kelias trumpėja. Tada pakankamą kinetinę energiją krūvininkas gali įgyti tik, kai jį greitina stipresnis elektrinis laukas, sukuriamas auktesnės įtampos. Todėl, kylant temperatūrai, griūtinio pramuimo įtampa didėja.

Elektrinio pramuimo įtampos temperatūrinį stabilumą apibūdina temperatūrinis koeficientas

;

čia – pramuimo įtampos pokytis, atitinkantis temperatūros pokytį .

Jeigu pramuimas tunelinis, tai temperatūrinis pramuimo įtampos koeficientas yra neigiamas, jeigu pramuimas – griūtinis, tai – teigiamas. Kai pramuimo įtampa yra apie 5–7 V, tai tuo pat metu vyksta abu pramuimai ir tada 0.

Tekant per pn sandūrą srovei, isiskiria D˛aulio (Joule) iluma. Jeigu srovė stipri ir iluma nespėja isisklaidyti, pn sandūra kaista. Kylant temperatūrai, intensyviau ỹra kovalentiniai ryiai, didėja savųjų krūvininkų koncentracija, ma˛ėja pn sandūros atgalinė var˛a ir, veikiant atgalinei įtampai, stiprėja per sandūra tekanti atgalinė srovė. Stiprėjant srovei, pn sandūra dar labiau kaista ir joje suyra dar daugiau kovalentinių ryių. Taip prasideda iluminis pn sandūros pramuimas.

Taigi iluminis pramuimas prasideda perkaitus pn sandūrai. Tunelinis ar griūtinis pramuimas, jeigu srovė per sandūrą neribojama, gali pereiti į iluminį pramuimą. Tai iliustruoja brūknine linija 23 paveiksle atvaizduota voltamperinės charakteristikos dalis.

Vykstant iluminiam pramuimui, suyra labai daug kovalentinių ryių, todėl sutrinka taisyklinga puslaidininkio kristalo struktūra. Po iluminio pramuimo taisyklinga kristalo struktūra nebeatsistato, taigi nebeatsistato ir įprastos sandūros savybės.

Dėl iluminio pramuimo pavojaus puslaidininkinių įtaisų darbo temperatūrų diapazonas yra ribotas. Silicio puslaidininkinių įtaisų did˛iausia darbo temperatūra būna iki 125–200 ⁰C.

7. Ivados

Nevienalyčiame puslaidininkyje dėl krūvininkų koncentracijos gradiento vyksta krūvininkų difuzija koncentracijos ma˛ėjimo kryptimi. Difunduodami koncentracijos ma˛ėjimo kryptimi, krūvininkai palieka nesukompensuotus priemaių jonus. Todėl nevienalyčiame puslaidininkyje susikuria vidinis elektrinis laukas, sukeliantis krūvininkų dreifą. Kai iorinis elektrinis laukas neveikia, pusiausvyros sąlygomis srovė neteka – difuziniai ir dreifiniai krūvininkų srautai sukompensuoja vienas kitą. Pusiausvyros sąlygomis Fermio lygmuo visame nevienalyčio puslaidininkio bandinyje yra vienodas. Energijos lygmenys ir nevienalyčiame puslaidininkyje kyla vidinio elektrinio lauko kryptimi.

pn darinyje tarp p ir n sričių susidaro pn sandūra – nuskurdintasis sluoksnis, pasi˛ymintis didele savitąja var˛a. Difunduodamos koncentracijos ma˛ėjimo kryptimi i p srities į n sritį, skylės p srityje palieka nesukompensuotus neigiamus akceptorių jonus. Difunduodami i n srities, elektronai ioje srityje palieka teigiamus donorų jonus. Taip pn sandūroje susikuria dvigubas erdvinis krūvis. Tarp donorų ir akceptorių jonų susikuria vidinis elektrinis laukas. Jis stabdo pagrindinių krūvininkų difuziją ir sukelia alutinių krūvininkų dreifą per pn sandūrą. Dėl vidinio elektrinio lauko pn sandūroje susidaro kontaktinis potencialų skirtumas. Kai neveikia iorinė įtampa, Fermio lygmuo visame pn darinyje yra vienodas. Dėl vidinio elektrinio lauko ir kontaktinio potencialų skirtumo pn sandūroje susidaro potencialo barjeras. Dėl krūvininkų koncentracijos gradiento ir vidinio elektrinio lauko per pn sandūrą teka skylių difuzinis, elektronų difuzinis, skylių dreifinis ir elektronų dreifinis srautai. Kai neveikia iorinis elektrinis laukas, pn sandūroje nusistovi dinaminė pusiausvyra, difuziniai ir dreifiniai srautai kompensuoja vienas kitą, ir srovė per sandūrą neteka.

Prijungus prie pn sandūros iorinę įtampą, krūvininkų difuzijos ir dreifo pusiausvyra sutrinka, ir per pn sandūrą ima tekėti srovė. Iorinė įtampa, kurios teigiamas polius prijungtas prie p srities, o neigiamas polius – prie n srities, yra laikoma tiesiogine; prieingo polikumo įtampa yra atgalinė. Atgalinės įtampos sukurto elektrinio lauko kryptis sutampa su vidinio pn sandūros elektrinio lauko kryptimi. Didėjant atgalinei įtampai, didėja potencialinio barjero auktis, pn sandūrą įveikia vis ma˛iau pagrindinių krūvininkų, ir silpnėja per pn sandūrą tekanti difuzinė srovė. Dreifinė srovė nuo iorinės įtampos nepriklauso. Veikiant pakankamai didelei atgalinei įtampai, per idealią pn sandūrą teka tik silpna dreifinė soties srovė. Tiesioginė įtampa suma˛ina pn sandūros potencialinio barjero auktį. Didėjant idealios pn sandūros tiesioginei įtampai, eksponentiniu dėsniu auga difuzinės srovės tankis. Tiesioginė pn sandūros srovė gali būti daug kartų stipresnė u˛ atgalinę srovę. Taigi pn sandūra viena kryptimi praleid˛ia srovę, kita – nepraleid˛ia.

Soties srovė ir pn sandūros voltamperinė charakteristika labai priklauso nuo puslaidininkio draud˛iamosios juostos pločio, temperatūros ir priemaių koncentracijų p ir n srityse. Kuo platesnė puslaidininkio draud˛iamoji juosta, tuo silpnesnė soties srovė ir didesnis įtampos kritimas sandūroje, tekant tiesioginei srovei. Kylant temperatūrai, pn sandūros soties srovė sparčiai stiprėja. Kai per pn sandūrą teka pastovaus stiprumo tiesioginė srovė, sandūros įtampa, kylant temperatūrai, ma˛ėja. Kuo didesnės priemaių koncentracijos p ir n srityse, tuo ma˛esnės alutinių krūvininkų koncentracijos ir auktesnis potencialo barjeras pn sandūroje. Todėl, kuo didesnė priemaių koncentracija, tuo silpnesnės būna dreifinė ir difuzinė srovės.

Realios pn sandūros voltamperinės charakteristikos tiesioginei akai turi įtakos įtampos kritimas pn darinio p ir n srityse. Tiesioginė srovė pradeda tekėti, kai tiesioginė įtampa virija slenkstinę įtampą. Atsivėrus sandūrai, tiesioginė srovė beveik tiesikai priklauso nuo tiesioginės įtampos. Realios pn sandūros atgalinė srovė susideda i dreifinės, iluminio generavimo, nuotėkio ir pramuimo srovių.

pn sandūros storis priklauso nuo iorinės įtampos ir priemaių koncentracijos. Didėjant atgalinei įtampai, pn sandūros storis didėja – sandūra plečiasi. Kuo didesnė priemaių koncentracija, tuo pn sandūra plonesnė. Jeigu pn sandūra nesimetrinė, erdvinio krūvio sluoksnio storis didesnis toje srityje, kur priemaių koncentracija ma˛esnė.

Kai, kintant atgalinei įtampai, kinta pn sandūros storis, kartu kinta ir priemaių jonų sukurti krūviai. Todėl pasireikia barjerinė pn sandūros talpa. Ji apskaičiuojama modeliuojant sandūrą kondensatoriumi – laikant, kad p ir n sritys yra laidūs elektrodai, o nuskurdęs sluoksnis yra dielektrikas. Staigios pn sandūros barjerinė talpa tiesiog proporcinga pn sandūros plotui. Be to, ji priklauso nuo priemaių koncentracijos ir įtampos. Kuo priemaių koncentracija didesnė, tuo pn sandūra plonesnė, o jos barjerinė talpa didesnė. Didėjant atgalinei įtampai, pn sandūra plečiasi, jos barjerinė talpa ma˛ėja.

Pradėjus veikti tiesioginei įtampai, suma˛ėja potencialo barjero auktis pn sandūroje ir sustiprėja pagrindinių krūvininkų difuzija per sandūrą. Įveikę pn sandūrą pagrindiniai krūvininkai tampa alutiniais. Taigi, tekant tiesioginei srovei, į p ir n sritis injektuojami alutiniai krūvininkai. Injektuoti alutiniai krūvininkai sukuria erdvinus krūvius, kurie traukia pagrindinius krūvininkus. Per trumpą laiką, prilygstantį dielektrinės relaksacijos trukmei, pagrindiniai krūvininkai neutralizuoja alutinių krūvininkų krūvį. Po to vyksta du procesai: alutinių krūvininkų difuzija nuo pn sandūros ir jų rekombinacija. Perteklinių alutinių krūvininkų koncentracijų pasiskirstymas p ir n srityse, tekant tiesioginei pn sandūros srovei, randamas sprend˛iant nenutrūkstamumo lygtį.

ˇinant perteklinių alutinių krūvininkų pasiskirstymus pn sandūros aplinkoje, galima ivesti sandūros voltamperinės charakteristikos, soties srovės iraikas, o taip pat rasti nepusiausvirųjų krūvininkų sukurtus pn sandūros aplinkoje krūvius. Kadangi ie krūviai priklauso nuo tiesioginės įtampos, pasireikia pn sandūros difuzinė talpa. Difuzinė talpa proporcinga tekančiai per sandūrą difuzinei srovei ir krūvininkų gyvavimo trukmei.

Bendra pn sandūros talpa lygi barjerinės ir difuzinės talpų sumai. Kai veikia atgalinė įtampa ir difuzinė srovė neteka, difuzinė talpa nepasireikia ir pn sandūros talpą lemia barjerinė talpa. Kai veikia tiesioginė įtampa ir teka tiesioginė srovė, pn sandūros talpą nulemia difuzinė talpa, nes ji daug didesnė u˛ barjerinę talpą.

Didėjant atgalinei įtampai, atgalinė srovė staiga stiprėja dėl pn sandūros pramuimo. Vykstant elektriniam pramuimui, sandūra nesuardoma. Jeigu elektrinis pramuimas nepereina į iluminį, nustojus veikti atgalinei įtampai, visikai atsistato ventilinės pn sandūros savybės. Elektrinis pramuimas gali būti tunelinis arba griūtinis. Perkaitus pn sandūrai, prasideda iluminis pramuimas, kurį lemia kovalentinių ryių irimas, vykstant iluminei krūvininkų generacijai. Kai suyra daug kovalentinių ryių, įvyksta negrį˛tamųjų puslaidininkio kristalo struktūros pasikeitimų, todėl po iluminio pramuimo įprastos sandūros savybės nebeatsistato.

8. Kontroliniai klausimai ir u˛duotys

Kokį puslaidininkį vadina nevienalyčiu?

Kaip nevienalyčiame puslaidininkyje susikuria vidinis elektrinis laukas?

Laikydami, kad skylių koncentracijos pasiskirstymas ˛inomas, iveskite vidinio elektrinio lauko stiprio nevienalyčiame puslaidininkyje iraiką.

Sudarykite ir aptarkite nevienalyčių n ir p puslaidininkių energijos lygmenų diagramas.

Kaip galima apskaičiuoti nevienalyčiame puslaidininkyje susidariusio potencialo barjero auktį?

Kodėl, sudarius pn darinį, elektronai i n srities skverbiasi į p sritį, o skylės i p srities skverbiasi į n sritį?

Pusė silicio monokristalo lusto legiruota donorinėmis priemaiomis, kita pusė – akceptorinėmis priemaiomis. Priemaių koncentracijos: , . Sudarykite priemaių ir krūvininkų pasiskirstymo luste grafikus, kai T=300 K. Ordinačių ayje koncentracijas atidėkite logaritminiu masteliu.

Kokia krūvių, sudarančių pn sandūroje dvigubo erdvinio krūvio sluoksnį, prigimtis?

Sudarius pn darinį, vyksta elektronų difuzija i (p,n) srities, skylių – i (p,n) srities; nesukompensuoti teigiamieji jonai lieka pn sandūros (p,n) srityje, neigiamieji jonai – (p,n) srityje.

Kaip pn sandūroje susikuria vidinis elektrinis laukas? Kokia jo kryptis?

Iveskite kontaktinio potencialų skirtumo tarp pn darinio sričių iraiką.

Silicio bandinyje sudaryta staigioji pn sandūra, , . Apskaičiuokite kontaktinį potencialų skirtumą ir potencialo barjero auktį pn sandūroje.

Pagal pastarosios u˛duoties sąlygą ir skaičiavimo rezultatus sudarykite pn sandūros energijos lygmenų diagramą.

Kai elektronas pereina i n srities į p sritį, jo kinetinė energija (padidėja, suma˛ėja).

Ivardinkite tekančios per pn sandūrą srovės dedamąsias. Nurodykite jų kryptis. Paaikinkite susidarymo prie˛astis.

Nurodykite pn sandūros tiesioginės ir atgalinės įtampų polikumus.

Tiesioginė įtampa (padidina, suma˛ina) pn sandūros potencialo barjero auktį.

Kaip difuzinė ir dreifinė pn sandūros srovės priklauso nuo potencialo barjero aukčio?

Iveskite ir inagrinėkite idealios pn sandūros voltamperinės charakteristikos matematinę iraiką.

Silicio pn sandūros soties srovė – 10 pA. Apskaičiuokite tiesiogines sroves, kurios teka, kai sandūroje veikia 0,5, 0,6 ir 0,7 V tiesioginės įtampos.

Ats.: 2,5; 119; 5,7 mA.

Nuo ko, kaip ir kodėl priklauso pn sandūros soties srovė?

Kiek kartų sustiprėja germanio ir silicio pn sandūrų soties srovės kylant temperatūrai nuo 20 iki 100 ^oC?

Ats.: 607; 2,3

Vieno silicio pn darinio p ir n srityse priemaių koncentracija du kartus didesnė nei kito. Raskite pn sandūrų soties srovių santykį.

Nuo ko, kaip ir kodėl priklauso idealios pn sandūros voltamperinės charakteristikos eiga?

Silicio pn sandūros tiesioginė įtampa – 0,7 V. Kaip ir kiek kartų pakis diodo tiesioginė srovė kylant temperatūrai nuo –55 iki 100 ^oC?

Ats.: >6900.

Dėl p ir n sričių var˛ų (padidėja, suma˛ėja) įtampos kritimas diode, tekant per jį tiesioginei srovei , ir (padidėja, suma˛ėja) voltamperinės charakteristikos tiesioginės akos statumas.

Kokios dedamosios sudaro diodo atgalinę srovę? Kokia jų prigimtis?

Diodo pn sandūros soties srovė – 1 mA. Nuotėkio var˛a – 10 MW. Raskite diodo atgalinės srovės stiprumą, veikiant 10 V atgalinei įtampai.

Kaip susidaro iluminio generavimo srovė?

U˛raykite Puasono lygtį. Ką galima rasti sprend˛iant ią lygtį?

Iveskite elektrinio lauko stiprio, potencialo pasiskirstymo staigioje pn sandūroje ir pn sandūros storio iraikas.

Apskaičiuokite staigios silicio pn sandūros storį, kai , , =0, =300 K.

Kaip pn sandūros storis priklauso nuo iorinės įtampos? Kodėl?

Kaip pn sandūros erdvinių krūvių sluoksnių storiai priklauso nuo priemaių koncentracijų?

Kodėl, skaičiuojant barjerinę talpą, pn sandūrą galima modeliuoti kondensatoriumi?

Iveskite pn sandūros barjerinės talpos iraiką.

Barjerinė pn sandūros talpa (didėja, ma˛ėja) augant atgalinei įtampai.

Silicio diodo pn sandūra – staigi, , , sandūros plotas =0,0625 mm². Raskite diodo barjerinę talpą, kai =1 ir 5 V.

Ats.: 4,3 ir 2,4 pF.

Kuo didesnės priemaių koncentracijos p ir n srityse, tuo (didesnė, ma˛esnė) pn sandūros barjerinė talpa.

Iveskite nenutrūkstamumo lygtį.

Aptarkite krūvininkų judėjimą per pn sandūrą, tekant tiesioginei srovei.

Tekant tiesioginei srovei, elektronai injektuojami į (p , n) sritį, skylės – į (p , n) sritį. Kas vyksta po krūvininkų injekcijos?

Kokia yra pn sandūros difuzinės talpos prigimtis?

Iveskite alutinių krūvininkų koncentracijų pasiskirstymo ir pn sandūros voltamperinės charakteristikos iraikas.

Staigiosios pn sandūros parametrai: , , =0,4 /(V s), =0,2 /(V s), =1 ms, =, S=. Apskaičiuokite diodo soties srovę, kai =300 K.

Ats.: 0,12 nA.

Iveskite perteklinių skylių krūvio ir pn sandūros difuzinės talpos iraikas.

Didėjant tiesioginei pn sandūros įtampai, difuzinė pn sandūros talpa (nekinta, didėja, ma˛ėja).

Silicio pn sandūros soties srovė – 1 mA. Krūvininkų gyvavimo trukmė – 1 ms. Apskaičiuokite sandūros difuzinę talpą, kai veikia 0,1, 0,2 ir 0,3 V tiesioginė įtampa.

Paaikinkite, kaip prasideda ir vyksta griūtinis pn sandūros pramuimas?

Kaip griūtinio pramuimo įtampa kinta kylant temperatūrai? Kodėl?

Kaip vyksta tunelinis pramuimas?

Tunelinis pn sandūros pramuimas gali vykti, kai priemaių koncentracijos p ir n srityse (didelės, ma˛os), pn sandūra (stora, plona), elektrinio lauko stiprumas pn sandūroje (didesnis, ma˛esnis) nei 10 V/cm. Tunelinio pramuimo įtampa (esti iki 7 V, virija 7 V).

Kaip tunelinio pramuimo įtampa priklauso nuo temperatūros? Kodėl?

Kaip vystosi iluminis pn sandūros pramuimas?

Kokiuose puslaidininkiniuose įtaisuose taikomi pn sandūros pramuimo reikiniai?

4 sk_r1.doc 2001.10.18 12:52

Politica de confidentialitate | Termeni si conditii de utilizare

DISTRIBUIE DOCUMENTUL

Vizualizari: 3849
Importanta:

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Distribuie URL
https://www.scrigroup.com/limba/lituaniana/255/NEVIENALYIAI-PUSLAIDININKIAI-p52178.php

Adauga cod HTML in site
<a href="https://www.scrigroup.com/limba/lituaniana/255/NEVIENALYIAI-PUSLAIDININKIAI-p52178.php" target="_blank" title=" - https://www.scrigroup.com/limba/lituaniana/255/NEVIENALYIAI-PUSLAIDININKIAI-p52178.php">NEVIENALYČIAI PUSLAIDININKIAI. pn SANDŪROS</a>

NEVIENALYČIAI PUSLAIDININKIAI. pn SANDŪROS

elektra

DOCUMENTE SIMILARE

NEVIENALYČIAI PUSLAIDININKIAI. pn SANDŪROS

1. Nevienalytis puslaidininkis

2. pn sandūra

3. pn sandūros voltamperinė charakteristika

pn sandūra veikiant atgalinei įtampai

1. pn sandūros storis

2. pn sandūros barjerinė talpa

5. pn sandūra tekant tiesioginei srovei

5.1. Nenutrūkstamumo lygtis

5.2. Injektuotų elektronų pasiskirstymas

5.3. Perteklinių krūvininkų koncentracijos

5. Difuzinė talpa

6. pn sandūrų pramuimai

7. Ivados

8. Kontroliniai klausimai ir u˛duotys

DISTRIBUIE DOCUMENTUL

Comenteaza documentul:

6. pn sandūrų pramuimai

7. Ivados