TEORINIAI ELEKTROSTATINIO LAUKO PAGRINDAI

EO sistemose elektrinį lauk¹ paprastai kuria metaliniai elektrodai, turintys tam tikr¹ elektrinį potencial¹. Daugeliu atvejų elektrodų potencialai yra nekintami arba kinta mažu greičiu, todėl elektrodų kuriam¹ elektrinį lauk¹ galima laikyti elektrostatiniu, t.y. galima nepaisyti lauko sklidimo baigtinio greičio ir sūkurinių srovių elektroduose įtakos. Šioje knygos dalyje pateikami pagrindiniai elektrostatinį lauk¹ apibūdinantys dydžiai ir jų s¹ryšiai bei pagrindinės elektrostatinio laiko lygtys ir jų sprendiniai vienalytėje ir diskretiškai nevienalytėje erdvėse. Atkreipkite dėmesį į kraštines elektrostatinio lauko s¹lygas.

1. Lauko stiprumas, potencialas, slinktis

Jėgos, veikiančios nejudam¹ taškinį krūvį q₁, įnešt¹ jį taške Q į elektrinį lauk¹, kuriam¹ kito taškinio krūvio , kuris yra taške M, santykis su krūviu q₁, kai q₁ 0, vadinamas elektrinio lauko stiprumu :

(1)

čia - atstumas-vektorius, nukreiptas iš taško M į tašk¹ Q.

Kadangi pagal (1.14)

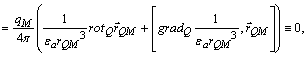
tai elektrostatinis laukas yra potencialinis (nesūkurinis) ir elektrinio lauko stiprumas išreiškiamas skaliarinės funkcijos j gradientu, t.y. . Funkcija j vadinama elektrinio lauko potencialu.

Integruodami išraišk¹ (1), gauname

(2)

Jei vienalytėje aplinkoje yra tūrinės sritys, turinčios tankiu r paskirstyt¹ erdvinį krūvį, paviršinės sritys, turinčios tankiu s paskirstyt¹ paviršinį krūvį ir linijinės sritys, turinčios tankiu t paskirstyt¹ linijinį krūvį, tai visų šių paskirstytųjų laisvųjų krūvių sukurtas elektrinio lauko potencialas bus

(3)

o elektrinio lauko stiprumas (4)

Trečias pagrindinis elektrinio lauko dydis yra elektrinė slinktis

Kai aplinka izotropinė, tai e_a yra skaliarinė koordinačių funkcija ir vektorių ir kryptys sutampa. Anizotropinėje aplinkoje e_a yra tenzorius ir vektorių ir kryptys bendruoju atveju nebesutampa, t.y.

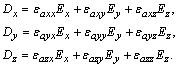(5)

Pasiremdami Maksvelo lygtimi (apibendrint¹ja Gauso teorema),galime užrašyti :

arba ; (6)

čia r - laisvojo krūvio erdvinis tankis. Jei nagrinėjamos erdvės dalyje, apribotoje uždaro paviršiaus S, laisvų krūvių nėra, tai ir .

Puasono ir Laplaso lygtys. Bendruoju atveju ir . Pritaikius (1.13), gaunama:

Jei nagrinėjamoje erdvės dalyje , tai ir, pritaikź (6), gauname:

(7)

Tai Puasono lygtis, kurios vienas iš sprendinių yra (3) lygtis. Jei nagrinėjamoje erdvės dalyje laisvųjų krūvių nėra, tai Puasono lygtis dar vadinama Laplaso lygtimi:

(8)

Puasono ir Laplaso lygtys yra dalinių išvestinių diferencialinės lygtys, turinčios be galo daug sprendinių; tuo tarpu nagrinėjamas laukas turi vienintelį pavidal¹, todėl ir sprendinys turėtų būti vienintelis. Tai galima padaryti į uždavinio sprendinį įtraukus kraštines s¹lygas, t.y. konkrečiuose erdvės taškuose tada yra žinomas potencialas j, elektrinio lauko stiprumas arba slinktis .

Kraštinės elektrostatinio lauko s¹lygos

Tarkim, kad paviršius S skiria du dielektrikus, kurių dielektrinės skvarbos e_a1 ir e_a Be to, paviršius turi paskirstyt¹jį laisv¹jį krūvį, kurio tankis s. Tuomet Gauso teorema teigia, kad

; čia - cilindro paviršiaus plotas (1 pav.). Kadangi

tai, jei cilindro aukštį be galo mažinsime, trečiasis dešinės pusės narys artės prie nulio ir bei , todėl

arba

(9)

Jei paviršiuje S laisvųjų krūvių nėra, tai ir .

Taigi normalinė elektrinės slinkties vektoriaus dedamoji skiriamojoje riboje pakinta šuoliu, lygiu paviršinio krūvio tankiui, arba išlieka nepakitusi, jei laisvųjų krūvių nėra. Tuo tarpu elektrinio lauko stiprumo normalinė dedamoji pakinta bet kuriuo atveju.

Pirmoji Maksvelo lygtis: Skiriamojoje riboje paimkime kontūr¹ L (2 pav.).

Potencialinio elektrinio lauko stiprumo cirkuliacija lygi nuliui, todėl

Mažiname l₄₁ ir l₂₃ ; kadangi ir , tai ir

. (10)

Taigi elektrinio lauko stiprumo tangentinė dedamoji, pereidama dielektrikų skiriam¹j¹ rib¹, nepasikeičia, o elektrinės slinkties tangentinė dedamoji pasikeičia.

Kadangi potencialo pokytis yra ir yra baigtinis dydis, o , tai . Tokiu būdu elektrinio lauko potencialas, pereidamas skiriam¹j¹ rib¹, nepasikeičia, t.y. .

Jei vien¹ dielektrik¹, pavyzdžiui antr¹jį, pakeisime metalu, tai kraštinės s¹lygos bus tokios:

, , , ;

, , , . (11)

Kadangi , tai potencialas visame metalo paviršiuje yra pastovus, t.y. .

3. Elektrostatinis laukas diskretiškai vienalytėje erdvėje

Tai erdvė, turinti įvairius griežtų ribų dielektrikus. Jei aplinka yra veikiama elektrostatinio lauko, tai dielektrikai poliarizuojasi, t.y. dielektriko molekulės ar stambesnis jo darinys tampa dipoliu, kurio momentas ; čia q - dipolio elemento krūvis; - spindulys-vektorius, nukreiptas iš neigiamo krūvio į teigiam¹ (3 pav.). Dipolio kuriamas elektrinio lauko taške Q potencialas yra krūvių –q ir +q kuriamų laukų potencialų superpozicija ir išreiškiamas taip:

(12)

o elektrinio lauko stiprumas

(13)

Atlikź gradiento operacijas, gauname:

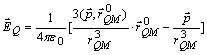(14)

čia - vektoriaus ortas.

Dielektrike yra daug dipolių, ir tūrio vienete esančių dipolių suminis dipolis vadinamas dielektriko poliarizacijos vektoriumi arba dielektriko poliarizuotumu .

Jei dielektrikas poliarizuotas nevienodai, tai sudalijame jį į mažus tūrio elementus , kurių poliarizuotumas Tokio elemento elektrinis momentas , jo kuriamas lauko potencialas taške Q

o viso dielektriko tūrio kuriamas potencialas

(15)

Kadangi

tai

(16)

Pritaikź divergencijos teorem¹ (1.13), gauname

arba

(17)

Palygindami ši¹ išraišk¹ su bendr¹ja potencialo išraiška (3), galime užrašyti, kad  , o ; čia-surištųjų krūvių erdvinis tankis dielektrike, o s - dielektriko surištųjų krūvių paviršinis tankis.Taigi, poliarizavus dielektrik¹, jo paviršiuje atsiranda paviršinių surištiųjų krūvių, kurių tankis , o viduje dielektriko yra tūriniai surištieji krūviai, kurių tankis - (), tačiau bendras poliarizuoto dielektriko krūvis lygus nuliui.

Suminis elektrinio lauko stiprumas dielektrike ; čia - elektrinio lauko stiprumas, sukurtas laisvųjų krūvių; - elektrinio lauko stiprumas, sukurtas surištųjų krūvių. Kadangi ir , tai ir , t.y. visos lauko dedamosios yra potencialinės.

Lauko stiprumo divergencija

Kadangi ir , tai

(19)

Jei dielektrikas izotropinis, tai daugeliu atvejų jo poliarizuotumas yra proporcingas elektrinio lauko stiprumui, t.y. - absoliutinio dielektriškumo koeficientas). Tada

(20)

čia -santykinė dielektriko dielektrinė skvarba .

Jei elektrinio lauko erdvėje yra laidininkų, tai laidininke laisvieji krūviai, veikiami lauko, pasislenka taip, kad laidininko viduje suminis elektrinio lauko stiprumas tampa nulinis, todėl ir, t.y. viduje laidininko erdvinio krūvio nėra ir krūvis, kuriantis laidininke lauk¹, kuris kompensuoja išorinį elektrinį lauk¹, pasiskirsto atitinkamu tankiu s tik laidininko paviršiuje. Paviršinio krūvio tankis ; čia - laidininko išorinės aplinkos dielektrinė skvarba.

Savikontrolės klausimai

Elektrinio lauko potencialas . Raskite elektrinio lauko stiprum¹ .

Kas yra potencialinis laukas? Ar elektrostatinis laukas yra potencialinis? Įrodykite.

Kuo skiriasi Puasono ir Laplaso lygtys? Kada jos turės vienintelį sprendinį?

Kaip pakinta , pereidami iš vieno dielektriko į kit¹?

Kodėl elektriniame lauke laidininkas yra ekvipotencialinis?

Į elektrinį lauk¹ įneškime du nesusiliečiančius laidininkus. Ar jų potencialai bus vienodi?

Kokios yra elektrinio lauko jėgos linijos prie pat laidininko paviršiaus? Kur jos baigiasi arba prasideda?

Kuriuose erdvės taškuose dipolio kuriamas potencialas ir elektrinio lauko stiprumas lygūs nuliui?

Kas yra dielektriko poliarizacijos vektorius (poliarizuotumas) ?

Dielektrikas poliarizuotas vienodai (). Koks bus (17) išraiškos pavidalas?

Stačiakampis gretasienis vienalytis dielektrikas vienodai poliarizuotas išilgai ilgosios kraštinės. Koks bus surištųjų krūvių erdvinis tankis? Kur išdėstytas ir kokio dydžio bus paviršinių surištųjų krūvių tankis?

Metalinis rutuliukas, kurio spindulys R, įkrautas krūviu q. Koks elektrinio lauko stiprumas prie pat rutuliuko paviršiaus? Rutuliuk¹ supa oras.