| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Definicje funkcji trygonometrycznych, ich własności i wykresy.
Funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym.
Niech będzie dany
kąt ostry 
w
trójkącie prostokątnym
przez a, b oznaczamy długości przyprostokątnych trójkąta c- długość przeciwprostokątnej.
Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej kątowi do długości przeciwprostokątnej.
Cosinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do kąta do długości przeciwprostokątnej.
Tangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej kątowi do długości przyprostokątnej przyległej do kąta.
Cotangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do kąta do długości przyprostokątnej przeciwległej kątowi.
Miara łukowa kąta.
Niech będzie dany
kąt środkowy o mierze 
oparty
na łuku 
.
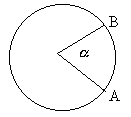
Stosunek długości łuku na którym oparty jest kąt, do długości promienia okręgu jest stały.
Jest on miarą łukową kąta.
Jednostką miary łukowej kąta jest radian (rad).
Jest to kąt środkowy oparty na łuku, którego długość jest równa promieniowi okręgu.
Oznaczmy długość
łuku przez 
promień
przez 
Wówczas:
.
Zatem 
oparty
jest na łuku o długości
Dalej otrzymujemy
Kąt skierowany.
Kątem skierowanym nazywamy uporządkowaną parę półprostych o wspólnym początku.
Pierwszą z tych półprostych nazywamy początkowym ramieniem kąta skierowanego, a drugą –końcowym ramieniem tego kąta.
Jeseli kąt jest skierowany przeciwnie do ruchu wskazówek zegara to ma on miarę dodatnią, jeśli zgodnie to ujemną.
Funkcje trygonometryczne kąta skierowanego.
Dla dowolnego
kąta skierowanego obieramy
układ współrzędnych tak, aby wierzchołek kąta był początkiem układu
współrzędnych, a początkowe ramię kąta pokrywało się z dodatnią półosią OX.
Na końcowym
ramieniu kąta obieramy dowolny punkt P(x, y), oznaczamy 
Wówczas:
Funkcje trygonometryczne zmiennej rzeczywistej.
Funkcją trygonometryczną zmiennej rzeczywistej x nazywamy funkcję trygonometryczną kąta skierowanego, którego miara łukowa jest równa x.
Własności funkcji trygonometrycznych zmiennej rzeczywistej.
Własności
funkcji: 
-dziedzina:
-zbiór wartości
-funkcja
nieparzysta
-funkcja okresowa
o okresie podstawowym 
-wykres:
Własności
funkcji: 
-dziedzina:
-zbiór wartości
-funkcja parzysta
-funkcja okresowa
o okresie podstawowym 
-wykres:
Własności funkcji:
-dziedzina
-zbiór wartości
-funkcja
nieparzysta
-funkcja okresowa
o okresie podstawowym 
-wykres:
Własności funkcji
-dziedzina
-zbiór wartości
-funkcja
nieparzysta
-funkcja okresowa
o okresie podstawowym 
-wykres:
Związki między funkcjami trygonometrycznymi tego samego kąta:
Wzory redukcyjne
Przy pomocy
wzorów redukcyjnych mosna wyrazić wartości funkcji trygonometrycznych dowolnego
kąta przy pomocy wartości funkcji trygonometrycznych kąta, którego miara 
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 2113
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved
