Analiza eficientei algoritmilor

Vom dezvolta in acest capitol aparatul matematic necesar pentru analiza eficientei algoritmilor, urmarind ca aceasta incursiune matematica sa nu fie excesiv de formala. Vom arata apoi, pe baza de exemple, cum poate fi analizat un algoritm. O atentie speciala o vom acorda tehnicilor de analiza a algoritmilor recursivi, prezentati in capitolul 6 al acestui curs.

Notatia asimptotica

Notatia asimptotica are rolul de a estima timpul de calcul necesar unui algoritm pentru a furniza rezultatul, functie de dimensiunea datelor de intrare.

O notatie pentru ordinul de marime al timpului de executie al unui algoritm

Fie multimea numerelor naturale (pozitive sau zero) si multimea numerelor reale. Notam prin si multimea numerelor naturale, respectiv reale, strict pozitive si prin multimea numerelor reale nenegative. Multimea de constante booleene o notam cu . Fie o functie arbitrara. Definim multimea de functii:

astfel incat avem .

Cu alte cuvinte, (se citeste "ordinul lui ") este multimea tuturor functiilor marginite superior de un multiplu real pozitiv al lui , pentru valori suficient de mari ale argumentului n. Vom conveni sa spunem ca este in ordinul lui (sau, echivalent, este in , sau ) chiar si atunci cand este negativ sau nedefinit pentru anumite valori . In mod similar, vom vorbi despre ordinul lui chiar si atunci cand valoarea este negativa sau nedefinita pentru un numar finit de valori ale lui ; in acest caz, vom alege suficient de mare, astfel incat pentru acest lucru sa nu mai apara. De exemplu, vom vorbi despre ordinul lui , chiar daca pentru si functia nu este definita. In loc de , uneori este mai convenabil sa folosim notatia , subintelegand aici ca si sunt functii.

Fie un algoritm dat si fie o functie astfel incat o anumita implementare a algoritmului sa necesite cel mult unitati de timp pentru a rezolva un caz de marime , . Principiul invariantei ne asigura atunci ca orice implementare a algoritmului necesita un timp in ordinul lui . Mai mult, acest algoritm necesita un timp in ordinul lui pentru orice functie pentru care . In particular avem relatia: . Vom cauta, in general, sa gasim cea mai simpla functie , astfel incat .

Exemplu: Fie functia . Pentru n suficient de mare, vom avea relatia . In consecinta, luand , putem spune ca . La fel de bine puteam sa spunem ca , dar pe noi ne intereseaza sa gasim o expresie cat mai simpla. Este adevarata si relatia , dar, asa cum vom vedea mai tarziu, suntem interesati de a margini cit mai strans ordinul de marime al algoritmului, pentru a putea obiectiva cat mai bine durata sa de executie.

Proprietatile de baza ale lui sunt date ca exercitii (1 - 5) si ar fi recomandabil sa le studiati inainte de a trece mai departe.

Notatia asimptotica defineste o relatie de ordine partiala intre functii si deci intre eficienta relativa a diferitilor algoritmi care rezolva o anumita problema. Vom da in continuare o interpretare algebrica a notatiei asimptotice. Pentru oricare doua functii definim urmatoarea relatie binara: daca . Relatia "" este o relatie de ordine partiala (reflexiva, tranzitiva, antisimetrica) in multimea functiilor definite pe si cu valori in (exercitiul 4). Definim si o relatie de echivalenta: daca . Prin aceasta relatie obtinem clase de echivalenta, o clasa de echivalenta cuprinzand toate functiile care difera intre ele printr-o constanta multiplicativa. De exemplu, si avem o clasa de echivalenta a functiilor logaritmice, pe care o notam generic cu . Notand cu clasa de echivalenta a algoritmilor cu timpul marginit superior de o constanta (cum ar fi interschimbarea a doua numere, sau maximul a trei elemente), ierarhia celor mai cunoscute clase de echivalenta este:

Aceasta ierarhie corespunde unei clasificari a algoritmilor dupa un criteriu al performantei. Pentru o problema data, dorim mereu sa obtinem un algoritm corespunzator unei clase cat mai "de jos" (cu timp de executie cat mai mic). Astfel, se considera a fi o mare realizare daca in locul unui algoritm exponential gasim un algoritm polinomial.

Exercitiul 5 ne da o metoda de simplificare a calculelor in care apare notatia asimptotica. De exemplu,

Ultima egalitate este adevarata chiar daca pentru , deoarece notatia asimptotica se aplica doar pentru suficient de mare. De asemenea,

chiar daca pentru polinomul este negativ. Exercitiul 8 trateaza cazul unui polinom oarecare.

Notatia este folosita pentru a limita superior timpul necesar unui algoritm, masurand eficienta (complexitatea computationala) a algoritmului respectiv. Uneori este interesant sa estimam si o limita inferioara a acestui timp. In acest scop, definim multimea

astfel incat avem .

Exista o anumita dualitate intre notatiile si : pentru doua functii oarecare , avem:

daca si numai daca .

O estimare foarte precisa a timpului de executie se obtine atunci cand timpul de executie al unui algoritm este limitat atat inferior cat si superior de cate un multiplu real pozitiv al aceleasi functii. In acest scop, introducem notatia

numita ordinul exact al lui . Pentru a compara ordinele a doua functii, notatia nu este insa mai puternica decat notatia , in sensul ca este echivalent cu .

Exista situatii in care timpul de executie al unui algoritm depinde simultan de mai multi parametri. Aceste situatii sunt tipice pentru anumiti algoritmi care opereaza cu grafuri si la care timpul depinde atat de numarul de varfuri cat si de numarul de muchii. Notatia asimptotica se generalizeaza in mod natural si pentru functii cu mai multe variabile. Astfel, pentru o functie arbitrara definim

astfel incat avem .

Similar se obtin si celelalte generalizari.

Tehnici de analiza algoritmilor

Nu exista o metoda generala pentru analiza eficientei unui algoritm. Este mai curand o chestiune de rationament, intuitie si experienta. Vom arata pe baza de exemple cum se poate efectua o astfel de analiza.

Sortarea prin selectie

Consideram algoritmul de sortare prin selectie din sectiunea 2.2.2.2. Timpul pentru o singura executie a ciclului pentru dupa variabila j poate fi marginit superior de o constanta . In total, pentru un fixat, tinand cont de faptul ca se realizeaza n-i iteratii, acest ciclu necesita un timp de cel mult unitati, unde este o constanta reprezentand timpul necesar pentru initializarea buclei. O singura executie a buclei exterioare are loc in cel mult unitati de timp, unde este o alta constanta. Tinand cont de faptul ca bucla dupa j se realizeaza de n-1 ori, timpul total de executie al algoritmului este cel mult:

unitati de timp, fiind din nou o constanta. Simplificam aceasta expresie si obtinem , de unde deducem ca algoritmul necesita un timp in . O analiza similara asupra limitei inferioare arata ca timpul este de fapt in . Nu este necesar sa consideram cazul cel mai nefavorabil sau cazul mediu deoarece timpul de executie este independent de ordonarea prealabila a elementelor de sortat.

In acest prim exemplu am analizat toate detaliile. De obicei insa, detalii cum ar fi initializarea ciclurilor nu se vor considera explicit. Pentru cele mai multe situatii, este suficient sa alegem o anumita instructiune din algoritm ca barometru si sa numaram de cate ori se executa aceasta instructiune. In cazul nostru, putem alege ca barometru testul

a[i] < a[PozMin]

din bucla interioara, acest test executandu-se de ori.

Sortarea prin insertie

Timpul pentru algoritmul de sortare prin insertie (sectiunea 2.2.2.3) este dependent de ordonarea prealabila a elementelor de sortat. Vom folosi comparatia

b[j]<a[i]

din ciclul cat timp ca barometru.

Sa presupunem ca este fixat si fie elementul care se insereaza in algoritm. Cel mai nefavorabil caz apare atunci cand pentru fiecare intre si , algoritmul facand in aceasta situatie comparatii. Acest lucru se intampla pentru fiecare valoare a lui de la la atunci cand tabloul este initial ordonat descrescator. Numarul total de comparatii pentru cazul cel mai nefavorabil este

Vom estima acum timpul mediu necesar pentru un caz oarecare. Presupunem ca elementele tabloului sunt distincte si ca orice permutare a lor are aceeasi probabilitate de aparitie. Atunci, daca , probabilitatea ca sa fie cel de-al -lea cel mai mare element dintre elementele este . Pentru un fixat, conditia este falsa cu probabilitatea , deci probabilitatea ca sa se execute comparatia "" o singura data inainte de iesirea din bucla while este . Comparatia "" se executa de exact doua ori tot cu probabilitatea , etc. Probabilitatea ca sa se execute comparatia de exact ori este , deoarece aceasta se intampla atat cand cat si cand ! Numarul mediu de comparatii, pentru un fixat, este in consecinta, suma numarului de comparatii pentru fiecare situatie, inmultita cu probabilitatea de aparitie a acelei situatii:

Pentru a sorta elemente, avem nevoie de comparatii, ceea ce este egal cu . Prin am notat al -lea termen al seriei armonice.

Se observa ca algoritmul de sortare prin inserare efectueaza pentru cazul mediu de doua ori mai putine comparatii decat pentru cazul cel mai nefavorabil. Totusi, in ambele situatii, numarul comparatiilor este in .

Cu toate ca algoritmul necesita un timp in atat pentru cazul mediu cat si pentru cel mai nefavorabil caz, pentru cazul cel mai favorabil (cand initial tabloul este ordonat crescator) timpul este in . De fapt, pentru cazul cel mai favorabil, timpul este si in (deci in ).

Turnurile din Hanoi

Matematicianul francez Eduard Lucas a propus in 1883 o problema care a devenit apoi celebra mai ales datorita faptului ca a prezentat-o sub forma unei legende. Se spune ca Brahma (Zeul Creatiei la hindusi) a fixat pe Pamant trei tije de diamant si pe unul din ele a pus in ordine crescatoare 64 de discuri de aur de dimensiuni diferite, astfel incat discul cel mai mare era jos. Brahma a creat si o manastire, iar sarcina calugarilor era sa mute toate discurile pe o alta tija. Singura operatiune permisa era mutarea cate unui singur disc de pe o tija pe alta, astfel incat niciodata sa nu se puna un disc mai mare peste un disc mai mic. Legenda spune ca sfarsitul lumii se va petrece atunci cand calugarii vor savarsi lucrarea. Aceasta se dovedeste a fi o previziune extrem de optimista asupra sfarsitului lumii. Presupunand ca in fiecare secunda se muta un disc si lucrand fara intrerupere, cele 64 de discuri nu pot fi mutate nici in 500 de miliarde de ani de la inceputul actiunii!

Pentru a rezolva problema, observam ca pentru a muta cele mai mici discuri de pe tija pe tija (unde ) este necesar sa transferam cele mai mici discuri de pe tija pe tija apoi transferam discul de pe tija pe tija , iar apoi retransferam cele discuri de pe tija pe tija . Cu alte cuvinte, reducem problema mutarii a discuri la problema mutarii a discuri. Urmatoarea procedura descrie acest algoritm recursiv.

procedura Hanoi(n,i,j)

daca atunci

Hanoi(n-1, i, 6-i-j)

scrie i j

Hanoi(n-1, 6-i-j, i)

return

Pentru rezolvarea problemei initiale, facem apelul Hanoi(.

Consideram instructiunea scrie ca barometru. Timpul necesar algoritmului este exprimat prin urmatoare recurenta:

Vom demonstra in sectiunea 3 ca . Rezulta .

Acest algoritm este optim in sensul ca este imposibil sa mutam discuri de pe o tija pe alta cu mai putin de operatii. Pentru a muta 64 de discuri vor fi in consecinta necesare un numar astronomic de 2⁶⁴ operatii. Implementarea in oricare limbaj de programare care admite exprimarea recursiva se poate face aproape in mod direct.

Analiza algoritmilor recursivi

Am vazut in capitolul 6 si in exemplul precedent cat de puternica si in acelasi timp cat de eleganta este recursivitatea in elaborarea unui algoritm. Cel mai important castig al exprimarii recursive este faptul ca ea este naturala si compacta, fara sa ascunda esenta algoritmului prin detaliile de implementare. Pe de alta parte, apelurile recursive trebuie folosite cu discernamant, deoarece solicita si ele resursele calculatorului (timp si memorie). Analiza unui algoritm recursiv implica aproape intotdeauna rezolvarea unui sistem de recurente. Vom vedea in continuare cum pot fi rezolvate astfel de recurente. Incepem cu tehnica cea mai simpla.

Metoda iteratiei

Cu putina experienta si intuitie putem rezolva de multe ori astfel de recurente prin metoda iteratiei: se executa primii pasi, se intuieste forma generala, iar apoi se demonstreaza prin inductie matematica ca forma este corecta. Sa consideram de exemplu recurenta problemei turnurilor din Hanoi. Pentru un anumit obtinem succesiv

Rezulta . Prin inductie matematica se demonstreaza acum cu usurinta ca aceasta forma generala este corecta.

Inductia constructiva

Inductia matematica este folosita de obicei ca tehnica de demonstrare a unei asertiuni deja anuntate. Vom vedea in aceasta sectiune ca inductia matematica poate fi utilizata cu succes si in descoperirea enuntului asertiunii. Aplicand aceasta tehnica, putem simultan sa demonstram o asertiune doar partial specificata si sa descoperim specificatiile care lipsesc si datorita carora asertiunea este corecta. Vom vedea ca aceasta tehnica a inductiei constructive este utila pentru rezolvarea anumitor recurente care apar in contextul analizei algoritmilor. Incepem cu un exemplu.

Fie functia definita prin recurenta

Sa presupunem pentru moment ca nu stim ca si sa cautam o astfel de formula. Avem

si deci . Aceasta ne sugereaza sa formulam ipoteza inductiei specificate partial conform careia este de forma . Aceasta ipoteza este partiala in sensul ca , si nu sunt inca cunoscute. Tehnica inductiei constructive consta in a demonstra prin inductie matematica aceasta ipoteza incompleta si a determina in acelasi timp valorile constantelor necunoscute , si .

Presupunem ca este adevarata pentru un anumit . Atunci, . Daca dorim sa aratam ca este adevarata, trebuie sa aratam ca . Prin identificarea coeficientilor puterilor lui , obtinem ecuatiile si , cu solutia , putand fi oarecare. Avem acum o ipoteza mai completa, pe care o numim tot . Am aratat ca daca este adevarata pentru un anumit , atunci este adevarata si . Ramane sa aratam ca este adevarata si . Trebuie sa aratam ca .Stim ca , deci este adevarata pentru . In concluzie am demonstrat ca pentru orice .

Recurente liniare omogene

Exista din fericire si tehnici care pot fi folosite aproape automat pentru a rezolva anumite clase de recurente. Vom incepe prin a considera ecuatii recurente liniare omogene, adica de forma

(*)

unde sunt valorile pe care le cautam, iar coeficientii sunt constante.

Conform intuitiei[3], vom cauta solutii de forma

unde este o constanta (deocamdata necunoscuta). Daca inlocuim aceasta solutie in (*), obtinem

Solutiile acestei ecuatii sunt fie solutia triviala , care nu ne intereseaza, fie solutiile ecuatiei

care se numeste ecuatia caracteristica a recurentei liniare si omogene(*).

Presupunand deocamdata ca cele radacini ale acestei ecuatii caracteristice sunt distincte, se verifica usor ca orice combinatie liniara

este o solutie a recurentei (*), unde constantele sunt determinate de conditiile initiale. Se poate demonstra faptul ca (*) are solutii numai de aceasta forma.

Sa exemplificam prin recurenta care defineste sirul lui Fibonacci (sectiunea 6.1)

iar . Putem sa rescriem aceasta recurenta sub forma , care are ecuatia caracteristica

cu radacinile . Solutia generala are forma

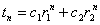
Impunand conditiile initiale, obtinem

de unde determinam

Deci, . Observam ca si obtinem

care este cunoscuta relatie a lui Moivre, descoperita la inceputul secolului XVIII. Nu prezinta nici o dificultate sa aratam acum ca timpul pentru functia Fib (sectiunea 6.1) este in .

Cum procedam insa atunci cand radacinile ecuatiei caracteristice nu sunt distincte? Se poate arata ca daca este o radacina de multiplicitate a ecuatiei caracteristice, atunci sunt solutii pentru (*). Solutia generala pentru o astfel de recurenta este atunci o combinatie liniara a acestor termeni si ai termenilor proveniti de la celelalte radacini ale ecuatiei caracteristice. Din nou, sunt de determinat exact constante din conditiile initiale.

Vom da din nou un exemplu. Fie recurenta

cu . Ecuatia caracteristica are radacinile 1 (de multiplicitate 1) si 2 (de multiplicitate 2). Solutia generala este:

.

Din conditiile initiale, obtinem .

Recurente liniare neomogene

Consideram acum recurente de urmatoarea forma mai generala

(**)

unde este o constanta, iar este un polinom in de grad . Ideea generala este ca prin manipulari convenabile sa reducem un astfel de caz la o forma omogena.

De exemplu, o astfel de recurenta poate fi

In acest caz, si , un polinom de grad . O simpla manipulare ne permite sa reducem acest exemplu la forma (*). Inmultind recurenta cu , obtinem

Inlocuind pe cu in recurenta originala, avem

In final, scadem aceste doua ecuatii si obtinem

Am obtinut o recurenta omogena pe care o putem rezolva ca in sectiunea precedenta. Ecuatia caracteristica este

adica .

Intuitiv, observam ca factorul corespunde partii stangi a recurentei originale, in timp ce factorul a aparut ca rezultat al manipularilor efectuate pentru a scapa de partea dreapta.

Iata al doilea exemplu:

Manipularile necesare sunt putin mai complicate. Trebuie sa:

Inmultim recurenta cu

Inlocuim in recurenta pe cu

Inlocuim in recurenta pe cu si sa inmultim apoi cu

Adunand cele trei ecuatii obtinute prin (i), (ii) si (iii), obtinem

Am ajuns din nou la o ecuatie omogena. Ecuatia caracteristica corespunzatoare este

adica .

Inca o data, observam ca factorul provine din partea stanga a recurentei originale, in timp ce factorul este rezultatul manipularii.

Generalizand acest procedeu, se poate arata ca pentru a rezolva (**) este suficient sa luam urmatoarea ecuatie caracteristica:

Odata ce s-a obtinut aceasta ecuatie, se procedeaza ca in cazul omogen.

Vom rezolva acum recurenta corespunzatoare problemei turnurilor din Hanoi

iar . Rescriem recurenta astfel

care este de forma (**) cu si , un polinom cu grad 0. Ecuatia caracteristica este atunci , cu solutiile si . Solutia generala a recurentei este

Avem nevoie de doua conditii initiale. Stim ca ; pentru a gasi cea de-a doua conditie calculam

Din conditiile initiale, obtinem .

Observatie: daca ne intereseaza doar ordinul lui , nu este necesar sa calculam efectiv constantele in solutia generala. Daca stim ca , rezulta ca . Din faptul ca numarul de mutari a unor discuri nu poate fi negativ sau constant (deoarece avem in mod evident ), deducem ca . Avem atunci si deci . Putem obtine chiar ceva mai mult.

Substituind solutia generala inapoi in recurenta originara, gasim

.

Indiferent de conditia initiala, este deci .

Schimbarea variabilei

Uneori putem rezolva recurente mai complicate printr-o schimbare de variabila. In exemplele care urmeaza, vom nota cu termenul general al recurentei si cu termenul noii recurente obtinute printr-o schimbare de variabila. Presupunem pentru inceput ca este o putere a lui .

Un prim exemplu este recurenta

in care inlocuim pe cu , notam si obtinem

Ecuatia caracteristica a acestei recurente liniare este

si deci . Inlocuim la loc pe cu

Rezulta ca .

Un al doilea exemplu il reprezinta ecuatia

Procedand la fel, ajungem la recurenta

cu ecuatia caracteristica

si solutia generala . Atunci,

,

si obtinem ca ,

In fine, sa consideram si exemplul

fiind o constanta. Obtinem succesiv

cu ecuatia caracteristica

si, deoarece

obtinem

deci, .

In toate aceste exemple am folosit notatia asimptotica conditionata. Pentru a arata ca rezultatele obtinute sunt adevarate pentru orice , este suficient sa adaugam conditia ca sa fie eventual nedescrescatoare. Aceasta, datorita proprietatii 3.1 si a faptului ca functiile si sunt netede.

Putem enunta acum o proprietate care este utila ca reteta pentru analiza algoritmilor cu recursivitati de forma celor din exemplele precedente. Proprietatea, a carei demonstrare o lasam ca exercitiu, este foarte utila la analiza algoritmilor Divide et Impera prezentati in capitolul 6.

Propozitie. Fie o functie eventual nedescrescatoare

unde: si sunt intregi; si sunt numere reale pozitive; este o putere a lui . Atunci avem

Exercitii

1. Care din urmatoarele afirmatii sunt adevarate?

(i)

(ii)

(iii)

(iv)

(v) pentru orice functie ,

avem:

(vi) pentru orice functie ,

avem:

2. Demonstrati ca relatia "" este tranzitiva: daca si , atunci . Deduceti de aici ca daca atunci .

3. Gasiti doua functii astfel incat si .

Indicatie: ,

4. Pentru oricare doua functii definim urmatoarea relatie binara: daca . Demonstrati ca relatia "" este o relatie de ordine partiala in multimea functiilor definite pe si cu valori in .

Indicatie: Trebuie aratat ca relatia este partiala (deci nu totala), reflexiva, tranzitiva si antisimetrica. Tineti cont de exercitiul 4.

5. Pentru oricare doua functii demonstrati ca , unde suma si maximul se iau punctual.

6. Fie un polinom de grad , cu . Aratati ca .

7. . Unde este eroarea?

. Unde este eroarea?

9. Pentru oricare doua functii demonstrati ca , unde suma si maximul se iau punctual.

10. Analizati eficienta urmatorilor algoritmi:

(i)  pentru i = 1,n

pentru j = 1,5

pentru i = 1,n

pentru j = 1,i+1

(iii)  pentru i = 1,n

pentru j = 1,6

pentru k = 1,n

(iv)  pentru i = 1,n

pentru j = 1, i

pentru k = 1,n

11. Construiti un algoritm cu timpul in .

12. Fie urmatorul algoritm

pentru i = 0,n

j i

cat timp j <> 0

j j div 2

Gasiti ordinul exact al timpului de executie.

13. Rezolvati urmatoarea recurenta

,

cu , .

14. Care este ordinul timpului de executie pentru un algoritm recursiv cu recurenta

Indicatie: Se ajunge la ecuatia caracteristica , iar solutia generala este . Rezulta ca .

Substituind solutia generala inapoi in recurenta, obtinem ca, indiferent de conditia initiala, si . Atunci, toate solutiile interesante ale recurentei trebuie sa aiba si ele sunt toate in , deci in .