Metoda Divide et Impera

Metoda Divide et Impera

Metoda Divide et Impera ('desparte si stapaneste') consta in impartirea repetata a unei probleme de dimensiuni mari in mai multe subprobleme de acelasi tip, urmata de rezolvarea acestora si combinarea rezultatelor obtinute pentre a determina rezultatul corespunzator problemei initiale. Pentru fiecare subproblema procedam in acelasi mod, cu exceptia cazului in care dimensiunea ei este suficient de mica pentru a fi rezolvata direct.

Este evident caracterul recursiv al acestei metode.

Schema generala

Descriem schema generala pentru cazul in care aplicam metoda pentru o prelucrare oarecare asupra elementelor unui vector. Functia DivImp, care intoarce rezultatul prelucrarii asupra unei subsecvente a_p,a_u, va fi apelata prin DivImp(1,n).

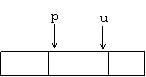function DivImp(p,u)

if u-p<ε

then r ← Prel(p,u)

else m ← Interm (p,u);

r1 ← DivImp(p,m);

r2 ← DivImp(m+1,u);

r ← Combin(r1,r2)

return r

end;

unde:

functia Interm intoarce un indice in intervalul p..u (de obicei m= (p+u)/2û ).

functia Prel este capabila sa intoarca rezultatul subsecventei p..u, daca aceasta este suficient de mica;

functia Combin intoarce rezultatul asamblarii rezultatelor partiale r1 si r2.

Exemple:

Calculul maximului elementelor unui vector;

Parcurgerile in preordine, inordine si postordine ale unui arbore binar;

Sortarea folosind arbori de sortare.

Cautarea binara

Se considera vectorul a=(a₁, ,a_n) ordonat crescator si o valoare x. Se cere sa se determine daca x apare printre componentele vectorului.

Problema enuntata constituie un exemplu pentru cazul in care problema se reduce la o singura subproblema.

Tinand cont de faptul ca a este ordonat crescator, vom compara pe x cu elementul din 'mijlocul' vectorului. Daca avem egalitate, algoritmul se incheie; in caz contrar vom lucra fie pe 'jumatatea' din stanga, fie pe cea din dreapta.

Vom adauga a=-∞, a_n+1=+ ∞. Cautam perechea (b,i) data de:

(true,i) daca a_i=x;

(false,i) daca a_i-1<x<a_i.

Deoarece problema se reduce la o singura subproblema, nu mai este necesar sa folosim recursivitatea.

Algoritmul este urmatorul:

procedure CautBin

p ← u; u ← n

while p≤u

i ← (p+u)/2û

case a_i>x : u ← i-1

a_i=x : write(true,i); stop

a_i<x : p ← i+1

write(false,p)

end

Algoritmul necesita o mica analiza, legata de corectitudinea sa partiala. Mai precis, ne intrebam: cand se ajunge la p>u?

pentru cel putin 3 elemente : nu se poate ajunge la p>u;

pentru 2 elemente, adica pentru u=p+1: se alege i=p. Daca x<a_i, atunci u p-1. Se observa ca se iese din ciclul while si a_i-1<x<a_i=a_p;

pentru un element, adica p=u: se alege i=p=u. Daca x<a_i atunci u p-1, iar daca x>a_i atunci p u+1; in ambele cazuri se paraseste ciclul while si tipareste un rezultat corect.

Problema turnurilor din Hanoi

Se considera 3 tije. Initial pe tija 1 se afla n discuri cu diametrele decrescatoare privind de la baza catre varf, iar pe tijele 2 si 3 nu se afla nici un disc. Se cere sa se mute aceste discuri pe tija 2, ajutandu-ne si de tija 3, respectand conditia ca in permanenta pe orice tija sub orice disc sa se afle baza tijei sau un disc de diametru mai mare.

O mutare este notata prin (i,j) si semnifica deplasarea discului din varful tijei i deasupra discurilor aflate pe tija j. Se presupune ca mutarea este corecta (vezi conditia de mai sus).

Fie H(m;i,j) sirul de mutari prin care cele m discuri din varful tijei i sunt mutate peste cele de pe tija j, folosind si a treia tija, al carei numar este evident 6-i-j. Problema consta in a determina H(n;1,2).

Se observa ca este satisfacuta relatia:

H(m;i,j)= H(m-1;i,j) (i,j) H(m-1;i,j)

respectandu-se conditia din enunt. Deci problema pentru m discuri a fost redusa la doua probleme pentru m-1 discuri, al caror rezultat este asamblat conform (*).

Corespunzator, vom executa apelul Hanoi(n,1,2), unde procedura Hanoi are forma:

procedure Hanoi(n,i,j)

if n=1

then write(i,j)

else k 6-i-j;

Hanoi(n-1,i,k); Hanoi(1,i,j); Hanoi(n-1,k,j)

end

Observatie. Numarul de mutari este 2ⁿ-1.

Sortare prin interclasare

Fie a=(a₁,,a_n) vectorul care trebuie ordonat crescator.

Ideea este urmatoarea: impartim vectorul in doi subvectori, ordonam crescator fiecare subvector si asamblam rezultatele prin interclasare. Se observa ca este aplicata tocmai metoda Divide et Impera.

Incepem cu procedura de interclasare. Fie secventa de indici p..u si fie m un indice intermediar. Presupunand ca (a_p,,a_m) si (a_m+1,,a_u) sunt ordonati crescator, procedura Inter va ordona crescator intreaga secventa (a_p,,a_u).

Mai precis, vom folosi notatiile:

k1 = indicele curent din prima secventa;

k2 = indicele curent din a doua secventa;

k3 = pozitia pe care va fi plasat cel mai mic dintre a_k1 si a_k2 intr-un vector auxiliar b.

procedure Inter(p,m,u)

k1 p; k2 m+1; k3 p;

while k1£m & k2£u

if a_k1<a_k2 then k1 k1+1; b_k3 a_k1

else k2 k2+1; b_k3 a_k2

k3 k3+1

if k1>m

then for i=k2,u

b_k3 a_i; k3 k3+1

else for i=k1,m

b_k3 a_i; k3 k3+1

for i=p,u

a_i b_i

end

Timpul de calcul este de ordinul O(u-p), adica liniar in lungimea secventei analizate.

Programul principal urmeaza intocmai strategia Divide et Impera, deci se face apelul SortInter(1,n), unde procedura recursiva SortInter are forma:

procedure SortInter(p,u)

if p=u

then

else m (p+u)/2û

SortInter(p,m); SortInter(m+1,u);

Inter(p,m,u)

end

Calculam in continuare timpul de executare T(n), unde T(n) se poate scrie:

t₀ (constant), pen tru n=1;

2T(n/2)+an, pentru n>1, unde a este o constanta: problema de dimensiune n s-a descompus in doua subprobleme de dimensiune n/2, iar combinarea rezultatelor s-a facut in timp liniar (prin interclasare).

Presupunem ca n=2^k. Atunci:

T(n) = T(2^k) =2 T(2^k-1) + a 2^k =

=2[2T(2^k-2) + a 2^k-1] + a 2^k = 2²T(2^k-2) + 2 a 2^k =

=2²[T(2^k-3) + a 2^k-2] + 2 a 2^k = 2T(2^k-3) + 3 a 2^k =

. . .

= 2ⁱT(2^k-i) + i a 2^k =

. . .

=2^kT(0) + k a 2^k = nt₀ + a n logn.

Rezulta ca T(n)=0(n log n).

Se observa ca s-a obtinut acelasi timp ca si pentru sortarea cu ansamble.

Mentiune. Se poate demonstra ca acest timp este optim.

Metoda Quicksort 

Prezentam inca o metoda de sortare a unui vector a=(a₁,,a_n). Va fi aplicata tot metoda Divide et Impera. Si de aceasta data fiecare problema va fi descompusa in doua subprobleme mai mici de aceeasi natura, dar nu va mai fi necesara combinarea (asamblarea) rezultatelor rezolvarii subproblemelor.

Fie (a_p,,a_u) secventa curenta care trebuie sortata. Vom pozitiona pe a_p in secventa (a_p,,a_u), adica printr-o permutare a elementelor secventei:

x=a_p va trece pe o pozitie k;

toate elementele aflate la stanga pozitiei k vor fi mai mici decat x;

toate elementele aflate la dreapta pozitiei k vor fi mai mari decat x.

In acest mod a_p va aparea pe pozitia sa finala, ramanand apoi sa ordonam crescator elementele aflate la stanga sa, precum si pe cele aflate la dreapta sa.

Fie poz functia cu parametrii p,u care intoarce indicele k pe care va fi pozitionat a_p in cadrul secventei (a_p,,a_u).

Atunci sortarea se realizeaza prin apelul QuickSort(1,n), unde procedura QuickSort are forma:

procedure QuickSort(p,u)

if p=u

then

else k poz(p,u); QuickSort(p,k-1); QuickSort(k+1,n)

end

Functia poz lucreaza astfel:

function poz(p,u)

i p; j u; ii 0; jj

while i<j

if a_i<a_j

then

else a_i<a_j; (ii,jj) (-ii,-jj)

i i+ii; j j+jj  (*)

poz ← i

end

Sa urmarim cum decurg calculele pentru secventa:

(a₄,,a₁₁)=(6,3,2,5,8,1,9,7)

se compara cu a₁₁,a₁₀, pana cand gasim un element mai mic. Acesta este a₉=1. Se interschimba cu . Acum secventa este si vom lucra in continuare pe subsecventa , schimband directia de comparare conform ;

va fi comparat succesiv cu pana cand gasim un element mai mare. Acesta este a₈=8. Se interschimba cu .

Se obtine astfel , in care la stanga lui apar valori mai mici, iar la dreapta lui apar valori mai mari, deci l-am pozitionat pe pe pozitia , valoare intoarsa de functia poz.

Observatie. Cazul cel mai defavorabil pentru metoda Quicksort este cel in care vectorul este deja ordonat crescator: se compara a₁ cu a₂,,a_n rezultand ca el se afla pe pozitia finala, apoi se compara a₂ cu a₃,,a_n rezultand ca el se afla pe pozitia finala etc.

Trecem la calculul timpul mediu de executare al algoritmului Quicksort. Vom numara cate comparari se efectueaza (componentele vectorului nu sunt neaparat numere, ci elemente dintr-o multime ordonata oarecare). Timpul mediu este dat de formulele:

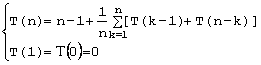
deoarece:

in cazul cel mai defavorabil a₁ se compara cu celelalte n-1 elemente;

a₁ poate fi pozitionat pe oricare dintre pozitiile k=1,2,,n; consideram aceste cazuri echiprobabile;

T(k-1) este timpul (numarul de comparari) necesar ordonarii elementelor aflate la stanga pozitiei k, iar T(n-k) este timpul necesar ordonarii elementelor aflate la dreapta pozitiei k.

nT(n) = n(n-1)+2[T(0) +T(1)+..+T(n-1)]

(n-1)T(n-1) = (n-1)(n-2)+2[T(0)+..+T(n-2)]

Scazand cele doua reltii obtinem:

nT(n)-(n-1)T(n-1) = 2(n-1)+ 2T(n-1), dci:

nT(n) = (n+1)T(n-1)+2(n-1).

Impart cu n(n+1):

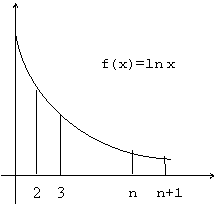
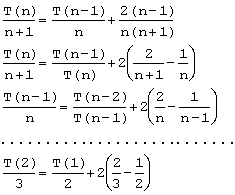
Prin adunarea relatiilor de mai sus obtinem:

Cum suma ultimilor doi termeni este negativa, rezulta:

ln(n+1)

(am folosit o inegalitate bazata pe sumele Rieman pentru functia f(x)=ln x).

Deci T(n)=0(n^.log n).

Incheiem cu mentiunea ca metoda Divide et Impera are o larga aplicativitate in calculul paralel.