Reprezentarea naturala a arborilor

Reprezentarea naturala a arborilor

Tema nr. 1:

Scrieti programul C care permite crearea si vizualizarea sub forma naturala a unui arbore binar ordonat.

Scrieti programul C care permite crearea si vizualizarea sub forma naturala a unui arbore perfect echilibrat.

Obs:

La fiecare din cele doua teme afisati arborele in inordine, postordine si preordine.

Analiza:

Daca dorim sa vizualizam sub forma naturala un arbore in limbajul C avem nevoie sa lucram in modul grafic.

Se stie ca monitorul oricarui terminal (compus din ecran si circuite de generare a imaginii) poate lucra in doua moduri: modul text si modul grafic.

In modul text ecranul este impartit in randuri (rows) si coloane (columns). Numarul de randuri si numarul de coloane este dat de modul de lucru permis de monitor. De obicei sunt 25 de randuri si 80 de coloane. La intersectia unei linii cu o coloana se genereaza un caracter printr-o matrice de puncte luminoase. Pentru fiecare pozitie de afisare, se vor pastra (din motive de reimprospatare a imaginii) codul ASCII (Unicode) al caracterului si atributul caracterului (cel care controleaza aspectul caracterului afisat si depinde de adaptorul folosit). De exemplu, pentru calculatoare personale, codul caracterului este stocat folosind 8 biti, iar atributul folosind alti 8 biti. Atributul pentru afisarea color este format din trei elemente:

culoarea penitei (foreground),

culoare hartiei (background),

elementul de control al clipirii (blink>).

Culoarea este specificata cu ajutorul a trei componente fundamentale:

R - rosu (Red),

G - verde (Green),

B - albastru (Blue).

In modul grafic ecranul este o suprafata de puncte luminoase numite pixeli (elemente de imagine - picture element).

Urmatoarele elemente caracterizeaza un anumit mod grafic:

Rezolutia - numarul de puncte de pe ecran;

Definitia - distanta dintre doua puncte pe ecran;

Numarul de culori.

Toate aceste elemente depind de modul grafic suportat de monitor.

De exemplu:

Ø     modul MDA (Monochrome Display Adapter) asigura o rezolutie de 720350 puncte si este monocrom.

Ø     modul CGA (Color Graphics Adapter) - standard grafic aparut in 1981 cu rezolutiile 160200 puncte in 16 culori, 320200 puncte in 4 culori, 640200 puncte in doua culori.

Ø     modul EGA (Enhanced Graphics Adapter) - produce in mod grafic rezolutiile 640350 pixeli in 16 culori, 320200 pixeli in 16 culori, 640200 in 16 culori, iar in mod text 640350 cu 16 culori si 720350 cu 4 culori.

Ø     modul VGA (Video Graphics Array) - produs in 1987 de catre IBM, produce toate modurile EGA si inca cateva noi, din care cele mai populare sunt doua: unul asigura o rezolutie de 640480 pixeli si 16 culori, iar celalalt asigura o rezolutie de 320200 si 256 de culori.

Ø     modul SVGA (Super Video Graphics Array) - standard grafic aparut in 1989, produce in mod grafic o rezolutie de 800600 pixeli in 256 culori.

Ø     modul XGA (eXtended Graphics Array) - standard grafic produs in 1990 de catre IBM, cu rezolutiile in mod grafic 640480 pixeli in 256 sau 65536 culori, 1024768 pixeli cu 256 culori, iar in mod text 1056400 cu 16 culori.

Ø     modul SXGA (Super eXtended Graphics Array) asigura o rezolutie maxima de 12801024 pixeli cu pana la 16,7 milioane de culori.

Ø     modul UXGA (Ultra eXtended Graphics Array) asigura o rezolutie maxima de 16001200 pixeli cu pana la 16,7 milioane de culori.

Ø     modul WXGA (Wide eXtended Graphics Array) asigura o rezolutie maxima de 1366768 pixeli cu pana la 16,7 milioane de culori.

Ø     modul WSXGA (Wide Super eXtended Graphics Array) asigura o rezolutie maxima de 16801050 pixeli.

Ø     modul WUXGA (Wide Ultra eXtended Graphics Array) asigura o rezolutie maxima de 19201200 pixeli.

Pentru gestiunea ecranului in mod grafic, mediul Borland C++ foloseste interfata grafica BGI (Borlang Graphics Interface), driverul grafic uzual fiind EGAVGA, si pune la dispozitie peste 80 de functii grafice elementare. Aceste functii au prototipul in fisierul graphics.h.

Practic, pentru a realiza o aplicatie grafica in C trebuiesc parcurse urmatoarele etape:

initilizarea (setarea) modului grafic

testarea ca intr-adevar s-a setat modul de lucru grafic;

stabilirea culorii de fundal;

stabilirea culorii de scris;

desenarea efectiva;

inchiderea modului de lucru grafic.

Setarea modului grafic se realizeaza cu ajutorul functiei initgraph.

Sintaxa functiei este:

void initgraph (int *driver_grafic, int *modul_grafic, char *cale_spre_driver);

Aceasta functie initializeaza sistemul grafic incarcand un driver grafic de pe disk (sau validand un driver instalat) si apoi punand sistemul in modul grafic.

De asemenea initgraph reseteaza toate setarile grafice (culoare, paleta, pozitia curenta, etc.) la setarile initiale, si pune graphresult pe 0.

Functia initgraph poate fi folosita impreuna cu functia detectgraph, care are rolul de a detecta adaptorul grafic al sistemului si de a alege modul care furnizeaza cea mai mare rezolutie pentru acel adaptor. Daca nu detecteaza hardware grafic, detectgraph seteaza *driver_grafic pe grNotDetected, si graphresult o sa returneze grNotDetected.

Sintaxa functiei detectgraph este:

void detectgraph (int *driver_grafic, int *modul_grafic);

Ex: Pentru setarea modului grafic putem folosi secventa de instructiuni:

int driver_grafic, mod_grafic;

detectgraph(&driver_grafic, &mod_grafic);

initgraph(&driver_grafic, &mod_grafic, "C:BORLANDCBGI");

Insa functia initgraph nu are neaparata nevoie de functia detectgraph, existand instructiunea de detectare automata a driverului grafic, astfel ca pentru setarea modului grafic mai putem folosi si urmatoarele instructiuni:

int driver_grafic, mod_grafic;

driver_grafic = DETECT;

initgraph(&driver_grafic, &mod_grafic, "C:BORLANDCBGI");

in acest caz modul grafic fiind stabilit implicit de catre program.

Testarea ca s-a initializat modul grafic se efectueaza cu ajutorul functiei graphresult. Sintaxa acestei functii este: int graphresult (void);

graphresult retuneaza codul erorii ultimei operatii grafice ce a raportat o eroare (un intreg intre -15 si 0, 0 fiind daca nu s-a produs nici o eroare) dupa care reseteaza nivelul de eroare la grOk.

Variabila pastrata de graphresult este resetata la 0 dupa apelul lui graphresult. De aceea este indicat sa se pastreze valoarea returnata de graphresult intr-o variabila temporara, pentru a fi testata ulterior.

Fiecare intreg intre -15 si -1 returnat de graphresult ce reprezinta un cod de eroare. Exista o functie numita grapherrormsg care preia valoarea returnata de graphresult si returneaza un pointer la un mesaj de eroare asociat valorii respective. Asadar sintaxa functiei grapherrormsg este:

char *grapherrormsg (int errorcode);

Din cele aratate mai sus, putem construi o functie care initializeaza modul grafic, si testeaza desfasurarea cu succes a initializarii astfel:

void initializare_mod_grafic(void)

} /* initializare_mod_grafic */

Stabilirea culorii de fundal se realizeaza prin intermediul functiei setbkcolor, ce are sintaxa: void setbkcolor (int culoare);

unde culoare poate fi un numar intreg pozitiv, fie o constanta simbolica. Corespondenta este urmatoarea:

astfel, pentru a realiza un fundal albastru putem proceda astfel:

setbkcolor(BLUE);

sau:

setbkcolor(1);

Tot aici merita amintita functia getbkcolor, care, asa cu ii spune si numele, returneaza culoarea curenta a fundalului. Sintaxa ei este:

int getbkcolor (void);

Aceasta functie este folosita in special atunci cand dorim sa stergem ceva de pe ecran. De exemplu daca dorim sa stegem o linie de pe ecran setam culoarea de desenare cu valoarea returnata de getbkcolor si desenam o linie cu aceleasi coordonate ale capetelor ca si linia pe care dorim sa o stergem.

Stabilirea culorii de scris se realizeaza prin intermediul functiei setcolor, ce are sintaxa: void setcolor (int culoare);

unde culoare poate fi exact ca si la functia setbkcolor.

Si aici exista o functie care returneaza culoarea curenta de desenare, ea se numeste getcolor, si are sintaxa: int getcolor (void);

Desenarea efectiva

Pentru a inceput trebuie sa precizam modul in care sunt definite coordonatele pe ecran. Spre deosebire de modul in care sunt definte cordonatele unui punct in plan in matematica, interfata grafica BGI defineste astfel coordonatele pe ecran:

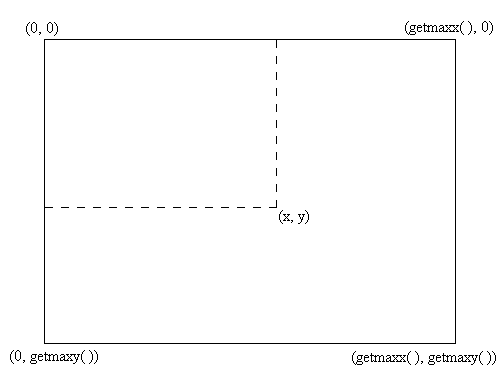
Astfel, coltul din stanga sus are coordonatele , valoarea lui crescand spre dreapta, iar valoarea lui crescand in jos.

Dupa cum se poate observa si din desen, exista 2 functii puse la dispozitie de biblioteca grafica a mediului Borland C++ pentru detectarea coordonatelor maxime admise pentru driverul si modul de lucru curent:

functia getmaxx returneaza coordonata maxima pe orizontala.

Sintaxa ei este: int getmaxx (void);

functia getmaxy returneaza coordonata maxima pe verticala.

Sintaxa ei este: int getmaxy (void);

Pe langa aceste 2 functii mai exista si alte doua functii care returneaza coordonatele pixelului curent:

functia getx returneaza abscisa pixelului curent.

Sintaxa ei este: int getx (void);

functia gety returneaza ordonata pixelului curent.

Sintaxa ei este: int gety (void);

Aceste 4 functii nu modifica pozitia curenta a cursorului. Intr-o fereastra text, deplasarea cursorului pe o anumita pozitie o realizeaza functia gotoxy. Aceasta are sintaxa: void gotoxy (int x, int y);

Daca coordonatele si din apelul functiei sunt valide aceasta are ca efect mutarea cursorului pe pozitia , daca nu sunt valide (pot fi prea mari) atunci functia nu are nici un efect.

In modul grafic acest efect este produs de catre functia moveto, ce are sintaxa: void moveto (int x, int y);

Desenarea unei linii se efectueaza de catre functia line. Aceasta are sintaxa: void line (int x1, int y1, intx2, int y2);

Prin apelul acestei functii se traseaza o linie de la la folosind culoarea curenta, iar pozitia curenta ramane nemodificata.

Mai putem desena o linie si prin apelul functiei lineto, daca dorim sa desenam o linie incepand din pozitia curenta. Aceasta are sintaxa:

void lineto (int x, int y);

Prin apelul acestei functii se traseaza o linie din pozitia curenta la punctul de coordonate , insa se modifica si pozitia curenta, aceasta devenind

Pentru a desena un arbore mai avem nevoie sa desenam discuri. Pentru aceasta putem folosi doua functii:

functia pieslice desenaza un sector de disc cu culoarea si textura curenta. Sintaxa ei este: void pieslice(int x, int y, int stangle, int endangle, int radius);

unde reprezinta coordonatele centrului discului, iar acesta va fi cuprins intre unghiul stangle si unghiul endangle (in grade) si va avea raza egala cu radius.

functia fillellipse deseneaza si umple o elipsa cu culoarea si textura curenta. Sintaxa ei este: void fillellipse(int x, int y, int xradius, int yradius);

unde reprezinta coordonatele centrului elipsei, xradius reprezinta semiaxa mare, iar yradius reprezinta semiaxa mica a elipsei.

Pentru a afisa un text in modul grafic avem la dispozitie doua functii:

functia outtext afisaza un sir de caractere in modul grafic incepand din pozitia curenta. Sintaxa ei este: void outtext(char *textstring);

functia outtextxy afisaza un sir de caractere in modul grafic incepand dintr-o anumita pozitie. Sintaxa ei este: void outtextxy(int x, int y, char *textsring);

unde reprezinta coordonatele pixelului de unde o sa fie afisat textul.

Ambele functii folosesc setarile curente de font, directie si marime, si nu pot fi utilizate in modul text, numai in mod grafic. Insa observam ca ambele functii trimit pe ecran un sir de caractere. Deci, pentru a le putea folosi trebuie sa convertim textul pe care dorim sa-l afisam in sir de caractere. Functia care realizeaza acest lucru este functia sprintf. Sintaxa ei este:

int sprintf (char *buffer, const char *format [, argument, ]);

De obicei desenarea pe ecran se realizeaza instantaneu. Daca insa dorim sa urmarim modul in care se deseneaza atunci trebuie sa "incetinim" procesul de desenare. Pentru aceasta folosim functia delay. Sintaxa acestei functii este:

void delay(unsigned milliseconds);

functia delay suspenda executia programului atatea milisecunde cat este argumentul sau.

Si poate vreodata o sa dorim sa stergem ecranul. Pentru lucrul in mod text avem functia clrscr, iar pentru lucrul in mod grafic avem functia cleardevice. Aceasta are sintaxa: void cleardevice(void);

si are ca efect stergerea intregului ecran (de fapt se umple cu culoarea fundalului) si mutarea pozitiei curente in .

Folosind cele de mai sus, functia care va tipari un nod al unui arbore in mod grafic ar trebui sa primeasca ca si parametru nivelul pe care se afla nodul (care va contribui la cat de jos sa desenam nodul), coordonatele centrului nodului parinte (trebuie sa unim centrul nodului parinte cu centrul nodului fiu printr-o linie), si daca am precizat cat de jos desenam nodul (prin intermediul nivelului nodului) mai trebuie sa precizam si cat de la stanga sau la dreapta il desenam. Regula ar fi urmatoarea: nodul de nivel 0 va avea abscisa getmaxx()/2, cele doua noduri de nivel unu vor avea abscisele getmaxx()/3 si respectiv 2*getmaxx()/3 si asa mai departe.

void Tip(ref anod, int nivel, int x1, int x2, int c1, int c2, char *s)

/*Tip*/

unde si reprezinta coordonatele centrului nodului parinte, iar nodul va fi plasat la mijlocul distantei intre si (pe orizontala).

Aceasta functie va fi aplelata din cadrul functiilor inordine, preordine, postordine, pe care le-am definit semestrul trecut in cazul reprezentarii indentate a arborilor, iar in cazul reprezentarii naturale a arborilor ideea de baza ramane aceeasi:

void inordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*inordine*/

void preordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*preordine*/

void postordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*postordine*/

Inchiderea modului de lucru grafic se realizeaza prin intermediul functiei closegraph. Aceasta are sintaxa: void closegraph(void);

si are ca efect dealocarea memoriei alocate modului grafic. Apoi restabileste ecranul la modul in care era inainte de apelul lui initgraph.

Arbori binari ordonati

Arborii binari ordonati au fost studiati in semestrul trecut, si i-am prezentat in detaliu in laboratorul 13 din caietul de laborator din semestrul trecut

Reamintim ca au fost introdusi in scopul eficientizarii operatiei de cautare in cazul in care cheile nodurilor sunt numere intregi.

Def Un arbore binar se zice ca e ordonat, daca la traversarea nodurilor in inordine secventa cheilor este monoton crescatoare.

Un astfel de arbore se mai numeste arbore binar de cautare.

Obs: Din definitia de mai sus rezulta ca daca este un nod arbitrar al unui astfel de arbore, de cheie , atunci toate nodurile din subarborele sau stang au cheia mai mica decat , iar toate nodurile din subarborele sau drept au cheia mai mare sau egala cu .

Din aceasta observatie rezulta un principiu foarte usor de cautare al unui nod de cheie data intr-un astfel de arbore binar ordonat: se traverseaza arborele incepand cu radacina si se trece la fiul stang sau fiul drept al acestuia, dupa cum cheia nodului de cautat este mai mica, respectiv mai mare decat cheia nodului curent. Acest proces se continua pana cand, fie am gasit un nod care are cheia egala cu cheia nodului cautat, fie pana cand am ajuns la o referinta nula, ceea ce inseamna ca nodul respectiv nu exista in arbore.

Pentru a crea un arbore binar ordonat, vom traversa arborele incepand cu radacina in scopul inserarii noului nod astfel incat dupa inserare arborele sa ramana tot binar si ordonat.

Initial se porneste cu arborele vid, care evident este ordonat.

Traversam arborele incepand cu radacina, si se selecteaza fiul stang sau fiul drept dupa cum cheia nodului de inserat este mai mica, respectiv mai mare sau egala decat cheia nodului curent, pana gasim o referinta nula. Modificam aceasta referinta astfel incat sa indice noul nod introdus.

Crearea unui arbore binar ordonat presupune inserarea unui nou nod in arborele binar ordonat care initial este arborele vid.

Functia care descrie inserarea unui nou nod de cheie intr-un arbore binar ordonat de radacina :

void InArbore(int x, ref *t)

else if(x<(*t)->cheie)

InArbore(x, &((*t)->st));

else InArbore(x, &((*t)->dr));

} /* InArbore */

Astfel, functia de cautare (descrisa mai sus) va intoarce adresa nodului cu cheia daca acest nod exista, sau NULL daca nodul cu cheia nu exista in arbore:

ref Loc(int x, ref t)

/* Loc */

Reamintim si modul in care se suprima un nod dintr-un arbore binar ordonat, deoarece avem nevoie de cunoasterea in detaliu a acestei operatii pentru ca o vom folosi si in cazul arborilor AVL (vezi lab. nr. 3)

Suprimarea: se da un nod de cheie data , si se cere sa se suprime din structura de arbore binar ordonat nodul cu aceasta cheie (daca nodul cu cheia exista in arbore) astfel incat dupa suprimare arborele sa ramana tot binar si ordonat.

Vom nota cu variabila pointer din nodul parinte al nodului de suprimat.

Se disting doua cazuri: primul caz este cel in care nodul de suprimat are cel mult un fiu:

 

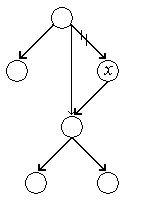
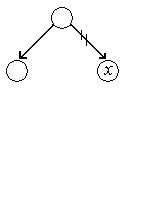
In acest caz variabila pointer se va modifica astfel incat sa indice unicul fiu al nodului (sau se va pune pe NULL daca nodul e nod frunza).

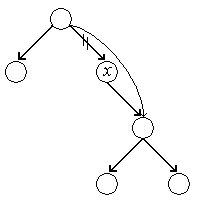
Cel de-al doilea caz este cazul in care nodul are doi fii. In acest caz, pentru ca dupa suprimare arborele sa ramana tot binar si ordonat, vom inlocui nodul cu predecesorul acestuia in inordine, sau cu succesorul acestuia in inordine (adica vom inlocui nodul cu cel mai din dreapta nod al subarborelui stang, sau cu cel mai din stanga nod al subarborelui drept).

Vom alege sa inlocuim nodul cu cel mai din dreapta nod al subarborelui stang, a carui cheie o vom nota cu . Dupa inlocuire nodul cu cheia va aparea de doua ori in arbore: pe locul sau initial si pe locul lui . Vom suprima nodul cu cheia din pozitia sa initiala conform celor spuse la primul caz, deoarece nu va avea mai mult de un fiu (sigur nu are fiu drept).

Determinarea nodului cu cheia poate fi realizata in modul urmator: se construieste o secventa de noduri care incepe cu fiul stang al nodului ce are cheia , alegand drept succesor pentru un nod in secventa fiul drept al acelui nod. Primul nod din secventa care nu va avea un fiu drept va fi nodul cu cheia pe care il cautam.

Se va copia cheia a nodului astfel determinat in locul cheii , (numai cheia, nu si adresele fiilor nodului cu cheia , pentru a nu distruge arborele), dupa care vom suprima nodul cu cheia conform celor spuse la cazul intai:

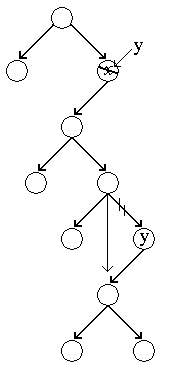
Functia C care realizeaza acest lucru este:

void supfd(int x, ref *r)

} /* supfd */

Functia ce va realiza suprimarea unui nod de cheie data dintr-un arbore binar ordonat va trebui sa ia in considerare ambele cazuri:

void suprimare(int x, ref *p)

}

} /* suprimare */

Arbori perfect echilibrati

Arborii perfect echilibrati au fost studiati tot in semestrul trecut, si i-am prezentat in detaliu in laboratorul 12 din caietul de laborator din semestrul trecut

Reamintim ca au fost introdusi in scopul organizarii unei colectii de noduri, fiecare nod avand o cheie de identificare de tip intreg, intr-o structura de tip arbore binar cu referinte multiple, singura conditie care se impune fiind ca arborele sa fie de inaltime minima.

Stim ca un arbore are inaltimea minima daca la fiecare nivel al arborelui se genereaza numarul maxim de noduri posibile, exceptie putand face doar ultimul nivel. Rezulta ca pentru a putea crea un arbore binar cu noduri de inaltime minima va trebui sa distribuim numarul de noduri pe care avem sa le introducem in mod egal pe stanga si pe dreapta fiecarui nod deja introdus. Distribuirea in mod egal a unui numar de noduri pe stanga si pe dreapta unui nod deja introdus se poate realiza printr-un proces recursiv care consta din:

se genereaza un nod ca nod radacina

se genereaza subarborele stang al acestuia avand numarul de noduri:

se genereaza subarborele drept al nodului radacina, cu un numar de noduri

Un arbore binar de inaltime minima astfel creat se mai numeste arbore perfect echilibrat (arbore total echilibrat).

Functia C care va realiza acest lucru:

ref Arbore(int N)

} /* Arbore */

Obs: Daca se doreste crearea unui arbore binar perfect echilibrat concret, din modul in care functioneaza functia Arbore rezulta ca nodurile arborelui trebuiesc transmise in preordine.

Programele:

Programul nr. 1:

#include<stdio.h>

#include<alloc.h>

#include<conio.h>

#include<stdlib.h>

#include<ctype.h>

#include<graphics.h>

#include<dos.h>

#define CALE 'C:BORLANDCBGI'

#define culoare MAGENTA

#define r 20

struct nod

;

typedef struct nod Tnod;

typedef Tnod *ref;

ref rad, q;

int x, timp=0;

void creare(void)

InArbore(x, &rad);

cleardevice();

preordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

gotoxy(1, 25);

printf('nMai doriti sa introduceti inca un nod? (D/N): ');

fflush(stdin); scanf('%c', &c); c=toupper(c);

}

} /* creare */

void InArbore(int x, ref *t)

else if(x<(*t)->cheie)

InArbore(x, &((*t)->st));

else InArbore(x, &((*t)->dr));

} /* InArbore */

void inordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*inordine*/

void preordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*preordine*/

void postordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*postordine*/

void Tip(ref anod, int nivel, int x1, int x2, int c1, int c2, char *s)

/*Tip*/

ref Loc(int x, ref t)

/* Loc */

void supfd(int x, ref *t)

} /* supfd */

void suprimare(int x, ref *p)

}

} /* suprimare */

Programul nr. 2:

#include<stdio.h>

#include<alloc.h>

#include<conio.h>

#include<stdlib.h>

#include<ctype.h>

#include<graphics.h>

#include<dos.h>

#define CALE 'C:BORLANDCBGI'

#define culoare MAGENTA

#define r 20

struct nod

;

typedef struct nod Tnod;

typedef Tnod *ref;

ref rad;

int nod_curent=1;

ref Arbore(int N);

void creare(void);

void Tip(ref anod, int nivel, int x1, int x2, int c1, int c2, char *s);

void inordine(ref rad, int nivel, int x1, int x2, int c1, int c2);

void preordine(ref rad, int nivel, int x1, int x2, int c1, int c2);

void postordine(ref rad, int nivel, int x1, int x2, int c1, int c2);

void main(void)

printf('Acest program permite crearea si vizualizarea naturalan');

printf('a unui arbore perfect echilibrat cu un nr dat de nodurin');

creare();

do

getch();

} while (op!='E');

closegraph();

} /*main*/

void creare(void)

printf('Introduceti nodurile in preordine:n');

rad=Arbore(N);

} /*creare*/

ref Arbore(int N)

else

while(scanf('%d', &(nod_nou->cheie))!=1)

nod_nou->st=Arbore(NS);

nod_nou->dr=Arbore(ND);

return nod_nou;

}

} /*Arbore*/

void inordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*inordine*/

void preordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*preordine*/

void postordine(ref rad, int nivel, int x1, int x2, int c1, int c2)

} /*postordine*/

void Tip(ref anod, int nivel, int x1, int x2, int c1, int c2, char *s)

/*Tip*/

void main(void)

printf('Acest program permite efectuarea tuturor operatiilor de baza asupran');

printf('unui arbore binar ordonat, cu vizualizarea naturala a arboreluin');

do

creare();

break;

case 'F': if(rad==NULL)

cleardevice();

preordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

gotoxy(1, 25);

printf('Cheia nodului cautat='); scanf('%d', &x);

nod_cautat=Loc(x, rad);

if(nod_cautat!=NULL)

printf('Nodul cu cheia %d se afla in arbore.n', nod_cautat->cheie);

else printf('Nodul cu cheia %d NU se afla in arbore.n', x);

break;

case 'A': cleardevice();

preordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

gotoxy(1, 25);

printf('Nodul pe care il vom insera are cheia ');

while(scanf('%d', &x)!=1)

InArbore(x, &rad);

preordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

break;

case 'D': if(rad==NULL)

cleardevice();

preordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

gotoxy(1, 25);

printf('Introduceti cheia nodului de sters: ');

scanf('%d',&x);

suprimare(x, &rad);

printf('nApasati o tasta');

getch();

cleardevice();

preordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

gotoxy(1, 25);

printf('Acesta este arborele in prezentn');

printf('Apasati o tasta');

break;

case 'I': cleardevice();

gotoxy(35, 29);

printf('AFISAREA IN INORDINEn');

timp=2000;

inordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

timp=0;

gotoxy(35, 29);

printf('ARBORELE ESTE COMPLET n');

printf('Apasati o tasta');

break;

case 'R': cleardevice();

gotoxy(35, 29);

printf('AFISAREA IN PREORDINEn');

timp=2000;

preordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

timp=0;

gotoxy(35, 29);

printf('ARBORELE ESTE COMPLET n');

printf('Apasati o tasta');

break;

case 'S': cleardevice();

gotoxy(35, 29);

printf('AFISAREA IN POSTORDINEn');

timp=2000;

postordine(rad, 0, 10, getmaxx(), getmaxx()/2, r);

timp=0;

gotoxy(35, 29);

printf('ARBORELE ESTE COMPLET n');

printf('Apasati o tasta');

break;

case 'E': cleardevice();

gotoxy(36,14);

printf('BYE - BYEn');

break;

default : printf('Optiune gresita!n');

printf('Apasati o tastan');

break;

}

getch();

cleardevice();

setbkcolor(BLACK);

gotoxy(2, 1);

} while (op!='E');

closegraph();

} /*main*/

Observatii:

Singura deosebire a acestor programe fata de modul in care au fost prezentate semestrul trecut este modul de afisare a arborelui, structura si meniul programelor ramanand nemodificate.

Primul program efectueaza toate operatiile de baza asupra arborilor binari ordonati (creare, cautarea, adaugarea si stergerea unui nod), in timp ce in cazul arborilor perfect echilibrati avem doar operatia de creare a arborelui cand cunoastem dinainte numarul de noduri. Operatia de inserare va face tema laboratorului urmator, iar operatia de stergere a unui nod va fi studiata in laboratorul nr. 3, insa pentru efectuarea acestor operatii nu vom mai pune conditia ca arborele sa fie perfect echilibrat, ci numai echilibrat dupa inaltime.

In cazul arborilor binari ordonati noul nod se insereaza chiar daca exista deja in arbore un nod cu aceeasi cheie. In acest caz se considera ca noul nod are cheia mai mare decat cheia nodului deja existent.

Nodurile arborilor trebuie introduse in cazul arborilor binari ordonati in preordine sau pe nivele, iar in cazul arborilor perfect echilibrati numai in preordine.

In cadrul primului program, in toate functiile am prezentat si arborele (pentru verificare) si de aceea aveam nevoie de desenarea instantanee a acestuia, in timp ce pentru afisarea arborelui in inordine/preordine/postordine dorim sa fie desenate nodurile arborelui mult mai incet, pentru a vedea ordinea in care apar acestea, acesta fiind motivul pentru care am introdus variabila globala timp.