UNIVERSITATEA TEHNICA DIN CLUJ-NAPOCA

Facultatea de Automatica si Calculatoare

Catedra de Automatica

Memoriu tehnic

Consideratii teoretice generale

Filtrarea numerica a semnalelor

Sistemele de reglare numerica realizeaza, inainte de reglare, conversia sub forma numerica a semnalelor de la iesirea traductoarelor si, dupa calcularea comenzii, genereaza iesiri sub foma analogica.

Prelucrarea primara a datelor se poate face atat prin metode analogice cat si prin metode numerice sau combinat, prin ambele metode. Indiferent de modul de prelucrarea primara a datelor, este necesara alegerea unei perioade de esantionare si de conversie analognumerica. Pentru un semnal lent variabil in timp, la care conversia analognumerica se face la momente de esantionare fixate prin program, reconstituirea semnalului prin metode de interpolare poate da rezultate precise pentru precizia aleasa.

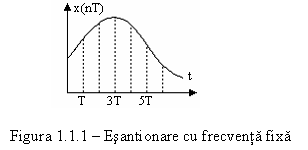
Daca semnalul supus conversiei poate avea variatii rapide in timp, atunci esantionarea la intervale constante de timp (Fig. 1.1.1) nu poate oferi rezultate acceptabile, deoarece se pot pierde informatii din evolutia semnalului (Fig. 1.1.2). Pe de alta parte micsorarea perioadei de esantionare poate duce la cresterea inacceptabila a volumului de date care trebuie prelucrat. Pentru a se evita acest dezavantaj se poate recurge la prelucrarea primara a semnalelor prin metode analogice.

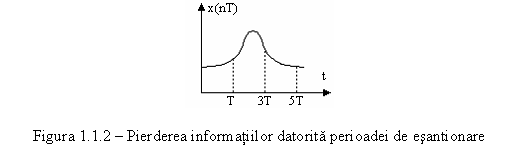
Daca semnalul analogic are o variatie brusca in timp si aceasta nu poate fi prinsa prin esantionarea cu o perioada constanta, atunci se poate recurge la utilizarea unui circuit electronic care sa declanseze conversia pentru o anumita panta de variatie a semnalului, evitandu-se astfel pierderea unei variatii importante din semnal.

La sistemele numerice influenta zgomotelor este mai periculoasa decat in cazul sistemelor continue de reglare care, pot asigura eliminarea efectelor semnalelor de frecventa ridicata datorita proprietatii de filtru trecejos pe care o au. In cazul sistemelor de reglare numerica, masurarea unei valori alterate sensibil de zgomot in momentul esantionarii, constituie o informatie eronata (in absenta unor masuri de filtrare), este considerata valabila si prelucrata ca atare de regulatorul numeric, rezultand o functionare incorecta a sistemului.

Conversia analognumerica devine o problema atunci cand semnalul de intrare este supus unor zgomote, si se impune utilizarea unui filtru la intrare. Prin introducerea acestui filrtru se urmareste scaderea in cat mai mare masura a influentei perturbatiilor asupra semnalului convertit. Cateva tipuri de filtre des utilizate sunt: filtrul de tip intarziere de ordinul I, filtrul cu banda constanta, filtrul cu banda adaptiva, filtrul cu factor de pastrare variabil sau filtrul cu mediere.

Filtrarea tip intarziere de ordinul I

Este foarte des folosita in cazul sistemelor continue. Filtrul de tip intarziere de ordinul I este de fapt un filtru trecejos si asigura o filtrare de tip exponential (la un semnal de intrare de tip treapta raspunsul este o exponentiala).[4]

Functia de transfer a unui asemenea element este:

(1.2.1.1.1)

unde, y_fI este semnalul de iesire din filtru, u_fI este semnalul de intrare in filtru, iar T_fI este constanta de timp a filtrului (se observa ca factorul de amplificare este unitar).

Din relatia (1.2.1.1.1) rezulta:

de unde prin trecerea in domeniul timp se obtine:

Daca se accepta faptul ca se poate aproxima derivata cu diferente finite se poate scrie:

Considerand ca Dt este chiar T_e (perioada de esantionare a sistemului discret) si ca :

(1.2.1.1.5)

rezulta:

(1.2.1.1.6)

Se obtine astfel o noua forma pentru functia de transfer de la care am pornit:

(1.2.1.1.7)

Aceasta din urma relatie (1.2.1.1.7) cuprinde aproximatia derivatei, de care am pomenit mai sus si datorita acestui fapt se scapa informatie (derivata continua contine informatii asupra tendintei viitoare de evolutie, pe cand echivalentul discret inglobeaza doar informatii referitoare la valoarea curenta y_k si valoarea anterioara y_{k - 1}).

Din relatia (1.2.1.1.7), prin efectuarea unor calcule se obtine dependenta:

(1.2.1.1.8)

Se observa ca, daca notam , cu lI[0, 1] rezulta o relatie de forma:

(1.2.1.1.9)

In relatia (1.2.1.1.9) acest l poate fi privit ca un factor de mentinere a valorii vechi. Daca se facea o notare inversa, atunci spuneam ca l este factor de uitare.

Intensitatea filtrarii depinde de valoarea aleasa pentru coeficientul l. Daca l  1, respectiv T _fI >> T _e filtrarea este foarte puternica, deoarece valoarea y _f, k ramane apropiata de valoarea anterioara y _f, k1, deci influenta zgomotelor este redusa; daca l  0, respectiv T_fI << T _e filtrarea este foarte slaba. Problema care se pune este ca in primul caz (l 1), datorita filtrarii puternice nu se pot urmarii semnale puternic variabile, ci numai lent variabile.

Filtrarea cu banda constanta

In acest caz se stabileste o limita constanta L pentru diferenta dintre valoarea marimii masurate u _k si valoarea de la tactul anterior a acestei marimi y_k-1.

Considerand ca elementul de filtrare de ordinul I are la intrare marimea masurata u _k si la iesire marimea filtrata y _k, algoritmul de filtrare cu banda constanta prevede urmatoarele conditii:

daca:

(1.2.1.2.1)

adica, valoarea masurata nu este afectata de zgomote, filtrarea nu are loc si se alege:

y _k = u _k

daca:

(1.2.1.2.3)

are loc depasirea benzii stabilite L si se efectueaza filtrarea corespunzatoare unui filtru de tip intarziere de ordinul I.

Filtrarea cu banda adaptiva

Este indicata in cazul semnalelor cu tendinte de variatie abrupta in timp. In locul unei valori constante a benzii (cazul anterior), este folosita o banda variabila, conform relatiei:

(1.2.1.3.1)

unde: L _k este valoarea benzii la pasul k;

L este valoarea minima posibila a benzii, pentru J _k = 0;

J _k este o variabila care ia valori dupa o anumita lege (expusa in continuare).

In cazul filtrului cu banda adaptiva intervin doi algoritmi: unul de filtrare si unul de adaptare a benzii. Algoritmul de filtrare prevede urmatoarele conditii:

daca:

(1.2.1.3.2)

valoarea masurata nu este afectata de zgomote, filtrarea nu are loc si se alege:

y_k = u_k (1.2.1.3.3);

daca:

(1.2.1.3.4)

se alege:

y_k = y_k1  L _k

semnul +/ fiind determinat de semnul diferentei y_k  y _k1.

Algoritmul de adaptare este definit prin urmatoarele trei ipoteze:

daca:

(1.2.1.3.6)

atunci banda se contracta si se alege:

J_k = J_k1 - A (1.2.1.3.7);

Constanta A este pozitiva si in practica poate sa ia valorile din tabelul 1.2.1.3.1:

daca:

(1.2.1.3.8)

atunci banda ramane constanta si se alege:

J_k = J_k1 (1.2.1.3.9);

daca:

(1.2.1.3.10)

atunci banda se expandeaza si se alege:

J_k = J_k1 + A (1.2.1.3.11);

Avantajul filtrarii cu banda adaptiva consta in faptul ca la o prima masurare in afara benzii nu are loc filtrarea, consideranduse ca masurarea este afectata de zgomote. Daca insa persista o masurare in afara benzii, atunci se efectueaza expandarea, cu scopul ca noua banda sa includa urmatoarea masurare ca o valoare valida, corespunzatoare unei tendinte de variatie; in mod similar se realizeaza contractarea benzii.

Filtrarea cu banda adaptiva introduce astfel o pondere mai mare in considerarea evolutiei anterioare, fiind mai putin sensibila la zgomote si urmarind in conditii mai bune tendintele de variatie ale semnalului de intrare.

Filtrarea prin mediere

Pentru micsorarea influentei zgomotelor se foloseste si filtrarea prin medie aritmetica a unui numar de valori masurate, care poate fi egal cu 2 la o putere intreaga, astfel incat divizarea sumei prin numarul de valori masurate sa poata fi facuta simplu printro deplasare la dreapta pe biti.

Influenta zgomotelor este cu atat mai redusa cu cat medierea se extinde pentru un numar mai mare de valori masurate, crescand insa timpul necesar realizarii sumei adica, perioada de esantionare cu care se poate lucra in sistem.

1.2. Regulatoare numerice

Regulatorul automat are rolul de a prelua operational semnalul de eroare, obtinut in urma comparatiei liniar-aditive a semnalului de intrare r si a semnalului de reactie y in elementul de comparatie si de a elabora la iesire un semnal de comanda u pentru elementul de executie. Informatiile curente asupra desfasurarii procesului tehnologic se obtin cu ajutorul traductorului de reactie si sunt preluate de regulatorul automat in conformitate cu o anumita lege care defineste algoritmul de reglare automata.

Algoritmii de reglare (legile de reglare) conventionali utilizati frecevnt in reglarea proceselor tehnologice sunt de tip proportional-integral-derivativ.

Implementarea unei anumite legi de reglare sepoate realiza print-o varietate destuld e larga a constructiei regulatorului, ca regulator electronic, pneumatic, hidraulic sau mixt.

Chiar si in cadrul aceleiasi categorii constructive se pot realiza variante diferite, fiecare solutie oferind anumite avantaje din punct de vedere al preciziei de realizare a legii de reglare, apretului , a sigurantei in functionare si a flexibilitatii in exploatare.

Structura unui sistem de reglare numerica (fig. 1.2.2.1) evidentiaza faptul ca un asemenea sistem este hibrid din punct de vedere al informatiei pentru ca se vehiculeaza atat informatie sub forma analogica cat si sub forma numerica.

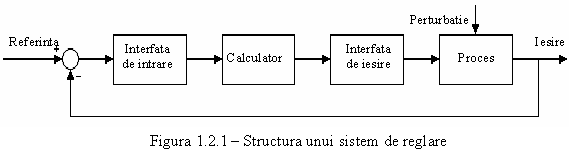
Din figura 1.2.1 se remarca doua blocuri: interfata de intrare si interfata de iesire, elemente despre care vom discuta in continuare.

Interfata de intrare care, are rolul de a discretiza informatia din proces prin operatii de esantionare si cuantizare. Acest bloc cuprinde un element de esantionare si un element de cuantizare (convertor numericanalogic) asa cum se vede in figura 1.2.2.

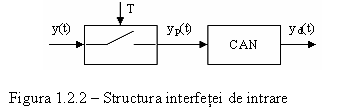
Figura 1.2.3 prezinta etapele prin care trece un semnal de intrare continuu pentru a se transforma intr-un semnal numeric astfel:

graficul a) prezinta semnalul (informatia) continuu;

graficul b) prezinta semnalul rezultat in urma esantionarii;

graficul c) prezinta semnalul numeric rezultat.

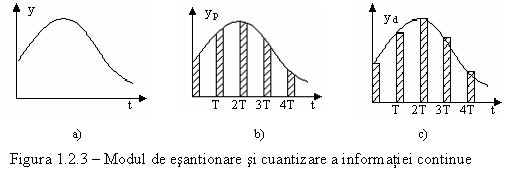
Iesirea y _p(t) din circuitul de esantionare este reprezentata sub forma unei succesiuni de impulsuri modulate in amplitudine, de perioada T. Durata impulsurilor este constanta si egala cu p (latimea suprafetei hasurate), fiind determinata de performantele elementului de esantionare (de ex. viteza de comutatie). Cuantizarea informatiei, rezultata in urma unei trunchieri sau rotunjiri, se realizeaza cu ajutorul convertorului analognumeric.

Interfata de iesire este realizata cu un extrapolator. Elementul de retinere (extrapolatorul) are rolul de a reface semnalul continuu, avand in vedere ca elementul de executie (cuprins in proces) este un element cu functionare continua. Cel mai simplu tip de extrapolator este elementul de esantionare retinere de ordinul zero(ER0), a carui structura este prezentata in figura 1.2.4.

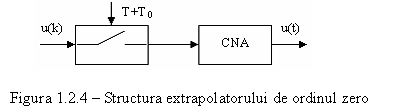
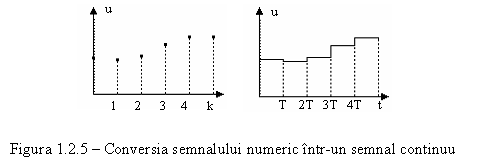
Figura 1.2.5 pune in evidenta semnalul numeric (valori numerice) si semnalul analogic obtinut prin extrapolare. Trecerea de la un tip de semnal la altul se realizeaza cu un extrapolator de ordinul zero care, mentine constanta valoarea functiei la iesire, pe parcursul unei perioade de esantionare. Daca se considera aplicat la intrare un impuls unitar, raspunsul acestui element de extrapolare se poate calcula ca diferenta a doua trepte unitare, iar functia de transfer asociata acestuia este in relatia (1.2.2.1):

(1.2.1)

Se observa ca in figura 1.2.2.4 se foloseste o perioada de esantionare la iesire (T+T₀). Diferenta dintre perioada de esantionare la iesire si perioada de esantionare a informatiei de intrare este determinata de necesitatea prelucrarii informatiei pe cale numerica. In cazul prelucrarii numerice a informatiei cu viteze ridicate se poate admite ca cele doua circuite de esantionare sunt sincrone.

Metode de discretizare

Pentru a caracteriza functionarea sistemelor cu esantionare se considera modelul unui circuit de esantionare ideal (p << T):

k = 0, 1, 2, (1.2.1.1)

Din definitie, relatia (1.2.2.1.1), se observa ca circuitul de esantionare ideal furnizeaza la iesire o succesiune de impulsuri modulate in amplitudine, echidistante.

Introducand notatia z = e ^sT, se poate defini transformata Z a unei functii discrete sub forma data de relatia (1.2.2.1.2):

(1.2.1.2)

O posibilitate de a obtine modelul discret al unei functii continue consta in a discretiza functia continua printro procedura de discretizare cum ar fi: metoda dreptunghiului, metoda trapezelor, metoda RungeKutta, proceduri care permit aproximarea integralei functiei respective prin intermediul unor relatii de calcul de tipul sumei sau diferentei.

Discretizarea prin metoda dreptunghiului

Aceasta metoda permite obtinerea echivalentului discret al unei functii continue pornind de la relatia de aproximare a integralei prin relatia (1.2.2.1.1.1):

(1.2.1.1.1)

sau:

(1.2.1.1.2)

unde u(k) reprezinta functia de intrare, iar y(k) functia de la iesirea unui integrator cu ecuatia matematica de forma descrisa de relatia (1.2.1.1.3):

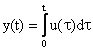(1.2.1.1.3)

O structura a unui astfel de integrator poate fi cea din figura 1.2.1.1.1

Folosind aceasta metoda de discretizare se pot obtine modele matematice sub forma ecuatiilor cu diferente.

1.2.1.2. Discretizarea prin metoda trapezelor

Prin intermediul acestei metode se aproximeaza integrala unei functii prin relatia (1.2.1.2.1):

(1.2.1.2.1)

sau:

(1.2.1.2.2)

Desigur, in acest caz aproximarea este mult mai buna, dar problema care apare este cresterea volumului calculelor.

1.2.2. Regulatorul P

Este cel mai simplu tip de regulator. Functia de transfer este data de relatia :

unde c(t) este comanda, e(t) este eroarea, iar K este valoarea coeficientului proportional.

Din formula se poate scrie :

care trecuta in domeniul discret este (1.2.2.3):

Aceasta ultima formula (1.2.2.3) poate fi interpretata astfel: valoarea curenta a comenzii este valoarea curenta a erorii inmultita cu constanta de proportionalitate a regulatorului. Relatia este de fapt ecuatia care descrie functionarea regulatorului P numeric.

1.2.3. Regulatorul PI

Acesta este cel mai utlizat tip de regulator deoarece nu cere o putere de calcul prea mare si asigura o eroare stationara la pozitie nula. Ecuatia de functionare in domeniul timp poate fi scrisa sub forma (1.2.3.1):

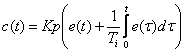
Aceasta ecuatie trecuta in domeniul discret arata (1.2.3.2):

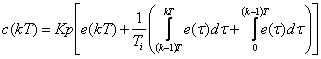
Pasul urmator spre obtinerea unei relatii care poate fi calculata numeric este aproximarea integralei cu una din cele doua metode prezentate in Capitolul 1.2.2.1. Vom folosi aproximarea prin metoda trapezului pentru ca ofera un rezultat mai apropiat de cel real, chiar daca va necesita un timp de calcul mai mare. Formula pe care o vom folosi este :

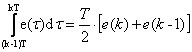(1.2.3.3)

Prin inlocuirea in relatiea de definitie a integralelor cu aproximarea se obtine relatia (1.2.3.4):

(1.2.3.4)

care mai poate fi scrisa sub forma (1.2.3.5):

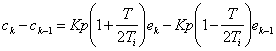
unde, prin c_k s-a notat c(kT), iar prin c_k-1 s-a notat c[(k-1)T].

Se obtine astfel o relatie de calcul a valorii curente a comenzii functie de valoarea anterioara a comenzii si de valoarea curenta respectiv anterioara a erorii (1.2.3.6):

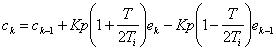
Aceasta din urma relatie defineste functionarea regulatorului PI numeric.

1.2.4. Regulatorul PID

Relatia care reprezinta regulatorul PID ideal este prezentata in continuare :

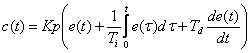
Pentru a trece in domeniul discret este necesara introducerea aproximarii folosite pentru efectul derivativ. Admitem ca se poate scrie derivata sub forma diferentei finite. Astfel vom avea relatia (1.2.4.2):

Ultima parte a relatiei (1.2.4.2) nu se foloseste pentru ca nu are sens tehnic, neavand posibilitatea sa aflam valori viitoare ale erorii.

Relatia pentru regulatorul PID poate fi scrisa ca in (1.2.4.3):

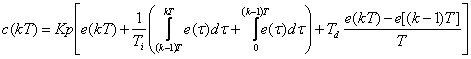
Aplicand acum formula de la metoda trapezului va rezulta (1.2.4.4):

(1.2.4.4)

si

(1.2.4.5)

unde,

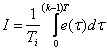
Din cele doua relatii ale c_k si c_k-1 prin scadere se obtine (1.2.4.7):

Din aceasta ultima relatie (1.2.4.7) se poate obtine o relatie a valorii comenzii in functie de valoarea anterioara a comenzii si de valori ale erorii (curenta si anterioare) :

Relatia (1.2.4.8) descrie functionarea regulatorului PID ideal numeric.

1.2.5. Regulatorul PD

In lucrarea de fata s-a implementat regulatorul PD ideal, pentru ca este realizabil doar pe cale numerica. Relatia matematica folosita la descrierea functionarii acestui tip de regulator este (1.2.5.1):

Aceasta relatie (1.2.5.1) poate fi rescrisa, tinand cont de aproximarea derivatei cu diferente finite, astfel :

Prin inlocuirea kT = k si (k - 1)T = k - 1 se va obtine o relatie asemanatoare relatiilor de la celelalte regulatoare (1.2.5.3):

Aceasta ultima relatie (1.2.5.3) prezinta legatura dintre valoarea actuala a comenzii si valoarea curenta respectiv precedenta a iesirii, fiind, deci, relatia care defineste functionarea regulatorului PD numeric.

1.3. Circuite logice

Circuitele logice combinationale, CLC, sunt un caz particular al sistemelor secventiale finite sau al automatelor finite, numite automate de grad 0.

Circuitele logice combinationale se caracterizeaza prin faptul ca variabilele de iesire sunt independente de timp si de starea interna, fiind determinate numai de variabilele de intrare (starea variabilelor de intrare la momentul considerat).

Legatura dintre starea iesirii si starea intrarii unui CLC este realizata de functia de transfer.

Figura 1.3.1 Structura unui circuit combinational

Oricare functie de iesire y (y₁, y₂,., y_m) este functie de toate variabilele de intrare (x₁, x₂,., x_n). Un CLC se poate descrie astfel:

y₁ = f₁(x₁, x₂,., x_n)

y₂ = f₂(x₁, x₂,., x_n)

y_m = f_m(x₁, x₂,., x_n)

Functiile se vor exprima in forma canonica disjunctiva FCD sau in forma canonica conjunctiva FCC.

Independenta fata de timp presupune ca o data cu modificarea variabilelor de intrare se modifica simultan si variabilele de iesire. Din punct de vedere practic, datorita intarzierilor produse de circuitele logice si de conexiuni, modificarea simultana nu este posibila. Ca urmare, pe durata procesului tranzitoriu de stabilire a variabilelor de iesire, vectorul iesirilor poate lua valori intermediare diferite de valoarea finala, ceea ce conduce la fenomenul de hazard combinational, de care trebuie sa se tina cont la proiectarea unui sistem numeric.

In general, la circuitele logice combinationale, vom face abstractie de proprietatile fizice ale portilor logice, de faptul ca un impuls teoretic difera de unul real. Vom analiza aceste fenomene doar in cazul hazardului combinational.

1.3.1.Analiza circuitelor logice combinationale

In cadrul analizei CLC se pleaca de la cunoasterea schemei logice a circuitului si se urmareste stabilirea functionarii acestuia. Stabilirea expresiei variabilei de iesire se face de la intrare la iesire, urmarind transformarile variabilelor de intrare.

Definim ca numar de nivele al unui CLC numarul maxim de porti dintre intrari si iesiri. Numerotarea nivelelor se face de la iesire inspre intrare.

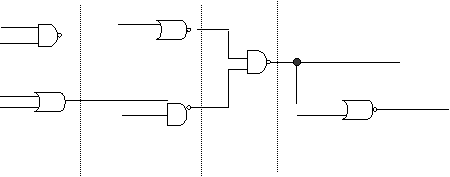x₅

x₁

x₂

y₁

x₃

x₄  y₂

x₆ x₇

4 3 2 1

Figura 1.3.1.1 Structura unui circuit combinational cu 4 intrari si 2 iesiri

Circuitul logic combinational din exemplu are 4 nivele.

Exista si urmatoarea situatie de legaturi intre porti:

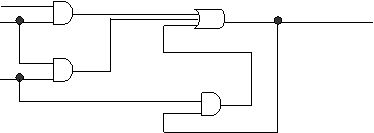x₁  y

x₂

x₃

Figura 1.3.1.1 Structura unui circuit combinational cu 3 intrari si 1 iesire

Acest circuit are si legaturi inverse. Ultimele porti nu pot fi numerotate, deci circuitul nu este un CLC.

In CLC sunt admise legaturile inverse (iesirea unei porti dintr-un nivel inferior sa fie dusa la intrarea unei porti dintr-un nivel superior) cu conditia ca definitia CLC sa fie respectata.

1.3.2. Algoritm de determinare a legaturilor inverse in CLC

a. Se numeroteaza toate portile logice care au ca intrari un subset din multimea variabilelor de intrare ale circuitului logic (de la 1 la k);

b. Se numeroteaza de la k+1 portile care au ca intrari fie intrari ale circuitului, fie iesiri ale portilor numerotate la punctul a. Daca am reusit sa numerotam toate portile circuitului logic, acesta este fara legaturi inverse si este circuit combinational. Daca nu am reusit numerotarea tuturor portilor logice, circuitul este de tip secvential.

1.3.3.Circuite combinationale uzuale (specializate)

Multiplexoare

Multiplexoarele sunt CLC care permit trecerea datelor de pe una din intrari la o iesire unica. Selectia intrarii se face printr-un cuvant de cod de selectie numit si adresa.

Figura 1.3.3.1 Structura unui multiplexor cu n intrari si m selectii

Cu m linii de selectie se pot selecta 2^m intrari. Functia realizata de iesire este:

y = I_k ,

unde k este numarul de combinatii

k = s_m-1 2^m-1 + . + s₀

Aplicatiile cele mai importante ale MUX sunt la selectia secventiala a datelor, conversia paralel-serie a datelor, sisteme de transmisie a datelor pe un singur canal, implementarea circuitelor logice combinationale cu o singura iesire.

In cintinuare sunt prezentate exemple de multiplexoare cu diferite semnale de intare:

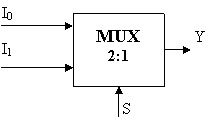
Figura 1.3.3.2 Structura unui multiplexor cu 2 intrari si 1 selectie

Multiplexorul de tip 2:1 are 2 semnale de intrare, I₀ si I₁, un semnal de selectie s si o iesire y. In functie de semnalul de selectie avem pentru iesire: y = I₀ s + I₁ s.

s = 0 y = I₀

s = 1 y = I₁

Deci multiplexorul lasa sa treaca spre iesire semnalul de pe acea linie de intrare

corespunzatoare ale lui s.

Figura 1.3.3.3 Structura unui multiplexor cu 4 intrari si 2 selectii

Multiplexorul de tip 4:1 are 4 semnale de intrare, 2 semnale de selectie si un semnal de iesire. Iesirea va fi:

y = I₀ s₀ s₁ + I₁ s₀ s₁ + I₂ s₀ s₁ + I₃ s₀ s₁

Exista multiplexoare de tip 8 : 1, 16: 1, 32 : 1. Multiplexoarele integrate au disponibile atat iesirea adevarata cat si cea negata. Ele au si o intrare de "Enable" pentru validare, care permite o functie SI suplimentara.

Demultiplexoare

Demultiplexoarele sunt CLC care permit transmiterea datelor de pe o intrare de date comuna pe una din iesirile selectate. Selectarea iesirii se face cu ajutorul unui cuvant de cod de selectie numit si adresa.

Figura 1.3.3.4. Structura unui demultiplexor cu n iesiri si m selectii

Cu m linii de selectie se pot selecta 2^m iesiri. Functiile de iesire sunt:

y₀ = s_m-1 s₀ I

y₁ = s_m-1 s₀ I

y₂^m = s_m-1 s₀ I

Comparatoare numerice

Comparatoarele numerice sunt CLC care permit determinarea valorii relative a doua numere binare. Comparatoarele pot fi de 1 bit sau de mai multi biti.

Exemplu: Comparator pe 1 bit

Figura 1.3.3.5 Structura unui comparator numeric

Functiile de iesire sunt:

y₁ = A_i B_i  pentru A_i < B_i,

y₂ = A_i + B_i pentru A_i = B_i

y₃ = A_i B_i  pentru A_i > B_i

Acest circuit constituie celula de baza pentru compararea numerelor cu mai multi biti

Hazardul combinational

Datorita intarzierilor produse de circuitele logice si de firele de legatura ale unui CLC se poate ca starea iesirii circuitului in momentul modificarii starii variabilelor sa nu coincida cu valoarea functiei corespunzatoare valorii intrarilor in momentul considerat. Pentru timp scurt circuitul are o comportare gresita, numita hazard.

Exemplu

f(x₁,x₂,x₃) = x₁ x₃ + x₂ x₃

x₁  D f'

x₃  g D

f

x₂  D

x₃ h

In practica intarzierile D D D ale portilor SI-NU nu sunt egale, de aceea poate sa apara hazardul combinational si cand se pune conditia ca doar o singura variabila de intrare sa se modifice la un moment dat.

Hazardul apare atunci cand starea intrarilor x₁x₂x₃ se modifica de la 010 la 011 sau invers.

x₁

x₂

x₃

D

g

D

h

f'

f

D

t_r

D > D desi starea ar trebui sa fie nemodificata.

Dupa timpul de reactie t_r = D D va apare la iesire un impuls negativ de durata Dt = D D si in aceasta durata iesirea ia o valoare incorecta.

Eliminarea hazardului static se poate face in cazul in care se impune ca la un moment dat sa se modifice starea unei singure variabile de intrare. Pentru realizarea functiei se considera si unii termeni redundanti din diagrama Karnaugh, astfel incat oricare doi de 1 aflati in casute adiacente in diagrama sa fie inclusi cel putin intr-un contur luat in considerare la sinteza schemei.

Pentru exemplul dat se va introduce in expresia functiei termenul x₁x₂.

f = x₂ x₁ + x₃ x₁ + x₃ x₂

x₁ g D

x₃

f'

x₂ h D D f

x₃

x₁ i Dt

x₂

x₁

x₂

x₃

D

g

D

h

i

f'

f

Observatii

Hazardul static poate sa apara si cand D > D , la schimbarea 011 in 000.

Proiectarea unui CLC cand se schimba mai mult decat o singura variabila de intrare la un moment dat, fara sa apara hazard, este mai dificila sau chiar imposibil de realizat (hazard de functie).

Eliminarea sigura a hazardului se poate face luand in considerare iesirea circuitului dupa un interval de timp mai mare decat intarzierea maxima din circuit.

1.3.4. Sinteza CLC cu PLA

PLA (Programmable Logic Array) este un CLC cu doua nivele de logica programabila, o matrice de porti SI si o matrice de porti SAU. PLA este de fapt o structura universala, extinsa, de implementare cu 2 nivele de porti logice. Ambele matrici sunt programabile, in procesul de fabricatie sau de catre utilizator, conform aplicatiei concrete. PLA este o structura mobila si se utilizeaza eficient pentru sisteme cu mai mult de 8 variabile de intrare.

Deoarece la PLA sunt programabile ambele nivele, implementarea se face pornind de la termenii elementari ai functiei, obtinuti prin minimizarea ei.

Reprezentarea schematica a PLA cu n intrari, m iesiri si p termeni elementari realizabili este:

x₁  conexiune programabila

x₂

x_n

Matrice

SI

1 p

1 f₁

conexiune Matrice

programabila SAU

f_m

m

conexiune programabila

CS

Figura 1.3.4.1 Structura PLA schematic

Avantajele implementarii cu PLA fata de implementarea cu ROM se refera la posibilitatea programarii matricei SI si a complementarii variabilelor de iesire (variabilele de iesire pot fi programate individual ca active pe 0 sau pe 1).

Aplicatii ale PLA sunt la:

- microprogramare;

- conversii de cod;

- generare de caractere;

- realizare de tabele de functii;

- implementarea automatelor secventiale.

Observatie. Exista circuite integrate cu grad si mai mare de integrare (VLSI) utilizate in implementare. Amintim dintre acestea FPGA (Field Programmable Gate Array).

1.3.5.Circuite logice secventiale

Circuitele logice secventiale, CLS, sunt automate de ordinul 1. Se obtin din automatele de ordinul 0 (CLC) prin introducerea unor reactii (legaturi inverse). Sunt alcatuite din circuite logice combinationale si elemente de memorare binara.

Semnalele de iesire ale CLS depind atat de combinatia semnalelor aplicate pe intrari cat si de starea circuitului. Un CLS este caracterizat printr-o secventa a semnalelor de iesire si o secventa a starilor elementelor de memorie, pentru fiecare secventa a semnalelor aplicate pe intrarile circuitului.

Dupa modul de functionare (modul de transmitere a semnalelor) exista 2 categorii principale de CLS:

asincrone - comportarea este determinata de aplicarea pe intrari a semnalelor in momente oarecare; starea circuitului depinde de ordinea in care se schimba semnalele;

sincrone - comportarea este determinata de aplicarea pe intrari a semnalelor in momente discrete, bine determinate in timp; sincronizarea se realizeaza cu ajutorul unor impulsuri date de un generator de tact (ceas).

Exemple de CLS: bistabili, numaratoare, registre, memorii RAM.

Circuite basculante bistabile

Definitie. Circuitele basculante bistabile (CBB sau bistabili) sunt circuite logice secventiale care au doua stari stabile distincte. Trecerea dintr-o stare in alta se face la aplicarea unei comenzi din exterior.

Caracteristica principala a CBB este ca sunt sisteme cu memorie (elemente de memorie binara). Un bistabil poate pastra un timp nedefinit informatia binara si in acelasi timp starea sa poate fi citita in orice moment. Se asociaza uneia dintre cele 2 stari ale bistabilului functia de memorare a cifrei binare 1 si celei de a doua stari functia de memorare a cifrei binare 0. Bistabilul are 2 iesiri, una care pune in evidenta cifra binara memorata, numita iesire adevarata si a doua, care pune in evidenta valoarea negata a cifrei binare memorate, denumita iesire negata.

1.4. CPLD-uri( complex programmable gate device)

1.4.1. Introducere in CPLD-uri( complex programmable gate device)

Utilizarea pe scara larga a calculatoarelor a dus la necesitatea studierii lor globale, ca dispozitive de prelucrare a informatiei reprezentata simbolic, in scopul descoperirii de noi resurse de dezvoltare sau a limitarii acestor masini.

Studiul, pentru a fi general, trebuie sa plece de la caracteristici comune - teoria automatelor realizeaza acest studiu al posibilitatilor si limitarilor dispozitivelor de prelucrare a informatiei, folosind un model abstract al tuturor dispozitivelor, model care imita activitatea si aspectul functional al acestora. Acest model abstract de numeste automat.

Primele circuite logice programabile au fost produse de corporatia Advanced Micro Devices (AMD). Circuitele logice programabile cunoscute si sub forma acronimului PLD(Programmable Logic Device), sunt circuite integrate care contin un numar mare de poti sau celule a caror interconexiune poate fi configurata sau programata pentru a implementa orice functie combinationala sau secventiala dorita. Pentru programarea circuiteleor PLD se utilizeaza doua tehnici: programarea prin masti , care se efectueaza in timpul procesului de fabricatie si programarea de catre utilizator pentru care se utilizeaza echipamente de programare cu costuri reduse. Multe circuite PLD pot fi reprogramate de utilizator de multe ori, motiv pentru care sunt avantajoase pentru realizarea prototipurilor unui nou produs.

Coneziunile programabile intre elemntele logice ale unui PLD contin comutatoare realizate de obicei cu tranzistoare sau antifuzibile(uneori fuzibile). Portile logice programabile ale unui circuit PLD pot fi reprezentate in mod simplificat.

O retea logica programabila PLA(Programmable Logic Array)este similara ca si concept cu o memorie ROM cu exceptia faptului ca nu realizeaza decodificarea concreta a varibilelor si nu genereaza toti mintermii. Decodificatorul este inlocuit cu o retea de porti logice SI care poate fi programata pentru a genera termenii produs ai variabilelor de intrare. Termenii produs sunt apoi conectati in mod selectiv cu porti SAU pentru a genera suma termenilor produs pentru functiile booleene necesare. Un circuit PLA poate implementa in mod direct un set de functii logice exprimate printr-un tabel de adevar. Fiecare intrare pentru care valoarea functiei este adevarata necesita un termen produs sia cestuia ii corespunde o linie de porti SI din primul etaj al circuitului PLA. Un circuit PLA are doua caracteristici care determina o implementare eficienta a unui set de functii logice Prima este ca singurele intrari din tabelul de adevar care necesita porti logice sunt cele carora le corespunde o valoare adevarata pentru cel putin o iesire. A doua este ca un termen produs va avea o singura intrare in circuitul PLA chiar daca temenul produs este utilizat in mai multe iesiri.

Circuitele CPLD sunt o modalitate de extindere a circuitelor PLD. In figura de mai jos este prezentata schema unui astfel de circuit CPLD traditional:

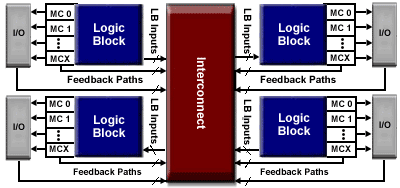
Figura 1.4.1.1- Schema unui CPLD

1.4.2.CoolRunner 2

In continuare se prezinta circuitele din seria COOLRUNNER . Din aceasta serie fac parte doua circuite: COOLRUUNER XPLA3(3,3V) si COOLRUUNER II(1,8V).

Circuitul COOLRUNNER II este un circuit din familia CPLD-urilor care are urmatoarele avantaje: putere mica, costuri mici, performanta ridicata si design flexibil.

Se poate evidentia mai multe aspecte ale acestui dispozitiv : COOLRUNNER II in cele ce urmeaza.

Arhitectura unui COOLRUNNER II

Arhitectura unui COOLRUNNER II este asemanatoare cu a unui CPLD clasic, combina macrocelulele in functiile bloc interconecate cu AIM(advanced interconecting matrix). Blocurile de functie folosesc o configuratie PLA (retea logica programabila). Blocul functie se ataseaza pinilor si se interconecteaza unele cu altele prin intermediul matricii interne de interconectare. Fiecare bloc de functie contine 16 celule cu 40 de intrari pentru semnale. Toate blocurile de functii care apartin acestui sistem sunt identice .

Rezultatul acestei arhitecturi este un model care are o sincronizare variabila. Software-ul utilizat incearca sa utilizeze cat mai multe functii in blocul de functie functiile nu necesita folosirea unui ceas comun , a unui set/reset si de asemenea nu necesita o iesire comuna. In figura de mai jos este prezentata arhitectura unui COOL RUNNER II:

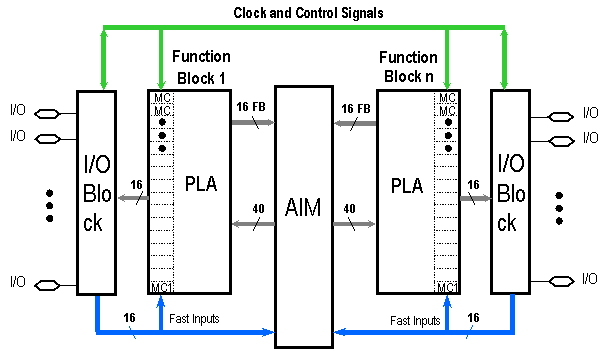
Figura 1.4.2.1.1 Arhitectura unui COOLRUNNER II

In figura de mai jos este prezentata arhitectura unui bloc de functii:

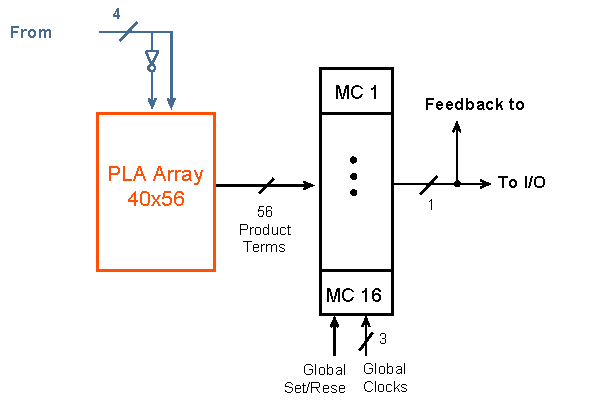
Figura 1.4.2.1.2 Arhitectura unui bloc de functii

Macrocelula unui CoolRunner II este extrem de eficienta si profilata pe creatia logica. Functiile uilizate sunt combinationale sau registrii. Schema unei astfle de macrocelule este prezentata in figura de mai jos:

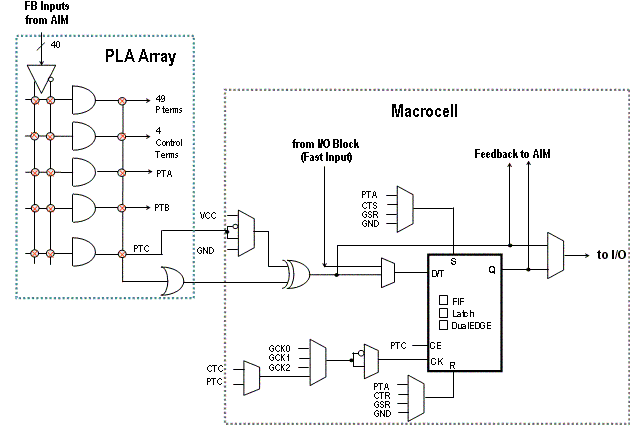
Figura 1.4.2.1.3 Arhitectura unei macrocelule

Blocurile I/O (blocurile de intrare/iesire) :fiecare intrare sau iesire poate functiona automat pt voltajul necesar sau poate fi programata sa functioneze pe acel domeniu.in figura 1.3.3.5 este prezentata arhitectura blocului de intrare/ iesire.

Clock division a fost introdus in arhitectura CoolRunner II CPLD pentru a divide un ceas global extern. Dividerile care sunt posibile sunt cu 2,4,6,8,10,12,14 si 16. aceasta posibilitate de dividere se poate implementa cu ajutorul unui pin:GCK2. in figura 1.3.3.4 este prezentata stuctura unui astfel de ceas.

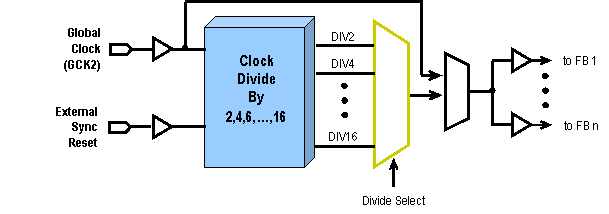
Figura 1.4.2.1.4 Structura Clock Division

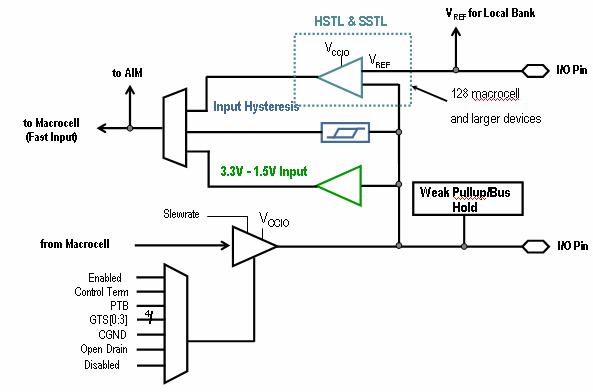
Figura 1.4.2.1.5 Arhitectura blocului de Intrare/Iesire

In figura de mai jos este prezentata structura unui XC2C256-TQ144 CoolRunner 2 acest circuit are urmatoarele caracteristici: dimensiunea este de 20mm x 20mm, distanta intre pini este de 0.5 mm iar numarul de intrari/iesiri este 118.

Figura 1.4.2.1.6 Structura unui XC2C256 -TQ144 CoolRunner 2