Sortarea prin interclasare directa cu doua cai

Interclasarea a doua siruri sortate.

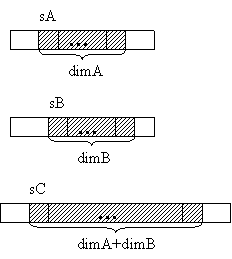
Se dau doua siruri ordonate crescator A[1..dimA] si B[1..dimB]. Ne punem problema sa construim sirul C[1..dimA + dimB] ordonat crescator ce contine toate elementele lui A si B. Este un prim exemplu de operatie de combinare a doua structuri: din doua structuri de acelasi tip (in cazul acesta structuri liniare si ordonate) producem o alta de acelasi tip, care este 'reuniunea' elementelor lor.

Algoritmul de interclasare are urmatoarea structura simpla:

Se parcurg simultan sirurile A, B si C. La fiecare pas se compara cele doua componente curente din A si B, iar cea mai mica dintre ele este mutata in C. Cand s-a terminat una din surse, A sau B, componentele ramase se adauga la C (ce poarta denumirea de destinatie). Procedura Merging ce-l implementeaza este data in continuare:

procedure Merging(dimA, dimB, A, B, C)

iA := 1; iB := 1; iC := 1;

while (iA £ dimA) and (iB £ dimB) do

if A[iA] < B[iB] then

C[iC = A[iA]

iA := iA + 1

else C[iC] := B[iB]

iB := iB + 1

endif

iC := iC + 1

endwhile

if iA > dimA then

for k := 0 to dimB - iB do C[iC + k] := B[iB + k]

else

for k := 0 to dimA - iA do C[iC + k]:=A[iA + k]

endif

endproc

Complexitatea algoritmului de interclasare: timp si spatiu.

Estimam complexitatea intai in functie de numarul de comparatii. La fiecare comparatie se muta in C o valoare, care nu va mai fi examinata ulterior de algoritm. Pentru a completa toate cele dimA + dimB locatii ale destinatiei C, vom face deci cel mult dimA + dimB - 1 comparatii (ultima componenta se muta in C fara a mai fi comparata).

In felul acesta, numarul maxim de comparatii pe care il face algoritmul de interclasare este C_max = dimA + dimB - 1. Este cazul cel mai nefavorabil, care se atinge daca ultimele componente ale surselor trebuie sa fie comparate intre ele, deci daca A[dimA] si B[dimB] vor fi cele mai mari elemente din C.

Exista si cazul cel mai favorabil, cu numar minim de comparatii C_min = min(dimA, dimB), caz care se atinge cand vectorul sursa de dimensiune mai mica are toate componentele mai mici decat cele din a doua sursa. Daca de exemplu dimB £ dimA si B[dimB] £ A[1], atunci se fac doar dimB comparatii, (dimB = min(dimA, dimB)), iar toate componentele din A se muta in C fara comparatii.

In ceea ce priveste numarul de mutari, el este tot timpul constant si egal cu M = dimA + dimB.

O caracteristica importanta a acestui algoritm, care-l plaseaza intr-o clasa distincta fata de toti ceilalti algoritmi discutati in acest capitol este faptul ca are nevoie de spatiu in plus, C[1..dimA + dimB], egal ca dimensiune cu spatiul necesar datelor de intrare. Cu alte cuvinte, fata de ceilalti algoritmi, spatiul utilizat este dublu.

Algoritmul se poate imbunatati ca sa foloseasca doar min(dimA, dimB) locatii in plus. Presupunem dimA = n, dimB = m si n³m. Alocam pentru A un numar de n + m locatii, sursa din A ordonata crescator de la A[n] la A[1], si punem rezultatul interclasarii in capatul liber al lui A (deoarece A are loc pentru cele m componente ale lui B). La mutari de elemente din A, se mai elibereaza locatii. Destinatia este A, ordonata de la A[n+m] la A[1].

Sortarea prin interclasare.

Putem folosi interclasarea pentru a sorta un vector. Algoritmul are urmatoarea structura:

(1) Se pleaca cu subvectori de lungime 1 ai lui A (care sunt sortati). Interclasand cate doi asemenea subvectori obtinem A impartit in subvectori de lungime 2 ordonati crescator.

(2) A este impartit in subvectori de lungime l ordonati crescator. Se interclaseaza cate doi, obtinand subvectori de lungime 2*l ordonati crescator (aceasta operatie se numeste pasa si este implementata de procedura MergePass.). Se reia pasul (2) pana cand avem un singur subvector.

Algoritmul este implementat de procedura MergeSort prezentata in continuare. Ea gestioneaza ca spatiu doi vectori A si B de aceeasi lungime, dimA, in modul urmator: la pasul (1) A este sursa iar B destinatie pentru interclasare. La pasul urmator, B este sursa si A destinatie s.a.m.d.

procedure Merge (dimA, dimB, dimC, sA, sB, sC, A, B, C)

.

begin

iA : = sA - 1;

iB : = sB - 1;

iC : = sC - 1;

while (iA < dimA + sA -1) and ( iB < dimB + sB - 1) do

begin

iC : = iC + 1;

if A[iA + 1] < B[iB + 1] then

begin

iA : = iA + 1;

C[iC = A[iA];

end

else

begin

iB : = iB + 1;

C[iC = B[iB]

end

end;

if iA > dimA + sA - 1 then

for k : = 1 to dimB + sB - iB - 1 do

C [iC + k] : = B[iB + k]

else

for k : =1 to dimA + sA - iA - 1 do

C[iC + k = A[iA + k]

end;

procedure MergePass ( n, l, A, B);

begin

q : = n / (l shl 1);

s : = ( l * q ) shl 1;

r : = n - s;

for i : = 1 to q do

begin

sA : = ((i - 1) * l) shl1 + 1;

Merge (l, l, sA, sA + l, sA , A, A, B)

end;

if r <= l then

for i : =1 to r do

B[s + i = A [s + i]

else

Merge (l, r - l, s + 1, s + l + 1, s + 1, A, A, B )

end;

procedure MergeSort (dimA, A);

begin

l : =1;

while l < dimA do

begin

MergePass(dimA, l, A, B);

MergePass(dimA, l * 2, B, A);

l : = l * 4

end;

end;

Complexitatea sortarii prin interclasare.

Daca la sortarea unui vector cu n componente facem k pasi iterativi pana ajungem sa-l sortam in intregime, inseamna ca intre k si n avem relatia 2^k-1 < n £ 2^k , de unde rezulta k = [log₂n]. Deoarece la un pas iterativ (care consta din cate o pasa pe subvectorii surse) facem aproximativ n/2 comparatii, rezulta ca algoritmul intra in clasa de complexitate O(n log₂n). Sa nu uitam insa ca el dubleaza dimensiunea spatiului de intrare.