Un vocabular al teoriei grafurilor

Definitia unui graf

Un graf este o pereche G = (V(G),E(G)), unde V(G) este o multime finita nevida, iar E(G) este o submultime a multimii P₂(V(G)) a partilor cu doua elemente ale lui V(G).

V(G) se numeste multimea varfurilor grafului G si numarul sau de elemente, |V(G)|, este ordinul grafului G; E(G) este multimea muchiilor grafului G si numarul sau de elemente, |E(G)|, este dimensiunea grafului G. Atunci cand nu exista posibilitatea confuziilor, vom nota simplu, G = (V, E).

Daca e = I E(G) este o muchie a grafului G vom nota e = uv (pentru simplificarea scrierii) si vom spune ca: muchia e uneste varfurile u si v; varfurile u si v sunt adiacente in G; muchia e este incidenta cu varfurile u si v; varfurile u si v sunt vecine in G; varfurile u si v sunt extremitatile muchiei e.

Daca v I V(G), atunci multimea N_G(v) = se numeste vecinatatea varfului v in G. Vom mai nota N_G(v) = G_G(v). Remarcam faptul ca graful G poate fi definit (in mod echivalent) ca o pereche (V(G), G_G) unde

G_G : V(G) P(V(G))

asociaza fiecarui varf vecinatatea sa ( astfel incat v h G_G(v) si daca w i G_G(v), atunci

v i G_G(w), pentru orice varfuri v si w ).

Doua muchii e si e' care au o extremitate comuna se numesc adiacente.

O multime independenta de varfuri sau multime stabila in G este o multime S V(G) de varfuri cu proprietatea ca P₂(S) E(G) = Æ (adica o multime de varfuri neadiacente doua cate doua). Cardinalul maxim al unei multimi stabile se numeste numarul de stabilitate sau numarul de independenta al grafului G si se noteaza cu a(G).

O multime independenta de muchii sau cuplaj in graful G este o multime de muchii neadiacente doua cate doua. Cardinalul maxim al unei multimi independente de muchii in G se numeste numarul de muchie-independenta al grafului G si se noteaza n(G).

Intuitiv, un graf G = (V(G), E(G)) poate fi reprezentat (dupa cum sugereaza si numele sau) cu ajutorul unei figuri plane formata dintr-o multime de cerculete ingrosate aflata in corespondenta cu multimea de varfuri V(G), doua cerculete fiind unite printr-o curba simpla daca si numai daca, perechea de varfuri corespunzatoare lor este o muchie a grafului G.

De exemplu, graful G = (V, E) unde V = si E = poate fi reprezentat de

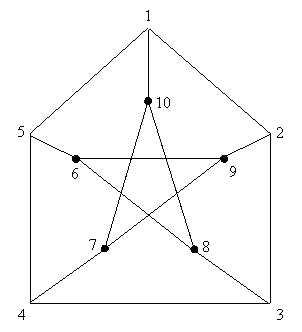
Sa observam ca in acest graf:

Multimea de varfuri este stabila si este de cardinal maxim, deci a(G) = 4; multimea de muchii formeaza un cuplaj de cardinal maxim, deci n(G) = 5.

Daca G = (V(G), E(G)) este un graf si p I N^*, se numeste p-colorare a (varfurilor) lui G o aplicatie c : V(G) cu proprietatea ca c^-1(i) este o multime stabila in G, ( ) i I (remarcam ca, din definitia multimilor stabile, Æ este o multime stabila). Numarul cromatic al grafului G, notat c(G), este cea mai mica valoare a lui p I N^* pentru care G admite o p-colorare.

O p-colorare a muchiilor lui G este o aplicatie c : E(G) cu proprietatea ca c^-1(i) este un cuplaj al lui G, ( ) i I . Indicele cromatic al grafului G, notat c'(G), este cea mai mica valoare a lui p I N^* pentru care G admite o p-colorare a muchiilor.

Doua grafuri, G = (V(G), E(G)) si H = (V(H), E(H)) se numesc izomorfe, si notam aceasta prin G H, daca exista o bijectie j : V(G) V(H) cu proprietatea ca aplicatia y : E(G) E(H), definita pentru orice uv I E(G) prin y(uv) = j(u)j(v), este o bijectie (deci, doua grafuri sunt izomorfe daca exista o bijectie intre multimile lor de varfuri care induce o bijectie intre multimile lor de muchii).

Variatii in definitia unui graf

a)              Daca in definitia unui graf, se considera E(G) o multimultime pe P₂(V(G)), adica este data o functie

m : P₂(V(G)) N,

se obtine notiunea de multigraf. Un element e I P₂(V(G)) cu m(e) > 0 este muchie a multigrafului, simpla daca m(e) = 1, multipla daca m(e) > 1. Oricarui multigraf M i se poate asocia un graf G(M), numit graful suport al lui M, obtinut prin inlocuirea fiecarei muchii multiple cu o singura muchie cu aceleasi extremitati.

b)              Daca in definitia unui graf se considera E(G) ca o multimultime pe multimea partilor nevide cu cel mult doua elemente ale lui V(G), atunci G se numeste graf general sau pseudograf. O muchie e I E(G), e = se numeste bucla in varful v. Pictural pseudografurile se reprezinta la fel ca si grafurile.

Pentru evitarea confuziilor, uneori grafurile - asa cum le-am definit - se mai numesc si grafuri simple.

c)              Un digraf este o pereche D = (V(D), A(D)) unde V(D) este o multime finita nevida (multimea varfurilor digrafului D), iar A(D) V(D) V(D) este multimea arcelor digrafului D. Daca a = (u, v) este arc in D, notam a = uv si spunem ca u si v sunt adiacente; a este incident din u; a este incident spre v; u domina pe v; a este incident cu u spre exterior ; a este incident cu v spre interior ; u este extremitatea initiala a lui a si v este extremitatea finala a lui a.

Pictural, digrafurile se reprezinta la fel ca si grafurile, adaugand curbei care uneste doua cerculete un sens pentru a preciza perechea de varfuri corespunzatoare arcului desenat.

O pereche de arce de forma vw si wv se numeste pereche simetrica de arce. Daca D este un digraf, inversul sau D' este digraful obtinut din D prin inlocuirea fiecarui arc vw cu opusul sau wv.

Daca D este un digraf, atunci inlocuind fiecare arc cu multimea de varfuri care il formeaza, obtinem, in general, un multigraf M(D). Graful suport al acestui multigraf se numeste graful suport al grafului D. Daca M(D) este graf atunci D se numeste graf orientat (poate fi gandit ca obtinut prin "orientarea" fiecarei muchii a grafului M(D)).

Un digraf complet simetric este un digraf in care fiecare pereche de varfuri este unita prin exact o pereche de arce simetrice. Un turneu este un digraf in care orice doua varfuri sunt unite prin exact un arc.

d)              Grafurile infinite se obtin prin inlaturarea conditiei de finitudine a multimii de varfuri si (sau) muchii. Un graf G local finit este un graf finit in care N_G(v) este finita pentru orice varf v.

Grade

Daca G = (V, E) este un graf si v I V un varf al sau, atunci valenta sau gradul lui v in G, notat d_G(v) sau p_G(v), este

||.

Un varf de grad 0 se numeste izolat; un varf de grad 1 se numeste pendant. Daca toate varfurile lui G au aceeasi valenta p atunci G se numeste graf p - valent sau p - regulat. Un graf 0 - valent se numeste graf nul. Un graf 3 - valent se numeste graf trivalent sau cubic. Un exemplu de graf trivalent este graful lui Petersen:

Concepte analoage se pot defini si pentru digrafuri. Daca v este un varf al digrafului D atunci valenta interioara sau gradul interior notat p_in(v) sau sau , este numarul arcelor incidente cu v spre interior; valenta extrerioara sau gradul exterior notat p_out(v) sau

sau , este numarul arcelor incidente cu v spre exterior.

Subgrafuri

Un subgraf al grafului G = (V(G), E(G)) este un graf H = (V(H), E(H)) care satisface: V(H) V(G) si E(H) E(G).

Daca V(H) = V(G) atunci H se numeste graf partial al lui G.

A V(G) atunci [A]_G = (A, P₂(A) E(G)) se numeste subgraf indus in G de multimea de varfuri A. subgraful [V(G) A]_G se noteaza G - A si este subgraful lui G obtinut prin indepartarea varfurilor din A; in particular, daca A = , atunci G - se noteaza G - v.

Daca E' E(G) atunci E'ñ_G = (V(G), E') este graful partial sectionat de E' in G. G - E' este prin definitie E(G) E'ñ_G, iar G - e = G - (e I E(G)).

Concepte similare se pot defini in mod analog pentru multigrafuri, grafuri generale sau digrafuri.

Operatii cu grafuri

Daca G = (V(G), E(G)) este un graf, atunci:

complementarul sau este graful cu V() = V(G) si

E() = P₂(V(G)) E(G).

graful reprezentativ al muchiilor lui G este graful L(G) cu V(L(G)) = E(G) si E(L(G)) = .

graful total al grafului G este graful T(G) cu V(T(G)) = V(G) È E(G) si E(T(G)) = .

graful obtinut din G prin insertia unui varf (z) pe o muchie (e = vw) este graful G' = (V(G) È , E(G) È ) (z Ï V(G), e I E(G)). Doua grafuri obtinute prin insertii succesive de varfuri pe muchiile aceluiasi graf se numesc homeomorfe.

graful obtinut din G prin contractia muchiei e = vw I E(G) este graful G | e = (V(G) È , E([V(G) ]_G) È). Daca H se poate obtine prin contractii succesive de muchii din graful G, se spune ca G este contractibil la H.

Fie G = (V(G), E(G)) si G' = (V(G'), E(G')) doua grafuri.

Daca V(G) = V(G') atunci reuniunea celor doua grafuri si intersectia lor se definesc G È G' = .

Clase de grafuri

Graful complet de ordin n: K_n cu |V(K_n)| = n si E(K_n) = P₂(V(K_n)).

Graful nul de ordin n: N_n = .

Circuitul de ordin n: C_n cu V(C_n) = si E(C_n) = .

Drumul de ordin n: P_n = C_n - e (e I E(C_n)).

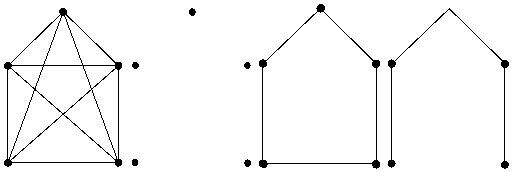
Exemplu (n = 5)

K₅ N₅ C₅ P₅

Un subgraf complet al unui graf G se numeste clica a lui G. Cardinalul maxim al unei clici a lui G se numeste numarul de clica sau numarul de densitate al lui G si se noteaza w(G) (evident w(G) = a()).

Un graf bipartit este un graf G cu proprietatea ca V(G) se poate partitiona in doua multimi independente in G. Daca S si T satisfac S È T = V(G), S È T = Æ si S, T sunt independente si nevide in G, atunci graful bipartit G se noteaza G = (S, T; E(G)). Remarcam ca ( ) e I E(G) are o extremitate in S si cealalta in T. Daca ( ) v I S si ( ) w I T vw I E(G), atunci graful bipartit G = (S, T; E(G)) se numeste graf bipartit complet si se noteaza K_s,t unde s = |S| si t = |T|. Exemplu: K_3,3 este graful

Un graf G = (V(G), E(G)) se numeste planar daca poate fi scufundat in plan astfel incat fiecarui varf sa-i corespunda un punct al planului, iar muchiilor le corespund curbe simple ce unesc punctele corespunzatoare varfurilor lor si in plus aceste curbe se intersecteaza (eventual) numai in varfuri. Un graf care nu-i planar se numeste neplanar. Exemple minimale de grafuri neplanare sunt grafurile K₅ si K_3,3.

Drumuri si circuite

Fie G = (V(G), E(G)) un graf. Se numeste mers de lungime r de la v la w in G un sir de varfuri si muchii

(v =) v₀,v₀v₁, . . ., v_{r - 1}, v_{r - 1}v_r, v_r (= w)

v si w se numesc extremitatile mersului.

Daca muchiile mersului sunt distincte atunci mersul se numeste parcurs in G de la v la w. Daca varfurile sunt distincte atunci mersul se numeste drum de la v la w.

Daca v = w atunci mersul (parcursul) se numeste inchis; daca intr-un mers toate varfurile sunt distincte, cu exceptia extremitatilor, atunci mersul se numeste circuit (sau drum inchis). Un circuit este par sau impar dupa cum lungimea sa (numarul muchiilor) este para sau impara. Lungimea celui mai scurt circuit al grafului G (daca G are circuite) se numeste gratia grafului G si se noteaza cu g(G); lungimea celui mai lung circuit al lui G se numeste circumferinta lui G si se noteaza c(G).

Daca v si w sunt varfuri ale lui G, lungimea celui mai scurt drum de la v la w in G se numeste distanta in G de la v la w si se noteaza d_G(v, w). Diametrul grafului G, notat d(G) este d(G) = max .

Definitiile de mai sus se extind, in mod evident, pentru digrafuri singura modificare fiind aceea ca se inlocuiesc muchiile cu arce.

Un graf este conex daca exista un drum intre orice doua varfuri ale sale; un graf care nu este conex se numeste neconex. Orice graf G poate fi unic exprimat ca o reuniune disjuncta de subgrafuri induse conexe si maximale cu aceasta proprietate; aceste subgrafuri se numesc componentele conexe ale grafului G (mai precis, se pot defini componentele conexe ca subgrafurile induse de clasele de echivalenta determinate pe V(G') de relatia de echivalenta r definita prin vrw daca exista in G un drum de la v la w).

Concepte analoage se pot defini si pentru digrafuri; daca D este un digraf atunci:

D este tare conex daca (v, w) I V(D) V(D) exista un drum in D de la v la w;

D este unilateral conex daca (v, w) I V(D) V(D) exista in D un drum de la v la w sau de la w la v;

D este conex daca G(D), graful suport al lui D, este conex.

Un graf conex care nu are circuite se numeste arbore. Un graf ale carui componente conexe sunt arbori se numeste padure.

Daca G este un graf conex, un varf v I V(G) cu proprietatea ca G - v este neconex se numeste varf (punct) de articulatie; mai general, o multime A de varfuri ale unui graf G se mai numeste multime separatoare de varfuri (multime de articulatie) daca G - A este neconex. Fie p un numar intreg pozitiv; un graf G cu macar p varfuri este p - conex daca G = K_p sau are cel putin p + 1 varfuri si nu admite multimi separatoare de varfuri de cardinal mai mic decat p. Evident, G este 1 - conex daca si numai daca este conex. Un graf 2 - conex se numeste bloc.

Daca G este un graf conex, o muchie e I E(G) cu proprietatea ca G - e este neconex se numeste punte in graful G; mai general, o multime A de muchii ale unui graf G se numeste multime separatoare de muchii daca G - A este neconex. Un graf G cu macar p varfuri este p - muchie - conex daca nu admite multimi separatoare de muchii de cardinal mai mic decat p.

Numarul de conexiune al lui G, notat k(G), (respectiv, numarul de muchie - conexiune, l(G)) este cel mai mare numar natural p pentru care G este p - conex (p - muchie - conex).

Un graf (sau digraf) se numeste eulerian daca admite un parcurs inchis care foloseste fiecare muchie a grafului (respectiv, fiecare arc al digrafului).

Un (di)graf G se numeste hamiltonian daca are un circuit care trece prin fiecare varf.

Matrici asociate.

Daca G = (, ) este un graf, atunci matricea de adiacenta a grafului G este matricea A = (a_ij)_{n n}, unde

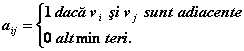
Matricea de incidenta a grafului G este matricea B = (b_ij)_{n m}, unde

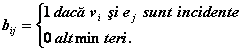
In cazul digrafurilor, se pot asocia similar astfel de matrici, in care, evident se poate indica si orientarea arcelor, folosind elementele 0, 1 si -1.

Valorile proprii si polinomul caracteristic ale matricii de adiacenta se numesc valorile proprii ale grafului, respectiv, polinomul caracteristic al grafului.

Structuri de date utilizate in reprezentarea (di)grafurilor.

Fie G = (V, E) un (di)graf cu V = si |E| = e. Cele mai uzuale structuri de date utilizate pentru reprezentarea (di)grafului G sunt

a)              matricea de adiacenta

Daca A = (a_ij)_{n n} este matricea de adiacenta a lui G (a_ij := 1 if ij I E este 0) atunci, reprezentarea acesteia cu ajutorul unui tablou bidimensional va necesita O(n²) operatii pentru orice initializare, deci orice algoritm, care foloseste o astfel de reprezentare, are complexitatea W(n²).

b)              listele de adiacenta

Pentru fiecare varf v I V se considera o lista A(v) a vecinilor sai in G. Daca G este graf, atunci A(v) contine N_G(v) = iar daca G este digraf atunci A(v) contine (v) = . Pentru cazul in care G este graf, fiecare muchie vw I E va genera doua elemente in listele de adiacenta, unul in A(v) si celalalt in A(w). Spatiul total de memorie utilizat va fi de O(n + 2e). Pentru cazul in care G este digraf, spatiul de memorie utilizat este de O(n + e). Listele de adiacenta pot fi reprezentate b1) cu ajutorul tablourilor si b2) ca structuri dinamice de date.

b1) Se va considera tabloul T : array [1 . . p, 1 . . 2] of integer unde p = n + 2e daca G este graf si p = n + e daca G este digraf. Vom initializa T(i, 1) := i i = ; T(i, 2) := adresa in T (indicele) primului element din A(i). Daca i I V este varf izolat, atunci T(i, 2) = 0. Daca T(i, 2) = j atunci T(j, 1) este primul varf din A(i) iar T(j, 2) este adresa urmatorului element. Daca l este adresa ultimului element w din A(i), atunci T(l, 1) = w si T(l, 2) = 0.

b2) Se folosesc urmatoarele declaratii:

type pointer = ^elem;

elem = record

varf : 1 . . n;

leg : pointer;

end;

si un tablou care contine trimiteri la inceputul fiecarei liste:

var cap : array [1 . . n] of pointer;

p : pointer;

Graful nul de ordin n se initializeaza astfel:

for i := 1 to n do cap[i] := nil;

Adaugarea muchiei ij (deci in cazul grafurilor):

begin

new(p);

p^.varf := j;

p^.leg := cap[i];

cap[i] := p;

new(p);

p^.varf := i;

p^.leg := cap[j];

cap[j] := p;

end;

Notam ca in descrierea data am reprezentat listele A(i) ca stive cu elementele din top la adresa cap[i] (i I V). Aceste liste se pot organiza si sub forma unor cozi sau liste dublu inlantuite, sau chiar liste circulare, in functie de problema care se rezolva pe (di)graful in cauza.

Sortare topologica. Dat G = (V, E) un digraf, sa se determine o numerotare aciclica a varfurilor sale.

Vom presupune ca V = , si ca digraful este reprezentat prin listele sale de adiacenta A(v), deci cu ajutorul tabloului cap[v] v I V.

Problema cere sa determinam vectorul ord[v] v I V, (ord[v] = numarul de ordine al varfului v) astfel incat

vw I E Þ ord[v] < ord[w].

Vom transforma si listele de adiacenta astfel incat ele sa fie ordonate crescator (in noua numerotare). Rezolvarea problemei este simpla si se bazeaza pe urmatoarea

Lema. G admite o numerotare aciclica daca si numai daca nu are circuite.

Demonstratie. Este evident ca daca G admite o numerotare aciclica atunci G nu are circuite (daca vv₁, v₂, . . ., v_k, v₁ sunt varfurile unui circuit atunci, cum G are o numerotare aciclica, obtinem ord[v₁] < ord[v₂] < . . . < ord[v_k] < ord[v₁], contradictie).

Reciproc, daca G nu are circuite atunci exista un varf v₀ I V astfel incat (v₀) = 0 (astfel, datorita finitudinii digrafului, se poate construi un circuit); punem ord[v₀]:= 1, consideram G := G - v₀ si repetam rationamentul.

Dimensiunea problemei este O(n + e). Vom construi un algoritm care sa rezolve problema in timp O(n + e). Acest lucru este posibil datorita unei utilizari judicioase a structurilor de date. Idea algoritmului:

determinam gradele interioare ale varfurilor;

varfurile de grad interior 0 le memoram intr-o stiva S₀;

(a)    - consideram varful din topul stivei S₀ si-l numerotam;

(b)   - modificam gradele interioare ale varfurilor din lista de adiacenta a varfului tocmai numerotat;

(c)    - in modificarea anterioara crearea unui varf de grad interior 0 va implica memorarea lui in stiva S₀;

(d)   - reluam secventa (a) - (c) pana cand stiva devine vida.

Daca nu s-au numerotat toate varfurile rezulta ca digraful contine circuite; in cazul epuizarii varfurilor, s-a rezolvat prima parte a problemei. Va trebui sa sortam listele (stivele) de adiacenta asa incat ele sa fie ordonate crescator in noua numerotare. Vom folosi un caz foarte simplu al sortarii cu galeti (bucket - sort) sau hash - sort:

colectam in galeata k I toate varfurile j cu proprietatea ca jk I E (j si k sunt noua numerotare).

parcurgem galetile de la cea mai mare la cea mai mica (n 1) si golim galeata curenta i astfel: adaugam i la stiva vecinilor fiecarui varf j "cules" din galeata i.

Dupa terminarea acestui pas, in stiva vecinilor fiecarui varf vom avea varfurile sortate crescator in noua numerotare. Pentru a se putea folosi noua reprezentare a digrafului va trebui, desigur inversata permutarea ord.

Descrierea algoritmului:

type pointer = ^elem;

elem = record

varf: 1 . . n;

prec: pointer;

end;

var cap : array [1 . . n] of pointer;

gal : array [1 . . n] of pointer;

top0 : pointer;

p1, p : pointer;

v, i, j, nr : integer;

d : array [1 . . n] of integer;

ord : array [1 . . n] of integer;

begin

nr := 0;

top0 := nil;

for i := 1 to n do

begin

p := cap[i];

while p <> nil do

begin

j := p^.varf;

d[j] := d[j] + 1;

p := p^.prec

end

end;

for i := 1 to n do

if d[i] = 0 then

begin

new(p);

p^.varf := i;

p^.prec := top0;

top0 := p;

end;

while top0 <> nil do

begin

v := top0^.varf;

top0 := top0^.prec;

nr := nr + 1;

ord[v] := nr;

p := cap[v];

while p <> nil do

begin

j := p^.varf;

d[j] := d[j] - 1;

if d[j] = 0 then

begin

new(p1);

p1^.varf := j;

p1^.prec := top0;

top0 := p1;

end;

p := p^.prec;

end;

end;

if nr < n then

write ("digraful are circuite")

else

begin

for i := 1 to n do

gal[i] := nil;

for i := 1 to n do

begin

p := cap[i];

j := ord[i];

while p <> nil do

begin

k := ord(p^.varf);

new(p1);

p1^.varf := j;

p1^.prec := gal[k];

gal[k] := p1;

p := p^.prec;

end;

end;

for i := 1 to n do

cap[i] := nil;

for i := n downto 1 do

begin

p := gal[i];

while p <> nil do

begin

k := p^.varf;

new(p1);

p1^.varf := i;

p1^.prec := cap[k];

cap[k] := p1;

p := p^.prec;

end;

end;

end;

end.

Descrierea acestui algoritm este tipica pentru anumite libertati Pascal pe care le vom folosi peste tot in cele ce urmeaza in scopul maririi lizibilitatii textului.