Modelul relational al datelor

Prezentare generala

Modelul relational a fost conceput si dezvoltat de E. F. Codd, fiind un model formal de organizare conceptuala a datelor, destinat reprezentarii datelor si legaturilor dintre date, bazat pe teoria matematica a relatiilor.

Datele se prezinta sub forma unor tabele (relatii) in care liniile constituie inregistrari, iar coloanele sunt atribute ce caracterizeaza aceste inregistrari. Orice interogare (sau consultare, extragere de date) este tot o relatie.

Din punctul de vedere al manipularii datelor, modelul relational este orientat spre multimi. Modelul relational nu este orientat spre sistemul de calcul, deci nu include regulile, structurile si operatiile referitoare la implementarea fizica a unui sistem de baze de date.

Modelul relational a permis introducerea unui limbaj de interogare, neprocedural de manipulare a datelor.

Un model relational se caracterizeaza prin trei elemente:

Structura relationala a datelor

Operatorii modelului relational

Regulile de integritate care guverneaza folosirea cheilor in model.

Aceste trei elemente corespund celor trei componente ale ingineriei software: informatie, proces si integritate.

Organizarea datelor

Structura datelor impune definirea notiunilor: relatie, schema relationala, valoare nll, tabel vizualizare (view), care pot fi exprimate formal, uzual sau fizic (tabelul 1):

Un domeniu este o multime de valori care poate fi definita fie enumerand elementele componente, fie definind o proprietate distinctiva a domeniului valorilor.

Fie D₁, D₂, ., D_n domenii finite, nu neaparat disjuncte. Atunci produsul cartezian D₁ X D₂ X .X D_n este definit de multimea tuplurilor (v₁, v₂, ., v_n), unde v₁ D₁, v₂ D₂, ., v_n D_n, unde n este aritatea tuplului:

D₁ X D₂ X .X D_n =

O relatie R pe multimile D₁, D₂, ., D_n este o submultime a produsului cartezian D₁ X D₂ X .X D_n, deci este o multime de tupluri.

O relatie poate fi considerata o multime finita de functii.

Atribut: Asociem fiecarui domeniu D_i un atribut A_i si definim relatia R = unde f_i : D₁ X D₂ X .X D_n si f_i (A_j) D_j, i,j.

Schema relationala: Multimea numelor atributelor corespunzatoare unei relatii R defineste schema relationala a relatiei respective si se noteaza R(A₁, A₂, ., A_n).

Se poate reprezenta o relatie printr-un tabel bidimensional in care fiecare linie corespunde unui tuplu si fiecare coloana corespunde unui domeniu din produsul cartezian. O coloana ii corespunde unui atribut. Numarul atributelor defineste gradul relatiei, iar numarul de tupluri din relatie defineste cardinalitatea relatiei.

O valoare null este un atribut necunoscut sau care nu poate fi definit.

Un tabel vizualizare ( view, filtru, relatie virtuala, vedere) este un filtru asupra tabelului initial care contine numai informatia necesara unei anumite abordari sau aplicatii. O vedere este virtuala deoarece datele continute nu sunt in realitate memorate intr-o baza de date. Exista limitari in folosirea acestor tabele: de exemplu, nu se recomanda inserarea, reactualizarea si stergerea.

Reguli de integritate

Regulile de integritate sunt asertiuni pe care datele din baza de date trebuie sa le satisfaca. Exista trei tipuri de constrangeri structurale:

de cheie

de referinta

de entitate

care constituie multimea minimala de reguli de integritate pe care trebuie sa le respecte un sistem de gestiune a bazelor de date relationale.

Restrictiile de integritate minimale sunt definite in raport cu notiunea de cheie a unei relatii.

O cheie a unei relatii R este o multime k de atribute astfel incat:

pentru orice doua tupluri t₁, t₂ ale lui R, sa avem t₁(k) # t₂(k)

nu exista nici o submultime proprie a lui k avand proprietatea 1.

Fiecare relatie are cel putin o cheie. Daca exista mai multe chei, exista o cheie primara.

Cheie externa (straina): Fie schemele relationale R₁(P₁, S₁) si R₂(S₁, S₂), unde P₁ este cheie primara in R₁ si S₁ - cheie secundara in R₁, S₁ - cheie primara in R₂. Atunci S₁ este cheie externa pentru R₁.

Reguli de integritate structurata: Modelul relational respecta 3 reguli de integritate structurata:

Regula 1: unicitatea cheii - Cheia primara trebuie sa fie unica si minimala.

Regula 2 integritatea entitatii - Atributele cheii primare trebuie sa fie diferite de valoarea null.

Regula 3: integritatea referirii - O cheie externa trebuie sa fie ori null in intregime, ori sa corespunda unei valori a cheii primare asociate.

Proiectarea modelului relational

Diagrama E/R (entitate-relatie) este un model neformalizat pentru reprezentarea grafica a structurii relationale.

Modelul E/R imparte elementele unui sistem real in doua categorii:

entitati si

relatii (legaturi, asocieri) intre aceste enti tati.

O entitate poate fi o persoana, un loc, concept, activitate, eveniment care este semnificativ pentru modelare.

O relatie (asociere) este o comunicare intre doua sau mai multe entitati, un raport intre entitati.

Pentru obtinerea schemei conceptuale a bazei de date relationale, se pleaca de la modelele conceptuale ale datelor (diagrama E/R).

Exemplu: Fie o institutie ce contine mai multe departamente, in care lucreaza salariati. Salariatii sunt atasati unor proiecte, executand in cadrul acestora diferite sarcini.

Structura generala a modelului analizat este prezentata in figura 1.:

Se pot defini urmatoarele:

Entitati - SALARIAT, DEPARTAMENTE, PROIECT, SARCINA

Observatii:

Entitatile devin tabele in modelele relationale.

Cheia primara identifica unic o entitate si face distinctie intre valori diferite ale entitatii.   

Relatii - in modelul relational, devin tabele speciale sau coloane speciale care refera chei primare (inscris_la, lucreaza_in, conduce, apartine)

Atribut - o proprietate descriptiva a unei entitati / relatii

Proiectarea diagramei entitate-relatie (E/R)

Se folosesc urmatoarele reguli:

Entitatile se reprezinta prin dreptunghiuri;

Relatiile se reprezinta prin arce neorientate;

Atributele ce sunt chei primare sunt specificate prin simbolul #

Cardinalitatea (numarul de tupluri ale relatiei): cardinalitatea minima foloseste simbolurile ,(, si ,)', iar cardinalitatea maxima se specifica fara paranteze.

Cazurile speciale luate in considerare:

O entitate dependenta: SARCINA depinde de PROIECT. Cheia primara a unei entitati dependente include cheia primara a sursei (nr._proiect).

Clasa este un grup de subentitati, clasificate dupa valorile unor atribute. Se aliniaza vertical.

Se pot defini relatii recursive. Exemplu: SALARIAT_supervizeaza_SALARIAT.

Diagrama E/R este prezentata in figura 2.:

Din diagrama E/R se obtine schema conceptuala a bazei de date relationale. Se reprezinta entitatile si legaturile dintre ele sub forma unor tabele speciale (relatii).

Regulile de conversie se bazeaza pe minimizarea numarului de valori null si a redundantei datelor, astfel:

a)      Transformarea entitatilor se bazeaza pe regulile:

Entitatile independente devin tabele independente. Cheia primara nu contine chei externe.

Exemplu: entitatea independenta SALARIAT genereaza un tabel independent pentru care atributul cod_salariat este cheia primara.

Entitatile dependente devin tabele dependente. Cheia primara a entitatilor dependente contine cheia primara a entitatii de care depinde plus unul sau mai multe atribute aditionale.

Exemplu: cheia primara a entitatii SARCINA este formata din nr._proiect (cheia primara a entitatii PROIECT) si nr._sarcina.

Subentitatile devin subtabele.

b)      Transformarea relatiilor foloseste regulile:

Relatiile 1:1 si 1:n devin chei externe. Astfel, relatia "conduce' devine coloana in tabelul DEPARTAMENTE si relatia ,lucreaza_in' este coloana in tabelul SALARIAT.

Simbolul "X" marcheaza plasamentul cheii externe.

Simbolul "X" - cheia externa este continuta de cheia primara.

Relatia m:n devine un tabel    special (tabel asociativ) care are 2 chei externe pentru cele 2 tabele asociate. Cheia primara este formata din compunerea celor 2 chei externe plus coloane aditionale. Se specifica punctat.

c)      Transformarea atributelor foloseste regulile:

Un atribut singular devine o coloana.

Atributele multiple devin tabele dependente ce contin cheia primara a entitatii si atributul multiplu.

Exemplu: un SALARIAT are mai multe numere de telefon nr._telefon este atribut multiplu care genereaza tabelul dependent TELEFON.

Concluzie din diagrama E/R se obtine diagrama conceptuala (figura 3.) pentru proiectarea modelului relational prin:

adaugarea tabelelor asociative

marcarea cheilor externe.

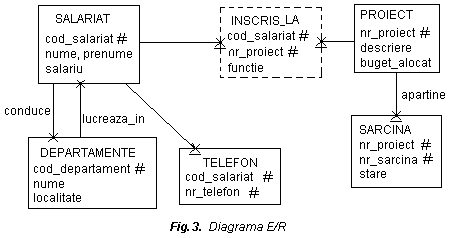
Schemele relationale obtinute sunt:

SALARIAT(cod_salariat#, nume, prenume, salariu, lucreaza_in)

DEPARTAMENTE(cod_departament#, nume, localitate, conduce)

INSCRIS_LA(cod_salariat#, nr._proiect#, functie)

PROIECT(nr._proiect#, descriere, buget_alocat)

SARCINA(nr._proiect#, nr._sarcina#, stare)

TELEFON(cod_salariat#, nr._telefon#)

Deci tipurile de tabele folosite in diagrama E/R pot fi:

independente

dependente

subtabele

tabele asociative

Semnificatia fiecarui tabel si relatia dintre cheie primara si cheie externa sunt prezentate in tabelul 2:

O relatie de tip 3 este o legatura intre 3 entitati: SALARIAT_asociat_la_PROIECT_in_FUNCTIA

Algebra relationala

A fost introdusa de E. F. Codd ca o multime de operatii formale actionand asupra unor relatii si avand ca rezultat alte relatii.

Baza teoretica fundamentala pentru limbajele de interogare relationale o constituie cei opt operatori introdusi de Codd pentru manipularea relatiilor.

Operatorii algebrei relationale

SELECT (operatorul selectie) extrage tupluri (linii) ce satisfac o conditie specificata, producand o submultime pe orizontala;

PROJECT (operatorul proiectie) extrage atributele specificate, producand o submultime pe verticala;

UNION (operatorul reuniune) reuneste doua relatii. Operatorul UNION elimina automat liniile identice din rezultat;

INTERSECT (operatorul intersectie) extrage tupluri care apar in ambele relatii; este operator binar comutativ:

DIFFERENCE (operatorul diferenta) extrage tupluri care apar intr-o relatie, dar nu apar in cealalta. Este operator binar necomutativ.

PRODUCT (operatorul produs cartezian) genereaza toate perechile posibile de tupluri, primul element al perechii fiind din prima relatie, al doilea element din a doua relatie, s.a.m.d.

Fie R, S relatii de aritate n, respectiv m. Produsul cartezian al lui R cu S este multimea tuplurilor de aritate n+m unde primele n componente formeaza un tuplu in R, iar ultimele m componente formeaza un tuplu in S.

DIVISION (operatorul diviziune) extrage valorile atributelor dintr-o relatie, care apar in toate valorile atributelor din cealalta relatie, fiind operator binar.

Fie doua relatii R⁽ⁿ⁾ si S^(m). Atunci DIVISION(R, S) (sau DIVIDE(R, S)) permite selectarea acelor tupluri de dimensiune n-m la care, adaugand orice tuplu din S, se obtine un tuplu din R.

Operatorul DIVISION este legat de cuantificatorul universal ,' care nu exista in limbajul SQL, dar poate fi simulat astfel: Fie un predicat P(x). Atunci are loc identitatea:   

JOIN (operatorul de compunere, de jonctiune) permite extragerea informatiilor din mai multe relatii corelate. Jonctiunea este o combinatie de produs cartezian si selectie.

Regulile lui Codd

In 1985, Codd a publicat un set de 13 reguli in raport cu care un SGBD poate fi apreciat ca relational:

Regula 1 - regula gestionarii datelor - Un SGBD relational trebuie sa fie capabil sa gestioneze o baza de date prin posibilitatile sale relationale.

Regula 2 - regula reprezentarii informatiei - Intr-o baza de date relationala, informatia este reprezentata la nivel logic sub forma unor tabele (relatii).

Regula 3 - regula accesului garantat la date - Fiecare valoare dintr-o baza de date relationala trebuie sa poata fi adresata in mod logic printr-o combinatie formata din numele relatiei, valoarea cheii primare si numele atributului.

Regula 4 - regula reprezentarii informatiei necunoscute - Un sistem relational trebuie sa permita utilizatorului definirea unui tip de date numit null pentru reprezentarea informatiei necunoscute la momentul respectiv.

Regula 5 - regula dictionarelor de date - Asupra descrierii bazei de date (informatii relative la relatii, vizualizari, indecsi) trebuie sa se poata aplica aceleasi operatii ca si asupra datelor din baza de date.

Regula 6 - regula limbajului de interogare - Trebuie sa existe cel putin un limbaj pentru manipularea bazei de date (limbajul SQL).

Regula 7 - regula de actualizare a vizualizarii - Un SGBD trebuie sa poata determina daca o vizualizare poate fi actualizata si sa stocheze rezultatul interogarii intr-un dictionar de tipul unui catalog de sistem.

Regula 8 - regula limbajului de nivel inalt - Regulile de manipulkare asupra unei relatii luata ca intreg sunt valabile atat pentru operatiile de regasire a datelor, cat si asupra operatiilor de inserare, actualizare si stergere a datelor.

Regula 9 - regula independentei fizice a datelor - Programele de aplicatie nu depind de modul de stocare a datelor sau de modul de acces la date.

Regula 10 - regula independentei logice a datelor - Programele de aplicatie trebuie sa fie transparente la modificarile de orice tip efectuate asupra datelor.

Regula 11 - regula independentei datelor din punct de vedere al integritatii - Regulile de integritate trebuie sa fie definite intr-un sublimbaj relational, nu in programul de aplicatie.

Regula 12 - regula independentei datelor din punct de vedere al distribuirii datelor - Distribuirea datelor pe mai multe calculatoare dintr-o retea de comunicatii de date, nu trebuie sa afecteze programele de aplicatie.

Regula 13 - regula versiunii procedurale a unui SGBD - Orice componenta procedurala a unui SGBD trebuie sa respecte aceleasi restrictii de integritate ca si componenta relationala.

Deoarece regulile lui Codd sunt prea restrictive pentru a fi respectate de un SGBD relational, s-au formulat criterii minimale de definire a unui sistem de gestiune relational.

Un SGBD este minimal relational daca:

toate datele bazei sunt reprezentate prin valori in tabele;

nu exista pointeri observabili de catre utilizator;

sistemul suporta operatorii relationali de proiectie, selectie si compunere naturala, fara limitari impuse din considerente interne.

Un SGBD este complet relational daca este minimal relational si satisface in plus conditiile:

sistemul suporta restrictiile de integritate de baza (unicitatea cheii primare, constrangerile referentiale, integritatea entitatii)

sistemul suporta toate operatiile de baza ale algebrei relationale.

Mecanismele de lucru de care dispune un SGBD relational sunt:

un limbaj relational pentru descrierea datelor la nivel fizic, logic si conceptual

un limbaj relational pentru manipularea datelor

mecanisme pentru controlul integritatii semantice a datelor

mecanisme pentru optimizarea cererilor de date

mecanisme pentru asigurarea coerentei datelor

utilitare pentru generarea de rapoarte, aplicatii sau statistici referitoare la starea si activitatea bazei de date.

Normalizarea relatiilor

Normalizarea relatiilor conceptuale permite obtinerea de relatii "moleculare", fara a pierde nimic din informatie, pentru a elimina redundanta si anomaliile reactualizarii informatiilor. Este un proces de ameliorare progresiva a unei scheme conceptuale initiale a bazei de date relationale. Dupa fiecare etapa de ameliorare, relatiile din baza de date ating un anumit grad de perfectiune, deci se afla intr-a anumita forma normala.

Trecerea unei relatii dintr-o forma normala in alta, presupune eliminarea unui anumit tip de dependente nedorite, care sunt transformate in dependente care nu provoaca anomalii (admisibile).

Procesul de ameliorare trebuie sa satisfaca cerintele:

sa garanteze conservarea datelor

sa garanteze conservarea dependentelor dintre date

sa reprezinte o descompunere minimala a relatiilor initiale.

Necesitatea normalizarii deriva din problemele generate de anomalii. Anomaliile care apar in lucrul cu baze de date se produc datorita dependentelor care exista intre datele bazei de date. Exista anomalii:

la inserare de date

la modificare / stergere

redundanta in date (aparitii repetate)

probleme de reconexiune.

Normalizarea permite:

suprimarea redundantei logice

evitarea anomaliilor la reactualizare

rezolvarea problemei reconexiunii.

Exista o teorie matematica a normalizarii, al carei autor este E. F. Codd, conform careia, se construiesc tabele standard (forme normale).

Orice forma normala se obtine aplicand o schema de descompunere. Exista 2 tipuri de descompuneri:

descompuneri ce conserva dependentele ( descompunerea unei relatii R in proiectii R₁, ., R_k:    )

descompuneri fara pierderi de informatie ( regula lui Casey-Delobel).

Regula Casey-Delobel

Fie R(A) o schema relationala si α, β, γ o partitie a lui A. Presupunem ca α determina functional pe β. Atunci:

, unde αUβ este multime atributelor care intervin in dependentele functionale si αUγ este reuniunea determinantului cu restul atributelor lui A.

Formele normale ale relatiilor dintr-o baza de date relationala sunt definite in raport cu anomaliile care pot aparea in lucrul cu aceste relatii.

Prima forma normala (FN 1)

O relatie este in FN 1 daca fiecarui atribut care o descompune ii corespunde o valoare indivizibila (atomica). Un tuplu nu trebuie sa contina atribute sau grupuri de atribute repetitive.

Algoritmul AFN-1 care aduce o relatie in FN 1 elimina atributele compuse si cele repetitive.

Forma normala 2 (FN 2)

O relatie este in FN 2 daca si numai daca:

o       Relatia R este in FN 1

o       Fiecare atribut care nu este cheie (nu participa la cheia primara) este dependent de intreaga cheie primara.

Pentru a obtine o relatie in FN 2 se poate aplica regula Casey-Delobel: fie relatia R(k₁, k₂, x, y), k₁, k₂ definesc cheia primara, x si y sunt multimi de atribute astfel incat k₁ x ( rezulta ca R nu este in FN 2). Solutia este inlocuirea lui R cu doua proiectii R₁(k₁, k₂, y) si R₂(k₁, x).

Algoritmul AFN-2 de aducere a unei relatii in FN 2 elimina dependentele functionale partiale din cadrul unor relatii aflate in FN 1.

Forma normala 3 (FN 3)

O relatie R este in FN 3 daca si numai daca:

o       Relatia R este in FN 2

o       Fiecare atribut care nu este cheie (nu participa la o cheie) depinde direct de cheia primara.

Din punct de vedere formal, o relatie R este in FN 3 daca si numai daca:

o       Relatia R este in FN 2

o       Fiecare atribut care nu este cheie (nu participa la o cheie) nu este dependent tranzitiv de nici o cheie a lui R.

Definitie: (A este dependent tranzitiv de X

Fie R o relatie, X o submultime de atribute ale lui R si A un atribut al relatiei R. A este dependent tranzitiv de X daca: y astfel incat x y si y A (A y si y nu determina pe X).

Pentru a obtine o relatie FN 3 se poate aplica regula de descompunere Casey-Delobel.

Algoritmul AFN-3 pentru aducerea unei relatii FN 2 in FN 3 elimina dependentele functionale tranzitive.

Forma normala Boyce_Codd(BCNF)

O relatie R este in forma normala Boyce-Codd daca si numai daca fiecare determinant este o cheie candidat (sau pentru orice dependenta functionala totala X A, X este o cheie a lui R).

Algoritmul ABCNF pentru aducerea unei relatii in BCNF elimina dependentele functionale ai caror determinanti nu sunt chei candidat.

Forma normala 4 (FN 4)

O relatie BCNF este in FN 4 daca pentru orice multidependenta elementara de forma X Y, X este o supercheie a lui R.

Aducerea relatiilor in FN 4 presupune eliminarea dependentelor multivaloare atunci cand sunt mai mult de una in cadrul unei relatii.

Forma normala 5 (FN 5)

Relatia R este in FN 5 daca si numai daca:

o       Relatia R este in FN 4

o       Nu contine dependente ciclice.

Algoritmul AFN-5 pentru aducerea unei relatii FN 4 in FN 5 elimina join-dependentele.

Exemplu:

R = JOIN (JOIN(R₁, R₂), R₃)