Modele cu transfer direct (tip I-E)

Modele cu transfer direct (tip I-E)

Modelul obiect de tip transfer intrare-iesire ('input-output transfer') al unui sistem liniar continuu monovariabil se construieste pe baza vectorilor linie num=[b_n b_n-1 b₁ b₀] si den=[a_n a_n-1 a₁ a₀], formati cu coeficientii derivatelor intrarii, respectiv cu coeficientii derivatelor iesirii din ecuatia diferentiala standard

a_ny⁽ⁿ⁾+a_n-1y^(n-1)++a₁y'+a₀y = b_ru^(r)+b_r-1u^(r-1)++b₁u'+b₀u ,

sau din functia de transfer

.

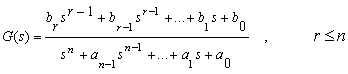Modelul se construieste cu functia tf astfel

stf = tf (num,den);

Ca argument de intrare, vectorul num poate fi scris, in cazul r <n, si sub forma num=[b_r b_r-1 b₁ b₀].

Din modelul stf se pot extrage matricele num si den, fie cu ajutorul functiei

[num,den]=tfdata(stf);

fie prin referire directa la proprietatile obiectului model:

num=stf.num; den=stf.den;

Ultima cale permite, de asemenea, modificarea proprietatilor modelului stf:

stf.num=num1; stf.den=den1;

sau chiar

stf.num(i)=b_n-i+1; stf.num(i)=a_n-i+1;

Modelul sistemului static cu G(s)=k se poate construi cu comanda simplificata

stf = tf (k);

Daca sistemul are timpul mort tm, adica , atunci modelul se construieste fie cu functia tf:

stf = tf (num,den,'iodelay',tm);

fie cu proprietatea modelului

stf.iodelay=tm;

n

In cazul sistemelor continue multivariabile (MIMO), modelul poate fi obtinut prin concatenarea modelelor monovariabile (SISO). De exemplu, modelul corespunzator matricei de transfer

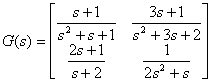
poate fi construit, prin concatenare, astfel:

s11=tf([1 1],[1 1 1]);

s12=tf([3 1],[1 3 2]);

s21=tf([2 1],[1 2]);

s22=tf(1,[2 1 0]);

stf=[s11 s12;s21 s22];

De asemenea, modelul poate fi construit prin crearea a doua multimi de vectori linie asociati numaratorilor si numitorilor tuturor functiilor de transfer din componenta lui G(s):

Num=;

Den=;

stf=tf(Num,Den);

Modelul sistemului static cu poate fi construit astfel

stf=tf([1 2;3 4]);

Comanda

s1=stf(i,j);

extrage subsistemul cu intrarea j si iesirea i, adica cu functia de transfer G_ij(s).

Comenzile

[num,den]=tfdata(stf); n1=num; d1=den;

extrag vectorii numarator n1 si numitor d1 ai subsistemului monovariabil cu intrarea j si iesirea i, adica cu functia de transfer G_ij(s).

Comenzile

n1=stf.num; d1=stf.den;

realizeaza acelasi lucru pe baza proprietatilor modelului stf.

Comenzile

stf.num=n1; stf.den=d1;

sau chiar

stf.num(k)=b_n-k+1; stf.den(k)=a_n-k+1;

permit modificarea proprietatilor modelului stf.

Daca sistemul are timp mort, adica

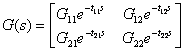
atunci modelul cu timp mort se poate construi din modelul fara timp mort, astfel

stf.iodelay=[t11 t12;t21 t22];

n

Modelul de tip transfer direct al unui sistem liniar discret cu modelul standard

y(t)+ a₁y(t-1)+ + a_ny(t-n)= b₀u(t)+ b₁u(t-1)+ + b_ru(t-r)

se construieste pe baza vectorilor linie num=[b₀ b₁ b_n] si den=[a₀ a₁ a_n] formati cu coeficientii termenilor intrarii, respectiv cu coeficientii termenilor iesirii. In acest scop, se utilizeaza functia filt:

stf = filt(num,den,T);

sau functia tf:

stf = tf (num,den,T,'variable','z^-1');

unde T este perioada de esantionare.

Daca b₀=b₁=.=b_j=0, atunci argumentul de intrare num poate fi utilizat si sub forma num=[b_j+1 b_j+2 b_n]. In cazul r >n, vectorul den se scrie sub forma den=[a₀ a₁ a_n 0 . 0], astfel incat sa aiba dimensiunea r +1.

Din modelul sis se pot extrage matricele num si den ca la sistemele continue, cu ajutorul functiei tfdata sau prin referire directa la proprietatile obiectului model.