Utilizarea matlab pentru analiza sistemelor dinamice in domeniul timp si frecventa

Utilizarea MATLAB pentru analiza sistemelor dinamice in domeniul timp si frecventa

Scopul lucrarii

Lucrarea prezinta principalele facilitati ale pachetului Control System Toolbox din Matlab pentru analiza raspunsurilor in timp si frecventa ale sistemelor dinamice liniare.

Obtinerea raspunsului in timp al sistemelor liniare permite analiza comportarii tranzitorii a acestora pentru diverse tipuri de intrari exogene (referinte si perturbatii), sau daca este cazul, a unor sisteme de reglare automata. Pot fi analizate astfel: timpul tranzitoriu, timpul de crestere, suprareglajul, eroarea stationara la referinta treapta, etc. Raspunsul in timp al sistemelor se determina prin intermediul functiei de transfer a sistemului (procesului) considerat.

Raspunsul in frecventa este reprezentarea raspunsului sistemului la intrari sinusoidale de frecvente diferite. Iesirea unui sistem liniar pentru o intrare sinusoidala este o sinusoida de aceeasi frecventa, dar de amplitudine si faza diferita. Raspunsul in frecventa este definit pe baza diferentei de amplitudine si de faza intre cele doua sinusoide, de intrare si de iesire. Raspunsul in frecventa al sistemului in circuit deschis poate fi folosit pentru aprecierea comportarii sistemului in circuit inchis.

2. Consideratii teoretice

Se considera un sistem dinamic pentru care se definesc intrarea u(t) si iesirea y(t) (figura 1).

Fig. 1

Transformata Laplace a functiei (raspunsului) pondere a unui sistem liniar

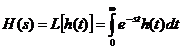(1)

se numeste functia de transfer a sistemului respectiv. Functia de transfer e definita ca raportul transformatelor Laplace ale marimilor de iesire si intrare:

(2)

in conditii initiale nule. Aceasta definitie pune in evidenta faptul ca functia de transfer este independenta de marimea de intrare si depinde numai de "proprietatile interne" ale sistemului.

Utilizarea transformatei Laplace are o serie de avantaje procedurale care deriva din transferarea problemelor din domeniul calculului diferential in cel al calculului algebric. Consideram in continuare modelul unui proces liniar, invariant, reprezentat in figura 1, cu intrarea u(t) si iesirea y(t) scalare. Modelul procesului liniar poate fi exprimat printr-o ecuatie diferentiala liniara, de forma urmatoare:

(3)

unde coeficientii a_i, b_j, i= 0, ,,,n, j = 1, ., m sunt parametri constanti reali.

Relatia (2) permite gasirea functiei de transfer direct din ecuatia diferentiala. Utilizand teorema derivarii originalului si aplicand transformata Laplace in ambii membri ai ecuatiei diferentiale (3) (cu a_n = 1), obtinem in conditii initiale nule:

(4)

Un proces descris de o ecuatie diferentiala liniara cu coeficienti constanti are deci o functie de transfer rationala.

Functiile de transfer ale unor elemente tip sunt urmatoarele:

Elementul de intarziere de ordinul I

unde k = b₀ / a_o este factorul de proportionalitate, T = a₁ / a₀ este constanta de timp.

Elementul integrator

Elementul de ordinul II

unde z este factorul de amortizare, w_n este pulsatia naturala.

Modelele unor procese (de exemplu, cele cu "timp mort") pot fi reprezentate si prin alte tipuri de functii de transfer, cum ar fi:

Elementul cu timp mort

Elementul de intarziere de ordinul I cu timp mort

Daca transformata Laplace U(s) a functiei de intrare este o functie rationala, atunci si Y(s) este o functie rationala. In acest caz, functia de iesire y(t) (raspunsul in timp al sistemului) se gaseste prin aplicarea transformarii inverse Laplace:

(5)

utilizand metoda reziduurilor sau descompunerea in fractii simple.

Control System Toolbox ofera functii pentru obtinerea raspunsului la intrare de tip treapta, impuls, in continuu sau discret utilizand functia de transfer a unui proces (sistem dinamic).

Raspunsul in frecventa al unui sistem liniar cu functia de transfer in circuit deschis H_d(s) este definit ca fiind:

(6)

Raspunsul in frecventa poate fi reprezentat in doua moduri: sub forma de diagrama Bode (caracteristici logaritmice de frecventa figura 2a)) sau diagrama Nyquist (locul de transfer sau hodograful, figura 2b)). Ambele metode permit obtinerea aceleiasi informatii, diferenta consta in modul in care este prezentata aceasta informatie. Pentru a trasa caracteristicile de frecventa in reprezentare logaritmica (Bode) se creeaza un vector de frecvente cu ajutorul functiei Matlab logspace si se calculeaza valorile functiei de transfer |H_d(jw)| la aceste frecvente prin apelul functiei Bode (conform ecuatiei (6)). Se reprezinta |H_d(jw)|_dB in functie de frecventa.

Similar se pot reprezenta si caracteristicile de tip loc de transfer Nyquist prin apelul functiei Matlab cu acelasi nume - nyquist(num, den, w).

In analiza de frecventa se mai definesc:

marginea de amplitudine sau de "amplificare" a sistemului in circuit deschis

(7)

unde w_p este pulsatia pentru care arg(H_d(jw p (adica Im(H_d(jw

marginea de faza a sistemului in circuit deschis

(8)

unde w_c este pulsatia pentru care |H_d(jw

Analiza stabilitatii sistemului in circuit inchis se poate face pe baza caracteristicilor de frecventa ale sistemului in circuit deschis, A(w) = |H_d(jw)| si j w) = arg(H_d(jw)). Putem defini doua caracteristici logaritmice de frecventa (Bode):

caracteristica amplitudine (atenuare) / pulsatie

(9)

(10)

caracteristica faza / pulsatie

(11)

Fig. 2 a) Caracteristicile de frecventa amplitudine/pulsatie si faza/pulsatie,

b) Locul de transfer

Control System Toolbox ofera functii pentru trasarea caracteristicilor logaritmice de frecventa. Aceste functii disponibile in Matlab sunt urmatoarele:

3. Desfasurarea lucrarii

In lucrare se vor analiza raspunsurile in timp si frecventa ale sistemelor liniare.

3.1 Obtinerea raspunsului in timp al sistemelor liniare

Se considera sistemul liniar reprezentat prin functia de transfer:

(12)

se defineste functia de transfer prin vectorii coeficientilor numaratorului si numitorului (num si den) pentru diferite valori ale parametrilor z si w_n

omega = 1;

zeta1 = 0; zeta2 = 0.5;

zeta3 = 1; zeta4 = 3;

num = [omega^2];

den1 = [1 2*zeta1*omega omega^2];

den2 = [1 2*zeta2*omega omega^2];

den3 = [1 2*zeta3*omega omega^2];

den4 = [1 2*zeta4*omega omega^2];

se obtine raspunsul indicial (raspunsul la intrare treapta), figura 3

t = 0:0.1:35;

y1 = step(num, den1, t);

y2 = step(num, den2, t);

y3 = step(num, den3, t);

y4 = step(num, den4, t);

se obtine raspunsul la impuls (figura 4)

y_imp = impulse(num, den2, t);

figure(1)

pos = get(1, 'Position');

set(1,

'Position', [pos(1) pos(2) 600 400],

'NumberTitle', 'off',

'Name', 'Raspuns indicial')

plot(t,y1,t,y2,t,y3, t, y4)

grid

title('Raspuns indicial sistem ordin II')

xlabel('Timp')

figure(2)

pos = get(2, 'Position');

set(2,

'Position', [pos(1) pos(2) 600 400],

'NumberTitle', 'off',

'Name', 'Raspuns la impuls')

plot(t, y_imp), grid

title('Raspunsul la impuls al sistemului de ordinul II')

xlabel('Timp')

se determina raspunsul in timp pentru intrari oarecare (de exemplu, sinusoidale)

omega = 0.3;

num = 1;

den = [1 0.5 1];

t = 0:0.1:100;

u = sin(omega*t); % intrare sinusoidala

y = lsim(num, den, u, t);

plot(t,y,'b',t, u, 'r')

axis([50, 100, -2, 2])

se determina raspunsul echivalentului discret al sistemului reprezentat de ecuatia (12) la intrare de tip treapta unitara

[numd, den2d] = c2dm(num, den2, 0.1, 'zoh');

N = 351;

y2_d = dstep(numd, den2d, N);

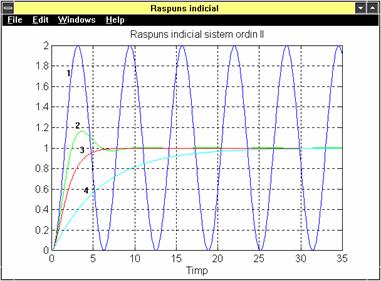
Fig. 3 Raspunsul indicial al sistemului de ordinul II

1) raspuns neamortizat oscilant (x

2) raspuns oscilant amortizat (x

3) raspuns amortizat critic (x

4) raspuns aperiodic (x

Fig. 4 Raspunsul la impuls al sistemului

de ordinul II

3.2 Obtinerea raspunsului in frecventa al sistemelor liniare

Se considera sistemul liniar continuu invariant in timp reprezentat prin urmatoarea functie de transfer:

(13)

Se traseaza caracteristicile logaritmice de frecventa si se calculeaza marginea de faza Pm (Phase margin) si marginea de amplificare Gm (Gain margin):

num = 50; % coeficientii polinomului de la numaratorul functiei de

% transfer

den = [1 9 30 40]; % coeficientii polinomului de la numitorul

% functiei de transfer

w = logspace(-1, 2); % intervalul de frecvente intre care se face

% trasarea caracteristicii

[ampl, faza] = bode(num, den,w); % calculul caracteristicilor

% logaritmice de frecventa

subplot(211), loglog(w, ampl), grid

title('Caracteristica amplitudine - pulsatie')

subplot(212), semilogx(w, faza), grid

title('Caracteristica faza - pulsatie')

xlabel('Pulsatia (scara logaritmica)')

val = [w; ampl'; faza'];% pentru determinarea marginii de amplitudine

% si marginii de faza trebuie a fi

% determinate frecventele w_c si w_p si

% valorile lui A(w) si j w

margin(50, [1 9 30 40]) % calculeaza direct marginile de amplitudine

% si de faza precum si pulsatiile w_p

% respectiv w_c (figura 5)

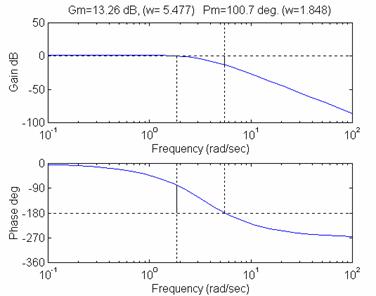
Fig. 5

Determinarea largimii de banda a sistemului in circuit inchis

In regim stationar cu semnale de referinta sinusoidale de frecventa variabila se impune performanta largimii de banda w_B, care exprima caracteristica de filtru trece jos a sistemului in circuit inchis, valoarea w_B corespunzand relatiei (14):

(14)

respectiv relatiei

(15)

unde H₀(s) este functia de transfer a sistemului in circuit inchis.

Se considera urmatoarea functie de transfer:

se reprezinta sistemul in MATLAB

> num = [1];

> den = [1 0.5 1];

se determina largimea de banda din diagrama Bode (figura 6)

> bode(num, den)

Fig. 6

Pentru sistemul in circuit inchis considerat se obtine largimea de banda egala cu aproximativ 1.4 rad/s (frecventa corespunzatoare unei amplificari de -3 db).

Se simuleaza raspunsul sistemului pentru frecvente mai mici, respectiv mai mari decat largimea de banda:

a.        pentru o frecventa de intrare de aproximativ 0.3 rad/s

w = 0.3;

num = 1;

den = [1 0.5 1];

t = 0:0.1:100;

u = sin(w*t);

y = lsim(num, den, u, t);

plot(t,y,'w-',t,u,'y--')

axis([50, 100, -2, 2])

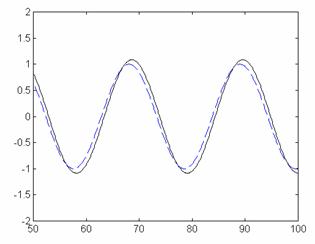
Fig. 7a)

b.       pentru o frecventa de intrare de aproximativ 3 rad/s

w = 3;

num = 1;

den = [1 0.5 1];

t = 0:0.1:100;

u = sin(w*t);

y = lsim(num, den, u, t);

plot(t,y,'w-',t,u,'y--')

axis([90, 100, -1, 1])

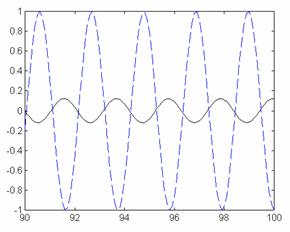
Fig. 7b)

3.3 Trasarea caracteristicilor de frecventa pentru procese cu timp mort

Se considera un proces de ordinul intai cu timp mort reprezentat prin urmatoarea functie de transfer:

(16)

Pentru simularea acestui sistem se vor executa urmatorii pasi:

a.        reprezentarea procesului si a domeniului de frecvente:

kf = 1.5;

tf = 10;

tau = 20;

num1 = [0 kf];

den1 = [tf 1];

w = logspace(-5, 0.5, 70);

b.       calculul raspunsului in frecventa pe intervalul de frecvente considerat

g1 = freqresp(num1, den1, sqrt(-1)*w);

c.        calculul realului si imaginarului pentru procesul fara timp mort, H'_d(s)

x1 = real(g1);

y1 = imag(g1);

d.       calculul caracteristicilor logaritmice de frecventa pentru procesul fara timp mort, H'_d(s)

[a, fi] = bode(num1, den1, w);

e.        calculul caracteristicilor de frecventa si al hodografului pentru procesul cu timp mort, H_d(s)

for i=1:length(w)

%calculeaza Re1 si Im1 pentru H'd fara timp mort

Re1(i) = x1(i);

Im1(i) = y1(i);

% calculeaza Re2 si Im2 pentru Hd cu timp mort

Re2(i) = Re1(i)*cos(w(i)*tau) + Im1(i)*sin(w(i)*tau);

Im2(i) = -Re1(i)*sin(w(i)*tau) + Im1(i)*cos(w(i)*tau);

% cercul de raza unitate

x3(i) = sin(w(i));

y3(i) = cos(w(i));

% caracteristica amplitudine (atenuare) / pulsatie

marg_amplit(i) = a(i);

% caracteristica faza / pulsatie

marg_faza(i) = fi(i) - w(i)*tau*360/3.14;

modul_Hd(i) = sqrt(Re2(i)^2 + Im2(i)^2);

arg_Hd(i) = (180/3.14)*atan(Im2(i)/Re2(i));

end;

f.         afisarea rezultatelor (figura 8)

subplot(311), loglog(w, marg_amplit), title('Caracteristica amplitudine / pulsatie'), grid

subplot(312), semilogx(w, marg_faza), title('Caracteristica faza / pulsatie'), grid

subplot(313), plot(Re2(1:1:60), Im2(1:1:60),'g'), title('Locul de transfer (hodograful)'), grid

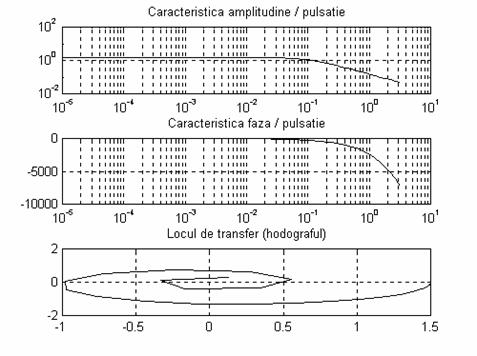
Fig. 8 Caracteristicile logaritmice de frecventa si hodograful

unui proces de ordinul I cu timp mort

Se considera un proces cu timp mort pur reprezentat prin urmatoarea functie de transfer:

(17)

Se foloseste urmatoarea secventa de instructiuni Matlab pentru obtinerea caracteristicilor logaritmice de frecventa si a hogografului (figura 9):

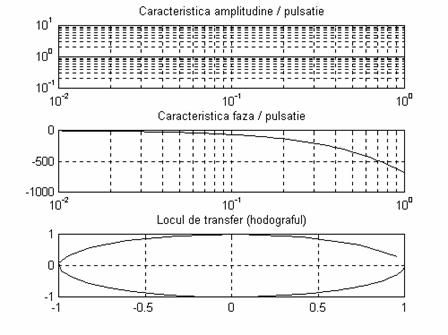
Fig. 9

4. Continutul referatului

Referatul va contine

Sa se realizeze simularile corespunzatoare punctelor 3.1, 3.2 si 3.3 pentru analiza in timp si frecventa. Sa se analizeze rezultatele obtinute. Apreciati |H| si j la frecventele respective (figurile 7a si 7b), comparati-le cu valorile rezultate din figura 6.

Cum influenteaza modificarea factorului de proportionalitate in regim stationar forma caracteristicilor de frecventa (figura 5)? Considerati factor de proportionalitate mai mare de 100 ori.

Sa se analizeze comportarea in timp si in frecventa a sistemului de ordinul I, avand functia de transfer pentru diferite valori ale parametrilor (k =1, k = 10; T = 1 secunda, T = 10 secunde).