| CATEGORII DOCUMENTE |
| Animale | Arta cultura | Divertisment | Film | Jurnalism | Muzica |
| Pescuit | Pictura | Versuri |
RETELE NEURONALE BAZATE PE PERCEPTRON
1 Perceptronul multistrat
Am vazut in capitolul trecut, ca perceptronul singur nu poate rezolva problema XOR, datorita faptului ca in acest caz, cele doua multimi de puncte nu sunt liniar separabile.

Problema XOR poate fi descompusa in doua probleme liniar separabile, rezolvabile cu ajutorul perceptronului (fig. 1).
Prima problema, care este o problema AND (fig. 1a) , poate fi rezolvata cu ajutorul unui perceptron, numerotat cu indicele 1, avand w11 w12 si q , deci dreapta de separatie va avea ecuatia x1 + x2 - 1.5 = 0. Pentru punctele de coordonate (0,0), (0,1) si (1,0) iesirea perceptronului va avea valoarea 0, iar pentru punctul de coordonate (1,1), iesirea va avea valoarea 1.
A doua problema (fig. 1b) este rezolvabila cu ajutorul unui perceptron, notat cu indicele 2, avand w21 w22 si q deci dreapta de separatie va avea ecuatia x1 + x2
Pentru rezolvarea problemei XOR, va trebui utilizat un alt perceptron, care sa construiasca o combinatie liniara a marginilor de decizie formate de primii doi perceptroni. Acest perceptron va avea ca intrari iesirile celorlati 2, iar o posibila solutie pentru ponderi si valoarea de prag este w31=-2; w32=1; q . Se obtine astfel o retea neuronala cu doua straturi, numita retea conectata inainte (engl: feed-forward network), sau perceptron multistrat (fig. 2).
O retea neuronala conectata inainte se compune din 3 sau mai multe straturi. Primul strat, numit strat de intrare, este format din conexiunile de intrare ale neuronilor din stratul Acest strat nu are rol de calcul, realizand doar preluarea si dispecerizarea semnalelor de intrare. Neuronii de intrare formeaza un strat ascuns. Iesirile lor sunt conectate pe intrarile unor neuroni din alt strat ascuns, sau din stratul de iesire.
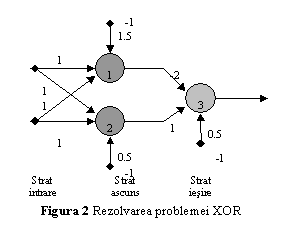
Functionarea retelei este simpla.
Neuronul 2 este conectat la neuronul 3 prin intermediul unei sinapse cu
conexiune pozitiva, deci are un efect excitator. Neuronul 1 este conectat la
neuronul 3 prin intermediul unei sinapse cu o pondere negativa, deci va avea un
efect inhibitor. Cum aceasta pondere este mai mare decat ponderea neuronului 2,
efectul inhibitor va fi mai puternic decat cel excitator.
Daca intrarea retelei este punctul de coordonate (0,0), ambii neuroni din stratul ascuns vor avea iesirea 0, deci si iesirea neuronului 3 va fi 0. Pentru punctul (1,1), iesirile ambilor neuroni din stratul ascuns vor fi 1, dar cum efectul inhibitor este preponderent, iesirea neuronului 3 va ramane la 0. Pentru ambele puncte (0,1) si (1,0), iesirea neuronului 1 este 0 iar iesirea neuronului 2 va fi 1. Cum neuronul 2 are un efect excitator, pentru aceste puncte, iesirea neuronului 3 va fi 1.
2 Algoritmul de antrenare cu propagarea inapoi a erorii
In exemplul din paragraful precedent, reteaua neuronala conectata inainte are ponderile sinaptice si functiile de prag ale fiecarui neuron astfel fixate, incat sa rezolve o problema propusa. In mod normal, o astfel de retea isi adapteaza ponderile in decursul unei faze de antrenare, fiind capabila la sfarsitul acesteia sa obtina solutiile problemei pentru care a fost antrenata, sau, sa le generalizeze, in cazul in care primeste pe intrare stimuli ce nu fac parte din setul stimulilor de antrenare.
Cel mai des utilizat algoritm de antrenare pentru retelele conectate inaine este algoritmul de antrenare cu propagarea inapoi a erorii. Acest algoritm rezolva problema antrenarii de o maniera supervizata, fiind compus din doua faze:
o faza de propagare inainte, in care un set de vectori sablon sunt aplicati pe intrarea retelei, iar efectul acestora se propaga inainte de la neuron la neuron, prin fiecare strat al retelei, producand un raspuns la nivelul neuronilor din stratul de iesire;
o faza de propagare inapoi, in care semnalul de eroare (datorat diferentei raspunsului real al retelei la un anumit stimul fata de raspunsul dorit) este propagat inapoi in retea, pe baza acestuia si in acord cu un anumit algoritm realizandu-se modificarea ponderilor sinaptice, astfel incat semnalul de eroare sa fie minimizat.
Pentru descrierea algoritmului de antrenare, vom considera urmatoarele:
fiecare neuron al retelei neuronale contine o functie de prag neliniara, diferentiabila in orice punct. Vom considera ca functie de prag functia sigmoida unipolara, sau functia logistica, de forma
![]() (1)
(1)
unde vk este potentialul intern al neuronului k, iar yk iesirea acestui neuron;
reteaua contine unul sau mai multe straturi scunse, care nu comunica cu exteriorul, nici ca semnale de intrare, nici ca semnale de iesire. Aceste straturi ascunse permit retelei sa invete sa rezolve probleme mai complexe;
reteaua este total conectata, in sensul ca fiecare neuron al unui strat este conectat cu intrarile tuturor neuronilor din stratul urmator (fig. 3a);
In interiorul retelei, in faza de antrenare, pot fi puse in evidenta doua tipuri de flxuri de semnale:
semnale functionale, care sunt semnale de intrare aplicate la o intrare a unui neuron, se propaga din neuron in neuron inainte in retea, si produc un semnal de iesire. Le vom numi semnale functionale, pentru ca prin intermediul lor este pusa in evidenta functionarea retelei, si in plus, ele sunt modificate in functie de ponderile asociate intrarilor neuronilor pe care ii traverseaza;
semnale de eroare, care se propaga in sens invers (de la iesire spre intrare) in retea, parcurgand fiecare neuron. Aceste semnale depind de modul de evaluare a erorii dintre valoarea reala a semnalului de iesire din retea si valoarea dorita a acestuia (fig. 3b)
Dupa terminarea antrenarii, fluxul semnalelor de eroare este sistat, ramanand doar fluxul semnalelor functionale.

Fiecare neuron
din straturile ascunse sau din stratul de iesire executa doua operatii de
calcul:
calculul semnalului de iesire, ca expresie a functiei neliniare continue aplicate asupra sumei semnalelor de intrare ponderate prin intermediul ponderilor sinaptice;
calculul valorii instantanee al gradientului pe suprafata de eroare corespunzatoare intrarilor neuronului, necesar in faza de adaptare a ponderilor neuronului
Vor fi utilizate urmatoarele notatii:
indicii k, m, n vor pune in evidenta diferiti neuroni din retea. Pentru a indica pozitia exacta in retea, vom considera ca neuronul m se afla intr-un strat la dreapta stratului in care se afla neuronul k, iar daca neuronul m nu este de iesire, neuronul n se va afla intr-un strat la dreapta acestuia;
iteratia j se refera la al j-lea sablon de antrenare prezentat la intrarea retelei;
iesirea ym(j) reprezinta semnalul de iesire al neuronului m la iteratia j;
wmk(j) reprezinta valoarea ponderii sinaptice ce leaga iesirea neuronului k cu intrarea neuronului m, la iteratia j. In faza de antrenare, aceasta pondere sinaptica poate fi modificata cu valoarea D wmk(j);
potentialul intern al neuronului m la iteratia j este notat cu vm(j);
functia de activare neliniara a neuronului m este notata prin jm
valoarea de prag asociata neuronului m este notata cu qm. Aceasta valoare de prag este obtinuta prin conectarea la valoarea -1 a unei sinapse cu ponderea wm0 qm
elementul k al sablonului de intrare prezentat la iteratia j este specificat prin xk(j);
elementul n al vectorului de iesire al retelei (compus din iesirile tuturor neuronilor din stratul de iesire) la iteratia j este notat prin on(j);
rata de invatare, considerata in aceasta faza ca fiind un numar constant, pozitiv si mic, este notata cu h
valoarea dorita a iesirii neuronului m la iteratia j este notata cu dm(j);
semnalul de eroare la iesirea neuronului m la iteratia j este notat cu em(j);
La iteratia j, deci, la aplicarea celui de al j-lea sablon de antrenare, semnalul de eroare la iesirea neuronului m va fi dat de
![]() (2)
(2)
Semnalele de eroare pot fi puse in evidenta doar pentru neuronii din stratul de iesire, acestia fiind singurii "vizibili" din exteriorul retelei. Pentru stratulde iesire, se poate calcula eroarea patratica instantanee, la iteratia j, ca suma tuturor erorilor patratice ale neuronilor din acest strat, adica:
![]() (3)
(3)
unde O este multimea tuturor neuronilor din stratul de iesire. Considerand ca in procesul de antrenare retelei ii sunt prezentate N sabloane de antrenare, se poate calcula eroarea patratica medie pentru intreg setul de sabloane
![]() (4)
(4)
Valorile erorilor patratice instantanee si a erorii patratice medii, depind de toti parametrii liberi ai retelei, adica de ponderile sinaptice si de valorile de prag ale fiecarui neuron. Cum, scopul urmarit este de a obtine raspunsuri cat mai apropiate de cele dorite pentru tot setul de sabloane, eroarea patratica medie poate fi utilizata ca si indice de performanta ce trebuie minimizat in cursul antrenarii. Pentru minimizarea acestui indice, ponderile sinaptice vor fi modificate astfel incat, gradientul erorii sa alunece" pe suprafata de eroare, pana la atingerea minimului. Cum valorile semnalelor de eroare pot fi puse in evidenta doar pentru neuronii din stratul de iesire, va trebui sa gasim o modalitate de exprimare a erorilor la iesirile neuronilor ascunsi in functie de acestea, deci de ajustare a ponderilor lor.
Potentialul intern al neuronului m va fi dat de relatia
![]() (5)
(5)
unde p este numarul intrarilor neuronului m, mai putin intrarea de prag. Deci, semnalul de iesire al neuronului m la iteratia j, va fi dat de:
![]() (6)
(6)
Adaptarea ponderii sinaptice wmk(j) cu valoarea Dwmk(j) se face proportional cu valoarea instantanee a gradientului ME(j) Mwmk(j). Valoarea acestui gradient determina directia de cautare in spatiul ponderilor pentru ponderea sinaptica wmk. Se poate scrie:
![]() (7)
(7)
Derivand relatia (3) in raport cu em(j), se obtine
![]() (8)
(8)
Derivand relatia (2) in raport cu ym(j) se obtine
![]() (9)
(9)
Derivand relatia (6) in raport cu vm(j) se obtine
![]() (10)
(10)
Derivand relatia (5) in raport cu wmk(j) obtinem
![]() (11)
(11)
Prin inlocuirea (8), (9), (10) si (11) in (7) se obtine
![]() (12)
(12)
Similar algoritmului de antrenare pentru un singur neuron, corectia Dwmk(j) aplicata ponderii wmk(j) la iteratia j, va fi data de
![]() (13)
(13)
unde semnul specifica descresterea gradientului in spatiul ponderilor. Tinand cont de (12) si (13), corectia aplicata ponderii devine
![]() (14)
(14)
unde dm(j) este gradientul local, definit de
![]() (15)
(15)
Relatiile (2), (14) si (15) permit calcularea imediata a corectiei aplicate asupra ponderii, in ipoteza in care neuronul m apartine stratului de iesire. In acest caz, in mod evident, eroarea instantanee em(j) este usor masurabila, pentru orice iteratie j.
Probleme apar in situatia in care neuronul m apartine unui strat ascuns, caz in care semnalul de eroare este dificil de pus in evidenta, din cauza ca pentru neuronii din stratul ascuns nu este definita o valoare dorita a semnalului de iesire. Fie neuronul m apartinand stratului ascuns. Pe baza relatiilor (7) si (15), se poate redefini gradientul local dm(j) al neuronului m din stratul ascuns la iteratia j ca:
![]() (16)
(16)
Daca neuronul n este un neuron din stratul de iesire, relatia (3) poate fi rescrisa
![]() (17)
(17)
Derivand relatia (17) in raport cu ym(j), se obtine
![]() (18)
(18)
Relatia (18) poate fi scrisa in forma echivalenta
![]() (19)
(19)
Cum neuronul n este un neuron din stratul de iesire, pentru acesta de eroarea en(j) este evaluabila, fiind data de
![]() (20)
(20)
Deci, prin derivare
![]() (21)
(21)
unde, potentialul intern al neuronului n este dat de
![]() (22)
(22)
q fiind numarul total al intrarilor neuronului n, mai putin intrarea de prag. Ponderea wn0=qn este conectata la valoarea -1. Derivand (22) in raport cu ym(j) obtinem
![]() (23)
(23)
Aplicand (22) si (23) in (19), rezulta:
![]() (24)
(24)
unde gradientul local a fost calculat conform relatiei (15), tinand cont ca neuronul n se afla in stratul de iesire. Inlocuind (1.24) in (16), se poate calcula gradientul local dm(j), unde neuronul j apartine stratului ascuns ca:
![]() (25)
(25)
Deci, gradientul local al unui neuron dintr-un strat ascuns, depinde de derivata functiei de activare proprii, precum si de gradientele locale ale tuturor neuronilor din stratul de iesire, ponderate prin intermediul valorilor ponderilor sinaptice ce conecteaza iesirea neuronului curent cu fiecare neuron din stratul de iesire. Tinand cont de faptul ca suntem in faza de propagare inapoi a erorii, deci fluxul de semnale este dinspre stratul de iesire inspre stratul ascuns si ca reteaua este total conectata, deci iesirea fiecarui neuron dintr-un strat este conectata pe intrarea tuturor neuronilor din stratul urmator, rezultatul apare ca si corect.
Calculul corectiei ponderii se face si in acest caz cu ajutorul relatiei (14).
Tinand cont ca, dupa cum am aratat la inceputul paragrafului, se presupune ca neuronii au ca functii de activare functia logistica, relatiile (15) si (25) pot fi dezvoltate in continuare. Presupunand pentru simplitate ca panta functiei logistice este 1, se poate scrie
![]()
Inlocuind in (26) expresia functiei logistice, se obtine
![]() (27)
(27)
Deci, gradientul local pentru neuronul m poate fi calculat ca:
Neuronul m se afla in stratul de iesire. In acest caz notam ym(j)= om(j) si obtinem
![]() (28)
(28)
Neuronul m se afla in stratul intermediar
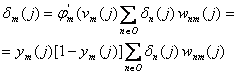 (29)
(29)
Aplicand relatia (14) pentru calculul corectiei, se obtine o generalizare a relatiei (1.32).
Se poate observa ca algoritmul de antrenare presupune doua faze:
o faza in care un vector sablon este aplicat pe intrare, semnalele functionale rezultate propagandu-se inainte in retea, rezultand un vector de iesire pe iesirile neuronilor din stratul de iesire a retelei;
o faza de propagare inapoi, in care semnalele de eroare rezultate in urma compararii vectorului de iesire real cu un vector tinta sunt propagate inapoi in retea, strat cu strat, fiind utilizate la calculul gradientului local pentru fiecare neuron.
Algoritmul de antrenare este aplicat succesiv, pana cand este satisfacut un criteriu de oprire. In general, se considera ca algoritmul de antrenare a indeplinit conditia de antrenare, daca rata absoluta de mnodificare a erorii patratice medii Emed per epoca de antrenare (o epoca de antrenare reprezinta prezentarea intregului set de sabloane de antrenare la intrarea retelei) este mai mica decat e%. Uzual, valoarea lui e este cuprinsa intre 0.1 si 1, in cazuri deosebite putand fi 0.01.
Sintetizind cele aratate anterior, rezulta urmatoarea implementare a algoritmului de antrenare cu propagarea inapoi a erorii:
#define Nr_max=100; // Numarul maxim de epoci de antrenare permise
#define N=Numar_sabloane;
#define Nl=Numar_straturi;
#define Nn[Nl]=Numar_neuroni_per_strat;
int ep=0;
// Pasul 1: Se initializeaza matricea ponderilor
initializeaza matricea ponderilor. Pentru straturile cu neuroni mai putini de Nr_neuroni, ponderile neuronilor care lipsesc se fac 0;
do
}
for(s=Nl;s>0;s--)
for(m=Nn[s];m>0;m--)
// Pasul 4: Faza de propagare inapoi a semnalelor de eroare
calculeaza gradientul local pentru fiecare neuron, strat cu strat
if (s==Nl) ![]()
else ![]()
ajusteaza ponderile sinaptice
![]()
}
// Pasul 5: Evaluarea valorii medii a erorii
calculeaza eroarea patratica medie Emed;
ep++; // numarul de epoci de antrenare se incrementeaza
} while ((Emed >= e) && (ep<Nr_max))
Dupa cum se arata anterior, prezentarea tuturor exemplelor (sabloanelor) de antrenare formeaza o epoca. Daca la sfarsitul unei epoci de antrenare criteriul de oprire (valoarea erorii patratice medii) nu este satisfacut, se trece la o noua epoca de antrenare. Datorita caracterului neliniar al spatiului de cautare, in acest spatiu pot apare puncte singulare de tip ciclu limita. Evolutia cautarii in vecinatatea unui ciclu limita, duce la blocarea convergentei algoritmului. Din acest motiv, se prefera in general prezentarea intr-o ordine aleatoare de la o epoca de antrenare la alta a sabloanelor, ceea ce ofera un caracter stochastic procesului de cautare, evitand intr-o oarecare masura esuarea algoritmului in jurul unui cicle limita.
Algoritmul are doua moduri de aplicare: un mod on-line, numit mod exemplu si un mod off-line, numit mod lot.
In modul exemplu, ponderile sinaptice sunt modidficate dupa prezentarea fiecarei perechi [x(j),d(j)], j=1, ., N. Se prezinta deci exemplul 1, realizandu-se faza de propagare inainte, faza de propagare inapoi, adaptarea ponderilor si calculul erorii, dupa care se prezinta exemplul 2, reluandu-se operatiunile. Se continua pana la finalizarea unei epoci de antrenare. Fie Dwmk(j) corectia aplicata ponderii wmk la prezentarea exemplului j. Corectia globala medie Dw mk calculata pentru intregul set de exemple de antrenare este
![]() (30)
(30)
In modul lot, modificarea ponderilor se face dupa prezentarea intregului lot de exemple. Pentru o epoca oarecare de antrenare, indicele de performanta, luat ca eroarea patratica medie este dat de
![]() (31)
(31)
Pentru o rata de invatare h, corectia aplicata ponderii sinaptice wmk este data de
![]() (32)
(32)
Corectia Dwmk este efectuata dupa prezentarea intregului set de exemple din epoca.
Aproximarea functiilor
Perceptronul multistrat, antrenat cu algoritmul de propagare inapoi a erorii, poate fi vazut la modul general ca o mapare intrare-iesire neliniara.
O serie de cercetatori (Nielsen-Hecht (1987), Cybenko (1989), Hornik (1989) etc.) au aratat ca, perceptronul multistrat poate fi utilizat pentru aproximarea oricarei functii continue. In acest sens, poate fi enuntata urmatoarea teorema (Cybenko, 1989):
Teorema 1 : (Teorema aproximarii universale) Fie j ) o functie marginita, continua, monoton crescatoare. Fie Ip hipercubul unitate p-dimensional [0,1]p. Fie C(Ip) spatiul functiilor continue in Ip. Pentru orice functie f C(Ip) si e > 0, exista un numar intreg M si multimile de constante reale am qm si wmk cu m 1, ., M , k 1, ., p, astfel incat sa se poata defini
![]() (33)
(33)
ca o aproximare a functiei f( ). Adica,
![]() (34)
(34)
Aceasta teorema furnizeaza o justificare matematica pentru aproximarea unei functii arbitrare continue, ca alternativa la reprezentarea exacta a acesteia. Ea este direct aplicabila perceptronului multistrat, tinand cont ca functia logistica ce poate fi utilizata ca functie de activare este continua, marginita si monoton crescatoare. In plus, relatia (33) reprezinta iesirea unui perceptron multistrat, cu urmatoarea structutra:
reteaua neuronala are p noduri de intrare, pe care se aplica semnalele de intrare x1, ., xp si un strat ascuns cu M neuroni;
neuronul m din stratul ascuns are ponderile sinaptice wm1, ., wmp si valoarea de prag qm
iesirea retelei este o combinatie liniara a iesirilor neuronilor din stratul ascuns, parametrii a aM definind aceasta combinatie;
In concluzie, din teorema aproximarii universale se poate deduce ca, orice functie continua, liniara sau neliniara, poate fi aproximata cu o eroare e de un perceptron multistrat, cu un strat ascuns, avand functii de activare logistica pentru neuronii stratului ascuns si respectiv liniara pentru neuronul (neuronii) din stratul de iesire, in domeniul din care este prelevat setul de antrenare.
Aceasta teorema nu precizeaza daca perceptronul cu un singur strat ascuns realizeaza o aproximare optima din punct de vedere a vitezei de convergenta a algoritmului de antrenare sau a finetii de aproximare si nici numarul de neuroni din stratul ascuns necesar pentru realizarea aproximarii. Aceste probleme vor deveni evidente , urmarind exemplele urmatoare.
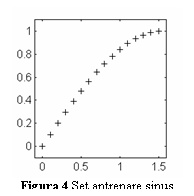
Sa presupunem ca
utilizam un perceptron multistrat pentru a realiza o aproximare a functiei
f(x)=sin(x) in primul cadran. Pentru antrenare, se utilizeaza un set de 16 de
esantioane, ca in fig. 4, utilizand ca set de antrenare perechile (x,f(x)).
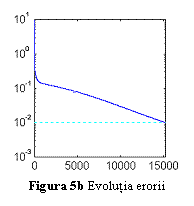
Fig. 5a prezinta
raspunsul initial (marcat cu +) al
unei retele cu un strat ascuns continand 3 neuroni.
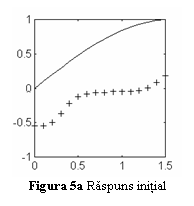
Reteaua este
antrenata cu algoritmul de propagare inapoi a erorii, impunandu-se o eroare
admisibila de 0.01. Evolutia erorii este prezentata in fig. 5b. Dupa 15208
epoci de antrenare, eroarea de scade sub valoarea impusa. Raspunsul retelei
neuronale pentru 32 de valori are variabilei x pe intervalul de antrenare este
prezentat in fig. 6a.
In
fig. 6b si 6c sunt prezentate raspunsurile la cele 32 de valori ale variabilei
x in cazul unei retele cu un strat ascuns cu 10 neuroni si respectiv in cazul
unei retele cu 2 straturi ascunse, avand in aceste straturi 5 si respectiv 3
neuroni.
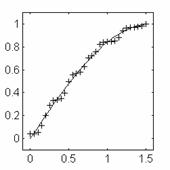 Figura 6b
Retea 10 neuroni
Figura 6b
Retea 10 neuroni
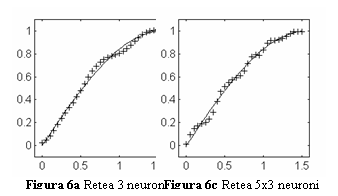
In cel de-al
doilea caz, eroarea admisibila a fost atinsa dupa 23294 epoci de antrenare, iar
in cazul 3 dupa 15103 epoci de antrenare. In figuri, forma functiei sin(x) este
prezentata cu linie continua, iar raspunsul retelei neuronale cu
Este dificil de a se specifica a-priori numarul de straturi ascunse (1 sau 2) ce trebuie utilizate pentru o rezolvare optima a problemei de aproximare si nici numarul de neuroni din stratul ascuns. Exista anumite estimari, cum ar fi cele ale lui Kolmogorov (1957), care precizeaza ca pentru aproximarea unei functii de n variabile, ar fi necesari n(2n+1) neuroni in primul strat ascuns si, in cazul utilizarii a doua straturi ascunse (2n ) neuroni. Cercetari mai recente au aratat insa ca aceste estimari nu conduc intotdeauna la o solutie optima.
Metoda momentului
Algoritmul de antrenare cu propagare inapoi a erorii realizeaza o aproximare in spatiul ponderilor, urmand o traiectorie descendenta a gradientului erorii. Dupa cum s-a aratat anterior, corectia aplicata ponderii depinde de rata de invatare h. Daca acest parametru are valoare mica, urmarirea traiectoriei in spatiul ponderilor se face foarte exact, asigurand o constanta a semnului gradientului. Din pacate, in acest caz, viteza de convergere a algoritmului este foarte scazuta.
Aparent, convergenta algoritmului poate fi crescuta prin utilizarea unei valori mari pentru h. Dar, in acest caz pot apare oscilatii in semnul gradientului (fig. 7a), iar algoritmul de antrenare poate deveni instabil.

O modalitate simpla de a creste rata de invatare in scopul cresterii vitezei de convergenta, fara a apare pericolul intrarii in instabilitate, este adaugarea la relatia de calcul a corectiei ponderii, un termen, numit moment. Corectia va fi calculata astfel dupa relatia
![]() (35)
(35)
unde a este un constanta momentului.
Pentru a vedea care este efectul introducerii termenului moment, sa rescriem corectiile aplicate ponderilor, incepand de la aplicarea primului sablon din epoca de antrenare si pana la sablonul curent:

![]() (36)
(36)
In final, pentru iteratia j se obtine
![]() (37)
(37)
Tinand cont de (12) si (15), relatia (37) poate fi rescrisa ca
![]() (38)
(38)
Conform relatiei (38), corectia aplicata ponderii la iteratia j, apare ca o serie ponderata de un coeficient exponential. Pentru ca aceasta serie sa fie convergenta, este necesar ca
![]() (39)
(39)
Daca a=0, algoritmul functioneaza fara moment.
Daca derivata partiala a erorii nu-si schimba semnul la iteratii consecutive, amplitudinea sumei ponderate Dwmk creste, deci viteza de convergere a algoritmului de antrenare creste.
Daca derivata partiala a erorii isi schimba semnul la iteratii consecutive, amplitudinea sumei ponderate Dwmk scade, deci ponderea va fi ajustata cu o valoare mai mica, evitandu-se intrarea in instabilitate a algoritmului de antrenare.
In spatiul multidimensional neliniar al ponderilor, pot exista puncte de minim local. Daca algoritmul de antrenare incepe (prin initializarea aleatoare a ponderilor) in bazinul de influenta al unui astfel de punct, el va esua in acest minim local, solutia obtinuta nefiind optimala (fig. 7b). Uzual, se incearca evitarea acestor minime locale, prin prezentarea in ordine aleatoare a sabloabnelor de la o epoca la alta. Cum introducerea momentului in algoritmul de antrenare are un oarecare efect de conservare a directiei de evolutie a traiectoriei, anumite valori ale constantei momentului pot avea ca efect temporar urcarea pantei de catre gradient, deci, posibilitatea ca traiectoria sa scape" din bazinul de influenta al minimului local.
Algoritm cu rata de invatare variabila
O alta modalitate de accelerare a convergentei algoritmului de antrenare este utilizarea unei rate de invatare variabile. Pentru a stabili un algoritm de modificare a ratei de invatare, se fac urmatoarele presupuneri:
fiecare parametru al retelei ce poate fi ajustat in cadrul indicelui de performanta va avea asociat un parametru al ratei de invatare propriu;
parametrii ratelor de invatare pot varia de la o iteratie la alta;
daca derivata partiala a indicelui de performanta in raport cu ponderile sinaptice nu isi schimba semnul pentru cateva iteratii consecutive, valoarea parametrului ratei de invatare poate fi crescuta;
daca semnul derivatei partiale a indicelui de performanta in raport cu ponderile sinaptice variaza pentru cateva iteratii consecutive, valoarea parametrului ratei de invatare trebuie scazuta.
Fie hmk(j) parametru ratei de invatare asociat ponderii wmk(j) la iteratia j. Se defineste similar cu (3) indicele de performanta
![]() (40)
(40)
Derivand (40) in raport cu hmk(j), se obtine
![]() (41)
(41)
Relatiile (5) si (13) pot fi rescrise ca
![]() (42)
(42)
![]() (43)
(43)
Inlocuind (43) in (42) rezulta
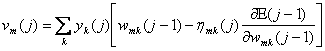 (44)
(44)
Derivand (44) in raport cu hmk(j), se obtine
![]() (45)
(45)
Derivata iesirii in raport cu potentialul intern poate fi evaluata ca
![]() (46)
(46)
Derivand (40) in raport cu ym(j) rezulta
![]() (47)
(47)
Cu acestea, (41) poate fi scrisa ca
![]() (48)
(48)
Inlocuind (12) in (48), se obtine
![]() (49)
(49)
Corectia aplicata coeficientului ratei de invatare respecta algoritmul de descrestere pas cu pas, fiind data de
![]() (50)
(50)
unde g este o constanta pozitiva, numita parametrul de control al pasului. Se pot face urmatoarele observatii:
daca derivata functiei de eroare in raport cu ponderea are acelasi semn la doua iteratii consecutive, Dhmk(j 1) are o valoare pozitiva. Deci, parametrul ratei de invatare creste, crescand implicit viteza de cautare in directia respectiva;
daca derivata functiei de eroare in raport cu ponderea are semne diferite la doua iteratii consecutive, Dhmk(j 1) are o valoare negativa. Deci, parametrul ratei de invatare scade, scazand implicit viteza de cautare in directia respectiva, dar crescand finetea (rezolutia) cautarii.
Implementarea practica a acestui algoritm are in general alta forma, din cauza dificultatii determinarii unei valori corespunzatoare pentru g. Aceasta forma este
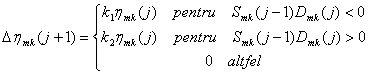 (51)
(51)
unde
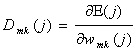 (52)
(52)
si
![]() (53)
(53)
unde k1, k2 si s sunt coeficienti constanti pozitivi.
Sa studiem comparativ cazul unui perceptron multistrat, compus din 5 neuroni in stratul ascuns, avand neliniaritati de tip logistic si un neuron liniar in stratul de iesire, antrenat cu algoritmii de antrenare cu propagare inapoi cu rata de invatare constanta si cu rata de invatare variabila. Reteaua este antrenata sa aproximeze functia f(x)=sin(x) in primul cadran, impunandu-se o eroare maxima de aproximare de 0.01. La fiecare epoca de antrenare retelei ii sunt prezentate 16 esantioane, ca in fig. 4. Fig. 8 prezinta iesirea retelei comparativ cu functia scop, la initializarea ponderilor.
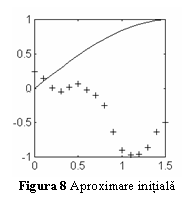
Algoritmul cu
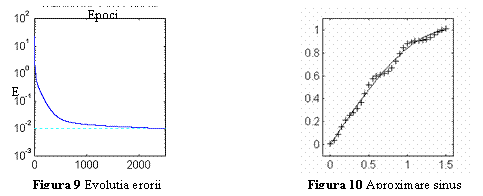
rata de invatare constanta va ajunge la eroarea impusa dupa 2502 epoci de
antrenare. In fig. 9 este prezentata evolutia erorii in cursul antrenarii, iar
in fig. 10 semnalul de iesire a retelei antrenate, care aproximeaza functia
scop, evaluata pentru alte valori ale lui x decat cele la care au fost
prelevate esantioanele utilizate ca sabloane de antrenare.
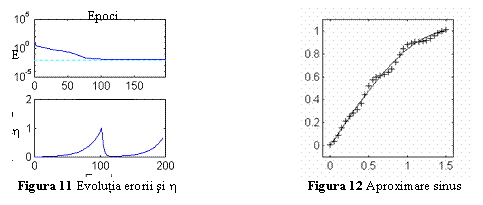
Fig. 11 si 12 prezinta aceleasi informatii in cazul algoritmului de antrenare cu rata de invatare variabila. Se observa modul de variatie a parametrului h si faptul ca aproximarea este similara cazului precedent. Eroarea ajunge sub eroarea admisibila dupa 197 epoci de antrenare.
6 Atrenare bazata pe algoritmi genetici
Algoritmii genetici si-au gasit in ultima perioada utilizarea tot mai larga in rezolvarea problemelor de cautare globala al unui optim. Algoritmii genetici sunt structuri paralele, realizand o tehnica de cautare globala care incearca sa copieze comportamentul operatorilor genetici naturali. Cum algoritmii genetici evalueaza simultan mai multe puncte in spatiul parametrilor, probabilitatea ca algoritmul de cautare sa fie convergent spre punctul de optim global este mult mai mare decat in cazul algoritmului cu propagarea inapoi a erorii.
Algoritmii genetici aplica operatori inspirati din mecanismele naturale de evolutie unor siruri binare care codifica parametrii de cautare. La fiecare generatie, algoritmii genetici exploreaza diferite puncte ale spatiului parametrilor si cauta in regiunile unde probabilitatea cresterii performantelor este mai mare. Cum evaluarea se face pe mai multi indivizi, algoritmii genetici permit cautarea in jurul mai multor puncte de optim local, astfel incat probabilitatea gasirii optimului global este mare. Detalii despre algoritmii genetici pot fi gasite in Anexa 1.
Pentru antrenarea retelelor neuronale, algoritmii genetici vor urma pasii:
Alegerea unei functii de evaluare. Pentru a pastra caracterul de cautare prin cresterea valorii functiei de evaluare, caracteristice algoritmilor genetici, o posibila functie de evaluare a performantei este
![]() (54)
(54)
unde indicele j se refera la care gena din populatie este evaluata, iar Emed(j) reprezinta eroarea patratica medie, calculata conform (4), asociata genei respective. Se poate observa ca pentru valori mari a erorii, valoarea functiei de evaluare tinde spre 0, ea devenind 1 in cazul ideal, pentru eroare nula;
Codificarea retelei in cromozomi si generarea populatiei initiale. O codificare usor de realizat este prin reprezentarea directa a ponderilor si a valorilor de prag pentru fiecare neuron din retea, ca in fig. 13.

Generandu-se aleator un numar de cromozomi, vom obtine o populatie initiala, fiecare reprezentand o retea neuronala;
Se evalueaza un membru al populatei, prin aplicarea setului de sabloane la intrarea retelei neuronale pe care o reprezinta si calcularea valorii functei de evaluare. Se repeta operatia pentru toti membrii;
Se aplica asupra populatiei operatorul de selectie, fiind pastrati un numar de cromozomi pentru reproductie;
Se aplica operatorii de interschimbare si mutatie asupra populatiei de cromozomi parinte, rezultand o noua populatie, de cromozomi fiu;
Daca nu sunt indeplinite conditiile de terminare, se reia pasul 3.
Pentru exemplificare, vom antrena o retea neuronala cu 3 neuroni in stratul ascuns, avand functii de activare logistica si un neuron liniar in stratul de iesire pentrua a aproxima functia f(x) sin(x) in primul cadran.
Genele vor fi reprezentate de numere intregi, in intervalul , avand deci o reprezentare interna pe 16 biti. Pentru a ajunge la valorile ponderilor si valorilor de prag, se va utiliza un factor de scalare 1000, deci elementele retelei vor putea lua valori in intervalul . Se va genera initial o populatie de N de cromozomi, avand fiecare lungimea de 104 biti. S-a ales aceasta varianta, deoarece utilizarea de gene cu valori reale duce in general la cresterea timpului de calcul si a complexitatii implementarii operatorilor de interschimbare si mutatie. Pentru selectie va fi utilizata metoda ruletei. Vor fi alesi P cromozomi;
#define M=Numar maxim mutatii
int Cromozom[N][19];
int Crom_temp[P][19];
int Nr_Generatii=850;
float F_eval[N];
int Ales[P];
int j,k,;
int punct, parinte1, parinte2;
float m;
float sum[N];
// Pasul 1: Se genereaza populatia initiala
randomize();
for (j=0;j<N;j++)
for (k=0;k<19;k++)
Cromozom[j][k]=rand();
do
// Pasul 3: Selectia cromozomilor pentru reproducere
sum[0]=F_eval[0];
for (j=1;j<N;j++) sum[j]=sum[j-1]+F_eval[j];
for (j=0;j<P;j++)
else
realizeaza interschimbarea in cuvantul k, intre cei doi parinti, avand ca pilon octetul l=punct div 16;
j++;
}
// Pasul 6: Mutatie
for(j=0;j<M;j++)
Nr_Generatii
} while (Nr_Generatii);
Nu au mai fost detaliate rutinele care implementeaza interschimbarea si mutatia, acestea fiind relativ usor de conceput.
Solutia obtinuta prin aplicarea algoritmului (cel mai bun cromozom) dupa 850 generatii este:
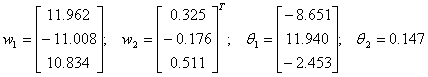
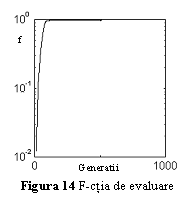
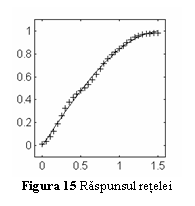
In fig. 14 este prezentata evolutia functiei de evaluare pentru cel mai bun cromozom, iar in fig. 15 raspunsul modul in care reteaua neuronala obtinuta aproximeaza functia f(x)=sin(x).
Controlul fuzzy al antrenarii
In paragraful 5 am vazut ca, prin modificarea parametrului ratei de antrenare, viteza de convergenta a algoritmului de antrenare cu propagarea inapoi a erorii creste. De asemenea, am vazut regulile care stau la baza modificarii parametrului h
Pentru cresterea semnificativa a performantei algoritmului de antrenare, pentru adaptarea valorii parametrului ratei de invatare poate fi utilizat un controler cu logica fuzzy (Anexa 2). Structura hibrida care realizeaza antrenarea este prezentata in fig. 14.
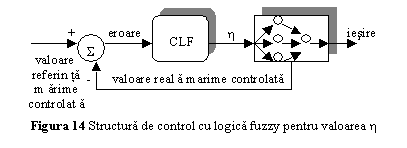
Controlerul cu
logica fuzzy utilizat in fig. 14 incorporeaza descrieri lingvistice in limbaj
natural ale valorilor parametrului ratei de invatare a algoritmului cu
propagarea inapoi a erorii. El contine 4 componente principale (fig. 15):
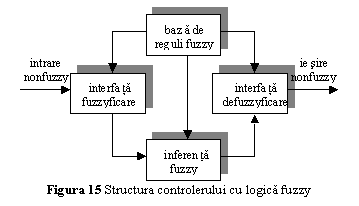
Interfata de fuzzyficare, care realizeaza urmatoarele actiuni:
o scalare a parametrilor de intrare, care modifica plaja de variatie a acestora in universul corespunzator al discursului;
fuzzyficarea datelor de intrare, care le transforma din marimi non-fuzzy, in valori lingvistice corespunzatoare, ce pot fi vazute ca etichete ale multimilor fuzzy;
Baza de reguli fuzzy, care reprezinta o multime de reguli de control lingvistice, scrise sub forma
"IF set de reguli satisfacute, THEN sunt inferate un set de consecinte"
Masina de inferenta fuzzy, care este o masina logica de decizii, utilizand baza de reguli fuzzy pentru a infera actiuni de control fuzzy, ca raspuns la valori fuzzy ale intrarii;
Interfata de defuzzificare , care furnizeaza o marime de iesire (de control) non-fuzzy, determinata dintr-o marime fuzzy.
Vom implementa un algoritm de antrenare cu moment si rata de invatare variabila, in care corectia ponderilor este data de relatia (35).
Pentru controlerul utilizat in acest exemplu, regula de defuzzificare folosita este regula centrului de greutate, in care interfata de defuzzyficare produce o marime non-fuzzy definita ca centrul de greutate al distributiilor posibilelor actiuni.
Ideea de baza a controlului fuzzy al algoritmului de antrenare cu propagarea inapoi a erorii, este implementarea unei euristici de forma unor reguli fuzzy "IF ., THEN .", care sa duca la o rata de convergenta sporita. Euristica implementata este bazata pe valoarea instantanee a erorii, definita de relatia (40). Conform acestei euristici, modificarea erorii (notata ME) este o aproximare a gradientului suprafetei de eroare, iar modificarea ME (notata MME) este o aproximare al gradientului de ordinul 2, asociat acceleratiei convergentei algoritmului de antrenare.
Regulile care guverneaza algoritmul de antrenare (Haykin, 1994) sunt :
IF ME is Small si nu apar schimbari de semn la iteratii consecutive ale algoritmului, THEN valoarea h creste;
IF apar schimbari de semn ale ME in iteratii consecutive ale algoritmului, THEN valoarea h trebuie scazuta, indiferent de valoarea MME;
IF ME is Small and MME is Small si nu sunt schimbari de semn pentru iteratii consecutive ale algoritmului, THEN valorile h si a trebuie crescute;
Primele doua reguli sunt similare presupunerilor 3 si 4 de la paragraful 5, iar regula 3, implicand modificarea valorii constantei momentului este noua.
Setul de date fuzzy utilizat pentru pentru determinarea h este dat in tabelul 1, iar pentru determinarea a in tabelul 2:
Tabelul 1: baza de reguli pentru modificarea parametrului h
|
ME |
|||||
|
MME |
NB |
NS |
ZE |
PS |
PB |
|
NB NS ZE PS PB |
NS NS ZE NS NS |
NS ZE PS ZE NS |
NS PS PS PS NS |
NS ZE PS ZE NS |
NS NS ZE NS NS |
Tabelul 2: baza de reguli pentru modificarea parametrului a
|
ME |
|||||
|
MME |
NB |
NS |
ZE |
PS |
PB |
|
NB NS ZE PS PB |
NS NS ZE ZE ZE |
NS ZE PS ZE ZE |
ZE ZE PS ZE ZE |
ZE ZE PS ZE NS |
ZE ZE ZE NS NS |
unde abrevierile utilizate au urmatoarele semnificatii: NB-Negative Big, NS-Negative Small, ZE-Zero, PS-Positive Small, PB-Positive Big.
Deci, setul de reguli lingvistice ce descriu variatia Dh a parametrului ratei de invatare pentru algoritmul de antrenare cu propagarea inapoi a erorii, vor fi de forma (exemplu):
IF ME is Negative Big and MME is Positive Small THEN Dh is Positive Small;
IF ME is Positive Small and MME is Zero THEN Dh is Positive Small;
Similar, setul de reguli lingvistice ce descriu variatia parametrului a al momentului, vor fi de forma
IF ME is Positive Small and MME is Zero THEN Da is Positive Small;
Considerand universul discursului pentru ME si MME ca fiind intervalul [-0.3, 0.3], functiile de apartenenta pentru ME si MME vor fi de forma prezentata in fig. 16.
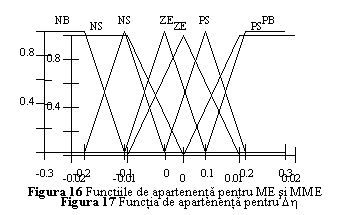
Considerand
universul discursului pentru Dh ca fiind [-0.02, 0.02] si urmarind tabelul 1,
din care rezulta ca Dh poate fi negativ mic, zero, sau pozitiv mic,
functia de apartenenta pentru modificarea parametrului ratei de invatare
rezulta ca in fig. 17.
Din testele facute in 1992 de Choi, rezulta o crestere semnificativa a algoritmului de antrenare cu propagarea inapoi a erorii, in cazul utilizarii controlului fuzzy, coroborata cu posibilitatea impunerii unei valori mult mai mici pentru eroarea acceptata, ca si conditie de stopare a algoritmului.
Reteaua neuronala Elman
Reteaua neuronala conectata inainte este o retea nerecurenta. Ea nu contine legaturi de reactie, nici in interiorul neuronilor ce o compun si nici la nivelul conexiunilor dintre acestia. Cu toate ca este la ora actuala poate cel mai des folosit tip de retea neuronala, exista aplicatii in care pot apare unele nejunsuri in utilizarea ei.
Un alt tip de retele neuronale, sunt retelele neuronale
recurente, care contin in structura lor conexiuni de reactie intre neuroni
apartinand aceluiasi strat sau unor straturi diferite. Printre acestea, reteaua
neuronala Elman este una din cele mai simple, putand fi antrenata cu ajutorul
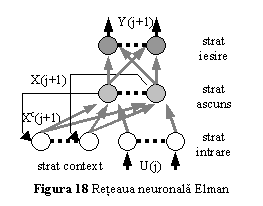
algoritmului standard cu propagarea inapoi a erorii . O retea Elman contine
patru straturi de neuroni (fig. 18).
Reteaua Elman este de fapt o retea conectata inainte cu un strat ascuns, neuronii acestuia avand uzual functii de activare liniara sau sigmoida, iar neuronii din stratul de iesire fiind liniari. In plus, reteaua contine un strat de context, avand aceeasi functie de activare ca si neuronii din stratul ascuns. Neuronii stratului de context sunt utilizati pentru a memora valoarea precedenta a iesirilor neuronilor din stratul ascuns.
Ponderile conexiunilor directe pot fi modificate in timpul antrenarii, dar ponderile conexiunilor de reactie sunt fixe.
Conform fig. 18, daca la momentul j este aplicat pe intrarea retelei vectorul U(j), aceasta va furniza la iesirea stratului de iesire vectorul Y(j ), iar vectorii de iesire ai stratului ascuns si de context sunt X(j+1) si respectiv Xc(j+1). Functionarea retelei va fi descrisa de ecuatiile
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
unde Wxc, Wxu si respectiv Wyx sunt matricile ponderilor legaturilor dintre stratul de context si stratul ascuns, stratul de intrare si stratul ascuns si respectiv stratul ascuns si stratul de iesire, iar j este o functie vectoriala liniara sau neliniara.
O concluzie interesanta se poate trage daca reteaua Elman contine doar neuroni cu functii de activare liniare. In acest caz, relatia (55) poate fi rescrisa ca
![]() (58)
(58)
Se observa ca relatiile (58) si (55) reprezinta descrierea standard in spatiul starilor a unui sistem dinamic. Ordinul acestuia depinde de numarul variabilelor de stare, care furnizeaza si numarul neuronilor din stratul ascuns.
Pentru simplitate, vom considera in determinarea relatiilor de modificare a ponderilor in timpul antrenarii, ca reteaua are un singur neuron de intrare si un singur neuron de iesire. In cursul antrenarii, retelei ii vor fi prezentate perechi de sabloane intrare/iesire de forma , j=1..N. Pentru sablonul j, eroarea patratica la iesire poate fi definita ca
![]() (59)
(59)
unde y(j) este iesirea reala a retelei, daca la intrare este aplicat semnalul u(j). Pentru intregul set de exemple de antrenare, eroarea patratica va fi
![]() (60)
(60)
Presupunand ca antrenarea se face in mod exemplu, ponderile retelei vor fi actualizate la fiecare iteratie j, respectand relatiile:
Wyx
![]() (61)
(61)
Wxu
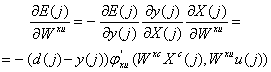 (62)
(62)
unde j xu este derivata functiei j in raport cu Wxu. Daca reteaua contine doar neuroni liniari, relatia (62) devine
![]() (63)
(63)
Wxc
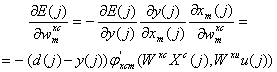 (64)
(64)
unde j xcm este derivata functiei j in raport cu wxcm, iar wxcm este elementul m al vectorului Wxc. Daca reteaua contine doar neuroni liniari, relatia (62) devine
![]() (65)
(65)
iar din (56) si (58) se poate scrie
![]() (66)
(66)
Conform algoritmului standard de antrenare cu propagarea inapoi a erorii, modificarea matricii (vectorului) ponderilor se face dupa relatia
![]() (67)
(67)
rezultand urmatorul algoritm de adaptare (in cazul linar)
![]() (68)
(68)
![]() (69)
(69)
![]() (70)
(70)
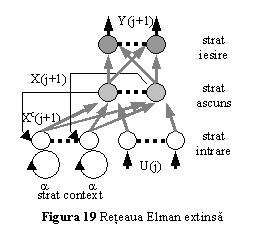
O varianta a retelei Elman se obtine prin adaugarea la nivelul neuronilor stratului de context, a unei conexiuni de autoreactie, ponderata prin intermediul unei valori fixe, subunitare a (fig. 19). In aceasta retea, iesirea neuronului m din stratul de context va fi data de relatia
![]() (71)
(71)
Dezvoltand relatia (72), se ajunge la
![]() (72)
(72)
adica iesirea unitatii m din stratul de context este obtinuta prin integrarea valorii iesirilor anterioare ale unitatii m din stratul ascuns, cu care aceasta este conectata. Cu cat valoarea constantei a este mai apropiata de unitate, cu atat pot fi luate in considerare mai multe valori anterioare ale iesirii neuronilor din stratul ascuns, deci cantitatea de informatie inmagazinata in retea creste.
Aplicand algoritmul de propagare inapoi a erorii pentru antrenarea retelei, se obtin relatiile de modificare a ponderilor:
![]() (73)
(73)
![]() (74)
(74)
![]() (75)
(75)
unde
![]() (76)
(76)
Se observa ca relatia (75) are aspectul unui raspuns infinit la impuls (IIR), ceea ce implica memorarea unei cantitati semnificativ crescute de informatie in reteaua Elman extinsa, comparativ cu reteaua Elman clasica.
Similar perceptronului multistrat, teorema 1 (Teorema aproximarii universale) este direct aplicabila retelei neuronale Elman si in consecinta si retelei neuronale Elman extinse. In concluzie si retelele neuronale Elman sunt aproximatori universali, putand fi teoretic antrenate sa aproximeze cu o eroare e orice functie continua, liniara sau neliniara, mono sau multivariabila.
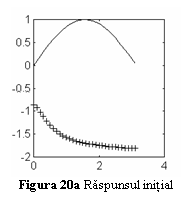
Spre exemplu, o retea neuronala
Elman, avand o unitate de intrare, un neuron liniar de iesire si trei neuroni
cu functii de activare sigmoida in stratul ascuns context va aproxima
functia f(x) sin(x)
in primul cadran ca in figurile urmatoare. Fig. 20a arata functia scop (linie
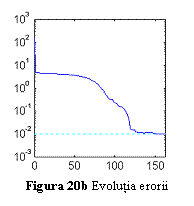
continua) si valorile initiale ale iesirilor retelei (marcate cu ). Fig. 20b arata evolutia erorii in cursul
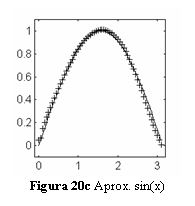
antrenarii, iar fig. 20c raspunsul retelei antrenate (marcat cu ) comparativ cu functia
scop (linie continua) la valori ale argumentului x diferite de cele la care au
fost prelevate esantioanele de antrenare. Eroarea
acceptata este de 0.01.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4157
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved