| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
TERMODINAMICA SOLUTIILOR (Neelectroliti
Acest capitol contine probleme de termodinamica solutiilor ideale si reale. Termochimia solutiilor s-a studiat in cap. XIII, iar termodinamica solutiilor de electroliti se va trata in vol. II.
1. Solutii ideale
O solutie ideala corespunde conditiei necesare si suficiente ca potentialul chimic al fiecarui component sa fie dat de expresii de forma:
![]() (XIX.1)
(XIX.1)
in care ![]() reprezinta potentialul
chimic standard (lichid pur) (v. cap. XIV). Presiunea de vapori a fiecarui
component este data de legea lui Raoult. Astfel, pentru solvent se scrie:
reprezinta potentialul
chimic standard (lichid pur) (v. cap. XIV). Presiunea de vapori a fiecarui
component este data de legea lui Raoult. Astfel, pentru solvent se scrie:
![]() (la fel si pentru fugacitati)
(la fel si pentru fugacitati)
sau
![]() (XIX.2)
(XIX.2)
in care ![]() este presiunea de
vapori a solventului pur, p1
este presiunea de vapori a solventului deasupra solutiei, iar xi este fractia moloara a
solventului in solutia care contine c componente.
este presiunea de
vapori a solventului pur, p1
este presiunea de vapori a solventului deasupra solutiei, iar xi este fractia moloara a
solventului in solutia care contine c componente.
Exemplul 1. Sa se arate ca, pentru o solutie binara:
![]() (ecuatia Duhem-Margules)
(ecuatia Duhem-Margules)
Rezolvare:
Potrivit ecuatiei
Gibbs-Duhem ![]() (v. cap. XIII) si
ecuatiei
(v. cap. XIII) si
ecuatiei ![]() , se poate scrie:
, se poate scrie:
![]()
Conform ecuatiilor (XIX.1) si (XIX.2) se obtine:


Rezulta, astfel:
![]() si
si ![]()
(la o presiune totala si temperatura constante).
Ecuatia Duhen-Margules este valabila pentru solutiile reale si ideale. Ea reprezinta un criteriu de verificare a ecuatiilor propuse pentru proprietatile termodinamice ale solutiilor.
Solutiile ideale reprezinta cea mai simpla stare de comparatie a solutiilor reale. In unele cazuri, asemanarea dintre solutiile ideale si reale este foarte mare, de exemplu, in cazul speciilor moleculare similare, ca izotopii, sau clorbenzen + brom-benzen, hexan + heptan, etc.
Pentru echilibrul solutie (componente 1 + 2) - vapori (component 1) se poate scrie ecuatia:
![]() (XIX.3)
(XIX.3)
La presiune constanta variatia temperaturii de fierbere cu compozitia este data de ecuatia:
![]() sau
sau ![]() (la p = const)
(la p = const)
Se obtine:
![]()
si prin integrare
intre ![]() , temperatura de fierbere a solventului pur (x1 = 1) si temperatura de
fierbere pentru compozitia solutiei (x1),
rezulta:
, temperatura de fierbere a solventului pur (x1 = 1) si temperatura de
fierbere pentru compozitia solutiei (x1),
rezulta:
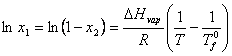 (XIX.4)
(XIX.4)
In mod asemanator, pentru echilibrul solutie (componente 1 + 2) - cristale (component 1), se poate scrie:
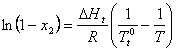 (XIX.5)
(XIX.5)
Pentru echilibrul osmotic solvent (component 1) - membrana (permeabila pentru componentul 1) - solutie (componente 1 + 2):
μ1 (lichid pur) = μ1 (solutie)
deorece presiunile sunt diferite, rezulta:
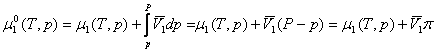
(neglijand
compresibilitatea izoterma a lichidului), in care ![]() (presiunea deasupra
solutiei - presiunea deasupra solventului pur) reprezinta presiunea osmotica,
iar
(presiunea deasupra
solutiei - presiunea deasupra solventului pur) reprezinta presiunea osmotica,
iar ![]() este volumul partial molar al solventului. Se
obtine, astfel:
este volumul partial molar al solventului. Se
obtine, astfel:
![]() (XIX.6)
(XIX.6)
Ecuatiile
stabilite (XIX.3 - XIX.6) sunt valabile si pentru solutii cu mai multe
componente, cu ![]() pentru speciile
dizolvate.
pentru speciile
dizolvate.
Pentru
solutiile ideale diluate, x2
<< 1, ![]() si ln (1 - x2)
si ln (1 - x2) ![]() -x2 (prin aplicarea teoremei lui Mac Laurin si neglijarea
termenilor superiori), iar
-x2 (prin aplicarea teoremei lui Mac Laurin si neglijarea
termenilor superiori), iar ![]() . Astfel ecuatiile (XIX.4 - XIX.6) devin:
. Astfel ecuatiile (XIX.4 - XIX.6) devin:
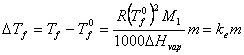 (variatia ebuliometrica) (XIX.7)
(variatia ebuliometrica) (XIX.7)
 (variatia criometrica) (XIX.8)
(variatia criometrica) (XIX.8)
![]() (presiunea osmotica) (XIX.9)
(presiunea osmotica) (XIX.9)
ke si kc
sunt constantele molale, m este
molalitatea solutiei si c este
concentratia in mol ∙ l-1, ![]() si
si ![]() reprezinta temperatura
de fierbere, respective de topire, a solventului pur, iar
reprezinta temperatura
de fierbere, respective de topire, a solventului pur, iar ![]() este volumul molecular
al solventului pur.
este volumul molecular
al solventului pur.
Exemplul 2. O solutie cu 0,6308 g acetanilida la 26,35 g alcool etilic fierbe la o temperatura cu 0,204 C mai ridicata decat solventul pur. Sa se calculeze caldura de vaporizare a alcoolului etilic la temperature de fierbere (78 C).
Rezolvare:
Cresterea molala a temperaturii de fierbere corespunde la 135 g acetanilida dizolvata in 1000 g alcool, deci (v. ecuatia (XIX.7)):
![]()
si

Exemplul 3. O proba de sulf rombic incepe sa se topeasca la 119,25 C, dar, in cateva minute, temperatura de topire scade la 114,5 C. Daca topitura intregii cantitati de sulf se raceste brusc, 3,6% din sulful solid obtinut este insolubil in sulfura de carbon.
Sa se interpreteze rezultatele si sa se deduca formula moleculara a sulfului insolubil in sulfura de carbon.
Rezolvare:
Constanta criometrica a sulfului este (din ecuatia (XIX.8)):
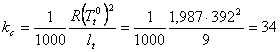
Din aceeasi ecuatie:
![]()
se obtine M = 268. Formula probabila a sulfului insolubil (sulf monociclic) este S8.
Exemplul 4. Depresiunea crioscopica a unei solutii care contine 5,5 g NaNO3 la 76,2 g apa este de 2,852 C. Sa se calculeze masa moleculara aparenta a dizolvatului si gradul aparent de disociere.
R e z o l v a r e:
Conform
relatiei (XIX.8) ![]() (m1 si m2 fiind masa dizolvatului, respectiv a
solventului) se obtine masa moleculara aparenta Ma:
(m1 si m2 fiind masa dizolvatului, respectiv a
solventului) se obtine masa moleculara aparenta Ma:
![]()
Valoarea calculata a masei moleculare este 85.
Se
observa ca, pentru o anumita solutie, proprietatile coligative (scaderea
presiunii de vapori, depresiunea criometrica, etc.) sunt invers proportionale
cu masa moleculara, de exemplu, ![]() .
.
Notand cu indicii calc valorile calculate si cu indicii exp valorile experimentale, se obtine:
![]() si
si ![]()
Pe de alta parte, notand cu i factorul lui van't Hoff (numarul total de moli si de ioni-g din solutie) pentru un electrolit care da ν ioni prin disociere, pentru un mol electrolit se obtine:
![]()
In cazul NaNO3 ν = 2 si i = 1 + α, α fiind gradul de disociere aparent in solutie.
Intre
![]() si
si ![]() se poate stabili
relatia:
se poate stabili
relatia:
![]()
deoarece ![]() si
si ![]() (m fiind molalitatea).
(m fiind molalitatea).
Potrivit relatiei scrise mai sus:
![]()
de unde
![]()
Pentru NaNO3 se obtine: 47,1(1 + α) = 85, de unde α = 0,805 sau 80,5%.
Exemplul 5. Sa se calculeze presiunea de vapori la 100 C a unei solutii care contine 5,61 g Na2SO4 la 100 g apa, considerand sarea disociata 85%.
Rezolvare:
Ecuatia
(XIX.2) ![]() conduce la:
conduce la:
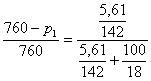
de unde 760 - p1 = 5,40 mm col. Hg.
Deoarece Na2SO4 se disociaza 85%, factorul lui van't Hoff i este 1 + 2α = 2,7 pentru ca ν = 3 potrivit ecuatiei:
![]()
Scaderea observata a presiunii va fi: 5,40 ∙ 2,7 = 14,6 mm col. Hg si presiunea de vapori a solutiei va fi: 760 - 14,6 = 745,4 mm col. Hg.
Exemplul 6. Se dizolva 0,5 g acid acetic in 20 g benzen: depresiunea crioscopica este 1,04 C.
Sa se analizeze constitutia acidului acetic in benzen.
Rezolvare:
Constanta criometrica a benzenului este kc = 5,07.
Masa moleculara aparenta a acidului acetic este:
![]()
Acidul acetic este format in benzen numai din molecule duble (CH3COOH)2.
Considerand
reactia de asociere 2A ↔ A2, factorul lui van't Hoff este i = ![]() , α fiind gradul de asociere la molecule duble.
, α fiind gradul de asociere la molecule duble.
Valoarea
ΔTcalc este -2,08 C
si, deoarece ![]() =
= ![]() , rezulta:
, rezulta:
![]() si α = 1 sau 100%
si α = 1 sau 100%
In general, o asociere de tipul nA ↔ (A)n conduce la:
![]()
Exemplul 7. Se agita 100 ml lichid organic A avand densitatea 0,92 g ml si masa moleculara 46, cu 100 ml apa. Lichidul A este relativ putin solubil in apa. Temperatura de cristalizare a apei in solutia saturata este -2,65 C.
In lichidul A se adauga 5 g substanta organica solubila in A, dar insolubila in apa si, dupa dizolvare, solutia apoasa are o temperatura de cristalizare de -2,32 C.
Sa se calculeze masa moleculara a substantei dizolvate in A.
Rezolvare:
Considerand
solutiile ideale, la echilibrul substanta A pura (faza α) - solutie
saturata (faza β), deoarece ![]() , rezulta:
, rezulta:
![]()
![]() fiind fractia molara
de saturatie in apa, in absenta substantei straine, iar pentru echilibrul
solutie A (cu dizolvat) - solutie saturata:
fiind fractia molara
de saturatie in apa, in absenta substantei straine, iar pentru echilibrul
solutie A (cu dizolvat) - solutie saturata:
![]()
![]() fiind fractia molara a
substantei A in solutia cu substanta straina si
fiind fractia molara a
substantei A in solutia cu substanta straina si ![]() , fractia molara de saturatie in apa. Se obtine, astfel:
, fractia molara de saturatie in apa. Se obtine, astfel:
![]()
Conform
ecuatiei ![]() (ecuatia (XIX.8)):
(ecuatia (XIX.8)):
![]() ,
,
m fiind molalitatea, iar indicii respectivi arata solutiile.
Fractia molara a substantei dizolvate in lichidul A este x = 0,12 si masa moleculara M = 20.
Exemplul 8. Sa se stabileasca ecuatia variatiei temperaturii de cristalizare a unei solutii, la separarea din lichid a unei solutii solide. Se va considera cazul solutiilor ideale.
Rezolvare:
La echilibru, pentru fiecare component se poate scrie:
![]() sau
sau ![]()
Pentru solvent:
![]()
in care z1 si x1 reprezinta fractia molara a solventului in solutia solida, respectiv lichida la echilibru.
La p = const, se obtine:

si, prin integrare
intre limitele z1 = x1 = 1 si z1, x1, respectiv ![]() si T:
si T:

sau, cu transformarea obisnuita (ca la obtinerea ecuatiilor (XIX.7 - XIX.9)):
![]()
Rezulta:
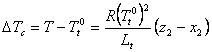
Introducand
coeficientul de distributie ![]() , se obtine:
, se obtine:
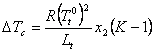 si
si ![]()
Daca K > 1, temperatura de cristalizare a solutiei solide este mai mare decat a solventului pur.
Pentru
K = 0 (solid pur, z1 = 1) ecuatia capata forma
cunoscuta ![]() .
.
Exemplul 9. Presiunea de vapori apei la 16 C este 13,624 mm col. Hg, iar presiunea de vapori a solutiei de glucoza este 13,588 mm col. Hg. Sa se calculeze presiunea osmotica a solutiei de glucoza la 16 C.
Rezolvare:
Din
![]() (v. ecuatiile (XIX.2)
si (XIX.6)) si facand inlocuirea
(v. ecuatiile (XIX.2)
si (XIX.6)) si facand inlocuirea ![]() , se obtine:
, se obtine:

Pentru a exprima
π in cm. col. Hg, se inlocuieste  . Astfel, rezulta π = 254 cm. col. Hg.
. Astfel, rezulta π = 254 cm. col. Hg.
Exemplul 10. Presiunea osmotica a unei solutii de 4 g policlorura de vinil la 1 l dioxan este de 6,4 ∙ 10-4 atm la 27 C. Sa se calculeze masa moleculara aproximativa a polimerului.
Rezolvare:
Conform ecuatiei presiunii osmotice (XIX.9) π = cRT, in care c este concentratia molara (mol ∙ l-1), se obtine:
![]() , de unde
, de unde ![]()
Observatie: In solutiile de polimeri exista o anumita distributie a polimerului. Notand cu Ni numarul de macromolecule cu masa moleculara Mi, masa moleculara medie in raport cu numarul de molecule, determinata prin metoda presiunii osmotice, este:

deosebita de valoarea obtinuta prin metoda vascozitatii (v. cap. VIII).
Exemplul 11. Sa se arate ca presiunea osmotica a unei solutii de concentratie c este data de ecuatia:
![]()
in care π este presiunea osmotica, M este masa moleculara a solventului, ρ este densitatea (g ∙ ml-1)
solutiei, c este concentratia
solutiei, in mol ∙ l-1, ![]() este presiunea de
vapori a solventului pur la temperatura T
si p1 este presiunea de
vapori a solutiei la temperatura T.
este presiunea de
vapori a solventului pur la temperatura T
si p1 este presiunea de
vapori a solutiei la temperatura T.
Rezolvare:
Daca solutia contine n1 moli solvent cu masa moleculara M1 si 1 mol dizolvat cu greutatea moleculara M2 in V litri, densitatea ρ este data de ecuatia:
![]()
![]()
si
![]()

Deoarece c este concentratia solutiei in mol
∙ l-1 ![]() , se obtine:
, se obtine:

sau
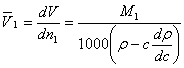
Rezolvare:
Rezolvare:
Rezolvare:
Rezolvare:
Rezolvare:
|
| |||
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1338
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved