Mecanica clasica

Mecanica clasica

Mecanica clasica se bazeaza pe legi ale naturii ce au fost formulate de Isaac Newton in anul 1686 in lucrarea sa, devenita celebra, 'Principiile fundamentale ale stiintelor naturii'. Mai precis, mecanica este acea parte a fizicii care studiaza miscarea mecanica a corpurilor si conditiile de echilibru ale acestora. Problema mecanicii este stabilirea ecuatiilor de miscare ale corpurilor.

Ecuatiile de miscare dau forma traiectoriei micarii corpului. Traiectoria indica pozitiile succesive in spatiu pe care le va ocupa corpul de-a lungul miscarii sale.

Notiumi generale

Cunoaterea miscarii unui corp presupune stabilirea localizarii lui in spatiu si in timp. Fie un punct material M, aflat in micare pe o traiectorie in spatiu, ca in fig.1.

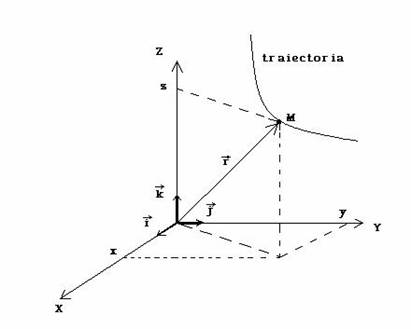
Fig. 1. Traiectoria punctului material intr-un sistem de referinta cartezian.

Pozitia unei particule la orice moment de timp t este specificata de vectorul de pozitie a carui expresie reprezinta legea de miscare:

Prin eliminarea timpului din ecuatiile parametrice ale traiectoriei x=x(t), y=y(t), z=z(t) se obtin ecuatiile traiectoriei.

Vectorul viteza momentana este derivata vectorului de pozitie in raport cu timpul, iar prin derivarea legii de miscare se obtine legea vitezei:

.

Vectorul acceleratie momentana este derivata intai a vectorului viteza in raport cu timpul, sau derivata a doua a vectorului de pozitie in raport cu timpul:

.

Impulsul este: .

Principiul fundamental al mecanicii ;

Pentru masa constanta, principiul fundamental al mecanicii se scrie: .

Legea de miscare, legea vitezei, acceleratia ca functii de timp, ecuatiile traiectoriei descriu, ceea ce se numeste, miscarea unui mobil. Aceste relatii nu sunt independente. Cunoscandu-se conditiile initiale (pozitia si viteza la momentul initial), prin calcule matematice se obtine una din aceste legi din alta, adica se cunoaste miscarea mobilului.

Cunoscand legea de miscare a unui corp , prin operatia de derivare se afla legea vitezei , iar apoi derivand legea vitezei se afla acceleratia ca functie de timp , respectiv forta ce actioneaza asupra corpului daca acesta are masa con

. Vectorul viteza momentana este tangent la traiectorie, aa cum se vede in fig.

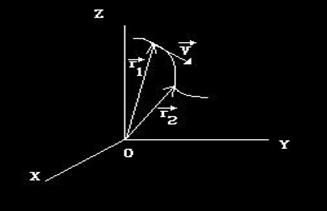
Fig. Vectorul viteza momentana.

Din legea de miscare eliminand timpul se pot scrie ecuatiile explicite ale traiectoriei.

Aflati viteza si acceleratia punctelor materiale descrise de urmatorii vectori de pozitie:

a)    (m);

b)   (m);

c)    (m);

d)   (m).

Ecuatiile miscarii unui mobil sunt urmatoarele:

x = r cos ωt m), y = r sin ωt (m), z = t (m), unde r, ω, sunt constante pozitive. Sa se afle:

a)    vectorul viteza, modulul vitezei;

b)   vectorul acceleratie, modulul acceleratiei.

R: a) m/s; b) m/s

O particula de masa m se misca dupa legea:

x = α cos ωt m), y = β sin ωt (m), unde α, β, ω sunt constante pozitive.

a)    Precizati unitatile de masura ale constantelor α, β si ω;

b)   Determinati forta care actioneaza asupra particulei in functie de pozitia particulei.

R:

Miscarea unui punct material in planul xOy este descrisa de legea:

x = α sin ωt m), y = α (1 - cos ωt) (m), unde α si ω sunt constante pozitive. Determinati unghiul dintre vectorul viteza si vectorul acceleratie al punctului material.

R:

Din legea de miscare eliminand timpul se pot scrie ecuatiile explicite ale traiectoriei.

Vectorul de pozitie al unui punct material A variaza dupa legea:

(m), unde α, β sunt constante pozitive. Determinati:

a)    ecuatia traiectoriei punctului; reprezentati grafic;

b)   vectorii viteza si acceleratie si modulele acestora;

c)    unghiul θ intre vectorii acceleratie si viteza in functie de timp.

Rezolvare:

a) - ecuatia traiectoriei;

Traiectoria este o parabola cu varful V(0,0), iar punctul A se misca pe jumatate din aceasta parabola ( x0).

b) , vectorul viteza este tangent la traiectorie in fiecare punct al acesteia;

, in acest caz vectorul acceleratie este paralel cu directia axei Oy si in sens opus acesteia in fiecare punct al traiectoriei;

c) Unghiul pe care vectorul viteza il face cu axa Oy este (π - θ),

sau daca se calculeaza cu ajutorul produsului scalar dintre vectorii si :

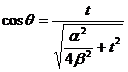
Miscarea unei particule in plan este descrisa de legea:

x = β t m), y = α t (1- β t) (m), unde α, β sunt constante pozitive. Determinati:

a)    ecuatia traiectoriei particulei; reprezentati grafic;

b)   vectorii viteza si acceleratie si modulele acestora;

c)    momentul t₀ la care vectorul viteza face un unghi de π/4 cu vectorul acceleratie.

R: a) ; c).

Sa se scrie ecuatia traiectoriei, precizand forma acesteia pentru particula care se misca dupa legea:

a)    problemei 5;

b)   problemei

Doua particule se deplaseaza cu vitezele m/s, respectiv m/s. La momentul t₀=0 particulele se gasesc in pozitiile m, respectiv m. Sa se determine momentul la care distanta dintre particule este minima.

R: t = 0,6 s.

Doua particule se deplaseaza cu vitezele m/s, respectiv m/s. La momentul t₀ =0 particulele se gasesc in pozitiile m, respectiv m. Sa se determine momentul la care distanta dintre particule este minima.

Rezolvare:

,

, ,

,

;

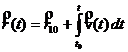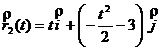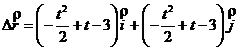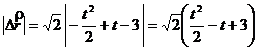si

t=1 s.

Operatia inversa derivarii fiind integrarea, din legea vitezei se obtine prin integrare legea de miscare . Cunoscandu-se acceleratia (sau forta) ca functie de viteza (de obicei fortele rezistente depind de viteza), prin integrare se poate afla legea vitezei si, mai departe, printr-o noua integrare, se poate descrie miscarea prin legea de miscare .

Un corp de masa m porneste la momentul t₀ = 0 de la x₀ = 0 cu viteza v₀ intr-un mediu viscos de-a lungul axei Ox. Corpul intampina din partea mediului o forta de rezistenta proportionala cu viteza (F = - α v). Sa se determine:

a)    legea vitezei;

b)   legea de miscare;

c)    dupa cat timp viteza initiala a corpului, v₀, se micsoreaza de n ori.

Rezolvare:

a)

;

b) ;

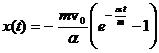c) Se inlocuieste v cu in legea vitezei si se obtine .

Un corp de masa m intampina, din partea mediului in care se misca de-a lungul axei Ox, o forta de rezistenta proportionala cu patratul vitezei; constanta de proportionalitate este α (F = - α v²). Presupunand ca la momentul t₀ = 0 corpul se gaseste la x₀ = 0 si are viteza v₀ sa se determine:

a)    legea vitezei;

b)   legea de miscare;

c)    dupa cat timp viteza initiala a corpului, v₀, se micsoreaza de n ori.

R: a) 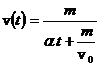; b) ; c) .

Un corp de masa m, care se misca in lungul axei Ox, intampina din partea mediului in care se misca o forta de rezistenta proportionala cu cubul vitezei (F = - α v³). Presupunand ca la momentul t₀ = 0 corpul pleaca de la x₀=0 si are viteza v₀ si neglijand restul interactiunilor, sa se determine:

a)    legea vitezei;

b)   legea de miscare;

c)    dupa cat timp viteza initiala a corpului, v₀, se micsoreaza de n ori.

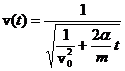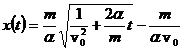R: a); b); c) .

O particula se misca incetinit in sensul pozitiv al axei Ox cu acceleratia , unde α constanta pozitiva. Stiind ca la momentul t₀ = 0, x₀ = 0, iar viteza este v₀, determinati:

a)    legea vitezei;

b)   legea de miscare;

c)    drumul parcurs pana la oprire si intervalul de timp corespunzator.

R: a) ; b) ;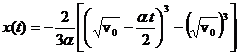

c) , .

Cunoscandu-se viteza ca functie de pozitie , prin integrare se poate afla legea de miscare si, mai departe, se poate descrie miscarea prin legea dorita, folosind operatiile matematice amintite mai sus.

O particula se deplaseaza in planul xOy cu viteza , unde α, β sunt constante. La momentul initial t₀ = 0 particula se gaseste in punctul x₀ = y₀ = 0. Determinati:

a)    legea de miscare;

b)   legea vitezei;

c)    ecuatia traiectoriei;

d)   acceleratia

R: a) .

O particula de masa m se deplaseaza in sensul pozitiv al axei Ox cu o viteza , unde α constanta pozitiva. Stiind ca la momentul t₀ = 0 particula se gaseste in punctul x₀ = 0 determinati:

a)    legea de miscare;

b)   legea vitezei;

c)    acceleratia;

d)   lucrul mecanic al tuturor fortelor ce actioneaza asupra particulei in primele t secunde ale miscarii.

R: a) ; d) .

Aceeasi problema pentru .

R: a) ; d).

Atunci cand se cunosc ecuatiile traiectoriei, prin derivari succesive ale acestora, si folosind conditiile initiale se poate deduce acceleratia ca functie de pozitie .

O particula de masa m se misca pe traiectoria cu o

acceleratie paralela cu axa Oy. La t₀ = 0 particula se gaseste in punctul de coordonate x₀ = 0, y₀ = b si are viteza v₀. Determinati forta care actioneaza asupra particulei in fiecare punct al traiectoriei.

Rezolvare:

- ecuatia traiectoriei;

Derivand ecuatia traiectoriei in raport cu timpul se obtine:

sau

Conditiile initiale:

t₀ = 0, x₀ = 0, y₀ = b, v₀ ,

a_y a_x = 0 v_x = const.

se inlocuiesc in (1) si

v_0y = 0 si deci v_0x = v₀ v_x = const = v₀

Derivand (1) inca o data in raport cu timpul si utilizand, din nou, conditiile initiale, se obtine:

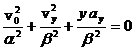
Inlocuind v_y din (1) si folosind ecuatia traiectoriei se obtine:

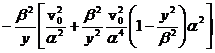
a_y = a_y =

Astfel  F_y , iar .

O particula se deplaseaza pe o traiectorie plana cu viteza constanta in modul (v). Determinati acceleratia particulei in punctul x₀ = 0 pentru o traiectorie descrisa de ecuatia:

a)   

b)  

Rezolvare:

a) v_y = 2α x v_x (1)

Dar v_x²+ v_y² = v² = const. v_x² +4 α²x² ) = v² (2)

;

a_y = 2 α v_x²+2 α x a_{x ;}

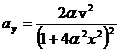Pentru x₀ = 0 y₀ =0 ;

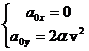b) R: .

Un corp de masa m se afla in repaus pe un plan orizontal. La momentul t₀ = 0 asupra lui incepe sa actioneze o forta data de legea F = α t, unde α este o constanta. Forta face un unghi θ cu orizontala. Neglijind frecarea sa se determine:

a) legea vitezei, pana la parasirea planului orizontal;

b) viteza v₁ a corpului in momentul in care acesta paraseste planul;

c) legea de miscare, pana la parasirea planului;

d) drumul parcurs de corp din momentul initial pana la parasirea planului.

Rezolvare:

a) Pana la parasirea planului orizontal acceleratia corpului este:

F cos θ = m a ,

;

b) In momentul desprinderii componenta verticala a fortei este egala cu greutatea, astfel incat:

F sin θ =G α t₁ sin θ = mg ,

;

c) R: ; d) R: .

Un corp de masa m se afla in repaus pe un plan orizontal. La momentul t₀ = 0 asupra lui incepe sa actioneze o forta data de legea F = , unde α este o constanta. Forta face un unghi θ cu orizontala. Neglijind frecarea, sa se determine:

a)    viteza v₁ a corpului in momentul in care acesta paraseste planul;

b)   drumul parcurs de corp din momentul initial pana la parasirea planului.

R: a) ; b) .

Principiile fundamentale ale dinamicii

Rezolvarea problemelor de mecanica clasica se bazeaza pe cateva principii fundamentale, obtinute prin generalizarea observatiilor experimentale. Cele trei principii, ce au fost formulate de Galilei si de Newton, sunt suficiente pentru a explica toate miscarile mecanice clasice, adica miscarile ce se desfasoara cu viteze mult mai mici decat viteza luminii in vid, c = 3 1 ⁸ m/s. Daca vitezele punctelor materiale se apropie de viteza luminii in vid, atunci micarile lor se supun principiilor relativitatii restranse ale lui Einstein.

Principiul inertiei

Principiul inertiei a fost formulat prima data de Galilei si este cunoscut sub forma urmatoare:

'Un corp ii pastreaza starea de repaus sau de micare rectilinie si uniforma atata timp cat asuprea lui nu se exercita nici o forta, sau daca rezultanta tuturor fortelor este zero'.

Principiul inertiei introduce notiunea de forta. Forta este o marime vectoriala, avand ca unitate de masura in SI 1 newton, [F _SI = 1 N Prin intermediul fortelor, corpurile actioneaza unele asupra altora transmitand micarea mecanica. Campurile de forte sunt si ele raspunzatoare de transmiterea interactiunilor mecanice.

Conform acestui principiu, rezultanta egala cu zero a unui numar oarecare de forte este echivalenta cu inexistenta fortei. Miscarea unui corp asupra caruia actioneaza mai multe forte a caror rezultanta este nula sau asupra caruia nu actioneaza nici o forta se numeste micare inertiala.

Asa cum stim, micarea este caracterizata in raport cu un sistem de referinta ales arbitrar, de aceea micarea are caracter relativ. In acest sens, Galilei a formulat principiul relativitatii miscarii mecanice. Sa consideram un calator aezat intr-un vagon de tren, ce se deplaseaza rectiliniu si uniform. Calatorul se poate gasi intr-una din starile mecanice urmatoare: (i) este in repaus, in raport cu sistemul de referinta legat de tren, (ii) este in miscare rectilinie uniforma cu o viteza egala cu viteza trenului fata de un sistem de referinta legat de Pamant, (iii) este in miscare accelerata, in raport cu un sistem de referinta legat de Soare, deoarece Pamantul este in micare accelerata fata de Soare. Toate sistemele de referinta ce se misca rectiliniu si uniform se numesc sisteme de referinta inertiale. In aceste sisteme de referinta este valabil principiul inertiei.

Principiul fortei sau a doua lege a dinamicii

Newton a descoperit faptul ca o forta care actioneaza asupra unui corp ii imprima acestuia o acceleratie, proportionala cu forta si invers proportionala cu masa corpului.

Derivata impulsului al unui punct material in raport cu timpul , reprezinta rezultanta F a fortelor care actioneaza asupra punctului vectorial ca urmare a interactiunilor cu alte corpuri. Forta este direct proportionala cu produsul dintre masa si acceleratia corpului.

sau

constanta de integrare

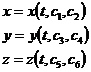
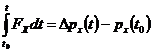aria suprafetei masurate este egala cu variatia componentei impulsului pe axa O_x t= t- t₀

Masa este o masura a cantitatii de materie continuta in corp. Cantitatea de micare sau impulsul unui corp se definete ca produsul dintre masa si vectorul viteza al corpului:

Unitatea de masura pentru impulsul mecanic este [p]_SI =1 kg m s^-1.

Principiul actiunii si reactiunii

' Oricarei actiuni i se opune intotdeauna o reactiune egala in modul si de sens contrar.' Cele doua forte, actiunea si reactiunea, sunt aplicate simultan si la corpuri diferite, de-a lungul dreptei care unete cele doua corpuri. In acest caz este vorba de interactiunea mutuala simultana si nu de o cauza si un efect.

Principiul independentei actiunii fortelor

Experimental, se constata ca fiecare dintre fortele la care este supus un corp actioneaza independent de celelalte forte aplicate corpului. Din acest principiu rezulta posibilitatea inlocuirii unui ansamblu de forte, F₁ , F₂ , , F_n , prin rezultanta lor, egala cu suma vectoriala a acestora.

Principiul relativitatii din mecanica clasica

Micarea mecanica este raportata la sisteme de referinta. Din acest punct de vedere, micarea este relativa. Sistemele de referinta pot fi in repaus, in micare rectilinie si uniforma (sisteme de referinta inertiale), sau in micare accelerata (sisteme de referinta neinertiale). In anul 1632 Galilei enunta principiul relativitatii in mecanica clasica, afirmand ca toate legile mecanicii raman neschimbate fata de orice sistem de referinta inertial. Din punct de vedere mecanic, toate sistemele de referinta inertiale sunt absolut echivalente. Nici un sistem de referinta inertial nu poate fi considerat absolut, toate fiind egal indreptatite. Prin urmare, nici o experienta mecanica efectuata in interiorul unui sistem de referinta inertial nu ne permite sa determinam miscarea rectilinie si uniforma sau starea de repaus a sistemului de referinta fata de stelele fixe (adica fata de alte sisteme de referinta inertiale). Din interiorul vagonului de tren din exemplul anterior nu ne putem da seama daca acesta merge uniform si rectiliniu sau sta pe loc, deoarece orice experienta mecanica da acelai rezultat in ambele cazuri.Lucrurile se schimba radical atunci cand avem de-a face cu sisteme de referinta neinertiale, adica aflate in micare accelerata. In acest caz legile lui Newton nu mai sunt valabile si cu ajutorul experientelor mecanice efectuate in interiorul sistemului putem determina acceleratia acestuia. In sistemele de referinta neinertiale se excercita fortele de inertie. Cel mai simplu exemplu de forta de inertie este forta centrifuga din micarea circulara.

3 Teoreme generale in dinamica punctului material

Ca o consecinta a principiilor fundamentale ale dinamicii, se obtin legile ce guverneaza unele marimi fizice ale punctului material (impuls mecanic, energie, moment cinetic). Aceste legi se mai numesc si teoremele generale in dinamica punctului material.

Energia

Lucrul mecanic elementar, respectiv lucrul mecanic total la trecerea din starea 1 in starea 2 sunt:

.

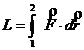Observatie: đL reprezinta lucrul mecanic elementar si nu diferentiala lucrului mecanic.

Daca forta este constanta pe tot parcursul deplasarii .

- puterea mecanica; .

đL = dE_c - teorema variatiei energiei cinetice;

Lucrul mecanic al fortelor care deriva din potential este: đL= - dU, iar fortele campului potential se exprima:

= - grad U,

unde U = U( x, y, z ) - potentialul sau energia potentiala este functie de pozitie;

- operatorul nabla.

E = E_c + U - energia totala.

Fortele constante (N) si (N) actioneaza simultan asupra unei particule in timpul deplasarii acesteia din punctul A(4, 7, 5) (m) in punctul B(9, 0, 8) (m). Care este lucrul mecanic efectuat asupra particulei?

R: 30 J

O particula se deplaseaza pe o traiectorie in planul xOy din punctul de vector de pozitie m, in punctul de vector de pozitie m. Ea se deplaseaza sub actiunea unei forte N. Calculati lucrul mecanic efectuat de forta .

R: - 40 J.

Un corp de masa m = 4 kg se misca dupa legea m. Sa se calculeze lucrul mecanic efectuat asupra corpului in intervalul de timp t₀ = 0, t₁ = 2 s.

Rezolvare:

,

, ;

;

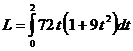
J.

Un corp de masa m = 1 kg se misca dupa legea m. Sa se calculeze lucrul mecanic efectuat asupra corpului in intervalul de timp t₀ = 0, t₁ = 1 s.

R: L = 20 J.

Asupra unui corp de masa m aflat pe un plan orizontal actioneaza o forta constanta in modul F = mg/ Pe parcursul deplasarii forta face cu orizontala un unghi care variaza dupa legea θ = α x, unde α este o constanta, iar x este drumul parcurs (x₀ = 0). Sa se calculeze viteza v₁ a corpului in momentul in care unghiul θ = π/

Rezolvare:

F sin θ < G , pentru orice x pe tot parcursul deplasarii corpul ramane pe planul orizontal;

Lucrul mecanic, al fortelor care actioneaza asupra corpului, se reduce la lucrul mecanic al componentei fortei de-a lungul planului orizontal :

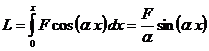
Folosind teorema variatiei energiei cinetice:

L = ∆E_c .

Daca se cunoaste forta, sau acceleratia, ca functii de pozitie, legea vitezei

se poate obtine folosind teorema variatiei energiei cinetice si definitia lucrului mecanic, iar legea de miscare rezulta prin integrarea legii vitezei. O alta modalitate de a obtine legea de miscare este rezolvarea ecuatiei diferentiale la care conduce principiul fundamental al mecanicii.

Un corp de masa m se misca in lungul axei Ox sub actiunea unei forte care variaza dupa legea F = α x, unde α este o constanta pozitiva. Stiind ca, la momentul t₀ = 0, corpul se gaseste in x₀ si are viteza v₀ = 0, sa se determine:

a)    legea de miscare;

b)    legea vitezei.

R: a) ; b) .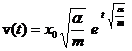

Un corp de masa m se misca in lungul axei Ox sub actiunea unei forte care variaza dupa legea F = α x, unde α este o constanta pozitiva. Stiind ca, la momentul t₀ = 0, corpul se gaseste in x₀ = 0 si are viteza v₀ , sa se determine:

a)    legea de miscare;

b)    legea vitezei.

Rezolvare:

a) Folosind teorema variatiei energiei cinetice: L = ∆E_c si definitia lucrului mecanic: ,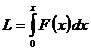

se obtine lucrul mecanic si deci ;

Prin integrare se obtine legea de miscare implicita:

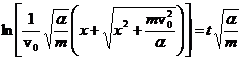
care, prin cateva artificii matematice duce la legea de miscare explicita.

Daca se abordeaza problema rezolvand ecuatia diferentiala ce rezulta in urma aplicarii principiului fundamental al mecanicii:

atunci legea de miscare rezulta in mod explicit si este:

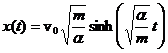
b) R: .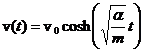

Un corp de masa m este ridicat de la suprafata Pamantului cu ajutorul unei forte care depinde de altitudinea y dupa legea , unde α este o constanta pozitiva. Calculati lucrul mecanic al acestei forte si variatia energiei potentiale a corpului pe portiunea y = 0, y = 1/2α.

R: ; .

Un resort special are legea fortei F = - α x³. Care este energia potentiala in punctul x, presupunand E_p = 0 la x₀ = 0.

R: E_p = α x⁴ / 4.

Stiind ca potentialul fortei este dat de expresia , unde α este o constanta pozitiva, sa se determine expresia fortei ce deriva din acesta.

Rezolvare:

;

Pentru a lucra in coordonate carteziene se foloseste expresia potentialului scrisa cu aceste coordonate:

,

,

,

.

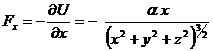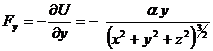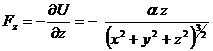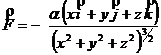
Potentialul unui camp are expresia , unde α si β sunt constante pozitive, iar r este distanta fata de centrul campului. Sa se determine:

a)     expresia fortei ce deriva din acest potential;

b)     valoarea maxima a fortei de atractie pe care acest camp o exercita asupra unei particule.

R: a) ; b) .

Momentul fortei si momentul cinetic

- momentul fortei;

- momentul cinetic;

- teorema mometului cinetic;

Pentru forte centrale momentul fortei este nul in raport cu centrul campului si momentul cinetic se conserva.

O planeta de masa m evolueaza in jurul Soarelui, de masa M, pe o elipsa. Distanta minima (periheliu) si maxima (afeliu) fata de Soare este r₁, respectiv r Calculati momentul cinetic al acestei planete in raport cu centrul Soarelui.

Rezolvare:

Forta de interactiune gravitationala intre planeta si Soare este:

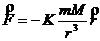
iar energia potentiala a planetei in campul gravitational al Soarelui este:

Miscarea planetei fiind in camp central, energia totala si momentul cinetic se conserva. In punctele in care distanta planetei fata de Soare este minima, respectiv maxima, aceste legi de conservare se scriu:

Rezolvand sistemul format din aceste doua ecuatii care au necunoscutele v₁ si v₂ se obtine:

.

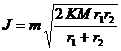Sa se exprime, in functie de momentul cinetic J, energia cinetica, energia potentiala si energia totala a unui satelit de masa m pe o orbita circulara.

R: ; ; .

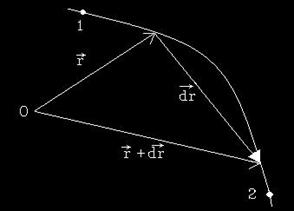
O deplasare infinit mica a punctului material pe traiectorie.

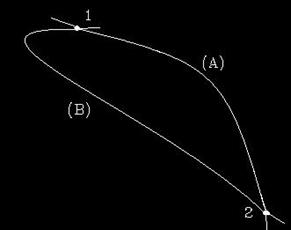
Traiectorii ale punctului material intre doua puncte in spatiu