NIVELMENTUL GEODEZIC

Nivelmentul geodezic se referǎ la determinarea inǎltimii unor puncte, situate pe suprafata terestrǎ, amplasate la distante mari unele de altele si ca atare va lua in considerare neparalelismul intre suprafetele de nivel, si de asemenea corectiile de sfericitate si refractie.

In functie de instrumentele utilizate la determinarea diferentelor de nivel, diferente cu ajutorul carora se calculeaza inǎltimile punctelor, nivelmentul geodezic se clasificǎ in: nivelment geometric, realizat cu ajutorul nivelelor, si nivelment trigonometric realizat cu ajutorul teodolitelor . In acest capitol nu se vor face referiri la celelalte metode de determinare a altitudinii (cotelor) punctelor, precum nivelmentul barometric, nivelmentul hidrostatic etc.

Inainte de a trece la tratarea efectivǎ a nivelmentului geodezic se va face o prezentare succintǎ a sistemelor de altitudini utilizate in geodezie.

7.1.Sisteme de altitudini

In functie de suprafata de referinta utilizata si semnificatia geometrica sau fizica, prin care se descrie pozitia punctelor pe suprafata terestrǎ, sistemele de altitudini se clasifica in:

Ø      dinamice;

Ø      ortometrice;

Ø      normale;

Ø      elipsoidale.

7.1.1.Sistemul de altitudini dinamice

Altitudinea dinamica a unui punct (H^D), notiune introdusǎ de Helmert in 1873, reprezintǎ raportul dintre diferenta de potential a doua suprafete de nivel, la valoarea gravitatii normale pentru latitudinea de 45⁰, raportata la elipsoidul de referinta.

Diferenta de potential, luatǎ cu semn schimbat, se referǎ la o suprafatǎ de nivel oarecare, care trece prin punctul "P" si suprafata de nivel zero care trece prin punctul "O" situat pe geoid.Relatia de calcul se prezintǎ sub forma:

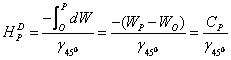(7.1)

unde :

W₀ - potentialul geoidului (W₀ =6263686 3).10 m²s^-2);

W_P - potentialul suprafetei de nivel care trece prin punctul "P".

Diferenta dintre se numeste numarul geopotential (C_P ) al punctului "P", notiune introdusa in anul 1955 de catre Asociatia Internationala a Geodezilor.

Numarul geopotential al unui punct situat pe suprafata terestrǎ reprezintǎ diferenta negativǎ dintre potentialul suprafetei de nivel care trece prin punctul considerat si potentialul geoidului.

Din punct de vedere dimensional altitudinile dinamice sunt exprimate in metri, insa ele nu au semnificatia geometrica, de a reprezenta inaltimea de la o anumita suprafata la punctul considerat.

Altitudinile dinamice pastreaza semnificatia fizica generala de impartire a numerelor potentiale cu o valoare constanta aleasa in mod conventional.

Cotele dinamice se caracterizeaza printr-o proprietate deosebita si anume: punctele situate pe o anumita suprafata de nivel au aceleasi cote dinamice

Pentru doua puncte "A" si "B" diferenta de nivel dinamica poate fi scrisa sub forma:

(7.2)

sau tinand seama de ecuatia fundamentala se poate scrie:

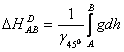(7.3)

In continuare relatia se poate transforma:

(7.4)

Efectuand notatiile:

(7.5)

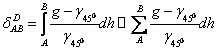(7.6)

relatia 7.4 devine:

(7.7)

unde:

- diferenta de nivel masurata;

- corectia dinamica pe traseul AB.

Sistemul de cote dinamice a stat la baza crearii retelei de nivelment din Europa de vest.

7.1.2.Sistemul de altitudini ortometrice

In cazul cotelor ortometrice suprafata de referinta este geoidul (notiune introdusa de Listing in anul 1873), iar altitudinea ortometrica () este segmentul liniei de forta cuprins intre pozitia punctului "P" de pe suprafata terestra si proiectia sa "P₀" pe geoid (fig.7.1).

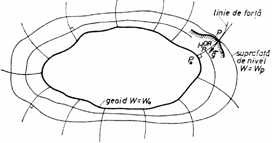
Fig.7.1. Suprafete de nivel

Geoidul este o suprafata de nivel echipotentiala, care are proprietatea, cǎ in oricare din punctele sale, directia liniilor de fortǎ este perpendicularǎ pe aceastǎ suprafatǎ . Tangenta la linia de fortǎ intr-un punct "P" dǎ directia gravitǎtii "" , materializatǎ de pozitia firului cu plumb. Geoidul este definit uzual ca suprafata medie a marilor si oceanelor prelungita imaginar pe sub continente.

Conform teoriei potentialului in orice punct din spatiu se poate scrie ecuatia fundamentala:

(7.8)

Prin aceastǎ ecuatie se stabileste dependenta dintre departarea "dh" si diferenta de potential "dW" existenta intre doua suprafete de nivel infinit apropiate.

Din relatia (7.8) rezultǎ:

(7.9)

sau:

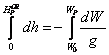(7.10)

integrand se obtine:

(7.11)

Prin ""s-a notat valoarea medie a gravitatiei in lungul liniei de fortǎ.

In functie de (7.11) se poate spune cǎ altitudinea ortometricǎ "H^OR"se obtine prin impǎrtirea numǎrului geopotential la valoarea medie a gravitǎtii in lungul liniei de fortǎ.

Dupǎ Moldoveanu [13] valoarea medie a gravitǎtii este datǎ de relatia:

(7.12)

unde:

g_P - valoarea gravitǎtii mǎsuratǎ la nivelul punctului "P".

7.1.2.1.Neparalelismul suprafetelor de nivel

In cadrul nivelmentului geometric s-a admis ipoteza cǎ suprafetele de nivel sunt concentrice si paralele intre ele. Dacǎ acest lucru este posibil pentru zone restranse, nu mai este posibil pentru zone mari, din domeniul Geodeziei. Este cunoscut, cǎ atat suprafata de nivel zero (geoidul), cat si suprafetele de nivel gravitationale au forma conventionalǎ de elipsoid. Suprafetele acestor elipsoizi nu sunt paralele, dupǎ cum se va vedea in continuare.

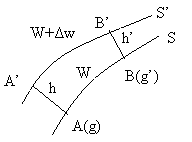
Fig.7.2.Sectiune prin douǎ suprafete de nivel

Deoarece suprafetele de nivel sunt suprafete echipotentiale, diferenta de potential dintre doua suprafete de nivel este o marime constanta. Rezulta ca, cresterea de potential (de lucru mecanic) nu depinde de drumul parcurs pentru trecerea unui punct de pe o suprafata de nivel pe alta.

Considerand douǎ suprafete de nivel gravitationale apropiate "S" si S' si douǎ traiectorii ortogonale AA' si BB' reprezentand directiile verticalelor (fig.7.2), atunci lungimile segmentelor pe verticale AA'= h si BB'= h' le considerǎm rectilinii, desi in realitate sunt usor curbilinii.

Utilizand lucru mecanic al fortei de greutate, pentru o masǎ unitarǎ, se poate afirma, cǎ aceasta nu depinde de drum atunci cand ne deplasǎm din punctul "A" in punctul B'. Astfel se poate scrie:

(7.13)

dar:

Avand in vedere ca lucrul mecanic (cresterea de potential) este egal cu intensitatea fortei inmultita cu deplasarea si ca pe o suprafata de nivel este nul, rezulta:

(7.14)

S-a notat cu "g" si g' intensitatea fortei de greutate in punctele "A" si "B", iar cu "h" si h' departarile dintre cele doua suprafete de nivel in dreptul punctelor anterior mentionate.

Conform relatiei (7.8) se poate scrie:

(7.15)

sau:

(7.16)

Cum insa intensitatile fortelor de greutate sunt diferite in puncte diferite, deci rezulta ca si .

Din masuratorile gravimetrice se cunoaste ca "g" variaza cu latitudinea. si considerand g º g, formula gravitatii normale stabilita de Clairaut are forma:

(7.17)

unde:

g_e- gravitatea normala la ecuator;

g - gravitatea normala in punctul de latitudine "B" ;

φ - latitudinea intr-un punct oarecare;

b- turtirea gravimetrica (f*), care se calculeaza, dupa Clairaut, cu relatia:

(7.18)

unde:

g_p - gravitatea normala la pol;

a - turtirea elipsoidului ;

a, b - semiaxa mare si respectiv mica a elipsoidului.

(7.19)

Observatie: In capitolul de Geodezie elipsoidalǎ pentru latitudinea geodezicǎ s-a utilizat notatia "B", iar pentru turtirea elipsoidului notatia "f".

Gravitatea normalǎ da valori care se refera la suprafata elipsoidului de rotatie ales.

Pentru a calcula marimea "g" a gravitatii normale la anumite inaltimi "H" de la elipsoid - inaltime luata pe directia normalei la suprafata acestuia in punctul respectiv, se aplica relatia:

(7.20)

in care:

- gradientul vertical al gravitatii normale,

( = - 0, 0848 gal/km);

H - inaltimea deasupra elipsoidului.

Semnul minus al gradientului vertical al gravitatii arata ca la o crestere a inaltimii "H" deasupra elipsoidului, corectia va fi negativa, adica la o marire a distantei de centrul de greutate al Pamantului gravitatea scade.

Valorile gravitatii normale sunt diferite in functie de elipsoidul de referinta considerat, astfel pentru elipsoidul international 1967, avem:

g_e=978,0318456 gal ;   

g_p=983,2177279 gal

Deoarece , cand mergem pe suprafata geoidului (sau pe alta suprafata de nivel gravitationala) de la ecuator la poli, gravitatea normala "g" creste, rezulta ca valoarea departarii "h" dintre cele doua suprafete de nivel va descreste.

Suprafetele de nivel gravitationale sunt mai apropiate intre ele la pol decat la ecuator. Cresterea relativa a gravitatii normale fiind de aproximativ 5 ,cand "j" creste de la 0⁰ la 90⁰ , rezulta o descrestere tot de 5 a departarii "h".

Cum departarile "h" considerate fata de suprafata de referinta reprezinta tocmai cotele ortometrice, rezulta ca o suprafata de nivel oarecare are la ecuator cota ortometrica egala cu 1000 m, aceeasi suprafata va avea la pol cota ortometrica egala cu 995 m.

Se observa o deosebire neta privind modul de stabilire a cotelor ortomerice, in comparatie cu cele cunoscute la Topografie, cand suprafetele de nivele se considerau plane sau sferice.

Intrucat nivelmetrele realizeaza linii de viza intr-un plan orizontal, se impune introducerea unor corectii pentru a realiza trecerea de la marimile masurate dupa plane orizontale paralele la marimi corespunzatoare suprafetelor de nivel elipsoidale si neparalele.

Presupunem ca se executa un nivelment geometric intre doua puncte "A" si "B" pentru a se stabili diferenta de nivel dintre aceste puncte.

Considerand traseul mai sus mentionat impartit in niveleurile 12,23,., iar diferentele de nivel corespunzatoare notate cu , respectiv lecturile inapoi notate cu "r" si cu "v" lecturile inainte pe mirǎ, pentru cazul primului niveleu se poate scrie:

(7.21)

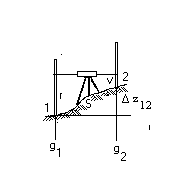
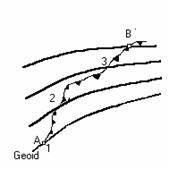
Fig.7.3 Drumuirea de nivelment

S-a notat cu "g₁" si "g₂" intensitatea fortei de greutate in punctele 1 si 2, iar cu "r" si "v" lecturile pe mirele verticale situate in aceste puncte. Dezvoltand relatia de mai sus obtinem:

(7.22)

sau adunand si scazand "rg₂" obtinem:

(7.23)

de unde:

(7.24)

In relatia (7.24) termenul reprezinta corectia ce trebuie aplicata diferentei lecturilor pe mira pentru a obtine diferenta de nivel ortometrica intre cele doua puncte.

Pe intregul traseu avem:

(7.25)

sau notand = Δh_AB, diferenta de nivel intre punctele "A" si "B", rezultata din masuratori si considerand ca

r = constant, putem scrie:

(7.26)

Mai simplu:

₁ (7.27)

Corectia "c₁"_, care se aplica diferentei de nivel masurate in vederea obtinerii diferentei de nivel ortometrice se calculeaza cu relatia:

(7.28)

unde:

H_med- altitudinea medie;

- diferenta de latitudine;

- latitudinea medie;

- coeficient ce indica turtirea gravimetrica.

Corectia ortometrica este negativa cand se merge spre pol si pozitiva in caz contrar. In practica se aplica pe tronsoane de nivelment convenabil alese.

Relatia practicǎ utilizatǎ pentru calculul corectiei ortometrice (), datǎ de [13], se prezintǎ sub forma:

(7.29)

unde:

γ₀-valoarea gravitǎtii normale la latitudinea de 45⁰;

- valorile medii ale gravitǎtii de-a lungul liniilor de fortǎ ce trec prin punctele "A" si "B";

H_A si H_B- valorile aproximative ale cotelor punctelor "A" si "B";

Δ_AB - diferenta de nivel mǎsuratǎ.

7.1.3.Sistemul de altitudini normale

Notiunea de altitudine normalǎ a fost introdusa in anul 1945 de M.S.Molodenski, in scopul de-a elimina dezavantajul cotelor ortometrice, provenit din:

Ø   raportarea la suprafata ondulata a geoidului;

Ø   utilizarea gravitǎtii medii in lungul liniei de fortǎ.

In acest scop se renunta la suprafata geoidului ca suprafata de referinta si se introduce o suprafata teoretica apropiata de geoid, care nu are ondulatii si care se numeste cvasigeoid sau cogeoid.In al doilea rand se propune utilizarea campului gravitǎtii normale in locul campului gravitǎtii.

Cvasigeoidul este suprafata de nivel astfel construitǎ incat segmentul de normalǎ la elipsoid este egal cu anomalia altitudinii.

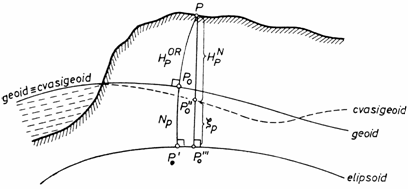
Fig.7.4. Sistemul de altitudini ortometrice si normale

Altitudinea normalǎ se noteazǎ cu (fig.7.4) si se obtine prin impǎrtirea numǎrului geopotential la o valoare medie a gravitǎtii normale:

(7.30)

unde:

-valoarea medie a acceleratiei normale a gravitǎtii in lungul normalei la elipsoid

Trecerea de la diferentele de nivel mǎsurate la cele normale se face prin aplicarea corectiilor normale. Aceste corectii se obtin din corectiile ortometrice, prin inlocuirea gravitǎtii medii cu gravitatea normalǎ medie in lungul liniei de fortǎ si a altitudinii cu altitudinea normalǎ:

(7.31)

Dupǎ Dima [7], cotele normale se obtin prin corectarea rezultatelor nivelmentului geometric cu asa numita corectie normala :

(7.32)

unde: cei trei termeni corectivi au semnificatia:

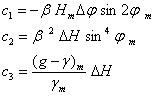(7.33)

Se observa ca termenul corectiv "c₁" este insasi corectia ortometrica sferoidicǎ si este datorat neparalelismului suprafetelor de nivel.

Termenul corectiv "c₂" este datorat reliefului terenului; in terenurile de ses nu se ia in consideratie pentru ca

DH = 0.

Termenul c₃ este datorat structurii neuniforme a scoartei terestre in zona in care se fac masuratorile. In acest termen corectiv intra anomalia medie a fortei de gravitate (g - g)_m si intensitatea medie teoretica g_m a acestei forte, valorile lor obtinandu-se prin masuratori gravimetrice.

De mentionat faptul ca reteaua nivelmentului de stat din tara noastra este exprimata in cote normale.

Formula recomandatǎ, de instructiunile in vigoare , pentru trecerea de la diferentele de nivel mǎsurate la diferente de altitudini normale este:

unde:

- valoarea acceleratiei gravitǎtii normale la altitudinea medie calculatǎ pentru latitudinea medie a celor douǎ puncte intre care se executǎ mǎsurǎtorile de nivelment geometric;

- valoarea medie a anomaliilor acceleratiei greutǎtii corespunzǎtoare celor douǎ puncte;

- valorile normale ale acceleratiei gravitǎtii pentru proiectiile pe elipsoid a celor douǎ puncte.

7.1.4. Sisteme de altitudini elipsoidale

Revenind la suprafetele de referintǎ, prezentate in capitolele anterioare, reiterǎm, cǎ pentru pozitionarea planimetricǎ a punctelor suprafata de referintǎ este elipsoidul, iar pentru altitudini geoidul.

Pentru a nu avea doua suprafete de referinta separate, una pentru planimetrie si alta pentru altimetrie, este necesar ca in lucrari speciale sǎ se utilizeze o singurǎ suprafatǎ de referintǎ - elipsoidul de rotatie.

Cotele elipsoidale sunt date de inǎltimile punctelor, luate pe normala la elipsoid, de la punctele situate pe suprafata terestrǎ panǎ la proiectia acestora pe elipsoid.

Expresiile de calcul sunt date de relatia :

(7.35)

unde: -cota elipsoidalǎ a punctului "P" ;

N - ondulatia geoidului- inaltimea (pe verticala) a geoidului fata de elipsoid ;

ζ -anomaliile altitudinilor, inǎltimea cvasigeoidului fatǎ de elipsoid.

7.2.Nivelmentul geometric geodezic

7.2.1. Consideratii generale

Baza altimetricǎ a ridicǎrilor topografice in vederea intocmirii planurilor topografice la diferite scǎrii, o formeazǎ reteaua niveliticǎ de stat.

Nivelmentul geometric de stat cuprinde retelele de nivelment geometric de ord. I - IV si nivelmentul de intravilan, care se caracterizeazǎ printr-o inalta precizie.

Reteaua de nivelment de ord. I cuprinde liniile de nivelment, care se leaga cu liniile de nivelment similar al tarilor vecine , legand punctele fundamentale altimetrice. Reteaua de ord.I (fig.4.5) formeaza poligoane inchise cu lungimi de 1200-1500 km ce se dezvoltǎ, in general, in lungul cailor ferate.

Drumuirile de nivelment de ord.I se executa pe tronsoane dus - intors, astfel ca fiecare diferenta de nivel pe tronson sa rezulte ca media a 8 valori. Se admite la 1 km de drumuire o eroare medie patratica intamplatoare h 0.5 mm si una sistematica de s 0.05 mm; toleranta pentru eroarea medie patratica este de T = 2 mm.

Reteaua de ord.II se compune din liniile nivelitice sprijinite pe puncte de nivelment de ord. I, formand poligoane cu perimetrul de 500 - 600 km.

Reteaua de ord.II se desfasoara in lungul cailor ferate, soselelor, fluviilor si raurilor mari si se executa dus-intors cu medii din 4 valori. Toleranta totala admisa este de T = 5 mm , iar eroarea sistematica trebuie sa fie mai mica de 0.2 mm/ km.

Reteaua de ord.III se dezvolta in interiorul poligoanelor de ord.I si II asa incat sa formeze poligoane sau traverse cu perimetre de 150-200 km, recomandandu-se ca intr-un poligon de ord II sa existe 6-9 poligoane de ord. III.

Reteaua de ord III se executa dus-intors, cu medii de 4 valori cu o precizie care sa asigure obtinerea unei neinchideri in poligon inchis sau drumuiri cu doua capete, care sa nu depaseasca toleranta totala T = 10 mm .

Reteaua de ord.IV indeseste reteaua de ord..I, II si III, ea se dezvolta astfel incat sa formeze poligoane inchise cu perimetrul de 100 km sau traverse avand lungimi de 100 sau 50 km .

Nivelmentul de ord. IV se executa numai dus, cu medii din doua valori cu o precizie care sa asigure o neinchidere ce nu depaseste T = 20 mm .

Nivelmentul geometric geodezic intravilan serveste la rezolvarea unor probleme speciale de ordin tehnico-ingineresc. El corespunde ca precizie cu ord. II, III si IV si se executa sub forma de poligoane sau traverse, legandu-se obligatoriu de reteaua de stat.

Inaltimile punctelor ce alcatuiesc retelele nivelitice de orice ordin au ca origine un punct de sprijin, de baza, numit punct fundamental sau punct de nivel zero.

Cota acestui punct se determinǎ fatǎ de nivelul mediu al marilor si oceanelor, determinat din observarea acestui nivel pe o perioada de cca. 30-50 ani.

Problema localizǎrii pozitiei verticale, fatǎ de geoid, a unui reper de referintǎ situat pe tǎrmul mǎrii se reduce la a determina pozitia nivelului mediu al mǎrii. Pentru aceasta trebuie sǎ se inregistreze variatia nivelului local instantaneu al mǎrii fatǎ de pozitia zero a unui instrument de mǎsurare a mareelor (maregrafe).Ca o medie a nivelului local instantaneu al mǎrii se determinǎ nivelului local al mǎrii

Intrucat nivelul mediu al mǎrilor difera de la un loc la altul, a fost necesara legarea tuturor punctelor altimetrice fundamentale la nivel european si s-a adoptat, in 1958, ca punct de plecare, punctul zero (Kronstadt) de la Marea Baltica.

In decursul timpului s-au utilizat ca puncte fundamentale: zero Sulina 1857, in Ardeal zero Marea Adriaticǎ (1923), zero Marea Neagrǎ, cu punct fundamental o placǎ de bronz, cu inǎltimea de 2.48 m fatǎ de zero mirǎ maregraf Constanta, zero Marea Balticǎ (1951-1975), iar la ora actualǎ sistemul de altitudini este denumit : "Sistem Marea Neagra zero 1975", cu punctul fundamental plasat in capela militarǎ Constanta.

7.2.2.Compensarea retelelor de nivelment prin metoda     masuratorilor conditionate

Metoda observatiilor conditionate utilizatǎ la rezolvarea retelelor de nivelment este cunoscutǎ sub denumirea de metoda poligoanelor, intrucat numǎrul conditiilor geometrice este dat de numǎrul poligoanelor reale si fictive existente in retea.

Numǎrul total de conditii geometrice "r", intr-o retea de nivelment se stabileste cu relatia:

(7.36)

unde:

n_pr- numǎrul poligoanelor reale;

n_pf- numǎrul poligoanelor fictive;

N_V- numǎrul punctelor vechi.

Metoda observatiilor conditionate este mai avantajoasǎ decat metoda observatiilor indirecte, in cazul cand, numǎrul punctelor noi este mai mare decat numǎrul conditiilor geometrice.

Metoda observatiilor conditionate se aplica la retelele nivelitice independente sau dependente ce apartin ord I si II. Fie spre exemplu reteaua nivelitica independenta formata din poligoanele inchise I, II, III, IV (fig. 7.5. ).

Introducem notatiile:

h₁, h_{2, .} h₈ - diferentele de nivel masurate;

(h₁₎, (h_{2), .} (h₈) - diferentele de nivel probabile;

v₁, v_{2, .} v₈ - corectiile probabile ale diferentelor de nivel masurate;

S₁, S_{2, .} S₈ - lungimile traverselor ce formeaza cele patru poligoane inchise;

p₁, p_{2, .} p₈ - ponderile marimilor masurate.

Conform relatiei (7.36) se calculeazǎ numǎrul conditiilor geometrice :

Fig.7.5.Retea de nivelment neconstransǎ

Daca se respecta sensul de crestere a declivitǎtiilor, indicat pe figura prin sageti, atunci in baza unui sens general de parcurgere (sensul orar), pot fi formate conditiile :

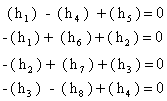
dar:

si astfel cele patru conditii geometrice conduc la patru ecuatii de corectii de forma:

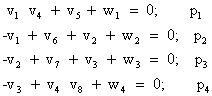
unde:

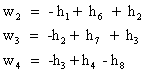
se numesc neinchideri nivelitice.

p_i - ponderile tronsoanelor de nivelment

Pentru nivelmentul geometric ponderea unui tronson este data de inversul lungimii traseului :

(7.42)

Sistemul de corectii obtinut este nedeterminat si prin aplicarea conditiei [pvv] = minim,poate fi transformat intr-un sistem determinat , de forma:

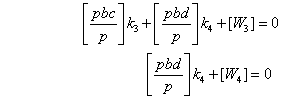
Coeficientii ecuatiilor normale se pot calcula conform consideratiilor teoretice prezentate in 4.3.5, sau se pot exprima, in mod direct, in functie de lungimea traseelor de nivelment.

Pentru aceasta, se pleacǎ de la matricea coeficientilor corespunzatoare sistemului ecuatiilor de corectii:

(7.44)

in functie de care se culeazǎ:

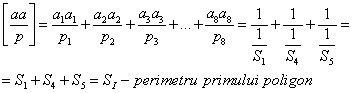
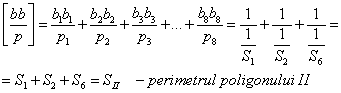
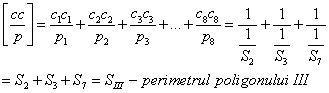
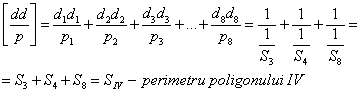
= - S₁ sectiunea comuna poligoanelor I-II

= 0 sectiunea comuna poligoanelor I-III

= - S4 sectiunea comuna poligoanelor I-IV

s.a.m.d.

Cu acesti coeficienti sistemul ecuatiilor normale are o forma simpla si poate fi scris direct dupa schita traseelor, respectiv:

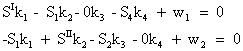
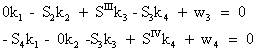(7.46)

Rezolvand acest sistem obtinem corelatele k₁, k₂, k₃, k₄, cu ajutorul carora determinam corectiile, folosind relatiile:

(7.47)

Tinand seama de valoarea coeficientilor ecuatiilor de corectii se obtine:

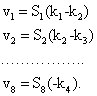(7.48)

Corectiile diferentelor de nivel date de (7.48) pot fi scrise direct folosind urmǎtoarele reguli:

Ø   corectia unei diferente de nivel mǎsuratǎ pe o sectiune interioarǎ retelei, este datǎ de lungimea sectiunii inmultitǎ cu diferenta dintre corelatele poligoanelor adiacente (sensul diferentei coincide cu sensul general de scriere a conditiilor);

Ø   corectia unei diferente de nivel mǎsuratǎ pe o sectiune de contur a retelei este datǎ de lungimea sectiunii inmultitǎ cu corelata poligonului din care face parte sectiunea.

Diferentele de nivel compensate se obtin dupa relatia:

Eroarea medie patratica a unitatii de ponderi se calculeaza cu formula:

unde:

r- nr. ecuatiilor de conditie

Dupa obtinerea diferentei de nivel compensate se calculeaza cotele punctelor nodale (pornind de la un punct de cota cunoscuta, sau luat arbitrar) si apoi cotele punctelor de pe sectiuni.

Compensarea retelelor de nivelment va fi tratata si pentru cazul retelelor de nivelment dependente , retele care contin doua sau mai multe puncte de cote cunoscute.

Fie spre exemplu reteaua nivelitica formata din 4 poligoane inchise si 2 puncte "A", "B" ale caror cote sunt cunoscute (fig.7.6.).Acest caz corespunde retelelor nivelitice de ord II si III. Daca traseul de nivelment ce se sprijina pe punctele date "A", "B" se considera inchis dupa traseul imaginar reprezentat punctat formand poligonul "V", atunci ecuatiile de corectii se prezintǎ sub forma:

Fig. 7.6.Retea dependentǎ de nivelment

Conform figurii se poate scrie direct sistemul ecuatiilor normale:

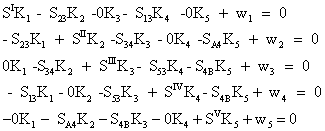(7.52)

unde lungimea poligonului fictiv "V" este:

(7.53)

Din relatia (7.52) se observǎ cǎ sistemul ecuatiilor normale poate fi scris direct de pe schita retelei. Indiferent de configuratia sa, fiecǎrui poligon (real sau fictiv) ii corespunde o ecuatie normalǎ constituitǎ din:

Ø   coeficientul corelatei de pe diagonala principalǎ, cǎruia ii corespunde lungimea (in km) a perimetrului poligonului considerat;

Ø   coeficientii corelatelor poligoanelor adiacente, care sunt egali cu lungimea laturilor adiacente, luati cu semn schimbat;

Ø   corelatele poligoanelor adiacente, reale sau fictive;

Ø   termenul liber, egal cu neinchiderea in poligon.

In afarǎ de metodele prezentate, compensarea retelelor de nivelment geometric de ordinul III si IV se poate realiza prin metoda aproximatiilor succesive.

In principiu, metoda constǎ in exprimarea corelatelor poligoanelor(k_i) in functie de neinchiderea diferentelor de nivel (w_i), raportate la perimetrele poligoanelor Sⁱ plus corectiile .

Prin introducerea acestor expresii in sistemul initial al corelatelor se obtine un nou sistem normal de corelete cu neinchiderile .Dupǎ care se exprimǎ in functie de raportate la perimetrele poligoanelor Sⁱ plus corectiile , s.a.m.d., operatiunile se repetǎ panǎ cand neinchiderile diferentelor de nivel pe poligoane tind spre zero.Prezentarea in detaliu a metodei se regǎseste in [7].

7.2.3.Compensarea retelelor de nivelment prin metoda     masuratorilor indirecte

O retea de nivelment geometric este alcǎtuitǎ din reperele de nivelment intre care se efectueaza masuratori in vederea determinarii diferentelor de nivel si a lungimii traseelor pe care se efectueaza observatiile.

Pentru a se efectua calculele de compensare, trebuie sa se cunosca sau sa se determine:

- Diferentele de nivel masurate Δh_ij prin metoda nivelmentului geometric si reduse unitar la unul din sistemele de altitudini cunoscut (functie de cerintele lucrarii);

- Lungimile traseelor urmate pentru determinarea diferentelor de nivel se determina concomitent cu efectuarea observatiilor si ele sunt necesare pentru determinarea ponderilor masuratorilor. Pentru unele retele poate fi considerat ca element de calcul al ponderii numarul statiilor efectuate pentru determinarea diferentei de nivel dintre doua repere;

- Altitudinea (H_i) a unuia sau a mai multor repere de nivelment din reteaua considerata;

- Informatii cu privire la matricea ponderilor observatiilor necesare la construirea modelului functional-stochastic

Pentru o prelucrare prin metoda observatiilor indirecte este necesar ca numarul masuratorilor sa fie mai mare decat numarul necunoscutelor implicate in model.

Aceasta metoda de compensare mai poarta numele de metoda nodurilor deoarece ecuatiile corectiilor se scriu in jurul fiecǎrui punct nou, denumit si nod. Metoda se utilizeaza, in general, la nivelmentul de ord. III si IV. Se trateaza analog cu metoda planimetrica a variatiei coordonatelor si s-ar putea numi ca atare si metoda variatiei altitudinilor.

Pentru prelucrare se vor deduce corectii pentru masuratori si respectiv pentru altitudinile provizorii:

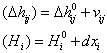
Ecuatiile corectiilor au forme diferite in functie de tipul punctelor intre care se scriu si anume:

Ø   intre doua puncte vechi nu se executa o noua masuratoare directa, fara puncte intermediare Aceasta se observa si pe figura 7.6. de care se va tine seama la deducerea formulelor folosite in prelucrare.

Ø   intre un punct vechi "A" si un punct nou "1" se poate scrie:

(7.55)

de unde rezulta:

(7.56)

Ø   Intre doua puncte noi:

(7.57)

de unde rezulta:

(7.58)

Considerand reteaua neconstransǎ din figura 7.5., in care se cunoaste cota punctului "A", se mǎsoarǎ diferentele de nivel intre puncte, pe baza cǎrora se determinǎ cotele provizorii ale punctelor nodale 1,2,3 si 4.

Pentru scrierea ecuatiilor de corectii se introduc notatiile:

Ø   (H₁), (H₂), (H₃),(H₄) - cotele cele mai probabile ale punctelor nodale;

Ø   - cotele aproximative ale punctelor nodale;

Ø   dx₁, dx₂, dx₃, dx₄ - corectiile probabile ale cotelor aproximative;

Ø   h₁, h₁,. h₈ - diferentele de nivel mǎsurate.

Conform acestor notatii se poate scrie:

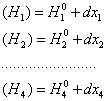
Cotele provizorii se obtin pornind de la cota cunoscutǎ a punctului "A", adunand algebric (in functie se sensul de crestere a declivitǎtii), pe diferite trasee, diferentele de nivel mǎsurate.

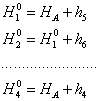
Ecuatiile corectiilor se pot stabili cu usurinta, direct de pe figura, in jurul fiecǎrui nod, tinand seama de ecuatiile stabilite anterior, si de faptul cǎ pentru fiecare diferentǎ de nivel mǎsuratǎ intre nodurle existente se va scrie o ecuatie de corectii.

Ecuatiile corectiilor pentru reteaua de nivelment neconstransǎ (fig 7.5 ) se prezentata sub forma:

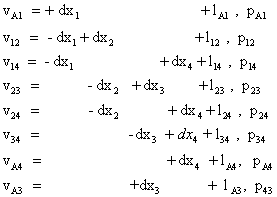
in care:

Sistemul de erori se rezolva dupa metoda masuratorilor indirecte de precizii diferite, punand conditia [pvv] = minim. Se obtine sistemul ecuatiilor normale:

Coeficientii necunoscutelor si termenii liberi se obtin conform metodologiei prezentatǎ in 4.3.3.

O scriere directǎ a ecuatiilor normale se realizeazǎ in functie de ponderile ecuatiilor, astfel, pentru prima ecuatie normalǎ se poate sctie:

Se observa ca sistemul ecuatiilor normale poate fi format de pe schita retelei, indiferent de complexitatea sa, fiecarui punct nou corespunzandu-i o ecuatie normala constituita din urmatorii termeni:

Ø      coeficientul necunoscutei de pe diagonala principala "P_i", corespunzator nodului "i", pentru care se scrie ecuatia, este egal cu suma ponderilor liniilor care converg in nodul mentionat ;

Ø      in ecuatie mai intervin necunoscutele corespunzatoare nodurilor cu care punctul "i" este in legatura cu coeficientii respectivi egali cu - p_ij ;

Ø      termenul liber , notat in continuare cu "E", este format dintr-o suma de produse, intre ponderi si termenii liberi ai ecuatiilor de erori scrise pentru punctul "i", in care semnul plus se ia pentru liniile care intra in punct ,iar semnul minus pentru liniile care pleaca din punct.

In acest fel ecuatia normala , pentru reteaua considerata se prezinta sub forma:

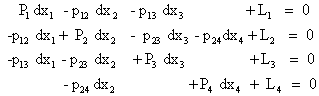(7.65)

Prin rezolvarea sistemului cu una din metodele cunoscute de la teoria de prelucrare a marimilor geodezice, se obtin corectiile : dx₁, dx₂,.. dx₄, cu ajutorul carora se calculeaza valorile probabile ale cotelor:

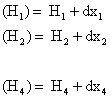
Eroarea medie patratica se calculeaza cu formula:

in care:

n - numarul ecuatiilor de erori ( in cazul exemplului considerat n= 8);

k - numarul de necunoscute ce se calculeaza ( in cazul exemplului considerat k=4).

7.3.Nivelmentul trigonometric geodezic

Nivelmentul trigonometric se utilizeazǎ la determinarea altitudinii punctelor retelelor geodezice, in retele geodezice tridimensionale pentru determinarea altitudinilor elipsoidale si in Geodezia fizicǎ pentru determinarea deviatiei verticalei si a ondulatiei geoidului.

Problema principalǎ la determinarea altitudinilor prin nivelment trigonometric o constituie efectul refractiei atmosferice verticale si a sfericitǎtii. Refractia verticalǎ influenteazǎ valoarea unghiurilor zenitale mǎsurate si implicit si a diferentelor de nivel determinate.De asemenea, sfericitatea influenteazǎ diferentele de nivel, determinate intre douǎ puncte.

De la cursul de Topografie se cunoaste cǎ valoarea corectiei totale de sfericitate si refractie se calculeazǎ cu relatia:

(7.68)

unde:

k- coeficientul de refractie (k=00.26, pentru latitudinea B=0⁰90⁰);

R- raza medie de curburǎ a sectiunilor eliptice ce trec prin punctele "P_i" si "P_j":

(7.69)

Valoarea celor douǎ raze de curburǎ se calculeazǎ cu relatia:

(7.70)

unde:

A_ij - azimutul sectiunii normale ;

M_i si "N_i- razele principale de curburǎ ale elipsoidului de referintǎ.

La studierea fenomenului de refractie. de multe ori, suprafata geoidului se inlocuieste cu suprafata sferei medii Gauss de razǎ , fǎrǎ introducerea unor erori superioare celor generate de acceptarea altor aproximatii.

7.3.1.Refractia atmosfericǎ verticalǎ

Dacǎ se considerǎ punctele "P_i" si "P_j" in care s-au efectuat observatii unghiulare verticale, care au fost corectate cu componentele deviatiei verticale pe directia celor douǎ puncte (v.1.11.3.), datoritǎ fenomenului refractiei atmosferice verticale se mǎsoarǎ distantele zenitale in locul valorilor reale (fig.7.7). Conform figurii se poate scrie:

(7.71)

unde:

- unghiurile de refractie intre cele douǎ puncte

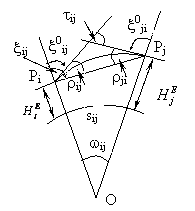
Fig.7.7. Refractia terestrǎ verticalǎ

Unghiul "τ" format de tangentele din punctele "P_i" si "P_j" se numeste unghiul refractiei totale a cǎrui expresie de calcul este datǎ de relatia:

Notand cu ""curbura variabilǎ a razei de luminǎ , refractia totalǎ poate fi determinatǎ teoretic cu relatia:

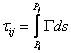(7.73)

unde:

ds- elementul de arc al arcului .

Relatia (7.3) este numai teoretic aplicabilǎ, pentru cǎ aceasta ar necesita mǎsurǎtori de temperaturǎ si presiune din punct in punct , in lungul razei de luminǎ, care, evident sunt posibile numai teoretic.

In practicǎ, avand in vedere cǎ lungimea vizelor la nivelmentul trigonometric este de panǎ la 7km, se acceptǎ o valoare constantǎ a curburii razei de luminǎ, ceea ce inseamnǎ cǎ arcul de curburǎ dintre cele douǎ puncte poate fi aproximat cu un arc de cerc .In baza acestei aproximǎri se poate scrie:

(7.74)

De asemenea, ca urmare a aproximǎrii acceptate , raza de curburǎ devine constantǎ. In urma integrǎrii relatiei (7.3) rezultǎ:

(7.75)

O altǎ aproximatie acceptatǎ este aceea de a inlocui lungimea arcului din relatia de mai sus ,cu distanta de pe elipsoidul de referintǎ "s_ij".

Asimiland elipsoidul cu sfera de razǎ medie Gauss se poate inlocui lungimea arcului de cerc cu raza medie deinmultitǎ cu unghiul la centru si astfel relatia (7.5) devine:

(7.76)

unde:

R_m - valoarea medie a razelor de curburǎ in cele douǎ puncte intre care se determinǎ diferenta de nivel;

R_r - raza de curburǎ a razei de luminǎ dupǎ care se fac observatiile zenitale.

k - coeficient de proportionalitate denumit si coeficient de refractie:

(7.77)

Din relatiile (7.74) si (7.76) rezultǎ expresia de calcul a valorii unghiului de refractie:

(7.78)

Din triunghiul OP_iP_j (fig.7.7) se poate deduce cǎ:

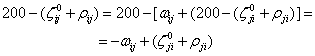(7.79)

sau:

(7.80)

sau:

(7.81)

Inlocuind valoarea expresiei (7.81) in relatia (7. 76) si efectuand calculele se obtine coeficientul de refractie "k":

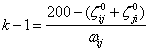(7.82)

Refractia atmosfericǎ este o functie periodicǎ, dependentǎ de mai multi factori, dintre care cel mai important este temperatura atmosferei. Acest factor face ca refractia atmosfericǎ terestrǎ sǎ fie o consecintǎ directǎ a incǎlzirii solului.

In variatia diurnǎ (24 ore) a refractiei verticale se remarcǎ o caracteristicǎ de stabilitate intre orele 10 si 15, perioadǎ in care se recomandǎ sǎ se execute mǎsurǎtirile geodezice zenitale.

Pentru lucrǎrile curente se acceptǎ coeficientul de refractie(calculat de Gauss) k=013, valoare utilizatǎ si in statiile totale pentru calculul corectiilor fizice, iar pentru tara noastrǎ coeficientul adoptat este k =0.14.

Pentru a diminua efectul refractiei atmosferice este indicat, sǎ se mǎsoare ambele distante zenitale, pe cat posibil simultan (observatii zenitale reciproce si simultne)

7.3.2.Nivelmentul trigonometric geodezic reciproc si     simultan

Pentru a stabili relatia de calcul a diferentei de nivel dintre punctele "P_i" si "P_j", trebuie luat in considerare sistemul de altitudini in care va fi utilizatǎ diferenta.

In cazul sistemelor de altitudini ce au ca suprafata de referintǎ geoidul, nu este necesarǎ aplicarea corectiilor de reducere a observatiilor zenitale la normala la elipsoid, iar in cazul altitudinilor elipsoidale se aplicǎ aceste corectii.

Cu aceste precizǎri si intr-un caz si in altul se parcurg etapele:

Ø   se mǎsoarǎ unghiurile zenitale ;

Ø   se determinǎ distanta dintre punctele P_i si P_j , din coordonate;

Ø   se acceptǎ urmatoarele ipoteze simplificatoare:

se considerǎ observatiile executate la sol (I_i=S_i=I_j=S_j), urmand ca acestea sǎ se introducǎ in formulele finale;

se neglijeazǎ ondulatiile geoidului si deviatiile de la verticalǎ a normalei la elipsoid;

se asimileazǎ distanta calculatǎ din coordonate cu distanta redusǎ la geoid.

Pentru a calcula diferenta de nivel dintre pinctele "P_i" si "P_j", in triunghiul P_iP_jO (fig 7.8.) se poate aplica teorema sinusului sau a tangentei.Prin aplicarea teoremei tangentei se obtine:

(7.83)

Asimiland triunghiul P_iP_jO cu triunghiul ABC, se pot face , in continuare, asimilǎrile:

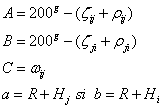(7.84)

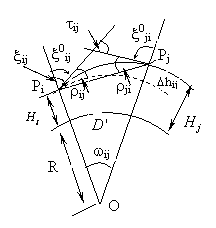
Fig.7.8. Nivelmentul trigonometric

Inlocuind (7.84) in (7.83) se obtine:

(7.85)

de unde rezultǎ:

(7.86)

Deoarece "ω_ij" este un unghi mic (pentru lungimea laturilor de triangulatie de 30 km, ω_ij<30^c), se poate asimila valoarea functiei cu valoarea argumentului:

(7.87)

Datoritǎ asimilǎrii geoidului cu sfera de razǎ medie Gauss se poate scrie:

(7.88)

Inlocuind relatiile (7.87) si (7.88) in (7.86) se obtine urmǎtoarea relatie de calcul:

(7.89)

in care :

(7.90)

unde: sunt altitudinile aproximative ale celor douǎ puncte determinate de pe hartǎ.

Dacǎ se ia in considerare inǎltimile instrumentelor din cele douǎ puncte (I_i, I_j) si inǎltimile semnalelor (S_i, S_j ) diferenta de nivel trebuie corectatǎ cu:

Ø   (I_i-S_j) pentru punctul "P_i", (pentru a determina Δh_ij);

Ø   (I_j-S_i) pentru punctul "P_j", (pentru a determina Δh_ji);

intrucat Δh_ij=- Δh_ji media celor douǎ corectii va fi:

(7.91)

Cu aceasta diferenta de nivel trigonometric reciproc si simultan este datǎ de relatia:

(7.92)

7.3.3.Nivelmentul trigonometric geodezic unilateral

In practicǎ , de regulǎ, se fac numai observatii unghiulare verticale unilaterale, situatii cand refractia atmosfericǎ are o contributie semnificativǎ, fapt pentru care se va tine seama de aceasta.

Dacǎ din relatia (7.80) se extrage valoarea pentru distanta zenitalǎ "ζ_ji" se obtine:

(7.93)

Prin introducerea rel. (7.93): in (7.89) si tinand seama de rel. (7.81), (7.82) se obtine:

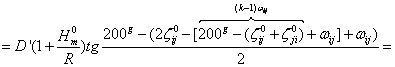
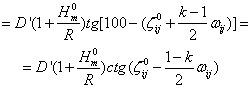(7.94)

Dacǎ se dezvoltǎ in serie Taylor cotangenta din relatia de mai sus se poate scrie:

(7.95)

In rel. (7.95) se inlocuieste "ω_ij" cu , si astfel, formula de calcul a diferentei de nivel, in cazul nivelmentului trigonometric unilateral se prezintǎ sub forma:

(7.96)

7.3.4Metode de realizare a nivelmentului trigonometric

In cazul nivelmentului trigonometric unilateral se aplicǎ:

Ø   metoda intersectiei inainte;

Ø   metoda intersectiei inapoi;

Ø   metoda drumuirii de nivelment geodezic etc.

Metoda intersectiei inainte -constǎ in mǎsurarea distantlor zenitale (unghiurilor zenitale) de la punctele cunoscute spre punctul a cǎrui cotǎ dorim sǎ o determinǎm.

Fig.7.9 Metoda intersectiei inainte

Considerand cunoscute cotele punctelor A,B,C,D, (fig.7.9.) se determinǎ diferentele de nivel spre punctul "P" cu relatia (7.96.). Cota punctului "P" se determinǎ cu relatia:

(7.97)

Valoarea cea mai probabilǎ a cotei punctului nou se determinǎ cu relatia:

(7.98)

in care:

P_A, P_B, P_C, P_D - ponderile cotelor,care se determinǎ cu relatiile:

(7.99)

- cota punctului "P" determinate din punctele vechi.

Metoda intersectiei inapoi - constǎ in mǎsurarea unghiurilor zenitale (distantelor zenitale) , in punctul a cǎrei cotǎ dorim sǎ o determinǎm spre punctele de cotǎ cunoscutǎ. Pe baza observatiilor efectuate se calculeazǎ diferentele de nivel cu rel.(7.96) si apoi cota punctului "P":

(7.100)

Cota ce mai probabilǎ a punctului "P" se determinǎ ca si in cazul intersectiei inainte (rel.7.98.).

Drumuirea de nivelment geodezic - este formatǎ    dintr-un traseu de nivelment unilateral sprijinit la capete pe puncte de cote cunoscute (H_A si H_B), traseu care trece prin punctele retelei de triangulatie a cǎror cote dorim sǎ le determinǎm. Diferentele de nivel dintre puncte se calculeazǎ cu relatii de forma (7.96), iar neinchiderea pe cote se stabileste cu:

(7.101)

unde:

(7.102)

in care : distantele se exprimǎ in "km", iar toleranta in "m",

Corectia de neinchidere unitarǎ se calculeazǎ cu relatia:

(7.103)

Eroarea de neinchidere pe cote se repartizeazǎ diferentelor de nivel mǎsurate, proportional cu distantele dintre puncte denmultite cu eroarea unitarǎ, luatǎ cu semn schimbat:

(7.104)

unde:

- diferentele de nivel compensate;

- diferentele de nivel mǎsurate;

- corectia unitarǎ ;

d_ij - distantele aferente diferentelor de nivel mǎsurate.

Cu diferentele de nivel compensate se calculeazǎ cotele

definitive ale punctelor:

(7.105)

Cu referire la precizia cotelor, obtinute prin nivelment trigonometric, trebuie reamintit cǎ, datoritǎ ipotezelor simplificatoare introduse in modelul functional stochastic, aceasta este mai micǎ decat in cazul nivelmentului geometric geodezic.

Metoda nivelmentului trigonometric geodezic este indicatǎ in cazul determinǎrii cotelor retelelor de triangulatie in regiunile de deal si munte.