Reprezentarea simbolica a marimilor sinusoidale

Reprezentarea simbolica a marimilor sinusoidale

In cazul circuitelor electrice care au o structura mai complicata, determinarea regimului permanent prin metoda directa este foarte diferita si prea putin intuitiva. Din acest motiv se face apel la reprezentari simbolice pentru marimile sinusoidale care conduc la o rezolvare simpla a circuitelor. Prin reprezentari simbolice calculul circuitelor de curent alternativ devine tot atat de simplu ca si pentru circuitele de curent continuu.

Pentru ca rezolvarea simbolica sa fie eficienta, ea trebuie sa indeplineasca urmatoarele cerinte:

a) componenta sa fie biunivoca intre marimile sinusoidale si simboluri (adica fiecarei marimi sinusoidale sa-i corespunda un simbol si fiecarui simbol sa-i corespunda o marime sinusoidala si numai una);

b) transformarile directa si inversa sa se faca usor;

c) sa existe corespondenta operatiilor fundamentale;

d) calculele sa fie mai usor de efectuat;

e) circuitele sa fie liniare, iar marimile electrice reprezentate sa fie sinusoidale.

In studiul circuitelor de curent alternativ care functioneaza in regim permanent sinusoidal se utilizeaza doua tipuri de reprezentari simbolice:

a. reprezentarea geometrica:

- cinematica;

- polara;

b. reprezentarea analitica:

- in complex nesimplificata;

- in complex simplificata.

a. Reprezentarea geometrica

O reprezentare geometrica a unei marimi sinusoidale se bazeaza pe faptul ca o functie sinusoidala este caracterizata prin amplitudine (sau valoare efectiva) si faza, iar un vector liber in plan este caracterizat printr-un modul si argument.

Vectorul liber in plan se va numi in continuare fazor, pentru a se deosebi de vectorii din mecanica. Se introduce corespondenta biunivoca intre o marime sinusoidala (de exemplu, curentul) si fazorul corespunzator sub forma:

(6.76)

Reprezentarea geometrica cinematica (cu fazori rotitori)

In cazul acestei reprezentari (fig. 6.17), axa OX, fiind axa origine de faza, se roteste cu aceeasi viteza ω ca si fazorul . Axa de referinta OX₀ (axa observatorului) si axa transversala OY₀ raman fixe. Proiectia fazorului pe axa OY₀ este egala, in orice moment, cu valoarea instantanee a marimii sinusoidale i(t).

Vectorul , care se numeste fazor, nu reprezinta un curent electric, ci el este numai un simbol al curentului electric.

Se poate scrie corespondenta biunivoca intre marimea sinusoidala si fazorul astfel:

Si se exprima sub forma:

(6.77)

unde F(i) este fazorul curentului sinusoidal i(t) - un vector rotitor in sens trigonometric direct cu viteza ω.

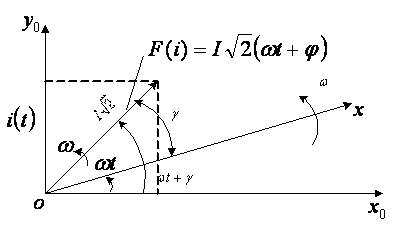
Fig.6.17

Aceasta reprezentare geometrica prin fazori este foarte sugestiva si intuitiva. Ea pune in evidenta amplitudinea marimii sinusoidale (egale cu modulul fazorului) precum si faza sa (egala cu argumentul fazorului reprezentativ).

Prin reprezentarea in acelasi plan a tensiunii si a curentului se poate pune in evidenta si unghiul de defazaj φ dintre aceste marimi (fig. 6.18). aceasta reprezentare poarta numele de "diagrama fazoriala".

Defazajul φ este pozitiv in sens trigonometric direct si negativ in sens invers.

Fig.6.18

Reprezentarea geometrica polara (cu fazori ficsi), (fig. 6.19)

Reprezentarea geometrica a marimilor sinusoidale se poate simplifica daca se renunta la marimile constante si ω. In aceste conditii ansamblul de vectori devine fix, toti fazorii aflandu-se in repaus relativ. Evident, este necesar ca toate marimile reprezentate in diagrama fazoriala sa aiba aceeasi frecventa.

Reprezentarea polara conserva din marimea sinusoidala numai elementele care o individualizeaza in raport cu celelalte marimi de aceeasi frecventa (valoarea efectiva si faza initiala).

Reprezentarea polara se exprima sub forma:

In construirea diagramei vectoriale una din marimile sinusoidale se ia ca origine de faza si se reprezinta printr-un vector orizontal orientat spre dreapta (de obicei curentul I). Celelalte marimi se reprezinta prin vectori rotiti in sens trigonometric daca sunt defazati inainte sau in sens orar cand sunt defazati in urma.

Fig.6.19.

b. Reprezentarea analitica.

Dupa cum se stie din algebra numerelor complexe, fiecarui numar complex ii corespunde biunivoc in planul complex al lui Gauss un punct (afixul numarului) si deci ii corespunde un vector de pozitie. Rezulta ca identificand planul reprezentarii geometrice cu planul complex, stabilim o corespondenta biunivoca intre functiile sinusoidale si numerele complexe. Asa cum in reprezentarea geometrica marimea sinusoidala se obtinea ca fiind proiectia fazorului reprezentativ pe axa transversala OY₀, la reprezentarea in complex marimea sinusoidala se obtine ca fiind partea imaginara a numarului complex reprezentativ (daca se identifica axa OX₀ cu axa reala OY₀ cu axa imaginara).

Identificand planul reprezentarii geometrice cu planul complex se poate trece la o noua corespondenta biunivoca:

(6.78)

numita "reprezentarea in complex" a marimii sinusoidale.

Dupa cum se va utiliza reprezentarea cinematica sau cea polara pentru identificarea cu planul complex, va rezulta:

reprezentarea in complex nesimplificata;

reprezentarea in complex simplificata.

Reprezentarea in complex nesimplificata se exprima prin relatia:

(6.79)

care arata ca imaginea in complex a marimii sinusoidale i(t) este o functie I complexa de modul egal cu amplitudinea marimii sinusoidale si de argument egal cu faza acestuia.

Transformarea inversa, respectiv determinarea valorii instantanee i(t) se obtine pe baza regulii trecerii inverse de la imagine la marimea sinusoidala:

(6.80)

si reprezinta partea imaginara a marimii complexe obtinute prin calcul.

Reprezentarea in complex simplificata - daca marimile sinusoidale au aceeasi frecventa, atunci se poate renunta la factorul comun si metoda reprezentarii in complex se poate simplifica rezultand reprezentarea in complex simplificata:

(6.81)

Aceasta relatie arata ca imaginea in complex a marimii sinusoidale i(t) este o functie complexa , de modul egal cu valoarea efectiva a marimii sinusoidale si de argument egal cu faza initiala a acestei marimi.

Regula trecerii inverse este in acest caz:

(6.82)

Metoda reprezentarii in complex simplificata este preferata in analiza circuitelor electrice.

C(i) se citeste "reprezentarea in complex a curentului";

este unitatea imaginara;

Imaginea in complex simplificat a unei marimi sinusoidale se noteaza cu simbolul subliniat al valorii efective ( etc.)

Defazajul a doua functiuni sinusoidale:

Imaginea unei derivate:

Imaginea unei integrale:

Imaginile in complex simplificat ale marimilor sinusoidale se reprezinta in planul complex prin vectori ficsi, care formeaza cu axa reala un unghi egal cu faza initiala a marimii sinusoidale. Constructia diagramei vectoriale se face tinand seama ca inmultirea cu j inseamna rotirea fazorului in sens trigonometric cu , iar impartirea cu j inseamna rotirea fazorului in sens orar cu

Corespondenta operatiilor elementare

Operatiilor elementare cu marimi sinusoidale le corespund operatii algebrice elementare cu imagini in complex, precum si operatii cu fazori in planul complex.

a)    Adunarea marimilor sinusoidale corespunde biunivoc cu adunarea imaginilor in complex, precum si cu adunarea vectoriala a fazorilor corespunzatori acestor marimi. Suma a doua marimi sinusoidale va fi tot o marime sinusoidala de aceeasi frecventa:

(6.83)

(6.83.a)

(6.84)

(6.84.a)

b)    Amplificarea cu o constanta

Amplificarea cu un scalar a marimilor sinusoidale corespunde biunivoc cu amplificarea cu acel scalar a imaginilor in complex, respective a fazorilor marimilor respective.

(6.85)

Operatiile de adunare si amplificare cu un factor constant exprima caracterul liniar al reprezentarilor simbolice.

c)    Derivarea

Derivata unei marimi sinusoidale este tot o marime sinusoidala defazata cu inainte fata de marimea primitiva si avand amplitudinea de ω ori mai mare.

(6.86)

Derivarea in raport cu timpul a unei marimi sinusoidale corespunde biunivoc ca rotirea in sens trigonometric direct a fazorului respectiv amplificat cu pulsatia ω, respectiv cu inmultirea cu jω a imaginea in complex a marimii respective.

(6.87)

(6.87.a)

d)    Integrarea

Integrala unei marimi sinusoidale este tot o marime sinusoidala defazata cu in urma marimii primitive si avand amplitudinea de ω ori mai mica.

(6.88)

Integrarea in raport cu timpul a unei marimi sinusoidale corespunde biunivoc cu rotirea in sens invers a fazorului corespunzator amplificat cu valoarea reciproca a pulsatiei , respectiv cu impartirea prin a imaginii in complex a marimii respective.

(6.89)

(6.89')

Aplicatie

A.    Rezolvarea circuitului serie R, L, C utilizand reprezentarea fazoriala a marimilor sinusoidale .

Fig.6.20

Ecuatia circuitului este:

(6.90)

Se cere sa se determine curentul, cunoscand parametrii R, L, C si tensiunea aplicata u(t). Curentul din circuit (fiind sinusoidal si de aceeasi forma cu tensiunea aplicata) este caracterizat prin valoarea sa efectiva I si prin defazajul sau φ fata de tensiune. Expresia curentului, conform metodei directe, are forma:

(6.91)

Considerand curentul ca origine de faza se construieste (fig. 6.21) suma fazoriala corespunzatoare membrului drept al relatiei (6.90), tinand cont de corespondenta operatorilor stabilita mai sus.

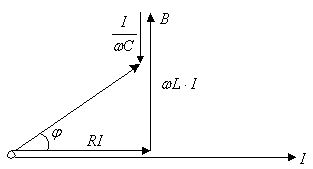
Fig.6.21

Suma din membrul drept trebuie sa fie egala cu tensiunea aplicata (poligonul se inchide). Din triunghiul dreptunghic OAB se deduce:

(6.92)

de unde:

(6.93)

Apoi:

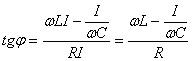(6.94)

de unde:

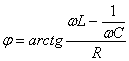(6.95)

Relatiile (6.93) si (6.95) au rezolvat problema pusa.

B.    Rezolvarea aceluiasi circuit serie R, L, C (fig. 6.20) prin reprezentarea in complex a marimilor sinusoidale.

Deoarece adunarii si amplificarii marimilor sinusoidale le corespund adunarea si amplificarea imaginilor complexe, respectiv a fazorilor, ecuatia (6.90) va avea ca imagine relatia:

(6.96)

Ecuatia (6.96) este reprezentata in planul complex prin diagrama din figura (6.22), care, dupa cum se vede, este identica cu diagrama fazoriala din figura (6.71)

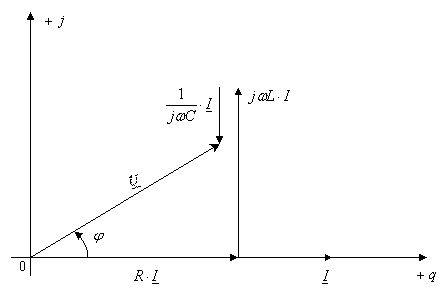
Fig.6.22.

Rezolvarea ecuatiei (6.96) conduce la:

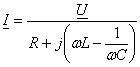(6.97)

cu

(6.98)

si

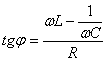(6.99)