Miscarea relativa a punctului

MISCAREA RELATIVA A PUNCTULUI

1.1. DERIVATA ABSOLUTA SI RELATIVA A UNUI VECTOR

Se considera sistemul de referinta fix O₁x₁y₁z₁, de versori si sistemul de referinta mobil Oxyz, de versori precum si un vector care poate fi scris prin proiectii pe cele doua sisteme de axe, astfel:

(1)

Derivând în raport cu timpul, relatia (1), obtinem:

(2)

Termenul din membrul stâng al egalitatii (2) reprezinta derivata în raport cu timpul a vectorului , exprimat prin proiectii pe axele sistemului de referinta fix si se numeste derivata absoluta:

(3)

Prima paranteza din membrul drept reprezinta derivata în raport cu timpul a vectorului , exprimat prin proiectii pe axele sistemului de referinta mobil, ca si când acesta ar fi fix (versorii nu-si modifica directia) si se numeste derivata locala sau derivata relativa:

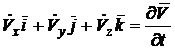(4)

Introducând relatiile Poisson (9.12) în paranteza a doua din membrul drept al relatiei (2), rezulta:

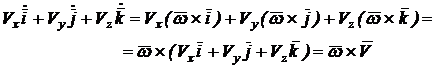(5)

Tinând seama de relatiile (3), (4) si (5), relatia (2) devine:

(6)

si exprima derivata absoluta a unui vector definit prin proiectiile sale pe axele triedrului mobil.

1.2. DEFINIREA MISCARILOR

Se considera un sistem de referinta fix           O₁x₁y₁z₁, de versori si un sistem de referinta mobil Oxyz, de versori . Pozitia unui punct M în raport cu triedrul fix este definita de vectorul de pozitie , în raport cu triedrul mobil, de vectorul de pozitie , pozitia triedrului mobil în raport cu triedrul fix fiind definita de vectorul de pozitie (fig.1).

Miscarea absoluta este miscarea punctului în raport cu reperul fix.

Miscarea relativa este miscarea punctului în raport cu reperul mobil.

Miscarea de transport este miscarea punctului solidar cu reperul mobil, din miscarea acestuia în raport cu triedrul fix. Sistemul de referinta mobil se mai numeste si transportor.

Vitezele si acceleratiile punctului din miscarile definite mai sus se numesc: viteza absoluta, viteza relativa si viteza de transport, respectiv, acceleratie absoluta, acceleratie relativa si acceleratie de transport.

Viteza si acceleratia de transport sunt date de relatiile (9.14) si (9.22), cunoscute din studiul miscarii rigidului:

(7)

1.3. COMPUNERA VITEZELOR

Relatia dintre vectorii ce exprima pozitia punctului M, în raport cu cele doua sisteme de referinta este:

(8)

Derivând aceasta relatie în raport cu timpul, obtinem:

(9)

Având în vedere ca reprezinta viteza originii tredrului mobil din miscarea fata de triedrul fix si ca vectorul este definit prin proiectiile sale pe axele triedrului mobil, deci i se aplica regula de derivare (6), se obtine:

(10)

unde:

reprezinta viteza punctului M, în raport cu triedrul fix si se numeste viteza absoluta;

reprezinta viteza punctului M, în raport cu triedrul mobil si se numeste viteza relativa;

reprezinta viteza punctului M, solidar cu triedrul mobil (transportorul), din miscarea acestuia în raport cu triedrul fix si se numeste viteza de transport.

Cu aceste notatii, relatia (10) devine:

(11)

adica: viteza absoluta a unui punct este egala cu suma vectoriala dintre viteza relativa si viteza de transport a punctului.

1.4. COMPUNEREA ACCELERATIILOR

Derivând în raport cu timpul, relatia (10) si având în vedere ca reprezinta acceleratia originii tredrului mobil din miscarea fata de triedrul fix, , vectorii si sunt definiti prin componentele lor pe axele triedrului mobil, deci li se aplica regula de derivare (6), se obtine:

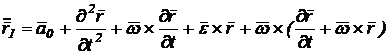(12)

Grupând convenabil termenii se poate scrie:

(13)

unde:

reprezinta acceleratia punctului M, în raport cu triedrul fix si se numeste acceleratie absoluta;

reprezinta acceleratia punctului M, în raport cu triedrul mobil si se numeste acceleratie relativa;

reprezinta acceleratia punctului M, solidar cu triedrul mobil (transportorul), din miscarea acestuia în raport cu triedrul fix si se numeste acceleratie de transport;

reprezinta o acceleratie ce nu apartine vreunei miscari; exprima influenta simultana a miscarii de rotatie a sistemului mobil si a miscarii relative a punctului asupra acceleratiei absolute, numidu-se acceleratie complementara sau acceleratie Coriolis.

Cu aceste notatii, relatia (13) devine:

(14)

adica: acceleratia absoluta a unui punct este egala cu suma vectoriala dintre acceleratia relativa acceleratia de transport si acceleratia Coriolis a punctului.

Observatie: Conform definitiei, acceleratia Coriolis este produsul vectorial al vectorilor si , 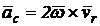. Aceasta acceleratie devine nula, când:

, adica triedrul mobil executa o miscare de translatie în raport cu triedrul fix;

, vectorul ramâne în permanenta paralel cu vectorul .