REDUCEREA SISTEMELOR DE FORTE

1 Generalitati asupra fortelor

1.1 Efectul mecanic al fortei

Din punctul de vedere al Mecanicii efectul unei forte se poate evalua prin miscarea sau tendinta de miscare pe care aceasta o impune. Aplicata unui punct material ea va determina o translatie dupa directia si în sensul ei de actiune. Aplicata unui corp solid rigid, pe lânga translatie, forta va determina si o rotatie în jurul unui punct sau al unei axe.

Legat de acest aspect trebuie mentionat caracterul de vector alunecator al fortei. Astfel, o forta aplicata într-un punct al unui corp (fig. 1) poate fi deplasata pe suportul ei într-un alt punct al corpului, fara ca prin aceasta efectul asupra corpului sa se modifice.

1.2 Definirea analitica a fortei

Pornind de la relatiile generale (2.3), proiectiile unei forte oarecare pe axele de coordonate ale unui sistem de referinta cartezian sunt:

(1)

în care a b g sunt unghiurile directoare ale suportului fortei (fig. 2.4). n conformitate cu rel. (2.6), aceleasi proiectii mai pot fi calculate si cu relatiile:

(2)

Unghiurile q si y au semnificatiile din fig.2.5. Expresia analitica a fortei este:

(3)

Daca o forta este coliniara cu un segment de dreapta marginit de punctele A si B (fig. 2), proiectiile fortei se pot calcula si în functie de coordonatele acestora, observând asemanarea cu proiectiile segmentului AB:

(4)

Lungimea segmentului AB în functie de coordonate este:

(5)

1.3 Momentul unei forte fata de un punct

Capacitatea fortei de a roti corpul asupra caruia este aplicata în jurul unui punct se evalueaza prin momentul fortei fata de punctul respectiv. Momentul se defineste vectorial prin relatia

(6)

în care reprezinta vectorul de pozitie al punctului de aplicatie al fortei în raport cu punctul fata de care se calculeaza momentul, în cazul de fata O (fig. 3). Cu referire la cele aratate anterior referitor la produsul vectorial, pentru momentul fortei se poate scrie

(7)

Perpendiculara dusa din punctul de calcul al momentului pe directia fortei reprezinta bratul fortei fata de punctul O.

Directia vectorului este perpendiculara pe planul format de vectorii si iar sensul se stabileste prin regula surubului drept care, în cazul de fata corespunde sensului în care forta tinde sa roteasca corpul.

Cu expresiile analitice ale vectorilor în sistemul de referinta cartezian, momentul ia forma:

(8)

careia îi corespunde determinantul

(9)

Din dezvoltarea rezulta proiectiile:

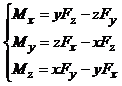(10)

Referitor la momentul fortei fata de un punct se evidentiaza proprietatile:

a) Momentul nu se modifica daca forta aluneca pe suportul ei de actiune (fig.4). Astfel:

(11)

deoarece , vectorii fiind coliniari. Se confirma caracterul de vector alunecator al fortei afirmat mai înainte.

b) Momentul se modifica la schimbarea punctului fata de care se face calculul (fig. 5):

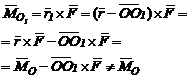(12)

deoarece produsul este în general diferit de 0; se spune ca momentul unei forte este un vector legat de punctul de calcul.

c) momentul este nul daca sau este coliniar cu ceea ce exprima faptul ca o forta nu poate roti corpul în jurul punctului ei de aplicatie sau în jurul unui punct aflat pe directia ei de actiune.

1.4 Momentul unei forte fata de o axa

Momentul fata de o axa exprima capacitatea fortei de a roti corpul în jurul axei respective. Acest moment se defineste prin proiectia pe directia axei a vectorului momentului fortei calculat în raport cu un punct oarecare de pe axa. Astfel, cu referire la fig.6,

(13)

Spre deosebire de momentul fata de un punct, momentul fata de o axa este, o marime scalara. În cazul în care forta si axa sunt coplanare atunci momentul fata de aceasta axa este nul (cap.2.4.4). Concret, daca forta este coliniara, paralela sau concurenta cu axa, ea nu va putea roti corpul în jurul acesteia (fig. 7).

Trebuie remarcat faptul ca în relatia de definire analitica a momentului unei forte fata de originea O a unui sistem de coordonate cartezian (fig.8), respectiv

, (14)

proiectiile pe axe ale vectorului reprezinta chiar momentele acestei forte fata de axele de coordonate Ox, Oy si Oz, deoarece punctul O apartine simultan celor trei axe.

1.5 Teorema momentelor

Sistemul de forte concurente aplicat din punctul A (fig.9) are rezultanta:

(15)

Se înmulteste aceasta relatie vectorial la stânga cu vectorul de pozitie al punctului A fata de un punct O. Se obtine:

(16)

Se înmulteste scalar aceasta relatie cu versorul al unei axe care trece prin O:

Tinând cont de (13) relatia devine 

(17)

Relatiile (16) si (17) exprima teorema momentelor, respectiv faptul ca momentul în raport cu un punct sau o axa al rezultantei unui sistem de forte concurente este egal cu suma momentelor acestor forte fata de punctul sau axa respectiva.

În practica, aceasta teorema permite calcularea cu mai multa usurinta a momentului unei forte fata de un punct sau o axa printr-o descompunere convenabila a fortei în componente.

1.6 Cuplul de forte

Prin cuplu de forte se întelege un ansamblu de doua forte paralele, egale si de sens contrar (fig. 10). Cuplul, notat , are ca efect rotirea corpului asupra caruia actioneaza în jurul unei axe oarecare, perpendiculara pe planul format de cele doua forte.

Se pot pune în evidenta urmatoarele proprietati :

a) Proiectia unui cuplu de forte pe orice axa este nula. Facând, de exemplu, proiectarea pe directia D (fig. 11) rezulta:

(18)

b) Momentul unui cuplu de forte are aceeasi valoare oricare ar fi punctul de calcul. Cu notatiile din fig. 12 se poate scrie:

(19)

Se constata ca momentul cuplului depinde doar de distanta dintre suporturile fortelor; pozitia punctului O nu intervine în relatia de mai sus, acesta putând fi oriunde în spatiu. Spre deosebire de momentul unei singure forte, momentul unui cuplu este un vector liber.

2 Reducerea fortelor concurente

2.1   Generalitati

În cazul unui sistem de forte având toate acelasi punct de aplicatie, operatiunea de reducere consta în gasirea unei singure forte aplicata în punctul respectiv, echivalenta ca efect sistemului dat. Este evident ca aceasta forta este tocmai rezultanta sistemului.

Daca sistemul de forte mentionat este aplicat unui punct material, efectul acestuia va consta în deplasarea punctul pe directia si în sensul de actiune al rezultantei.

Metodele pentru calculul rezultantei fortelor concurente, atât pe cale grafica cât si analitica, sunt cele analizate în cap.2 pentru sistemele de vectori concurenti.