Grafuri

1 Definitie si moduri de reprezentare

Un graf este o pereche ordonata , unde este o multime finita de noduri, iar este multimea arcelor intre noduri. In continuare vom nota cu numarul de noduri si cu numarul de arce din graf.

Exista doua tipuri de grafuri:

• orientate: este un arc dirijat de la nodul la nodul ; in acest caz, nodul se numeste predecesorul nodului in graf;
• neorientate: si reprezinta acelasi arc intre nodurile si

Pentru fiecare nod din graf se defineste multimea nodurilor adiacente ca multimea nodurilor direct accesibile din :

Pentru rezolvarea problemelor economice, in general, nodurilor si arcelor grafului se ataseaza informatii suplimentare necesare implementarii algoritmilor specifici grafurilor sau rezolvarii problemelor specifice. Pentru algoritmii specifici, cele mai importante informatii sunt costurile asociate muchiilor grafului, notate cu . Grafurile care au costuri asociate nodurilor se numesc grafuri ponderate.

Pentru reprezentarea grafurilor exista doua metode importante: matrice de adiacenta si liste de adiacenta.

Pentru exemplificare vom considera graful orientat ponderat din figura 1.

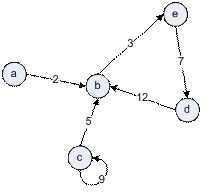
Fig. 1: Graf orientat ponderat

Prima metoda de reprezentare presupune construirea unei matrice patratice de dimensiune , unde:

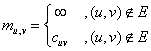
Matricea corespunzatoare grafului din figura 1 este:

In cazul reprezentarii prin liste de adiacenta se vor construi liste care vor contine multimile . Pentru exemplul considerat, reprezentarea prin liste de adiacenta va fi:

Cele doua moduri de reprezentare pot fi folosite similar si in cazul grafurilor neorientate, dupa cum se poate observa din figura urmatoare:

Fig. 2: Reprezentare graf neorientat

Modul de reprezentare se alege in functie de caracteristicile datelor folosite si de algoritmii aplicati asupra grafului. Reprezentarea prin matrice de adiacenta are avantajul accesarii rapide a informatiilor legate de muchii, insa poate consuma inutil o mare cantitate de memorie in cazul in care . In cazul in care numarul de arce este apropiat de se va folosi reprezentarea prin matrice de adiacenta, iar in cazul in care numarul arcelor este mic se va folosi reprezentarea prin liste de adiacenta.

Trebuie observat faptul ca cele doua moduri de reprezentare sunt echivalente din punctul de vedere al informatiilor continute si a operatiilor permise. Diferentele intre cele doua tin exclusiv de performante.

2 Construirea grafurilor

Pentru simplificarea implementarii vom face urmatoarele conventia ca multimea in cazul unui graf cu n noduri va fi de forma .

Avand in vedere faptul ca operatiile de baza sunt comune pentru ambele tipuri de reprezentare, vom grupa declaratiile operatiilor intr-o clasa de baza abstracta numita Graf. Implementarea operatiilor tinand cont de particularitatile celor doua metode de reprezentare va fi realizata in doua clase concrete GrafMatrice si GrafListe. Figura 3 prezinta aceasta ierarhie.

Fig. 3: Ierarhia claselor

Aceasta abordare permite construirea de algoritmi de prelucrare a grafurilor aplicabili pentru ambele tipuri de reprezentare. Utilizatorul va putea alege pentru fiecare problema in parte modalitatea optima de reprezentare, fara a fi nevoit sa rescrie algoritmii de prelucrare.

Declaratia folosita pentru clasa Graf este:

class Graf

// constructor implicit

Graf(Graf&) // constructor de copiere

// Operatii noduri

virtual int AdaugaNod() = 0;

virtual void StergeNod(int nod) = 0;

virtual int NumarNoduri() = 0;

// Operatii muchii

// ----- ----- -----

virtual void AdaugaMuchie(int sursa, int destinatie, int cost = 1) = 0;

virtual void StergeMuchie(int sursa, int destinatie) = 0;

virtual bool ExistaMuchie(int sursa, int destinatie) = 0;

virtual int ValoareMuchie(int sursa, int destinatie) = 0;

virtual list<int> NoduriAdiacente(int nodSursa) = 0;

// Operatii diverse

// ----- ----- ------

virtual bool EOrientat() = 0;

// Constante

// ---------

static const int INFINIT = 100000;

static const int NOD_INEXISTENT = -1;

Pentru a asigura o compatibilitate intre diversele implementari ale clasei prezentam in continuare descrierea operatiilor de baza prezentate:

Tabelul 1: Descrierea operatiilor de baza

Pentru reprezentarea sub forma de matrice de adiacenta s-a folosit clasa vector din biblioteca standard. Matricea de adiacenta este declarata ca vector de vectori. Aceasta implementare permite accesul direct la informatiile referitoare la muchii si redimensionarea matricei pentru adaugarea/stergerea de noduri.

Declaratia folosita pentru clasa GrafMatrice este

class GrafMatrice : public Graf

// constructor implicit

// Operatii noduri

// ----- ----- -----

virtual int AdaugaNod();

virtual void StergeNod(int nod);

virtual int NumarNoduri();

// Operatii muchii

// ----- ----- -----

virtual void AdaugaMuchie(int sursa, int destinatie, int cost = 1);

virtual void StergeMuchie(int sursa, int destinatie);

virtual bool ExistaMuchie(int sursa, int destinatie);

virtual int ValoareMuchie(int sursa, int destinatie);

virtual list<int> NoduriAdiacente(int nodSursa);

// Operatii diverse

// ----- ----- ------

virtual bool EOrientat();

private: // *** Membri privati ***

bool orientat;

vector< vector<int> > matriceAdiacenta;

Constructorul clasei permite specificarea numarului initial de noduri si a tipului grafului. Implementarea operatiilor s-a facut respectand specificatiile prezentate anterior.

Codul sursa comentat folosit pentru implementarea operatiilor este:

// Constructori

// Intializeaza o instanta a grafului.

GrafMatrice::GrafMatrice(int numarNoduri, bool orientat)

// constructor de copiere

GrafMatrice::GrafMatrice(GrafMatrice& graf)

// Operatii noduri

int GrafMatrice::AdaugaNod()

void GrafMatrice::StergeNod(int nod)

int GrafMatrice::NumarNoduri()

// Operatii muchii

void GrafMatrice::AdaugaMuchie(int sursa, int destinatie, int cost)

void GrafMatrice::StergeMuchie(int sursa, int destinatie)

bool GrafMatrice::ExistaMuchie(int sursa, int destinatie)

int GrafMatrice::ValoareMuchie(int sursa, int destinatie)

list<int> GrafMatrice::NoduriAdiacente(int nodSursa)

// Operatii diverse

bool GrafMatrice::EOrientat()

Pentru cea de-a doua modalitate de reprezentare s-a ales utilizarea unei structuri de date compuse dintr-un vector de liste. Aceasta abordare necesita mai multe resurse pentru adaugarea/stergerea unui nod, dar permite accesul direct la listele de adiacenta (operatie mult mai frecventa in cadrul algoritmilor de prelucrare).

Listele de adiacenta contin perechi de forma (cod_nod, cost_muchie), cu semnificatiile prezentate in sectiunea 1.

Declaratia clasei GrafListe este:

class GrafListe : public Graf

// contructor implicit

// Operatii noduri

// ----- ----- -----

virtual int AdaugaNod();

virtual void StergeNod(int nod);

virtual int NumarNoduri();

// Operatii muchii

// ----- ----- -----

virtual void AdaugaMuchie(int sursa, int destinatie, int cost = 1);

virtual void StergeMuchie(int sursa, int destinatie);

virtual bool ExistaMuchie(int sursa, int destinatie);

virtual int ValoareMuchie(int sursa, int destinatie);

virtual list<int> NoduriAdiacente(int nodSursa);

// Operatii diverse

// ----- ----- ------

virtual bool EOrientat();

private: // *** Membri privati ***

// cauta un nod intr-o lista de

// adiacenta

list< pair<int,int> >::iterator CautaNod(list< pair<int,int> >& lista, int nod);

bool orientat;

vector< list< pair<int,int> > > listeAdiacenta;

In plus fata de operatiile standard a fost inclusa o functie ajutatoare privata numita CautaNod, folosita pentru determinarea pozitiei unui nod intr-o lista de adiacenta.

Implementarea metodelor clasei este:

// Constructori

// Intializeaza o instanta a grafului.

GrafListe::GrafListe(int numarNoduri, bool orientat)

// constructor de copiere

GrafListe::GrafListe(GrafListe& graf)

// Operatii noduri

int GrafListe::AdaugaNod()

void GrafListe::StergeNod(int nod)

}

// sterge lista de adiacenta corespunzatoare

// nodului de sters

listeAdiacenta.erase(

listeAdiacenta.begin() + (size_t)nod);

int GrafListe::NumarNoduri()

// Operatii muchii

void GrafListe::AdaugaMuchie(int sursa, int destinatie, int cost)

void GrafListe::StergeMuchie(int sursa, int destinatie)

bool GrafListe::ExistaMuchie(int sursa, int destinatie)

int GrafListe::ValoareMuchie(int sursa, int destinatie)

list<int> GrafListe::NoduriAdiacente(int nodSursa)

// Operatii diverse

bool GrafListe::EOrientat()

// cauta un nod intr-o lista de

// adiacenta

list< pair<int,int> >::iterator GrafListe::CautaNod(list< pair<int,int> >& lista, int nod)

Pentru exemplificarea modului de utilizare a claselor pentru construirea grafurilor prezentam codul sursa corespunzator figurilor 1 si 2.

// Figura 1: Graf orientat

// declarare graf sub forma de

// matrice de adiacenta

GrafMatrice graf_11_1(5, true);

// adaugarea muchiilor si a costurilor aferente

graf_11_1.AdaugaMuchie(0, 1, 2); // pt. a--2-->b

graf_11_1.AdaugaMuchie(1, 4, 3);

graf_11_1.AdaugaMuchie(2, 1, 5);

graf_11_1.AdaugaMuchie(2, 2, 9);

graf_11_1.AdaugaMuchie(3, 1, 12);

graf_11_1.AdaugaMuchie(4, 3, 7);

// Figura 2: Graf neorientat

// declarare graf neorientat sub

// forma de liste de adiacenta

GrafListe graf_11_2(5, false);

// adaugarea muchiilor (muchiile

// inverse sunt adaugate automat

// datorita faptului ca graful

// este neorientat)

graf_11_2.AdaugaMuchie(0, 1, 2);

graf_11_2.AdaugaMuchie(1, 4, 3);

graf_11_2.AdaugaMuchie(2, 1, 5);

graf_11_2.AdaugaMuchie(3, 1, 12);

graf_11_2.AdaugaMuchie(4, 3, 7);

Pentru afisarea grafurilor astfel create putem folosi functia urmatoare:

void AfisareGraf(Graf& g)

cout << endl;

}

Functia AfisareGraf permite afisarea informatiilor complete despre graf. Ea poate fi folosita pentru orice graf, indiferent de tip (orientat/neorientat) si mod de reprezentare (matrice/liste de adiacenta). Apelurile necesare pentru afisarea grafurilor prezentate sunt:

AfisareGraf(graf_11_1);

AfisareGraf(graf_11_2);

Problema 1

Se considera doua grafuri de acelasi tip (orientate/neorientate). Se cere sa se scrie functia de concatenare a acestora.

Rezolvare

Functia va primi ca date de intrare vor fi cele doua grafuri si va returna prin intermediul unui parametru de iesire noul graf care va contine concatenarea acestora. Concatenarea se va face prin crearea unui nou graf si adaugarea nodurilor si legaturilor grafurilor initiale la acesta.  Se va tine cont de proprietatile specificate pentru functiile de adaugare nod.

void ConcatenareGrafuri(

// param de intrare

Graf& graf1, Graf& graf2,

// param de iesire (graful concatenat)

Graf& rezultat)

// repetam procesul pentru cel de-al doilea

// graf tinand cont de proprietatile grafului

// adaugam nodurile

for (i = 0; i < nr2; i++)

rezultat.AdaugaNod();

// adaugam muchiile

for (i = 0; i < nr2; i++)

3 Stocarea grafurilor in fisiere

Pentru stocarea grafurilor in fisiere s-au folosit facilitatile oferite de limbajul C++: stream-uri si supraincarcarea operatorilor.

Pentru clasele GrafMatrice si GrafListe au fost definiti operatorii >> si << pentru citirea/scrierea datelor in/din stream-uri. Acesti operatori pot fi folositi pentru scrierea/citirea datelor in fisiere, zone de memorie sau consola. Formatul ales este unul de tip text deoarece permite o modificare usoara a informatiilor stocate folosind un editor simplu si permite importarea usoara in alte aplicatii pentru prelucrari ulterioare.

Pentru GrafMatrice formatul folosit este

Implementarea operatorilor de citire/scriere este:

// Operatori I/E

ostream& operator << (ostream& fisier, GrafMatrice& graf)

// intoarcem referinta la fisier

return fisier;

istream& operator >> (istream& fisier, GrafMatrice& graf)

Pentru clasa MatriceListe, formatul fisierelor folosite este:

Unde:

N - numarul de noduri din graf

dimI - numarul de noduri accesibile din nodul I

Implementarea operatorilor de citire/scriere este:

// Operatori I/E

ostream& operator << (ostream& fisier, GrafListe& graf)

// intoarcem referinta la fisier

return fisier;

istream& operator >> (istream& fisier, GrafListe& graf)

}

return fisier;

In afara datelor salvate de catre clasa arbore, in fisier pot fi introduse si alte date specifice problemei de rezolvat (date asociate nodurilor, muchiilor, .).

Folosirea operatorilor urmeaza modelul claselor din biblioteca standard. De exemplu, pentru salvarea si citirea grafurilor create anterior se pot folosi secventele:

// salvare graf 1 ca matrice

ofstream fisier('graf_11_1.txt');

fisier << graf_11_1;

// restaurare graf 1 (salvat anterior ca matrice)

GrafMatrice graf;

ifstream fisier('graf_11_1.txt');

fisier >> graf;

// salvare graf 2 ca liste

ofstream fisier('graf_11_2.txt');

fisier << graf_11_1;

// restaurare graf 2 (salvat anterior ca liste)

GrafListe graf;

ifstream fisier('graf_11_2.txt');

fisier >> graf;

4 Parcurgerea in latime

Parcurgerea in latime este unul dintre cei mai simpli algoritmi de parcurgere pentru un graf. Strategia folosita de aceasta parcurgere sta la baza mai multor algoritmi importanti din teoria grafurilor

Pornind de la un nod sursa s, algoritmul parcurge sistematic graful pentru a descoperi toate nodurile accesibile din nodul sursa. Rezultatul consta intr-un un arbore cu radacina in s care contine toate nodurile accesibile pornind de la acesta. De asemenea, sunt calculate si distantele minime (ca numar de muchii) de la nodul sursa la toate celelalte noduri accesibile.

Nodurile arborelui se pot afla in una dintre cele trei stari nevizitat (Alb), vizitat (Cenusiu) sau procesat (Negru). Pentru parcurgerea grafului se foloseste o coada care contine nodurile de prelucrat. Initial, coada contine doar nodul sursa. La fiecare pas al algoritmului se extrage un nod din coada. Se identifica toate nodurile adiacente si se adauga in coada, iar nodul curent este marcat ca procesat.

Algoritmul porneste de la un nod sursa specificat. La fiecare pas sunt identificate si adaugate in coada de procesare nodurile adiacente nevizitate inca. La adaugarea nodului in coada se seteaza culoarea acestuia pe Cenusiu si se seteaza distanta si predecesorul. Algoritmul se opreste in momentul in care se epuizeaza coada de procesare.

Pentru graful din figura 1, rezultatele intermediare obtinute in urma aplicarii algoritmului sunt:

Figura 4: Parcurgerea in adancime

Codul care implementeaza algoritmul este:

enum CuloriGraf // starea nodului

void ParcurgereLatime(Graf& g, int sursa, vector<int>& distante, vector<int>& predecesori)

// stergem nodul procesat din coada

coada.pop();

culori[nodCurent] = Negru;

}

Algoritmul este util pentru a determina toate nodurile accesibile dintr-un nod sursa, precum si distantele si drumurile minime de la acesta pana la celelalte noduri accesibile ale grafului.

Problema 2

Se considera un graf neorientat stocat intr-un fisier. Dandu-se un nod sursa se cere sa se determine toate nodurile accesibile si drumurile minime (ca numar de muchii) catre acestea.

Rezolvare

Pentru rezolvarea problemei vom folosi informatiile obtinute prin parcurgerea in latime a grafului pornind din nodul sursa specificat. Drumurile corespunzatoare distantelor minime se pot obtine recursiv pe baza vectorului de predecesori.

Codul sursa complet:

#include <iostream>

#include <fstream>

using namespace std;

#include 'Graf.h'

#include 'GrafAlgoritmi.h'

#include 'GrafListe.h'

// refacem si afisam recursiv drumul

// pe baza informatiilor obtinute din parcurgerea

// in latime

void AfisareDrum(vector<int>& predecesori, int sursa, int destinatia)

}

void main()

5 Parcurgerea in adancime

Parcurgerea in adancime este unul dintre cei mai importanti algoritmi din teoria grafurilor. Informatiile obtinute prin aceasta parcurgere pot fi folosite pentru a determina cele mai multe din proprietatile unui graf.

Rezultatul obtinut in urma parcurgerii in adancime este o padure de arbori corespunzatori componentelor conectate ale grafului.

Algoritmul foloseste aceeasi tehnica de marcare a nodurilor ca si parcurgerea in latime. Diferenta este ca nodurile sunt explorate incepand cu ultimul nod selectat (asemanator explorarii labirintului). In figura 5 pot fi observati pasii urmati de catre algoritm.

Figura 5: Parcurgerea in adancime

In timpul parcurgerii, este retinut intr-o variabila un contor de timp care este incrementat la fiecare operatie. Pentru fiecare nod se retin timpii de inceput (momentul in care nodul a fost descoperit) si de sfarsit (momentul in care toti descendentii au fost procesati), precum si predecesorul sau.

Implementarea in C++ a algoritmului folosind clasa graf creata anterior este:

void ExplorareNod(Graf& g, int& timp, int nod,

vector<int>& tInceput, vector<int>& tSfarsit,

vector<int>& predecesori, vector<CuloriGraf>& culori);

void ParcurgereAdancime(Graf& g,

vector<int>& tInceput, vector<int>& tSfarsit,

vector<int>& predecesori)

void ExplorareNod(Graf& g, int& timp, int nod,

vector<int>& tInceput, vector<int>& tSfarsit,

vector<int>& predecesori, vector<CuloriGraf>& culori)

// marcam nodul ca procesat

culori[nod] = Negru;

// si inregistram momentul incheierii

// explorarii subgrafului corespunzator

timp++;

tSfarsit[nod] = timp;

Parcurgerea in adancime are o importanta deosebita in teoria grafurilor deoarece strategia folosita sta la baza multor algoritmi fundamentali si furnizeaza informatii despre graf utile in rezolvarea problemelor de ordin practic.

Problema 2

Se considera un graf memorat intr-un fisier sub forma de matrice de adiacenta. Se cere sa se efectueze parcurgerea in adancime a grafului si afisarea informatiilor obtinute.

Rezolvare

Graful va fi citit din fisier folosind operatorii de intrare/iesire prezentati in sectiunea 3. In urma parcurgerii in adancime vom afisa pentru fiecare nod timpii de inceput si sfarsit, precum si drumul pana la radacina arborelui corespunzator.

Codul sursa complet:

#include <iostream>

#include <fstream>

using namespace std;

#include 'Graf.h'

#include 'GrafMatrice.h'

#include 'GrafAlgoritmi.h'

// numele fisierului care contine graful

const char* const numeFisier = 'm_adancime.txt';

void main()

cout << endl;

}

6 Sortarea topologica

Sortarea topologica a unui graf orientat presupune gasirea unei ordonari a nodurilor astfel incat daca arborele contine o muchie (i,j), atunci i se va afla inaintea lui j in lista. In general, solutia nu este unica pentru aceasta trebuie impuse conditii suplimentare.

Pentru realizarea sortarii topologice se pot folosi informatiile obtinute in urma parcurgerii in adancime a grafului. Se poate demonstra (vezi [CLR90]) ca, pentru oricare noduri i si j, daca exista o muchie (i,j), atunci timpul de sfarsit al lui i este mai mic decat al lui j. In concluzie, pentru a obtine o sortare topologica a grafurilor este suficient sa inseram nodurile in lista in ordinea timpilor de terminare.

Codul C++ pentru realizarea sortarii topologice pe baza informatiilor furnizate de parcurgerea in adancime este:

vector<int> SortareTopologica(Graf& g, vector<int>& tSfarsit)

vector<int> noduri = vector<int>(g.NumarNoduri());

for (int i = 0; i < g.NumarNoduri(); i++)

return noduri;

Sortarea topologica are multe aplicatii practice in domenii ca planificarea activitatilor, proiectarea circuitelor logice sau proiectarea compilatoarelor.

Problema 4

Se considera un proiect constituit dintr-o multime de activitati. Pentru fiecare activitate se cunoaste lista activitatilor de care depinde in mod direct. Se cere sa se gaseasca o ordonare a activitatilor astfel fiecare activitate sa fie planificata dupa activitatile de care depinde.

Rezolvare

Pentru rezolvarea problemei vom construi un graf orientat in care vom reprezenta activitatile sub forma de noduri si dependintele sub forma de muchii intre activitati.

Functia de citire construieste un vector pentru denumirile activitatilor. Dependintele sunt furnizate de catre utilizator sub forma de perechi (activitate independenta, activitate dependenta) si sunt translatate de catre functie in muchii de graf.

Ordonarea activitatilor se face sortand topologic graful pe baza informatiilor furnizate de parcurgerea in adancime.

Codul sursa C++ este:

#include <iostream>

#include <vector>

#include <string>

#include <algorithm>

using namespace std;

#include 'Graf.h'

#include 'GrafMatrice.h'

#include 'GrafAlgoritmi.h'

// Functia pentru citirea datelor de intrare

// Memoreaza denumirile activitatilor intr-un vector

// si dependintele intr-un graf orientat.

void CitireActivitati(vector<string>& activitati, GrafMatrice& graf)

// Citire dependinte

while (true)

else

cout << 'Activitate inexistenta!' << endl;

}

void main()

7 Conexitate

Proprietatile de conexitate ale grafurilor au o mare importanta in rezolvarea problemelor practice. Cele mai importante notiuni referitoare la acest domeniu sunt:

Lant Se numeste lant o lista de noduri de forma cu proprietatea ca . Daca lantul respecta si proprietatea , atunci lantul este bidirectional.

Ciclu Se numeste ciclu o lista de noduri de forma cu proprietatea ca si . Un graf care nu contine cicluri se numeste graf aciclic.

Conex: Un graf se numeste conex daca intre oricare doua noduri din G exista un lant.

Componente conexe: Un subgraf G` se numeste componenta conexa a unui graf G daca este conex si nu exista nici un lant intre un nod din G` si nod din G neinclus in G`.

Tare conex: Un graf se numeste tare conex daca intre oricare doua noduri din G exista un lant bidirectional.

Componente tare conexe: Un subgraf G` se numeste componenta tare conexa a unui graf G daca este tare conex maximal si nu exista nici un lant bidirectional intre un nod din G` si nod din G neinclus in G`.

Componentele tare conexe se pot determina folosind parcurgerea in adancime si sortarea topologica. Algoritmul are trei etape:

Se sorteaza topologic graful G

Se calculeaza graful transpus G` (contine muchiile inversate)

Se parcurge in adancime graful G considerand nodurile in ordinea indicata de sortarea topologica

Arborii astfel obtinuti constituie componentele tare conexe ale grafului. Codul C++ pentru implementarea algoritmului este:

void ComponenteConexe(Graf& g, vector<int>& predecesori)

// 3. Parcurgem in adancime graful transpus considerand

// nodurile in ordinea indicata de sortarea topologica

int nrNoduri = g.NumarNoduri();

vector<CuloriGraf> culori(nrNoduri, Alb);

predecesori = vector<int>(nrNoduri, Graf::NOD_INEXISTENT);

tInceput = vector<int>(nrNoduri,0);

tSfarsit = vector<int>(nrNoduri,0);

int timp = 0;

// pentru fiecare nod din graf

for(int i = 0; i < nrNoduri; i++)

// daca nu a fost inca vizitat

if (culori[noduri[i]] == Alb)

// exploram subgraful corespunzator

ExplorareNod(gt, timp, i, tInceput, tSfarsit, predecesori, culori);

Problema 5

O companie aeriana efectueaza curse intre mai multe orase. Cunoscandu-se legaturile existente intre orase, sa se determine grupele de orase legate prin curse aeriene (intre doua orase din aceeasi grupa trebuie sa existe posibilitatea de a calatori direct sau indirect in ambele sensuri).

Rezolvare

Problema poate fi modelata folosind un graf orientat in care orasele sunt reprezentate prin noduri iar legaturile prin muchii. Citirea datelor se va face dupa modelul prezentat in problema 4.

Grupele de orase sunt echivalente cu componentele tare conexe ale grafului. Acestea vor fi determinate pe baza algoritmului prezentat. Afisarea grupelor se face prin parcurgerea recursiva a arborilor obtinuti.

#include <iostream>

#include <vector>

#include <string>

#include <algorithm>

using namespace std;

#include 'Graf.h'

#include 'GrafMatrice.h'

#include 'GrafAlgoritmi.h'

// Functia pentru citirea datelor de intrare

void CitireDate(vector<string>& orase, GrafMatrice& graf)

// Citire dependinte

while (true)

else

cout << 'Oras inexistenta!' << endl;

}

void AfisareGrupa(vector<string>& orase, vector<int>& predecesori, int codOras)

void main()

8 Drumuri minime in grafuri

In multe probleme din domeniul economic este necesara calcularea drumurilor de cost minim de la un nod sursa la celelalte noduri ale grafului. Unul dintre algoritmi folositi pentru aceasta este algoritmul lui Dijkstra.

Algoritmul lui Dijkstra este un algoritm de tip greedy care porneste de la un graf conex orientat aciclic si de la un nod sursa si determina drumurile si distantele minime pana la toate celelalte noduri. Initial toate nodurile sunt considerate neprocesate. La fiecare pas se selecteaza nodul neprocesat cu distanta minima pana la nodul sursa si se imbunatatesc drumurile existente folosind acest nod.  Algoritmul se incheie atunci cand toate nodurile au fost procesate.

Codul C++ pentru implementarea algoritmului este

void DrumuriMinime(Graf& g, int sursa, vector<int>& distante, vector<int>& predecesori)

// obtinem lista de noduri adiacente

list<int> noduri = g.NoduriAdiacente(nodCurent);

// parcurgem lista

list<int>::iterator iter = noduri.begin();

for (int i = 0; i < (int)noduri.size(); i++, iter++)

if (distante[(*iter)] >

distante[nodCurent] + g.ValoareMuchie(nodCurent,(*iter)))

// Marcam nodul ca procesat

culori[nodCurent] = Negru;

nrNoduriProcesate++;

}

Problema 6

O societate comerciala detine intr-un oras 3 centre de aprovizionare cu produse lactate si n de centre de desfacere. Se cunosc drumurile posibile intre centre si distantele asociate acestora.

Se cere sa se determine pentru fiecare centru de desfacere depozitul de la care sa se faca aprovizionarea si ruta corespunzatoare astfel incat distanta parcursa sa fie minima.

Rezolvare

Se construieste un graf neorientat in care centrele sunt reprezentate prin noduri numerotate 0, 1, 2, 3, ., n+2 (centrele de aprovizionare sunt numerotate cu 0,1,2) si drumurile posibile impreuna cu distantele aferente prin muchii. Se presupune ca datele asociate grafului sunt stocate intr-un fisier sub forma de liste de adiacenta.

Pentru rezolvarea problemei vom aplica algoritmul lui Dijkstra pentru a determina drumurile minime de le cele trei depozite la centrele de desfacere. Pentru fiecare centru se va determina depozitul cel mai apropiat si se va reconstitui drumul catre acesta.

#include <iostream>

#include <fstream>

using namespace std;

#include 'Graf.h'

#include 'GrafMatrice.h'

#include 'GrafAlgoritmi.h'

// numele fisierului care contine graful

const char* const numeFisier = 'l_dijkstra.txt';

void AfisareDrum(int nod, vector<int>& predecesori)

cout << endl;

void main()

else if (distante1[i] < distante0[i] && distante1[i] < distante2[i])

else

}