Notiuni de baza privind sistemele

Notiuni de baza privind sistemele

Terminologie

Prin sistem se intelege un ansamblu de obiecte care interactioneaza cu mediul exterior, obiectele fiind interconectate sau reciproc independente.

Interactiunea cu mediul are loc in ambele sensuri si consta in transfer de energie, masa si/sau informatie.

In general se presupune ca mediul exterior are inertie infinita (mediul nu reactioneaza la prezenta sistemului, spre deosebire de sistem, care reactioneaza la actiunea mediului exterior).

In figura 1, obiectele care compun sistemul S, si anume S1, S2, S3, S4 pot fi interconectate, ca de exemplu S2, S3 si S4 sau independente, ca si S1. Daca sistemul S contine numai obiecte interconectate, atunci se numeste sistem primar sau propriu-zis. Obiectele pot fi de diverse naturi, chiar abstracte. Cand obiectele sunt concrete se vorbeste despre un sistem fizic.

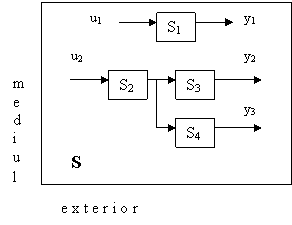
Figura 1

Studiul sistemelor fizice este greu de realizat in mod nemijlocit. De aceea, de regula, studiul se face pe modele ale sistemelor fizice, cel mai des pe modele abstracte. Cele mai raspandite modele abstracte sunt modelele matematice.

Datorita faptului ca obiectele care compun un sistem pot fi de orice natura, teoria sistemelor este extrem de generala, ea acopera aplicatii din numeroase domenii: tehnic, medical, economic etc.

Prin marimile u₁ si u₂ mediul actioneaza asupra sistemului S. Acestea se numesc marimi de intrare.

Sistemul actioneaza asupra mediului prin marimile y₁, y₂ si y₃, care poarta numele de marimi de iesire. Actiunea acestora este doar de tip comunicare.

In mod obisnuit, marimile care caracterizeaza un sistem se reprezinta sub forma vectoriala astfel:

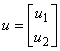si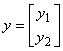

Observatie: In general se lucreaza numai cu vectori coloana. Astfel, un vector linie se scrie ca transpusa unui vector coloana.

Numarul marimilor de intrare se noteaza cu m, iar al celor de iesire cu p. Dimensiunile celor doi vectori, de intrare u si de iesire y sunt u(m x 1), respectiv y(p x 1).

Operatia de precizare a intrarilor si iesirilor unui sistem poarta numele de orientare a sistemului. Spunem ca sistemul este orientat de la u la y (u y). Orientarea este legata de interpretarea cauzala a unui sistem, in sensul ca marimile de intrare sunt considerate marimi cauza, iar cele de iesire marimi efect, iar efectul nu poate sa preceada cauza.

Interpretarea cauzala este la randul ei legata de cea dinamica, in sensul ca interactiunile sistemului cu mediul exterior au loc in timp. Timpul este singura variabila independenta a problemei, deci atat marimile de intrare, cat si cele de iesire sunt functii de timp, iar sistemul poate fi privit ca un ansamblu care prelucreaza functiile de intrare furnizand pe cele corespunzatoare marimilor de iesire. In acest context vorbim despre sistem dinamic.

Obiectele care compun un sistem se mai numesc si subsisteme. In exemplul dat apar patru susbsisteme: S₁, S₂, S₃, S₄. Fiecare dintre ele are la randul lui intrari si iesiri, deci este posibila o ierarhizare cu un numar oricat de mare de niveluri. Din acest motiv vorbim de regula numai despre sisteme, intelegand din context care este nivelul ierarhic al sistemului respectiv.

Convenim sa reprezentam un sistem printr-un bloc si sageti, unde sagetile corespund marimilor de intrare si de iesire, iar blocul in care se noteaza numele sistemului sau informatii

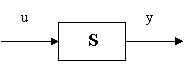
Se disting trei tipuri fundamentale de conexiuni ale sistemelor:

a)      conexiunea serie,

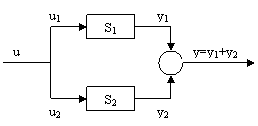
b)      conexiunea derivatie (paralel) si

c)      conexiunea cu reactie.

In urma interconectarii a doua sisteme rezulta un nou sistem. Comportarea acestuia este determinata de proprietatile de interconectare ale sistemelor componente. Spunem ca in cadrul unui sistem sistemele componente sunt separabile daca in urma cuplarii fiecare subsistem al conexiunii se comporta dupa aceleasi reguli ca si inainte de cuplare, adica la fel ca si in cazul in care ar fi independent.   Numai in acest context este valabila reprezentarea prin scheme bloc de tipul celor prezentate in figura 2:

a)      conexiunea serie  b) conexiunea paralel

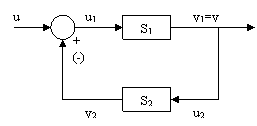
c) conexiunea cu reactie

Figura 2

Observatii: 1) In cazul conexiunii cu reactie, daca reactia este pozitiva (la sumator se considera semnul +) u₁=u+y₂ , iar daca reactia este negativa u₁=u-y₂.

2) Sirul u, u₁, S₁, y se numeste cale directa, iar sirul y, S₂, y₂ se numeste cale de reactie (feed-back).

3) Reactia negativa are rol stabilizator, iar sistemul cu reactie pozitiva este instabil.

4) Din punct de vedere tehnic, conexiunea a doua sisteme respecta principiul cauzalitatii daca consumul de la elementul din aval luat de elementul din amonte este neglijabil.

Prin semnal se intelege o marime fizica masurabila provenita de la un generator (sistemul amonte) si destinata unui receptor (sistemul aval).

Marimea numita semnal se considera insotita de una sau mai multe caracteristici purtatoare de informatii relativ la una sau mai multe marimi asociate.

Interactiunea sistemului cu mediul exterior sau a sistemelor fizice intre ele se realizeaza prin semnale. Astfel, este evident faptul ca teoria sistemelor se bazeaza pe teoria semnalelor.

Cele mai frecvente variabile informationale (marimi asociate unui semnal) sunt: amplitudinea, puterea, durata semnalului (atunci cand este modulat in durata), energia asociata unui interval de timp bine precizat.

De regula, semnalele respectiv marimile purtatoare de informatii sunt caracterizate prin modele matematice care sunt aplicatii de forma:

c : T M  (1)

unde M este multimea de valori asociata variabilei informationale iar T este multimea timp.

Acesteia din urma i se asociaza fie o multime continua care este o submultime a multimii numerelor reale T=R⁺=[0, +¥), fie o multime discreta de momente echidistante T=. In primul caz se vorbeste despre sisteme in timp continuu (STC), iar in al doilea caz de sisteme in timp discret (STD).

In cazul sistemelor in timp discret se pot utiliza si unele notatii simplificate, cum ar fi:

T== sau T==

In consecinta, exprimari de forma u(k^.h), u(k), u(t) se considera in cazul STD echivalente. Ultimele doua exprimari presupun inteleasa conventia ca argumentul are o valoare relativa si anume reprezinta numarul de intervale de timp de lungime h (interval catre poarta numele de pas de discretizare a timpului, perioada de discretizare sau perioada de esantionare).

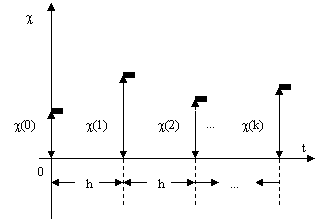
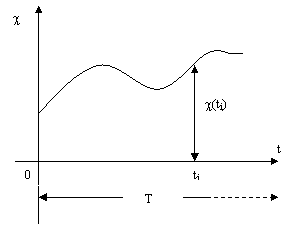
a) cazul STC b) cazul STD

Figura 3

Observatie: Ca urmare a renuntarii la notarea argumentelor sub forma k^.h sau k^.t, notatiile utilizate trebuie interpretate cu atentie, bunaoara notatia y(2) inseamna pentru un STC valoarea lui y la momentul t=2sec, iar pentru un STD valoarea lui y la momentul t=2^.h. Astfel, daca h=0.1sec y(2) semnifica valoarea lui y la momentul t=0.2sec, iar daca h=10sec, valoarea lui y la momentul t=20sec.

Prin semnal analogic se intelege un semnal definit in timp continuu, avand variatii continue si al carui domeniu M al valorilor variabilelor informationale este un ansamblu continuu. Dispozitivele, aparatele si echipamentele care lucreaza cu semnale analogice se numesc analogice.

Prin semnal numeric se intelege un semnal in timp discret si cuantificat, a carui variabila informationala este reprezentata de o secventa de numere. In mod obisnuit, semnalele numerice sunt asociate semnalelor esantionate si cuantizate, unitatea numerica corespunzand unei cuante. Dispozitivele, aparatele si echipamentele care lucreaza cu semnale numerice se numesc numerice sau digitale.

In teoria sistemelor, in locul sistemelor fizice se lucreaza cu modele abstracte ale acestora. Cele mai utilizate dintre acestea sunt modelele matematice. In mod frecvent de folosesc doua categorii de modele matematice:

- modele matematice functionale sau modele matematice intrare-iesire (MM-II) si

modele matematice structural-functionale sau modele matematice intrare-stare-iesire (MM-ISI).

MM-II opereaza numai cu modelele asociate semnalelor de intrare si de iesire, adica cu modelele semnalelor prin care se descrie, in relatia cu exteriorul, comportarea sau functionarea sistemului.

MM-ISI utilizeaza inca o categorie de marimi, numite marimi de stare notate cu x, care se asociaza interiorului sistemului, adica structurii sistemului. Numarul acestora se noteaza cu n.

Marimile de stare sunt prin definitie acele marimi care pe de o parte permit determinarea in orice moment a oricarei marimi de iesire cu ajutorul marimilor de intrare, iar pe de alta parte permit determinarea in orice moment a tendintei de variatie a sistemului. Celor doua aspecte le corespund doua tipuri de ecuatii:

- ecuatii de iesire de forma: y(t)=g(x(t), u(t)) (2)

- ecuatii de stare de forma:=f(x(t), u(t)) pentru STC (3)

x(t+1)= f(x(t), u(t)) (4)

Functia f este o functie vectoriala alcatuita din n functii scalare de variabile vectoriale, iar g este o functie vectoriala alcatuita din p functii scalare de variabile vectoriale.

Variabilele de stare, prin modul in care sunt definite, descriu procese elementare de cumulare de energie, masa sau informatie. Ele descriu modificarea unui continut de la un moment la altul. Din aceasta observatie provine un criteriu practic de alegere a variabilelor de stare. De eexemplu, se pot alege ca variabile de stare urmatoarele marimi: tensiunea la bornele unui condensator, curentul printr-o inductanta, temperatura unui obiect, pozitia sau viteza unui obiect.

Relatia dintre un sistem fizic si unul abstract se poate caracteriza prin notiunile la care se refera figura 4:

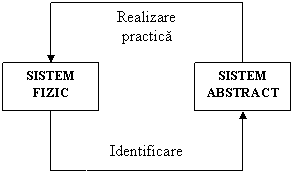
Figura 4

Prin identificare se intelege operatia prin care unui sistem fizic i se asociaza un sistem abstract. Identificabilitatea este proprietatea unui sistem de a permite aceasta operatie.

Realizarea fizica este operatia prin care unui sistem abstract i se asociaza un sistem fizic, iar realizabilitatea este proprietatea unui sistem de a permite aceasta operatie.

Cele doua operatii sunt importante in urmatorul context: pentru a putea studia un sistem fizic in mod complet, este necesar ca acesta sa fie identificat, deoarece pe un model se pot studia inclusiv strategii distructive. Pe de alta parte, pentru un sistem fizic se pune problema influentarii acestuia de catre om in mod direct sau indirect in sistemele automate. Sistemele de conducere actioneaza dupa diferite algoritme, care se sintetizeaza pe baza modelului sistemului fizic. Realizabilitatea garanteaza in schimb transpunerea unui algoritm intr-un dispozitiv fizic de comanda. In acest context, intereseaza intotdeauna daca modelele cu care lucram sunt sau nu realizabile.

STRUCTURI DE SISTEME DE CONDUCERE

Un proces tehnic (o instalatie tehnica) si prin extensie un proces fizic necesita aducerea intr-un anumit regim de functionare. In linii mari este vorba de despre o problema de conducere, procesul trebuie condus dintr-un regim initial intr-un regim de functionare dorit.

Procesului trebuie sa i se poata modifica regimul de functionare. Operatia de asigurare a regimului de functionare trebuie sa se realizeze si atunci cand procesul este perturbat de factori externi.

Intrarile au fost impartite in doua categorii: - u sunt marimile de intrare aflate sub controlul operatorului (marimi de comanda) si - v sunt marimile de intrare care nu depind de operator; ele redau influenta mediului exterior (marimi perturbatoare) y este marimea de iesire.

Probleme de acest gen se abordeaza asociind procesului, in principiu, schema bloc din figura 5:

Figura 5

Un anumit regim de functionare se exprima in cazul general printr-o anumita functie asociata iesirii y^*(t).

Problema de conducere este problema determinarii unei functii de comanda u(t) astfel incat la iesire sa obtinem y(t)= y^*(t). Acest deziderat este, de la caz la caz, afectat intr-o masura neesentiala sau foarte importanta de existenta marimilor perturbatoare, adica a unor variatii v(t).

Din aceasta observatie deriva cele doua structuri fundamentale de conducere, si anume:

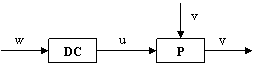
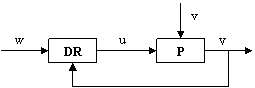
a) SCCD b) SCCI

Figura 6

a)      Structura de conducere in circuit deschis (SCCD), a carei schema bloc de principiu este prezentata in figura 6a) se caracterizeaza prin faptul ca procesul se gaseste sub actiunea dispozitivului de comanda DC.

Functia y^*(t) este prescrisa prin marimea de conducere w, respectiv prin functia w(t).

Din aceasta, DC sintetizeaza functia de comanda u(t) astfel incat la iesire sa se obtina y(t)= y^*(t). Astfel, se poate scrie:

y(t)=F , respectiv  u(t)=F^-1

Principiul de conducere in circuit deschis se foloseste in urmatoarele cazuri:

- procesul P este stabil si perturbatiile sunt neglijabile;

- procesul P este stabil, forma perturbatiilor este bine precizata si "a priori" cunoscuta si reproductibila.

O buna parte din automatizari se bazeaza pe aceasta structura, in acest caz utilizandu-se cu predilectie ca dispozitiv de comanda automatele programabile.

b)      Structura de conducere in circuit inchis (SCCI) prezentata in figura 6b) este o structura cu reactie.

Functia de comanda u(t) este elaborata in permanenta de dispozitivul de reglare DR, in timp continuu sau discret (cu un pas de esantionare h redus).

u(t)=A , unde A este algoritmul de reglare de reglare.

Prin w(t) se prescrie y^*(t). Algoritmul este astfel conceput incat prin functia de comanda u(t) sa se sigure conditia y(t) y (t) oricare ar fi functiile perturbatoare v(t).

Aceasta structura se utilizeaza in situatiile in care:

- procesul este instabil si/sau

- efectul perturbatiilor este puternic.

In mod obisnuit operatiile de comanda si reglare se fac automat. DC si DR sunt denumite dispozitive de automatizare.

Observatie: In limba engleza nu se face distinctie intre comanda si reglare, acest lucru rezultand din context. In comun pentru cele doua actiunui (conducere si reglare) se foloseste denumirea de control.

Ansamblul celor doua structuri de conducere (SCCD si SCCI) reprezinta ansamblul sistemelor de conducere a proceselor. In acest context se pune problema ca dispozitivele de conducere sa actioneze in mod automat (fara prezenta operatorului uman). O astfel de cerinta decurge din diverse motive.

Exista situatii cand este foarte dificila efectuarea operatiilor de catre om, intrucat fie omul nu are acces la comanda, fie trebuie sa actioneze foarte rapid. O alta categorie de situatii se refera la cazurile in care trebuie marit randamentul operatiunilor de comanda. In alte situatii, energia necesara pentru comanda efectiva trebuie sa fie foarte mare si aceasta conditie nu poate fi indeplinita decat printr-un sistem automat.