Notiuni de teoria sistemelor

Preliminarii

1.1. Conceptul de sistem. Terminologii asociate

Prin sistem se intelege un ansamblu de obiecte care interactioneaza cu mediul exterior, obiectele fiind interconectate sau reciproc independente.

Interactiunea cu mediul are loc in ambele sensuri si consta in transfer de energie, masa si/sau informatie. In general se presupune ca mediul exterior are inertie infinita (mediul nu reactioneaza la prezenta sistemului, spre deosebire de sistem, care reactioneaza la actiunea mediului exterior).

In figura 1, obiectele care compun sistemul S, si anume S1, S2, S3, S4 pot fi interconectate, ca de exemplu S2, S3 si S4 sau independente, ca si S1. Daca sistemul S contine numai obiecte interconectate, atunci se numeste sistem primar sau propriu-zis. Obiectele pot fi de diverse naturi, chiar abstracte. Cand obiectele sunt concrete se vorbeste despre un sistem fizic. Studiul sistemelor fizice este greu de realizat in mod nemijlocit. De aceea, de regula, studiul se face pe modele ale

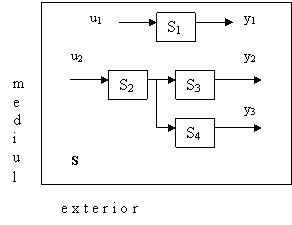
Figura 1

sistemelor fizice, cel mai des pe modele abstracte. Cele mai raspandite modele abstracte sunt modelele matematice.

Datorita faptului ca obiectele care compun un sistem pot fi de orice natura, teoria sistemelor este extrem de generala, ea acopera aplicatii din numeroase domenii: tehnic, medical, economic etc.

Prin marimile u₁ si u₂ mediul actioneaza asupra sistemului S. Acestea se numesc marimi de intrare.

Sistemul actioneaza asupra mediului prin marimile y₁, y₂ si y₃, care poarta numele de marimi de iesire. Actiunea acestora este doar de tip comunicare.

In mod obisnuit, marimile care caracterizeaza un sistem se reprezinta sub forma vectoriala astfel:

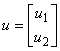si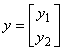

Observatie: In general se lucreaza numai cu vectori coloana. Astfel, un vector linie se scrie ca transpusa unui vector coloana.

Numarul marimilor de intrare se noteaza cu m, iar al celor de iesire cu p. Dimensiunile celor doi vectori, de intrare u si de iesire y sunt u(m x 1), respectiv y(p x 1).

Operatia de precizare a intrarilor si iesirilor unui sistem poarta numele de orientare a sistemului. Spunem ca sistemul este orientat de la u la y (u y). Orientarea este legata de interpretarea cauzala a unui sistem, in sensul ca marimile de intrare sunt considerate marimi cauza, iar cele de iesire marimi efect, iar efectul nu poate sa preceada cauza.

Interpretarea cauzala este la randul ei legata de cea dinamica, in sensul ca interactiunile sistemului cu mediul exterior au loc in timp. Timpul este singura variabila independenta a problemei, deci atat marimile de intrare, cat si cele de iesire sunt functii de timp, iar sistemul poate fi privit ca un ansamblu care prelucreaza functiile de intrare furnizand pe cele corespunzatoare marimilor de iesire. In acest context vorbim despre sistem dinamic.

Obiectele care compun un sistem se mai numesc si subsisteme. In exemplul dat apar patru susbsisteme: S₁, S₂, S₃, S₄. Fiecare dintre ele are la randul lui intrari si iesiri, deci este posibila o ierarhizare cu un numar oricat de mare de niveluri. Din acest motiv vorbim de regula numai despre sisteme, intelegand din context care este nivelul ierarhic al sistemului respectiv.

Convenim sa reprezentam un sistem printr-un bloc si sageti, unde sagetile corespund marimilor de intrare si de iesire, iar blocul in care se noteaza numele sistemului sau informatii

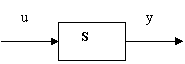
Se disting trei tipuri fundamentale de conexiuni ale sistemelor:

a)      conexiunea serie,

b)      conexiunea derivatie (paralel) si

c)      conexiunea cu reactie.

In urma interconectarii a doua sisteme rezulta un nou sistem. Comportarea acestuia este determinata de proprietatile de interconectare ale sistemelor componente. Spunem ca in cadrul unui sistem sistemele componente sunt separabile daca in urma cuplarii fiecare subsistem al conexiunii se comporta dupa aceleasi reguli ca si inainte de cuplare, adica la fel ca si in cazul in care ar fi independent. Numai in acest context este valabila reprezentarea prin scheme bloc de tipul celor prezentate in figura 2:

a)      conexiunea serie b) conexiunea paralel

c) conexiunea cu reactie

Figura 2

Observatii: 1) In cazul conexiunii cu reactie, daca reactia este pozitiva (la sumator se considera semnul +) u₁=u+y₂ , iar daca reactia este negativa u₁=u-y

2) Sirul u, u₁, S₁, y se numeste cale directa, iar sirul y, S₂, y₂ se numeste cale de reactie (feed-back).

3) Reactia negativa are rol stabilizator, iar sistemul cu reactie pozitiva este instabil.

4) Din punct de vedere tehnic, conexiunea a doua sisteme respecta principiul cauzalitatii daca consumul de la elementul din aval luat de elementul din amonte este neglijabil.

Prin semnal se intelege o marime fizica masurabila provenita de la un generator (sistemul amonte) si destinata unui receptor (sistemul aval). Marimea numita semnal se considera insotita de una sau mai multe caracteristici purtatoare de informatii relativ la una sau mai multe marimi asociate. Interactiunea sistemului cu mediul exterior sau a sistemelor fizice intre ele se realizeaza prin semnale. Astfel, este evident faptul ca teoria sistemelor se bazeaza pe teoria semnalelor.

Cele mai frecvente variabile informationale (marimi asociate unui semnal) sunt: amplitudinea, puterea, durata semnalului (atunci cand este modulat in durata), energia asociata unui interval de timp bine precizat. De regula, semnalele respectiv marimile purtatoare de informatii sunt caracterizate prin modele matematice care sunt aplicatii de forma:

c : T M  (1)

unde M este multimea de valori asociata variabilei informationale iar T este multimea timp. Acesteia din urma i se asociaza fie o multime continua care este o submultime a multimii numerelor reale T=R⁺=[0, +¥), fie o multime discreta de momente echidistante T=. In primul caz se vorbeste despre sisteme in timp continuu (STC), iar in al doilea caz de sisteme in timp discret (STD).

In cazul sistemelor in timp discret se pot utiliza si unele notatii simplificate, cum ar fi:

T== sau T==

In consecinta, exprimari de forma u(k^.h), u(k), u(t) se considera in cazul STD echivalente. Ultimele doua exprimari presupun inteleasa conventia ca argumentul are o valoare relativa si anume reprezinta numarul de intervale de timp de lungime h (interval catre poarta numele de pas de discretizare a timpului, perioada de discretizare sau perioada de esantionare).

a) cazul STC b) cazul STD

Figura 3

Observatie: Ca urmare a renuntarii la notarea argumentelor sub forma k^.h sau k^.t, notatiile utilizate trebuie interpretate cu atentie, bunaoara notatia x(2) inseamna pentru un STC valoarea lui x la momentul t=2sec, iar pentru un STD valoarea lui x la momentul t=h. Astfel, daca h=0.1sec x(2) semnifica valoarea lui x la momentul t=0.2sec, iar daca h=10sec, valoarea lui x la momentul t=20sec.

Prin semnal analogic se intelege un semnal definit in timp continuu, avand variatii continue si al carui domeniu M al valorilor variabilelor informationale este un ansamblu continuu. Dispozitivele, aparatele si echipamentele care lucreaza cu semnale analogice se numesc analogice.

Prin semnal numeric se intelege un semnal in timp discret si cuantificat, a carui variabila informationala este reprezentata de o secventa de numere. In mod obisnuit, semnalele numerice sunt asociate semnalelor esantionate si cuantizate, unitatea numerica corespunzand unei cuante. Dispozitivele, aparatele si echipamentele care lucreaza cu semnale numerice se numesc numerice sau digitale.

In teoria sistemelor, in locul sistemelor fizice se lucreaza cu modele abstracte ale acestora. Cele mai utilizate dintre acestea sunt modelele matematice. In mod frecvent de folosesc doua categorii de modele matematice:

- modele matematice functionale sau modele matematice intrare-iesire (MM-II) si

modele matematice structural-functionale sau modele matematice intrare-stare-iesire (MM-ISI).

MM-II opereaza numai cu modelele asociate semnalelor de intrare si de iesire, adica cu modelele semnalelor prin care se descrie, in relatia cu exteriorul, comportarea sau functionarea sistemului.

MM-ISI utilizeaza inca o categorie de marimi, numite marimi de stare notate cu x, care se asociaza interiorului sistemului, adica structurii sistemului. Numarul acestora se noteaza cu n. Marimile de stare sunt prin definitie acele marimi care pe de o parte permit determinarea in orice moment a oricarei marimi de iesire cu ajutorul marimilor de intrare, iar pe de alta parte permit determinarea in orice moment a tendintei de variatie a sistemului. Celor doua aspecte le corespund doua tipuri de ecuatii:

- ecuatii de iesire de forma: y(t)=g(x(t), u(t)) (2)

- ecuatii de stare de forma:=f(x(t), u(t)) pentru STC (3)

x(t+1)= f(x(t), u(t)) (4)

Functia f este o functie vectoriala alcatuita din n functii scalare de variabile vectoriale, iar g este o functie vectoriala alcatuita din p functii scalare de variabile vectoriale.

Variabilele de stare, prin modul in care sunt definite, descriu procese elementare de cumulare de energie, masa sau informatie. Ele descriu modificarea unui continut de la un moment la altul. Din aceasta observatie provine un criteriu practic de alegere a variabilelor de stare. De eexemplu, se pot alege ca variabile de stare urmatoarele marimi: tensiunea la bornele unui condensator, curentul printr-o inductanta, temperatura unui obiect, pozitia sau viteza unui obiect etc.

Relatia dintre un sistem fizic si unul abstract se poate caracteriza prin notiunile la care se refera figura 4:

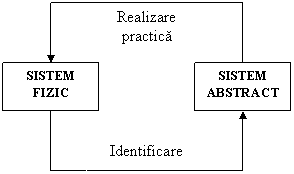
Figura 4

Prin identificare se intelege operatia prin care unui sistem fizic i se asociaza un sistem abstract. Identificabilitatea este proprietatea unui sistem de a permite aceasta operatie.

Realizarea fizica este operatia prin care unui sistem abstract i se asociaza un sistem fizic, iar realizabilitatea este proprietatea unui sistem de a permite aceasta operatie.

Cele doua operatii sunt importante in urmatorul context: pentru a putea studia un sistem fizic in mod complet, este necesar ca acesta sa fie identificat, deoarece pe un model se pot studia inclusiv strategii distructive. Pe de alta parte, pentru un sistem fizic se pune problema influentarii acestuia de catre om in mod direct sau indirect in sistemele automate. Sistemele de conducere actioneaza dupa diferite algoritme, care se sintetizeaza pe baza modelului sistemului fizic. Realizabilitatea garanteaza in schimb transpunerea unui algoritm intr-un dispozitiv fizic de comanda. In acest context, intereseaza intotdeauna daca modelele cu care lucram sunt sau nu realizabile.

1. Conceptul de sistem liniar

Se considera un sistem S orientat de la u la y si asupra lui se efectueaza trei experimente.

E1 Se aplica la intrare u(t)=u₁(t) in conditii initiale CI₁. Presupunem ca la iesire se obtine y(t)=y₁(t).

E2 Se aplica la intrare u(t)=u₂(t) in conditii initiale CI Presupunem ca la iesire se obtine y(t)=y₂(t).

E3 Se aplica la intrare u(t)=c₁^. u₁(t)+ c u₂(t) in conditii initiale c₁^.CI₁+ cCI Presupunem ca la iesire se obtine y(t)=y₃(t).

Spunem ca sistemul S este liniar daca oricare ar fi u₁(t), u₂(t), CI₁, CI₂, c₁ si c₂, in al treilea experiment va rezulta ca y(t)=c₁^. y₁(t)+ c y₂(t).

Contraexemplu: y=ax+b.

Criteriul de recunoastere practica a unui model matematic liniar este urmatorul: toti termenii din expresia modelului trebuie sa fie de gradul I in raport cu variabilele care apar in model. Daca apar termeni de grad 0 sau mai mare sau egal cu II, modelul este neliniar.

Cazul sistemelor liniare este deosebit de important din punct de vedere stiintific, intrucat pentru astfel de sisteme au fost eleborate metode de analiza si sinteza extrem de bine puse la punct. Din acest motiv se prefera ca sistemelor fizice sa li se asocieze modele matematice liniare. In realitate, aproape toate sistemele fizice sunt neliniare.

Din acest punct de vedere se vorbeste despre doua categorii de neliniaritati:

neliniaritati esentiale, care nu se pot inlocui printr-un MM liniar de aproximare;

neliniaritati neesentiale, care se pot inlocui prin MM liniare de aproximare.

Cu unele exceptii, orice marime fizica ia valori intr-un domeniu limitat. In cazul liniar se presupune ca fiecare marime care apare in modelele sistemelor liniare poate lua orice valoare reala. Intrucat fiecare din aceste marimi ia valori doar in subintervale din multimea numerelor reale rezulta ca modelele nu sunt general valabile, ele sunt valabile doar pe aceste intervale, in consecinta nu mai poate fi aplicata conditia "oricare ar fi c₁ si c₂"din definitia unui sistem liniar.

Observatie: Atributul de "liniar" inglobeaza proprietatile de superpozitie si omogenitate. Acest lucru trebuie inteles astfel: daca in definitia liniaritatii c₁= c₂=1 se obtine principiul superpozitiei, iar daca c₁= c si c₂=0 sau c₂= c si c₁=0 rezulta o amplificare denumita in matematica omogenitate.

Elemente de transfer neliniare

Se numeste element de transfer un sistem cu o singura marime de intrare si o singura marime de iesire pentru care intereseaza modul in care din u(t) rezulta y(t), privit ca transfer al informatiei de la intrare la iesire.

Sistemele cu o singura marime de intrare si o singura marime de iesire se regasesc in literatura de specialitate sub prescurtarea SISO (Single Input-Single Output), iar cele cu mai multe marimi de intrare si/sau de iesire sub prescurtarea MIMO (Multi Input-Multi Output).

Un sistem neliniar este un sistem pentru care nu este valabila definitia data in paragraful anterior. De regula, un sistem rezulta prin interconectarea mai multor subsisteme sau a mai multor elemente de tranfer. Este sufucient ca unul singur dintre acestea sa fie neliniar pentru ca ansamblul sa fie neliniar.

In cazul neliniaritatilor esentiale se cauta ca modelele neliniare sa fie inlocuite cu modele liniare prin operatia de liniarizare. Neliniaritatile esentiale nu se inlocuiesc cu modele liniare deoarece sunt foarte importante prin faptul ca uneori caracterizeaza diverse interactiuni fizice, iar alteori caracterizeaza anumite maniere de prelucrare a informatiei.

In anexa 1 se prezinta o serie de elemente de transfer neliniare intalnite mai des in practica.

In afara elementelor prezentate in anexa 1, se intalnesc numeroase alte neliniaritati, dar acestea apar cel mai des. Ele sunt asociate fie procesului condus, fie dispozitivului de automatizare. In cel de-al doilea caz se urmaresc diferite efecte, de exemplu: se utilizeaza regulatoare bipozitionale si tripozitionale in varianta analogica sau numerica deoarece au avantajul de a fi simple constructiv in primul caz si, respectiv algoritmic in al doilea caz.

Intereventia regulatorului asupra procesului condus se face prin intermediul elementelor de executie. Ele adapteaza pe de o parte marimea de comanda la necesitatile impuse de proces (din punct de vedere al naturii si domeniului de variatie), iar pe de alta parte faciliteaza transmiterea de cantitati importante de energie spre proces. Astfel de echipamente sunt in general costisitoare si in mod obisnuit au o parte predominant mecanica. Problemele cele mai frecvente legate de elementele de executie sunt cele legate de intretinere si uzura, datorita faptului ca in componenta lor apar elemente in miscare. Pentru a proteja cat de cat elementele de excutie este necesar sa facem astfel incat acesta sa nu reactioneze la perturbatii, oricat ar fi de mici. In acest scop se utilizeaza elemente de transfer cu zone de insensibilitate (ET-ZI).

Modele matematice ale sistemelor

O prima clasificare a MM a fost prezentata in paragraful 1.1. Indiferent de tipul lor, MM reprezinta operatori. In ultima instanta, acesti operatori se aplica functiilor de intrare si furnizeaza functii de iesire.

Modele matematice intrare-iesire (MM-II)

Pentru STC, MM-II este de forma:

f(y(t), y⁽¹⁾(t),,y⁽ⁿ⁾(t), u(t), u⁽¹⁾(t),, u^(m)(t), t)=0 (5)

Pentru a putea fi utilizat, modelului matematic trebuie sa i se asocieze conditii initiale (la fel ca in cazul integrarii ecuatiilor diferentiale). Atunci cand timpul apare explicit se vorbeste despre sisteme variante in timp. Daca timpul nu apare explicit, spunem ca sistemul este invariant in timp. Conditia ca modelul (6) sa fie strict cauzal, fizic realizabil, este ca n>m. Daca n=m sistemul este la limita de cauzalitate, iar daca n<m sistemul este necauzal.

Exemplul 1. Presupunem ca f(y(t), y⁽¹⁾(t),,y⁽ⁿ⁾(t), u(t), u⁽¹⁾(t),, u^(m)(t), t)==0.

Rezulta ca , deci avem de a face cu un sistem pur derivator cu n=0 si m=1, ceea ce indica un sistem necauzal. Motivul este acela ca un sistem fizic nu poate executa operatia de derivare, deoarece ar insemna ca iesirea sa anticipeze variatia intrarii. Modelul pur derivator este totusi utilizat ca model de aproximare a unor modele reale mai complicate care au ca destinatie principala modelarea operatiei de derivare. Astfel, se poate modela operatia de derivare prin urmatoarele modele:

sau

Aceste doua modele efectueaza si operatia de derivare, iar daca a si a sunt foarte mici se poate lucra cu modelul de aproximare .

In situatiile in care f este un operator liniar, ecuatia (6) ia forma (7):

a_ny⁽ⁿ⁾(t)++ a₁y⁽¹⁾(t)+ a₀y(t)= b_mu^(m)(t)++ b₁u⁽¹⁾(t)+ b₀u(t) (6)

a_i cu i=0,, n si b_j cu j=0,, m se numesc coeficienti ai modelului. Acestia pot sa depinda de unul sau mai multi parametri sau pot fi ei insisi parametri.

Atat pentru (6), cat si pentru (7) n (ordinul maxim de derivare al marimii de iesire) poarta numele de ordin al sistemului si este o masura a inertiei care se manifesta in sistem, inertie care se caracterizeaza prin faptul ca variatiile marimii de iesire sunt intarziate in raport cu variatiile marimii de intrare. Cu cat n este mai mare, cu atat procesul de intarziere este mai important. Principial, fiecare unitate a lui n introduce o constanta de timp. Latura anticipativa a sistemului este caracterizata de m (ordinul maxim de derivare a marimii de intrare), intrucat se refera la gradul de aprofundare al tendintei de variatie a marimii de intrare. In consecinta, intr-un sistem dinamic apar atat tendinte de anticipare cat si tendinte de temporizare, ultimele fiind intotdeauna mai puternice daca modelul este strict cauzal.

Pentru STD, forma generala a unui MM-II este urmatoarea:

f(y(t), y(t-1),, y(t-n), u(t), u(t-1),,u(t-m), t)=0 (7)

Daca timpul apare explicit se spune ca sistemul este variant in timp, altfel este invariant in timp. Spre deosebire de (6), care este o ecuatie diferentiala de ordinul n, (8) este o ecuatie recurenta de ordinul n. Ordinul de recurenta este dat de diferenta de ordin intre primul si ultimul termen corespunzatori marimii de iesire: t-(t-n)=n.

Si in acest caz n poarta numele de ordin al sistemului. Daca in ecuatia (8) apar atat y(t) cat si u(t), sistemul este la limita de cauzalitate. Daca in model apare y(t) si nu apare u(t), sistemul este strict cauzal, iar daca apare u(t) si nu apare y(t), sistemul este necauzal. In principiu, modelul (8) trebuie privit ca un operator care permite calculul lui y(t) atunci cand se cunoaste secventa si secventa . Existand y(t) astfel calculat si prin marirea ordinului tuturor argumentelor cu inca o unitate in ecuatia (8), in urmatorul pas de calcul se poate determina recurent y(t+1) s.a.m.d.

In cazul in care operatorul MM-II este liniar, ecuatia (8) ia forma (9):

a_ny(t)++ a₁y(t-1)+ a₀y(t-n)= b_mu(t)++ b₁u(t-1)+ b₀u(t-m) (8)

Pentru a putea utiliza modelele (7) si (8) intr-un caz concret sunt necesare de regula si conditii initiale.

Modele matematice intrare-stare-iesire (MM-ISI)

Pentru STC forma MM-ISI este urmatoarea: 

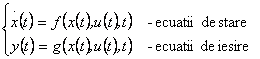(9)

Observatie: Expresiile (9) sunt mai cuprinzatoare decat cele din paragraful 1, unde scopul urmarit era introducerea conceptului de stare.

In ecuatiile (9) x este un vector de forma (n x 1), unde n este acelasi cu cel din expresiile (5) si (6). In acest caz, n indica atat ordinul sistemului, cat si numarul componentelor vectorului de stare x. Din punct de vedere matematic expresiile (5) si (9) pot sa se refere la acelasi sistem, caz in care se poate considera ca (9) rezulta din (5) prin inlocuirea unei ecuatii diferentiale de ordinul n cu n ecuatii diferentiale de ordinul 1 (ecuatiile de stare) sau invers, (5) rezulta din (9) prin eliminarea variabilelor de stare, deci inlocuirea unui system de n ecuatii diferentiale de ordinul 1 cu o singura ecuatie diferentiala de ordinul n.

Pentru STD forma MM-ISI este urmatoarea:

(10)

Si in acest caz este valabila asocierea dintre modelele (7) si (10). Primul reprezinta o relatie de recurenta de ordinul n iar al doilea (prin ecuatiile de stare) reprezinta un sistem de n ecuatii recurente de ordinul 1.

Daca in ecuatiile de iesire din (9) si (10) u(t) apare in mod explicit, atunci sistemul este la limita de cauzalitate, altfel sistemul este strict cauzal. In cazul liniar, (9) si (10) iau formele (9') si (10'):

STC: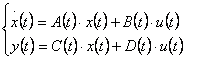 (9')

STD: (10')

In expresiile (9') si (10') A este o matrice patratica de dimensiune (n x n) numita matricea sistemului (sau matricea de evolutie a sistemului) B este o matrice (n x m) si poarta numele de matrice de intrare, C (p x n) reprezinta matricea de iesire, iar D (p x m) este matricea de interconectare intrare-iesire.

Se observa ca (9') si (10') au forme similare si din punct de veder matematic, o intreaga serie de probleme se pun si se rezolva prin aceleasi tehnici de calcul, doar ca se interpreteaza diferit. Aceasta situatie a dus la introducerea variabilelor unificate. Fie v o variabila oarecare. Convenim ca:

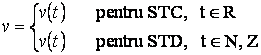
rezultand astfel formele unificate (11) corespunzatoare lui (9) si (10), respectiv (12) corespunzatoare lui (9') si (10'):

(11)

respectiv:

(12)

Matrici si functii de transfer

Definirea matricilor si functiilor de transfer

Conceptul de matrice sau functie de transfer este valabil numai pentru sisteme liniare si este de regula utilizat pentru cazul cand se lucreaza in domeniul operational. Se introduce notiunea de variabila operationala unificata notata cu l, definita astfel:

(13)

In acest caz, unui semnal de intrare u(t) ii corespunde imaginea operationala u(l), iar unui semnal de iesire y(l) ii corespunde imaginea operationala y(l

Pentru un sistem dat S, in conditii initiale nule, y(l) si u(l) sunt legate printr-o relatie de forma:

14)

Functia de legatura H(l) se numeste matrice de transfer, se obtine din modelele matematice ale sistemului si este un invariant. Relatia (14) este valabila numai in conditii initiale nule. Daca conditiile initiale nu sunt nule, in membrul drept mai apar si alti termeni, deductibili din expresia lui H(l). Din moment ce uIR^m si yIR^p, rezulta ca H(l) este o matrice de dimensiuni m x p. Elementul generic al lui H(l) este H_ij(l) si se numeste functie de transfer (f.d.t.).

H(l H_ij l , unde i=1,., p si j=1,., m  (15)

Daca sistemul este de tip SISO, matricea de transfer contine o singura functie de transfer. In acest caz se poate scrie:

(16)

Atat (14), cat si (16) sunt utilizate ca formule de definitie pentru matricea si functia de transfer.

Calculul matricilor si functiilor de transfer pentru STC date prin MM in domeniul timp

Pentru calculul f.d.t. al STC date prin MM-II in domeniul timp se utilizeaza urmatoarele proprietati ale transformatei Laplace:

liniaritatea: 

teorema derivatei:

teorema integrarii: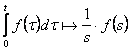

teorema retardarii: .

Se disting mai multe cazuri de calcul, in functie de MM in domeniul timp de la care se porneste si de tipul sistemului:

Sisteme de tip SISO date prin MM-II

Se da sistemul prin MM-II de forma:

a_ny⁽ⁿ⁾(t)++ a₁y⁽¹⁾(t)+ a₀y(t)= b_mu^(m)(t)++ b₁u⁽¹⁾(t)+ b₀u(t) (17)

Pentru calculul functiei de transfer, egalitatea (17) se trece in domeniul operational, in conditii initiale nule si se obtine:

a_n^.s^n.y(s)++ a₁^.s^.y(s)+ a₀^.y(s)= b_m^. s^m.u(s)++ b₁^.s^.u(s)+ b₀^.u(s).

Se aplica apoi definitia (16) si se obtine:

(18)

Se observa ca H(s) apare ca raport al polinoamelor scrise in variabila operationala asociate membrului drept, respectiv stang al MM-II.

Sisteme de tip MIMO date prin MM-ISI

Se da un sistem prin MM-ISI:

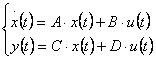(19)

Relatiile (19) se trec in operational si se obtine:

(20)

Din ecuatia de stare din sistemul (13) rezulta:

Þ .

Se inlocuieste acest rezultat in ecuatia de iesire a sistemului (20) si se obtine:

.

Astfel, conform definitiei matricii de transfer se obtine:

(21)

Pentru sisteme de tip SISO, se obtine o functie de transfer de forma:

(22)

Operarea cu matrici si functii de transfer pentru STC are numeroase aplicatii, ca de exemplu calculul rapid si simplu al circuitelor electrice liniare.

Calculul matricilor si functiilor de transfer pentru STD date prin MM in domeniul timp

Calculul matricilor si functiilor de transfer pentru STD date prin MM in domeniul timp se face pe baza urmptoarelor proprietati ale transformatei Z:

liniaritate: 

teorema deplasarii la stanga:

teorema deplasarii la dreapta: .

Si pentru STD se disting mai multe cazuri de calcul.

Sistem de tip SISO dat prin MM-II

Se da sistemul prin MM-II de forma:

a_ny(t)++ a₁y(t-n-1)+ a₀y(t-n)= b_mu(t)++ b₁u(t-m-1)+ b₀u(t-m)  (23)

Pentru calculul functiei de transfer, egalitatii (16) i se aplica transformata Z si se obtine:

a_ny(z)++ a₁^.z^-n+1.y(z)+ a₀^. z^-n.y(z)= b_m^.u(z)++ b₁^.z^-m+1.u(z)+ b₀^.z^-m. u(z).

Se aplica apoi definitia (16) si se obtine:

(24)

Sistem de tip MIMO dat prin MM-ISI

Se da un sistem de tip MIMO prin MM-ISI:

(25)

Formal, in conditii initiale nule avem:

(26)

Din ecuatia de stare din sistemul (26) rezulta:

Þ .

Se inlocuieste acest rezultat in ecuatia de iesire a sistemului (19) si se obtine:

.

Astfel, conform definitiei matricii de transfer se obtine:

(27)

Pentru sisteme de tip SISO, se obtine o functie de transfer de forma:

(28)

Trecerea formala contine in fond un ansamblu de calcule care constau in particularizarea relatiei de definitie a matricii de transfer pentru diversse valori ale lui t, inmultirea egalitatatilor cu puteri adecvate ale lui z, insumarea membru cu membru si recunoasterea in rezultate a transformatei Z a unei marimi.

Elemente de transfer tipizate

In aplicatiile practice exista anumite dependente functionale care apar cu o frecventa mai mare, intalnindu-se in modelarea a numeroase fenomene. Toate aceste cazuri au fost stranse sub denumirea de situatii si redate in anexa 3 .

In MM-II denumirea de: proportional, integrator, derivator, timp mort este data de membrul drept al modelului, unde apare marimea de intrare, iar denumirea de temporizare se asociaza ordinului derivare din membrul stang si caracterizeaza inertia elementului de transfer.

5. Stabilirea MM pentru conexiuni de sisteme

Daca se cunoaste structura unui sistem si MM ale subsistemelor componente, se poate detrmina MM al sistemului. Problema poate fi abordata atat in domeniul timp, cat si in domeniul operational.

In domeniul timp, rezolvarea apartine capitolului de eliminari din matematica. In concret, este vorba de a pastra marimea de intrare si de iesire daca se doreste un MM-II sau marimile de intrare, de stare si de iesire daca se doreste obtinerea unui MM-ISI si de a elimina restul marimilor. Mijloacele utilizate sunt substitutiile, reducerile artificiale matematice s.a.m.d.

In domeniul operational, calculul se bazeaza fie pe reconfigurarea schemelor bloc (algebra schemelor bloc) fie pe aplicarea asa-numitei formule a lui Mason. In primul caz este vorba despre interpretarea prin scheme bloc a formulelor de definire a matricilor si functiilor de transfer, iar in al doilea caz este vorba despre interpretarea prin functii de transfer a rezultatelor obtinute in cazul sistemelor liniare prin metode de calcul rezultate din regula lui Mason.

5.1. Calculul in domeniul timp

Se prezinta in continuare metodologia de calcul a MM-ISI al unui sistem cand se cunosc MM-ISI ale subsistemelor componente. Cazurile prezentate apar in mod frecvent in practica.

Se presupun cunoscute MM-ISI ale subsistemelor, si anume:

S1: si respectiv (29)

S2: (30)

Pentru subsistemele date se vor calcula in continuare MM-ISI ale sistemelor care le inglobeaza, in cazul a trei conexiuni de baza, si anume:

a) Conexiunea serie

Schema bloc corespunzatoare conexiunii serie este data in figura 5:

Figura 5

Este necesara completarea ecuatiilor (29) si (30) cu relatiile:

u₁=u , u₂=y₁ si y=y₂ (31)

care caracterizeaza conexiunea serie. Ecuatiile de stare ale conexiunii se obtin din ecuatiile de stare ale subsistemelor, retinand variabilele de stare si eliminand marimile intermediare. Se obtine astfel:

(32)

(33)

(34)

Sub forma matriciala, MM-ISI al sistemului este:

(35)

Rezultatul consemneaza, ca si in cazurile care urmeaza, faptul ca vectorul de stare al ansamblului se obtine prin agregarea vectorilor de stare ai subsistemelor componente.

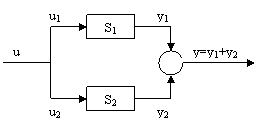
b) Conexiunea paralel

Structura conexiunii paralel este ilustrata in figura 6:

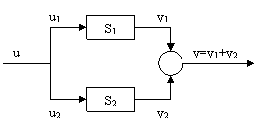
Figura 6

La ecuatiile (29) si (30) se mai adauga relatiile:

u₁=u₂=u si y=y₁+y₂ (36)

care caracterizeaza conexiunea paralel. Rezulta astfel dupa efectuarea calculelor, MM-ISI urmator:

(37)

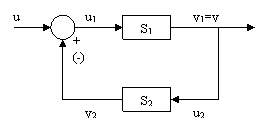
c) Conexiunea cu reactie

Se considera sistemele strict cauzale cu D₁=D₂=0. Figura 7 ilustreaza structura conexiunii cu reactie.

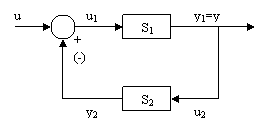
Figura 7

Ecuatiile (38) care caracterizeaza conexiunea cu reactie se adauga relatiilor (29) si (30):

u₁=u y si u₂=y₁=y (38)

Semnul '+' corespunde conexiunii cu reactie pozitiva, iar semnul '-' conexiunii cu reactie negativa. MM-ISI al sistemului, sub forma matriciala este urmatorul:

(39)

In cazurile concrete apar structuri mai mult sau mai putin complicate, principiul insa ramane acelasi: pornind de la relatiile ce caracterizeaza conexiunea, prin eliminari se obtine modelul ansamblului. Vectorii de stare agrega vectorii sistemelor componente.

5. Algebra schemelor bloc

In cadrul acestui procedeu, fiecare sistem este descris prin matricea de transfer H_i(l) pentru sistemele de tip MIMO sau prin functia de transfer pentru sistemele de tip SISO.

a) conexiunea serie

Pentru conexiunea serie se poate scrie, avand in vedere relatiile specifice conexiunii:

y(l)=y₂(l)=H₂(l)^.u₂(l)=H₂(l)^.y₁(l)=H₂(l)^.H₁(l)^.u₁(l)=H₂(l)^.H₁(l)^.u(l

Cum y(l)=H(l)^.u(l), din relatia anterioara rezulta ca:

H(l)=H₂(l)^.H₁(l (40)

Produsul (40) este comutativ doar in cazul sistemelor de tip SISO. Pentru conexiunea serie a unui numar de q sisteme este valabila relatia generala (41):

(41)

b) conexiunea paralel (derivatie)

In cazul conexiunii paralel se poate scrie, tinand cont de relatiile specifice:

H(l)=H₁(l)+H₂(l (42)

Suma (41) este comutativa atat in cazul sistemelor de tip SISO, cat si in cazul sistemelor de tip MIMO. In cazul general avem:

(43)

c) conexiunea cu reactie

Retinand din paragraful anterior relatiile specifice conexiunii cu reactie, se poate scrie:

y(l)=y₁(l)=H₁(l)^.u₁(l)=H₁(l)^.(u(l y l))=H₁(l)^.(u(l H l)^.u₂(l

Cum y(l)=u₂(l), rezulta din relatia anterioara ca:

Û

[I H₁(l)^.H₂(l)]^.y(l)=H₁(l)^.u(l) Þ

y(l)=[I H₁(l)^.H₂(l)]^-1.H₁(l)^.u(l), deci matricea de transfer a conexiunii

cu reactie este data de relatia (44):

H(l)=[I H₁(l)^.H₂(l)]^-1.H₁(l) (44)

Daca sistemele componenete sunt de tip SISO, matricea de transfer se reduce la o functie de transfer de forma:

(45)

Algebra schemelor bloc contine inafara celor trei cazuri prezentate si anumite reguli de compunere, permitand reconfigurarea schemelor bloc. Aceste reguli de compunere sunt prezentate in anexa 4.

6. Calculul raspunsului sistemelor liniare

Problema denumita in acest mod este problema detrminarii iesirii unui sistem atunci cand se cunosc modelul sistemului, intrarile sistemului si conditiile initiale. Din punct de vedere aplicativ distingem doua situatii:

calculul raspunsului in regim permanent;

calculul raspunsului in regim tranzitoriu.

Prima situatie poate fi obtinuta principial din cea de-a doua prin trecere la limita pentru t ¥. Cu toate acetea, dependentele de regim permanent pot fi obtinute si pe cale directa. Termenul 'aplicativ' are urmatorul inteles: de regula, un sistem realizat practic este destinat sa functioneze in regim permanent, iar daca sistemul este stabil atunci este capabil sa atinga un astfel de regim. Sistemele tehnice au de regula ca regim permanent regimul in care principalele marimi au valori nominale. Fata de acestea pot apare mici modificari, ca urmare a variatiei perturbatiilor de tip sarcina sau a marimii de conducere. Din punct de vedere aplicativ este important sa cunoastem cum se modifica in astfel de cazuri principalele marimi ale sistemului, sa observam daca exista o rezerva care sa permita pastrarea echilibrului sistemului inclusiv in prezenta acestor variatii, s.a.m.d.

In ceea ce priveste regimul tranzitoriu, intereseaza modul in care se face trecerea de la un regim permanent la alt regim permanent, respectiv calitatea acestui proces de trecere. Este important ca principalele marimi sa aiba variatii admisibile atat ca amplitudine, cat si ca durata.

6.1. Calculul raspunsului sistemelor liniare invariante in timp in regim tranzitoriu

Analitic, calculul se face pentru cazuri simple. In general, calculul se face doar numeric, pentru date bine precizate si are doar valabilitate locala. Pentru calculele numerice se pot utiliza mediile dedicate aplicatiilor sistemice (MATLAB, SIMULINK). Calculele numerice prezinta dezavantajul de a nu fi in mod simplu generalizabile, ele trebuie repetate, trebuie speculata orice observatie si dupa un numar mai mare sau mai mic de simulari se pot formula concluzii. Aceste concluzii au valoare doar de factura interpretativa si de sugerare a unor posibile dependente pentru alte situatii.

Calculele analitice au in contrast cu cele numerice, posibilitatea de a fi usor generalizabile, ele permit demonstratii in sens matematic. Din aceste motive au un grad de incredere mai ridicat. In mod obisnuit, aceste calcule nu se efectueaza in domeniul timp in mod direct, ci in domeniul operational. Daca conditiile initiale sunt nule, relatia de baza este urmatoarea:

y(l)=H(l)^.u(l (46)

iar pasii parcursi sunt urmatorii:

se determina H(l) pentru sistemul considerat;

se calculeaza u(l

cu relatia (46) se calculeaza y(l

se calculeaza din tabele y(t).

Daca conditiile initiale nu sunt nule, relatia (45) este inlocuita cu alte relatii, care prin particularizare conduc la formula (46). Astfel, pentru STC avem:

(47)

in care cu i=0,, n-1 sunt conditiile initiale ale marimii de iesire la momentul , iar cu i=0,, n-1 sunt conditiile initiale ale marimii de intrare la acelasi moment.

Expresiile pentru H_ui(s) si H_yi(s) sunt urmatoarele:

,

respectiv:

unde este polinomul caracteristic al sistemului.

Pentru STD avem:

in care y(-i) si u(-i) sunt conditiile initiale ale iesirii, respectiv intrarii. Expresiile pentru H_ui(z) si H_yi(z) sunt urmatoarele:

,

respectiv:

unde este polinomul caracteristic al sistemului.

Atunci cand dispunem de expresia operationala a unei functii de timp (evident asociata unei marimi dintr-un sistem) valoarea corespunzatoare la momentul t=0₊ () se poate obtine utilizand teorema valorii initiale. Astfel:

pentru STC, respectiv:

pentru STD.

7. Caracterizarea sistemelor in domeniul pulsatiilor

7.1. Definirea caracteristicilor de pulsatie pentru STC

Fie S un sistem cu orientarea de la u y. Presupunem ca la intrare se aplica o functie sinusoidala:

u(t)=u₀^.sin(w t)  (48)

In regim permanent sinusoidal (armonic) la iesire se obtine tot un raspuns sinusoidal, de forma:

y(t)=y^.sin(w t+j) (49)

Imaginam doua categorii de experimente:

Prima categorie de experimente se efectueaza la w=constant si se modifica doar amplitudinea semnalului de intrare u₀. Se constata ca in regim permanent constant se modifica amplitudinea semnalului de iesire y₀, iar defazajul j ramane constant. Mai mult, se constata ca raportul ramane de asemenea constant.

Cea de-a doua categorie de experimente pastreaza constanta amplitudinea semnalului de intrare u₀ si se modifica pulsatia w. Se constata ca de aceasta data se modifica atat amplitudinea semnalului de iesire y₀, cat si defazajul j

Rezultatele celor doua categorii de experimente pot caracterizate prin introducerea a doua functii de pulsatie:

(50)

(51)

Observatie: Pentru ca experimentele sa fie posibile, sistemul S s-a considerat ca fiind stabil, adica are capacitatea de a trece dintr-un regim permanent in alt regim permanent.

Presupunem ca sistemul S este liniar si ca functia lui de transfer este H(s). Se numeste functie de raspuns la pulsatie particularizarea lui H(s) pentru s=j^.w, adica functia:

, (52)

unde w este un numar real. Numarul H(j^.w) este un numar complex, deci poate fi scris sub forma:

(53)

Se poate demonstra ca:

(54)

(55)

Rezultatul obtinut este de importanta fundamentala, intrucat face legatura directa intre experiment si teorie. Ansamblul functiilor f₁ si f₂ poarta numele de caracteristici de pulsatie. Aceste caracteristuici se obtin de regula experimental. Pe de alta parte, pe baza relatiilor (54) si (55) caracteristicile de pulsatie se pot obtine si teoretic pornind de la functia de transfer. Importanta rezultatului consta in faptul ca teoretic au fost elaborate o seama de metode de analiza si sinteza a sistemelor bazate pe functia de raspuns la pulsatie, iar rezultatele pot fi aplicate direct unor caracteristici experimentale. In acest mod, in anumite situatii se poate ocoli operatia de modelare in domeniul timp.

In mod obisnuit, in locul caracteristicilor de pulsatie definite de relatiile (54) si (55) se utilizeaza carecteristici logaritmice si semilogaritmice de pulsatie, cunoscute sub denumirea de caracteristici Bode. In acest caz, variabila este logaritmul in baza 10 al pulsatiei. Notam:

w_lg = lg w (56)

In aceste conditii modulul functiei de raspuns la pulsatie se exprima in decibeli. Prima caracteristica este caracteristica amplitudine-pulsatie (c.a.p.):

, cu w>0  (57)

A doua caracteristica este caracteristica faza-pulsatie (c.f.p.):

, cu w>0  (58)

Relatiei (56) ii corespunde asa-numita axa logaritmica, aceasta fiind impartita dupa valorile logaritmului. Pe axa se noteaza valorile cantitatii logaritmate.

Unitatea pe axa logaritmica este decada. Ea reprezinta intervalul care desparte doua pulsatii aflate in intervalul 1 10. In figura 8 se prezinta doua aluri de principiu pentru caracteristicile Bode (s-a luat ca exemplu un sistem de ordinul al doilea):

Figura 8

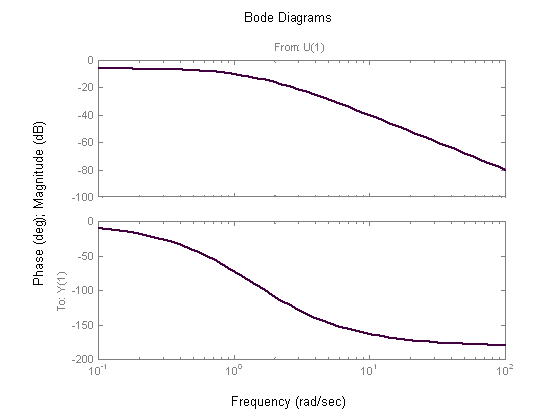
Caracteristicile de pulsatie se pot utiliza in multiple scopuri. Doua dintre acestea sunt:

Caracterizarea locala a sistemului face posibil calculul modulului si defazajului in situatiile in care pulsatia ia valori particulare, dupa formulele (57) si (58), (54) si (55), respectiv (49).

Caracterizarea globala a sistemului este data de ansamblul caracteristicilor si vizeaza inertia sistemului (capacitatea de a raspunde rapid sau lent la variatiile semnalului de intrare), stabilitatea sistemului si alte proprietati. De regula, din punct de vedere tehnic, inertia se ascunde sub alte denumiri.Acesta este cazul frecvent al filtrelor de semnal. Legat de caracterul inertial este valabila urmatoarea constatare: cu cat zona in care modulul functiei de raspuns la pulsatie (considerat in decibeli) este pozitiv se situeaza la pulsatii mai mari, cu atat viteza de raspuns a sistemului este mai mare. Din punct de vedere calitativ este velabila si urmatoarea corelatie: domeniul pulsatiilor mici ala caracteristicilor de pulsatie este corelabil cu regimul stationar constant, domeniul pulsatiilor mari cu inceputul regimului tranzitoriu, iar domeniul pulsatiilor medii cu portiunea mediana a regimului tranzitoriu.

Una din notiunile importante legate de caracterizarea sistemelor in domeniul pulsatiilor este notiunea de pulsatie de frangere. In figura 8 se observa ca la un moment dat caracteristica amplitudine-pulsatie se frange. Din acest motiv, w se numeste pulsatie de frangere. Pulsatia de frangere are urmatoarea relatie de calcul:

, (59)

unde T este constanta de timp a elementului de transfer a carui c.a.p. se reprezinta. Aceasta pulsatie este deci specifica fiecarui ET in parte.

O alta notiune care se defineste vis-à-vis de caracterizarea sistemelor in frecventa este rezerva de faza. In cazul in care se utilizeaza caracteristicile Bode, se defineste notiunea de rezerva de faza astfel:

, (60)

unde w_t reprezinta pulsatia de taiere a sistemului.

7. Aspecte tehnice referitoare la STC relevate cu ajutorul caracteristicilor de pulsatie

Domeniul de reprezentare al caracteristicilor de pulsatie se adopta in functie de domeniul spectral al semnalelor de intrare. In mod obisnuit, semnalele de intrare nu sunt sinusoidale, astfel incat ele au un domeniu spectral extins. Din punct de vedere practic vorbim despre semnale utile si semnale perturbatoare. Domeniul spectral al semnalelor utile este amplasat la pulsatii mai joase, iar domeniul spectral al semnalelor perturbatoare la pulsatii joase pentru perturbatii de tip sarcina si la pulsatii ridicate pentru perturbatii parazite. Pentru o aplicatie concreta, punctul de plecare in stabilirea domeniului de reprezentare il constituie informatiile apriorice referitoare la semnalul de intrare si componentele acestuia.

Inertia unui sistem poate fi asociata cu frangerile si pulsatiile la care au loc aceste frangeri. Practic, pentru orice sistem fizic care este evident un sistem inertial, caracteristicile de pulsatie ar trebui sa aiba pentru pulsatii mari o alura descrescatoare cu o panta de -20 dB/decada sau multiplu al acesteia si un defazaj de -p/2 radiani sau multiplu al acestuia.

Datorita domeniului limitat de pulsatii pe care se face reprezentarea este posibil ca aceasta sa nu surprinda caracterul inertial in mod complet. In astfel de situatii este posibil sa simplificam modelul matematic al sistemului pentru care se face reprezentarea.

7.3. Definirea caracteristicilor de pulsatie pentru STD

In cazul STD caracteristicile de pulsatie se utilizeaza in special in domeniul prelucrarii semnalelor si mai putin in domeniul conducerii proceselor.

Fie un STD cu functia de transfer H(z). Se numeste functie de raspuns la pulsatie in timp discret particularizarea lui H(z) pentru situatia cand z parcurge cercul de raza unitate.

, , (61)

unde I reprezinta un interval de lungime 2p pe care functia e^jwh este periodica.

Ca si in cazul STC legatura cu partea experimentala este redata de urmatoarea situatie. Fie un semnal in timp discret care rezulta prin esantionare cu pasul h dintr-un semnal sinusoidal in timp continuude pulsatie w, adica:

u(k)=u₀^.sin(w t) , pentru t=k^.h , adica

u(k)=u₀^.sin(w k^.h) , unde kIZ (62)

Aplicand acest semnal la intarea sistemului cu functia de transfer H(z), la iesire se obtine semnalul:

y(k)=, cu kIZ 

Se observa ca lucrurile se petrec in principiu la fel ca in cazul STC. Pe aceasta baza se introduc caracteristicile de pulsatie ale STD astfel. Caracteristica amplitudine-pulsatie este data de:

(64)

iar caracteristica faza-pulsatie este data de:

(65)

In ambele reprezentari w hII.

Spre deosebire de STC, pentru reprezentarea caracteristicilor de pulsatie pentru STD nu se mai utilizeaza axe logaritmice.